江苏省常州市新北区实验学校苏科版八年级数学上册 1.3 探索三角形全等的条件8 (共12张PPT)
文档属性
| 名称 | 江苏省常州市新北区实验学校苏科版八年级数学上册 1.3 探索三角形全等的条件8 (共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 334.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-07 00:00:00 | ||
图片预览



文档简介
课件12张PPT。
1.3 探索三角形全等的条件8
——两个直角三角形全等的判定
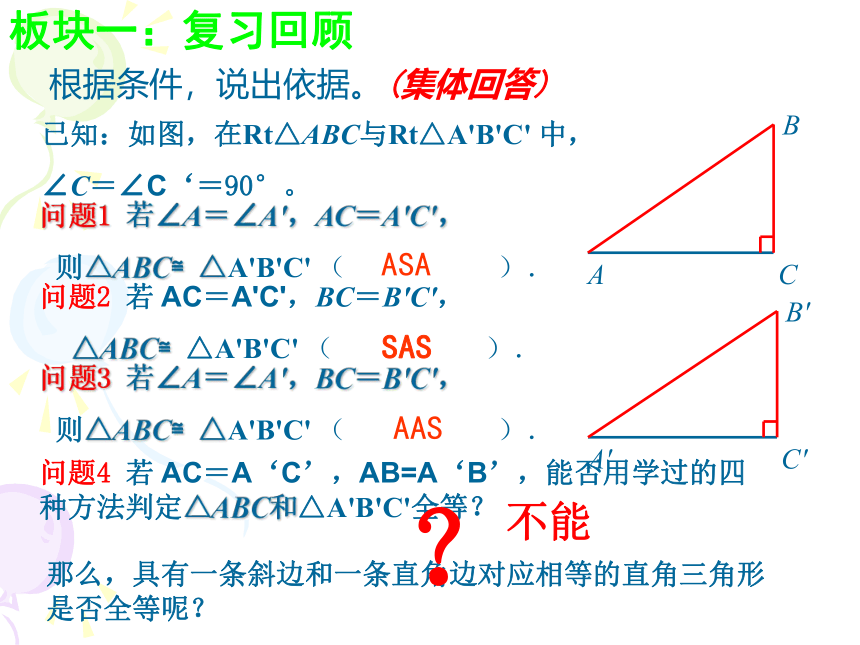
根据条件,说出依据。(集体回答)已知:如图,在Rt△ABC与Rt△A'B'C' 中,
∠C=∠C‘=90°。问题1 若∠A=∠A',AC=A'C',
则△ABC≌△A'B'C' ( ).ASASAS问题2 若 AC=A'C',BC=B'C',
△ABC≌△A'B'C' ( ).问题3 若∠A=∠A',BC=B'C',
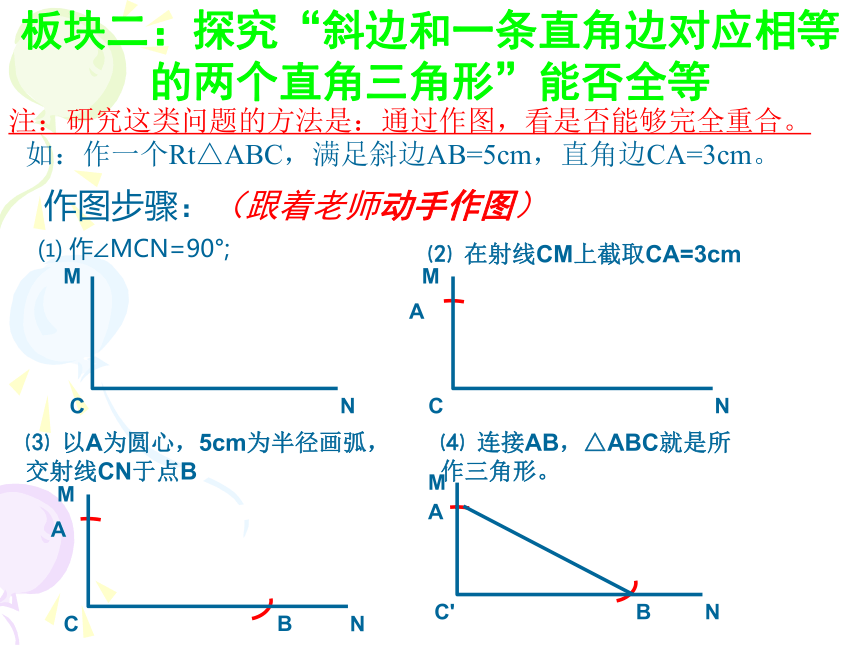
则△ABC≌△A'B'C' ( ).AAS问题4 若 AC=A‘C’,AB=A‘B’,能否用学过的四种方法判定△ABC和△A'B'C'全等?不能板块一:复习回顾那么,具有一条斜边和一条直角边对应相等的直角三角形是否全等呢??板块二:探究“斜边和一条直角边对应相等的两个直角三角形”能否全等注:研究这类问题的方法是:通过作图,看是否能够完全重合。如:作一个Rt△ABC,满足斜边AB=5cm,直角边CA=3cm。 作图步骤:(跟着老师动手作图)问题1 你与同伴所作的两个直角三角形能重合吗?(同伴合作)问题2 请你描述一下你所发现的结论?
(同伴交流)探索发现的规律是:斜边、直角边定理 斜边和一条直角边对应相等的两个直角三角形全等.前提条件1条件2简写成“斜边、直角边”或“HL”∴在Rt△ABC和Rt△A′B′C′中,几何语言: ∵ ∠C=∠C′ =90°(HL)BC=B′C′RtRtRtRtABCDABCD问题4 已知:如图, △ABC中,AB=AC,
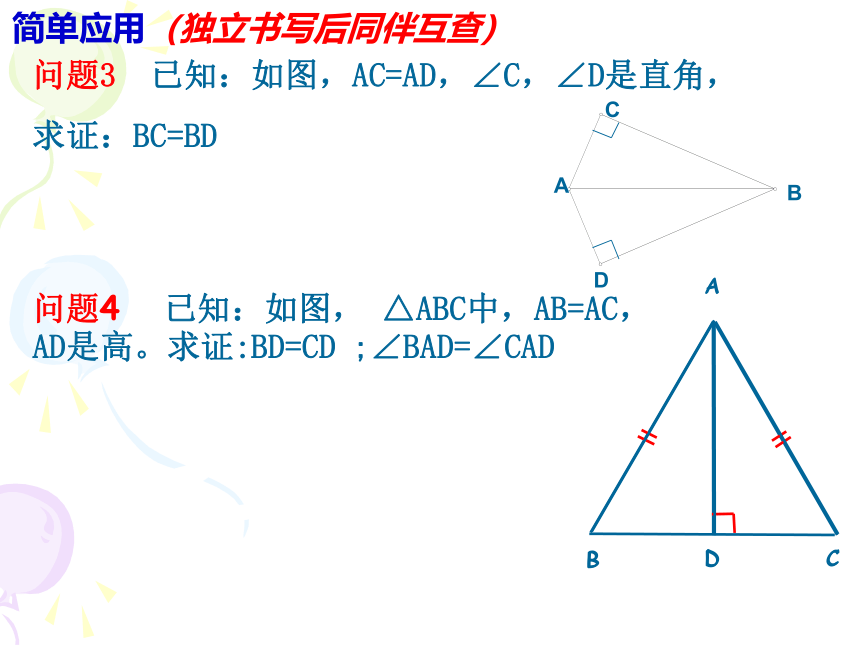
AD是高。求证:BD=CD ;∠BAD=∠CAD问题3 已知:如图,AC=AD,∠C,∠D是直角,
求证:BC=BD简单应用(独立书写后同伴互查)例题:如图,AB=DC,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.(倾听)分析:1、审题:① AE⊥BC, DF⊥BC
∠AEB=∠DFC=90°(直角)板块三:“HL”定理的应用2、审图:CE-EF=BF-EF(直角边)。3、审结论:需证明Rt⊿ABE≌ Rt⊿DCF HL(独立书写证明过程)② AB= DC(斜边);③CE=BF(与直角边相关)。审题三步骤阅读材料 如图1,E、F分别为线段AC上的两个
动点,且DE⊥AC于E点,BF⊥AC于F点,若
AB=CD,AF=CE,BD交AC于M点。问题2 当E、F两点移动至图2所示的位置时,其
余条件不变,上述结论是否成立?若成立,
给予证明。(独立思考后与同伴交流)问题1 求证:MB=MD,ME=MF;
(独立完成后同伴互查)
板块四:灵活应用问题1 判断下列判断正确吗,并说明理由:
(独立思考后同伴交流)③两直角边对应相等的两个直角三角形全等;④一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.×√√①两个锐角对应相等的两个直角三角形全等; ②斜边及一个锐角对应相等的两个直角三角形全等;√1.AB=DC (HL)
2.AC=DB (HL)
3.∠ABC=∠DCB (AAS)
4.∠ACB=∠DBC (AAS)
…… 问题3 有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,问P点运动到AC上什么位置时,△ABC才能和△APQ全等?
(同伴交流)收获:“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等一般三角形与直角三角形全等的判定方法的比较:
(倾听并归纳)
1.3 探索三角形全等的条件8
——两个直角三角形全等的判定
根据条件,说出依据。(集体回答)已知:如图,在Rt△ABC与Rt△A'B'C' 中,
∠C=∠C‘=90°。问题1 若∠A=∠A',AC=A'C',
则△ABC≌△A'B'C' ( ).ASASAS问题2 若 AC=A'C',BC=B'C',
△ABC≌△A'B'C' ( ).问题3 若∠A=∠A',BC=B'C',
则△ABC≌△A'B'C' ( ).AAS问题4 若 AC=A‘C’,AB=A‘B’,能否用学过的四种方法判定△ABC和△A'B'C'全等?不能板块一:复习回顾那么,具有一条斜边和一条直角边对应相等的直角三角形是否全等呢??板块二:探究“斜边和一条直角边对应相等的两个直角三角形”能否全等注:研究这类问题的方法是:通过作图,看是否能够完全重合。如:作一个Rt△ABC,满足斜边AB=5cm,直角边CA=3cm。 作图步骤:(跟着老师动手作图)问题1 你与同伴所作的两个直角三角形能重合吗?(同伴合作)问题2 请你描述一下你所发现的结论?
(同伴交流)探索发现的规律是:斜边、直角边定理 斜边和一条直角边对应相等的两个直角三角形全等.前提条件1条件2简写成“斜边、直角边”或“HL”∴在Rt△ABC和Rt△A′B′C′中,几何语言: ∵ ∠C=∠C′ =90°(HL)BC=B′C′RtRtRtRtABCDABCD问题4 已知:如图, △ABC中,AB=AC,
AD是高。求证:BD=CD ;∠BAD=∠CAD问题3 已知:如图,AC=AD,∠C,∠D是直角,
求证:BC=BD简单应用(独立书写后同伴互查)例题:如图,AB=DC,AE ⊥BC,DF ⊥BC,
CE=BF. 求证:AE=DF.(倾听)分析:1、审题:① AE⊥BC, DF⊥BC
∠AEB=∠DFC=90°(直角)板块三:“HL”定理的应用2、审图:CE-EF=BF-EF(直角边)。3、审结论:需证明Rt⊿ABE≌ Rt⊿DCF HL(独立书写证明过程)② AB= DC(斜边);③CE=BF(与直角边相关)。审题三步骤阅读材料 如图1,E、F分别为线段AC上的两个
动点,且DE⊥AC于E点,BF⊥AC于F点,若
AB=CD,AF=CE,BD交AC于M点。问题2 当E、F两点移动至图2所示的位置时,其
余条件不变,上述结论是否成立?若成立,
给予证明。(独立思考后与同伴交流)问题1 求证:MB=MD,ME=MF;
(独立完成后同伴互查)
板块四:灵活应用问题1 判断下列判断正确吗,并说明理由:
(独立思考后同伴交流)③两直角边对应相等的两个直角三角形全等;④一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.×√√①两个锐角对应相等的两个直角三角形全等; ②斜边及一个锐角对应相等的两个直角三角形全等;√1.AB=DC (HL)
2.AC=DB (HL)
3.∠ABC=∠DCB (AAS)
4.∠ACB=∠DBC (AAS)
…… 问题3 有一Rt△ABC,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AM上运动,问P点运动到AC上什么位置时,△ABC才能和△APQ全等?
(同伴交流)收获:“SAS”“ ASA ”“ AAS ”“ SSS ”“ SAS ”“ ASA ”“ AAS ”“ HL ”灵活运用各种方法证明直角三角形全等一般三角形与直角三角形全等的判定方法的比较:
(倾听并归纳)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
