吉林省长春市第十一高中等三校2024-2025学年高一上学期第三学程数学考试卷(含答案)
文档属性
| 名称 | 吉林省长春市第十一高中等三校2024-2025学年高一上学期第三学程数学考试卷(含答案) | 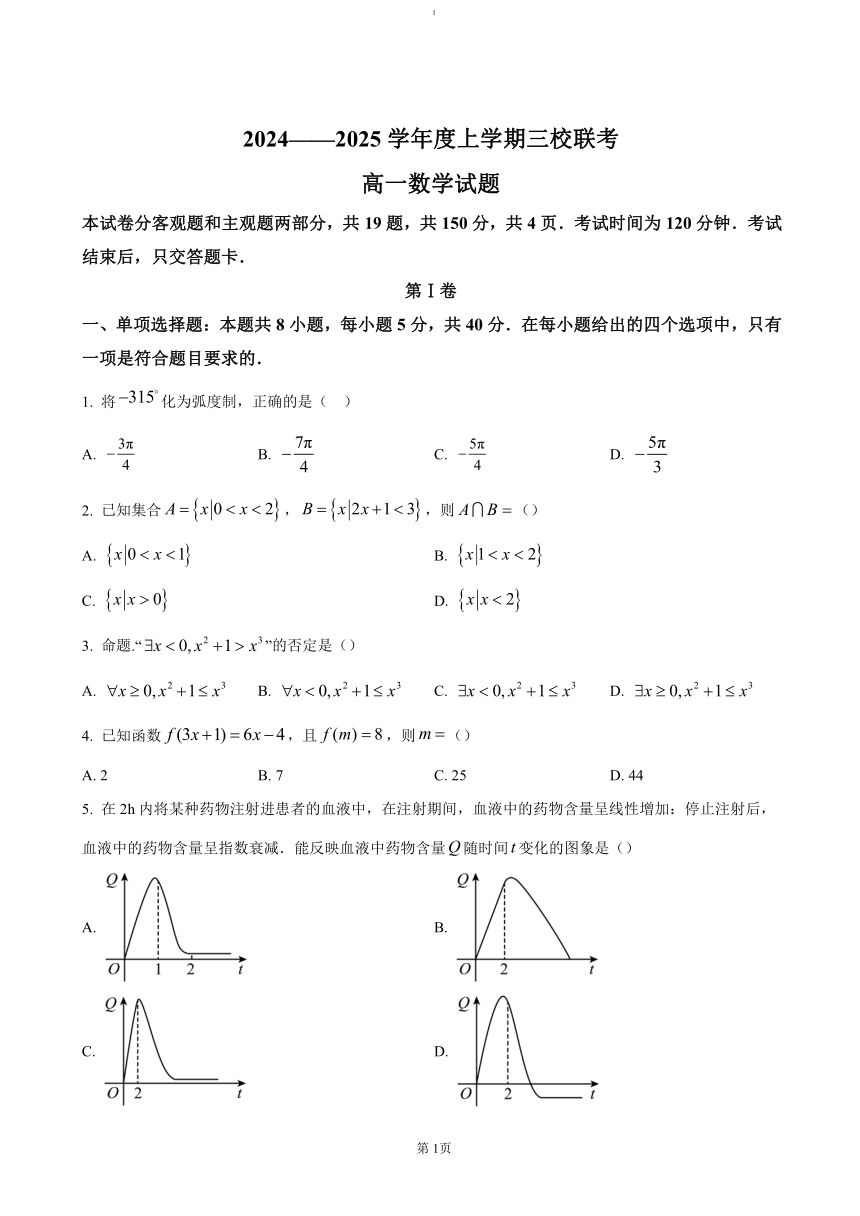 | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 12:38:43 | ||
图片预览





文档简介
1
2024——2025学年度上学期三校联考
高一数学试题
本试卷分客观题和主观题两部分,共19题,共150分,共4页.考试时间为120分钟.考试结束后,只交答题卡.
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 将化为弧度制,正确的是( )
A. B. C. D.
2. 已知集合,,则()
A. B.
C. D.
3. 命题.“”的否定是()
A. B. C. D.
4. 已知函数,且,则()
A. 2 B. 7 C. 25 D. 44
5. 在2h内将某种药物注射进患者的血液中,在注射期间,血液中的药物含量呈线性增加:停止注射后,血液中的药物含量呈指数衰减.能反映血液中药物含量随时间变化的图象是()
A. B.
C. D.
6. 已知函数的值域为,则实数的取值范围是()
A. B. C. D.
7. 已知函数为定义在R上的奇函数,且在上单调递减,满足,则实数a的取值范围为()
A. B. C. D.
8. 已知,,若关于的不等式在上恒成立,则的最小值是()
A4 B. C. 8 D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的是( )
A. 关于x的不等式的解集为,则不等式的解集为
B. 若函数定义域是,则函数的定义域是
C. 函数的单调递增区间为
D. 已知实数a,b满足,,则3a + b的取值范围是
10. 定义,设,则()
A. 有最大值,无最小值
B. 当的最大值为
C. 不等式的解集为
D. 的单调递增区间为
11. 已知,则下列结论正确的是()
A B. C. D.
第Ⅱ卷
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知,若关于的方程有两个不等的实数根,则实数的取值范围是__________.
13. 已知幂函数图象过点,若,则实数的取值范围是________.
14. 若正实数满足,不等式有解,则的取值范围是____________.
四、解答题
15. 对于集合A,B,我们把集合记作.例如,,;则有,,,,
据此,试回答下列问题.
(1)已知,,求;
(2)已知,求集合A,B;
(3)A有3个元素,B有4个元素,试确定有几个元素.
16. 已知是定义在[-4,4]上的奇函数,当时,.
(1)求在[,0)上的解析式;
(2)若存在,使得不等式成立,求m的取值范围.
17. 某企业生产,两种产品,根据市场调查和预测,产品的利润(万元)与投资额(万元)成正比,其关系如图(1)所示;产品的利润(万元)与投资额(万元)的算术平方根成正比,其关系如图(2)所示.
(1)分别将,两种产品的利润表示为投资额的函数;
(2)该企业已筹集到10万元资金,并全部投入,两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润?其最大利润约为多少万元(精确到1万元)?
18. 已知函数,关于的不等式的解集为,且.
(1)求的值;
(2)是否存在实数,使函数的最小值为?若存在,求出的值;若不存在,说明理由.
19. 取名于荷兰数学家鲁伊兹·布劳威尔不动点定理是拓扑学里一个非常重要的定理.该定理表明:对于满足一定条件的图象连续不间断的函数,在其定义域内存在一点,使得,则称为函数的一个“不动点”.若,则称为的“稳定点”.将函数的“不动点”和“稳定点”的集合分别记为A和B,即,,.已知函数.
(1)当,时,求函数不动点;
(2)若对于任意,函数恒有两个相异的不动点,求实数m的取值范围;
(3)若时,且,求实数n的取值范围.
2024——2025学年度上学期三校联考
高一数学试题
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】B
2.
【答案】A
3.
【答案】B
4.
【答案】B
5.
【答案】C
6.
【答案】B
7.
【答案】D
8.
【答案】C
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.
【答案】ABD
10.
【答案】BC
11.
【答案】ABD
第Ⅱ卷
三、填空题:本题共3小题,每小题5分,共15分.
12.
【答案】
13.
【答案】
14.
【答案】
四、解答题
15.
【解析】
【分析】根据的定义求解即可.
【小问1详解】
因为,,根据已知有:.
【小问2详解】
因为,所以.
【小问3详解】
从以上解题过程中可以看出,中元素的个数与集合和集合中的元素个数有关,
即集合中的任何一个元素与集合中的一个元素对应后,得到中的一个新元素.
若集合中有个元素,集合中有个元素,则中有个元素,
故有个元素,B有个元素,中有个元素.
16.
【解析】
【分析】(1)根据奇函数的定义求解析式;
(2)不等式用分离参数法变形,转化为求函数的最值,然后得参数范围.
【小问1详解】
当时,,所以,
又,所以,
所以在[,0)上的解析式为;
【小问2详解】
由(1)知,时,,
所以可整理得,
令,根据指数函数单调性可得,为减函数,
因为存在,使得不等式成立,等价于在上有解,
所以,只需,
所以实数m的取值范围是.
17.
【解析】
【分析】(1)由已知给出的函数模型设出解析式,代入已知数据即可算出结果;
(2)设产品投入万元,则产品投入万元,设企业的利润为万元,则有,再利用换元法转化为求二次函数在给定区间上的最值问题即可求解.
【小问1详解】
设投资额为万元,产品的利润为万元,产品的利润为万元,
由题设,,
由图可知(1),所以,又(4),所以,
所以,;
【小问2详解】
设产品投入万元,则产品投入万元,设企业的利润为万元,
,,
令,则,,
所以当时,,此时,
所以当产品投入3.75万元,产品投入6.25万元,企业获得最大利润为万元,约为4万元.
18.
【解析】
【分析】(1)先根据,求出不等式的解,结合可得的值;
(2)利用换元法,把函数转化为二次函数,结合二次函数区间最值法求解.
小问1详解】
由可得,又,所以,
又因为的解集为,所以,
因为,所以,即,
解得或,因为,所以;
【小问2详解】
由(1)可得,
令,则,设,
①当时,在上单调递增,
则,解得,符合要求;
②当时,在上单调递减,在上单调递增,
,解得,又,故;
③当时,在上单调递减,
,解得,不合题意;
综上所述,存在实数或符合题意.
19.
【解析】
【分析】(1)求出方程的解后可得不动点;
(2)根据的判别式恒正可得关于恒成立的不等式,结合可求的取值范围;
(3)记,则即无解或其解为,故可求的取值范围.
【小问1详解】
当,时,,
设为不动点,因此,解得或,
所以为函数的不动点;
【小问2详解】
因为恒有两个不动点,
即恒有两个不等实根,
整理为,
所以且恒成立,
令,
所以,所以,
解得或,又,
所以;
【小问3详解】
时,,
因为,所以有实根,
所以,即,
记,则关于的方程的解为方程组的解的值,
两式相减可得,
因为,即要使与有相同的解,
则与的的解集相同,
所以方程无解或其解为,
所以,即,
综上,所以实数n的取值范围是.
PAGE
第6页
2024——2025学年度上学期三校联考
高一数学试题
本试卷分客观题和主观题两部分,共19题,共150分,共4页.考试时间为120分钟.考试结束后,只交答题卡.
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 将化为弧度制,正确的是( )
A. B. C. D.
2. 已知集合,,则()
A. B.
C. D.
3. 命题.“”的否定是()
A. B. C. D.
4. 已知函数,且,则()
A. 2 B. 7 C. 25 D. 44
5. 在2h内将某种药物注射进患者的血液中,在注射期间,血液中的药物含量呈线性增加:停止注射后,血液中的药物含量呈指数衰减.能反映血液中药物含量随时间变化的图象是()
A. B.
C. D.
6. 已知函数的值域为,则实数的取值范围是()
A. B. C. D.
7. 已知函数为定义在R上的奇函数,且在上单调递减,满足,则实数a的取值范围为()
A. B. C. D.
8. 已知,,若关于的不等式在上恒成立,则的最小值是()
A4 B. C. 8 D.
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的是( )
A. 关于x的不等式的解集为,则不等式的解集为
B. 若函数定义域是,则函数的定义域是
C. 函数的单调递增区间为
D. 已知实数a,b满足,,则3a + b的取值范围是
10. 定义,设,则()
A. 有最大值,无最小值
B. 当的最大值为
C. 不等式的解集为
D. 的单调递增区间为
11. 已知,则下列结论正确的是()
A B. C. D.
第Ⅱ卷
三、填空题:本题共3小题,每小题5分,共15分.
12. 已知,若关于的方程有两个不等的实数根,则实数的取值范围是__________.
13. 已知幂函数图象过点,若,则实数的取值范围是________.
14. 若正实数满足,不等式有解,则的取值范围是____________.
四、解答题
15. 对于集合A,B,我们把集合记作.例如,,;则有,,,,
据此,试回答下列问题.
(1)已知,,求;
(2)已知,求集合A,B;
(3)A有3个元素,B有4个元素,试确定有几个元素.
16. 已知是定义在[-4,4]上的奇函数,当时,.
(1)求在[,0)上的解析式;
(2)若存在,使得不等式成立,求m的取值范围.
17. 某企业生产,两种产品,根据市场调查和预测,产品的利润(万元)与投资额(万元)成正比,其关系如图(1)所示;产品的利润(万元)与投资额(万元)的算术平方根成正比,其关系如图(2)所示.
(1)分别将,两种产品的利润表示为投资额的函数;
(2)该企业已筹集到10万元资金,并全部投入,两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润?其最大利润约为多少万元(精确到1万元)?
18. 已知函数,关于的不等式的解集为,且.
(1)求的值;
(2)是否存在实数,使函数的最小值为?若存在,求出的值;若不存在,说明理由.
19. 取名于荷兰数学家鲁伊兹·布劳威尔不动点定理是拓扑学里一个非常重要的定理.该定理表明:对于满足一定条件的图象连续不间断的函数,在其定义域内存在一点,使得,则称为函数的一个“不动点”.若,则称为的“稳定点”.将函数的“不动点”和“稳定点”的集合分别记为A和B,即,,.已知函数.
(1)当,时,求函数不动点;
(2)若对于任意,函数恒有两个相异的不动点,求实数m的取值范围;
(3)若时,且,求实数n的取值范围.
2024——2025学年度上学期三校联考
高一数学试题
第Ⅰ卷
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
【答案】B
2.
【答案】A
3.
【答案】B
4.
【答案】B
5.
【答案】C
6.
【答案】B
7.
【答案】D
8.
【答案】C
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.
【答案】ABD
10.
【答案】BC
11.
【答案】ABD
第Ⅱ卷
三、填空题:本题共3小题,每小题5分,共15分.
12.
【答案】
13.
【答案】
14.
【答案】
四、解答题
15.
【解析】
【分析】根据的定义求解即可.
【小问1详解】
因为,,根据已知有:.
【小问2详解】
因为,所以.
【小问3详解】
从以上解题过程中可以看出,中元素的个数与集合和集合中的元素个数有关,
即集合中的任何一个元素与集合中的一个元素对应后,得到中的一个新元素.
若集合中有个元素,集合中有个元素,则中有个元素,
故有个元素,B有个元素,中有个元素.
16.
【解析】
【分析】(1)根据奇函数的定义求解析式;
(2)不等式用分离参数法变形,转化为求函数的最值,然后得参数范围.
【小问1详解】
当时,,所以,
又,所以,
所以在[,0)上的解析式为;
【小问2详解】
由(1)知,时,,
所以可整理得,
令,根据指数函数单调性可得,为减函数,
因为存在,使得不等式成立,等价于在上有解,
所以,只需,
所以实数m的取值范围是.
17.
【解析】
【分析】(1)由已知给出的函数模型设出解析式,代入已知数据即可算出结果;
(2)设产品投入万元,则产品投入万元,设企业的利润为万元,则有,再利用换元法转化为求二次函数在给定区间上的最值问题即可求解.
【小问1详解】
设投资额为万元,产品的利润为万元,产品的利润为万元,
由题设,,
由图可知(1),所以,又(4),所以,
所以,;
【小问2详解】
设产品投入万元,则产品投入万元,设企业的利润为万元,
,,
令,则,,
所以当时,,此时,
所以当产品投入3.75万元,产品投入6.25万元,企业获得最大利润为万元,约为4万元.
18.
【解析】
【分析】(1)先根据,求出不等式的解,结合可得的值;
(2)利用换元法,把函数转化为二次函数,结合二次函数区间最值法求解.
小问1详解】
由可得,又,所以,
又因为的解集为,所以,
因为,所以,即,
解得或,因为,所以;
【小问2详解】
由(1)可得,
令,则,设,
①当时,在上单调递增,
则,解得,符合要求;
②当时,在上单调递减,在上单调递增,
,解得,又,故;
③当时,在上单调递减,
,解得,不合题意;
综上所述,存在实数或符合题意.
19.
【解析】
【分析】(1)求出方程的解后可得不动点;
(2)根据的判别式恒正可得关于恒成立的不等式,结合可求的取值范围;
(3)记,则即无解或其解为,故可求的取值范围.
【小问1详解】
当,时,,
设为不动点,因此,解得或,
所以为函数的不动点;
【小问2详解】
因为恒有两个不动点,
即恒有两个不等实根,
整理为,
所以且恒成立,
令,
所以,所以,
解得或,又,
所以;
【小问3详解】
时,,
因为,所以有实根,
所以,即,
记,则关于的方程的解为方程组的解的值,
两式相减可得,
因为,即要使与有相同的解,
则与的的解集相同,
所以方程无解或其解为,
所以,即,
综上,所以实数n的取值范围是.
PAGE
第6页
同课章节目录
