湖南省宁远县第一中学2015-2016学年高一下学期第一次月考数学试题
文档属性
| 名称 | 湖南省宁远县第一中学2015-2016学年高一下学期第一次月考数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 220.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-05 00:00:00 | ||
图片预览




文档简介
宁远一中2016年上期高一年级第一次月考数学科目试题卷
命题人:欧致富 审题人:欧阳才学
1.本卷共22题,满分150分,考试时间为120分钟。
2.考生领取到试卷后,应检查试卷是否有缺页漏页,重影模糊等妨碍答题现象,如有请立即向监考老师通报。
一.选择题(每题5分,共50分。在每题后面所给的四个选项中,只有一个是正确的。)
1.的值等于( )
A.. B. C. D.
2.设,那么( )
A.B. C. D.
3.已知,则
A.. B. C. D.
A.
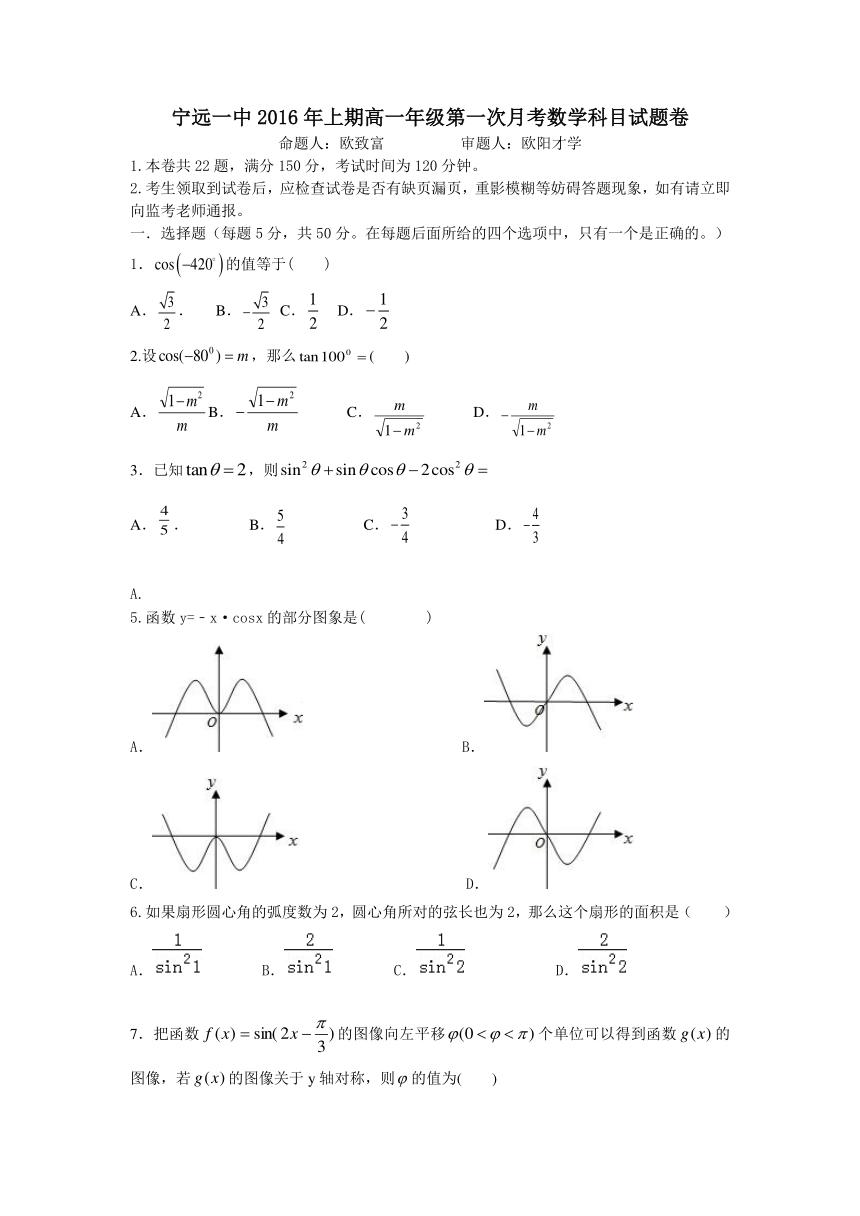
5.函数y=﹣x·cosx的部分图象是( )
A. B.
C. D.
6.如果扇形圆心角的弧度数为2,圆心角所对的弦长也为2,那么这个扇形的面积是( )
A. B. C. D.
7.把函数的图像向左平移个单位可以得到函数的图像,若的图像关于y轴对称,则的值为( )
A. B. C.或 D.
8.已知函数(,,)在时取得最大值,且它的最小正周期为,则()
A.的图象过点 B.在上是减函数
C.的一个对称中心是 D.的图象的一条对称轴是
9.要得到函数的图像,可以将函数的图像( )
A.沿x轴向左平移个单位 B.沿x轴向右平移个单位
C.沿x轴向左平移个单位 D.沿x轴向右平移个单位
10. 如果函数 f(x)是定义在(-3 ( http: / / www.21cnjy.com ),3)上的奇函数,当0<x<3时,函数 f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是
A.∪(0,1)∪
B.∪(0,1)∪
C.(- 3,- 1)∪(0,1)∪(1,3)
D.∪(0,1)∪(1,3)
二.填空题(每题5分,共25分)
11.若,那么的值为
12.设为第四象限角,其终边上的一个点是P(x,-),且,则
_______.
13.若 cos(75°+α)=,其中α为第三象限角,则cos(105°-α)+sin(α-105°)= _______.
14.下面有5个命题:
①函数
2x的最小正周期是π.
②若为第二象限角则在一、三、四象限;
③在同一坐标系中,函数y=sin x的图象和函数y=x的图象有3个公共点.
④把函数y=3sin的图象向右平移得到y=3sin 2x的图象.
⑤函数y=sin在[0,π]上是减函数.
其中,真命题的编号是______.(写出所有真命题的编号)
15.函数是常数,且)的部分图象如图所示,下列结论:
①最小正周期为;
②将的图象向左平移个单位,所得到的函数是偶函数;
③;④;
⑤,其中正确的是_______.
三、解答题:(75分)
16.(本小题12分)化简下列各式:
(1);
(2),其中
17. (本小题12分)已知是第三象限角,且
(1)化简 (2)若求的值
(3)若求的值
18.(本小题12分)已知是关于的二次方程的两个实数根,求:(1)的值;(2)的值.
19.(本小题13分)已知函数的部分图象如图所示.
( http: / / www.21cnjy.com / )
(Ⅰ)求函数的解析式;
(Ⅱ)求函数的单调递增区间.
20.(本小题满分13分)已知函数
(1)用五点法在给定的坐标系中作出函数的一个周期的图象;
(2)求函数的单调区间;
(3)求此函数的图象的对称轴方程、对称中心.
( http: / / www.21cnjy.com / )
21.(本小题满分13分)某商品一年内出厂 ( http: / / www.21cnjy.com )价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试分别建立出厂价格、销售价格的模型,并分别求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数;
(3) 求该商店月利润的最大值.
宁远一中2016年上期高一年级第一次月考数学科目试题答案
1.本卷共22题,满分150分,考试时间为120分钟。
2.考生领取到试卷后,应检查试卷是否有缺页漏页,重影模糊等妨碍答题现象,如有请立即向监考老师通报。
一.选择题(每题5分,共50分。在每题后面所给的四个选项中,只有一个是正确的。)
1.的值等于( A )
A.. B. C. D.
2.设,那么( B )
A.B. C. D.
3.已知,则( D )
A.. B. C. D.
A.
5.函数y=﹣x·cosx的部分图象是( D )
A. B.
C. D.
6.如果扇形圆心角的弧度数为2,圆心角所对的弦长也为2,那么这个扇形的面积是( B )
A. B. C. D.
7.把函数的图像向左平移个单位可以得到函数的图像,若的图像关于y轴对称,则的值为( D )
A. B. C.或 D.
8.已知函数(,,)在时取得最大值,且它的最小正周期为,则( C )
A.的图象过点 B.在上是减函数
C.的一个对称中心是 D.的图象的一条对称轴是
9.要得到函数的图像,可以将函数的图像( A )
A.沿x轴向左平移个单位 B.沿x轴向右平移个单位
C.沿x轴向左平移个单位 D.沿x轴向右平移个单位
10. 如果函数 f(x)是定义在(-3, ( http: / / www.21cnjy.com )3)上的奇函数,当0<x<3时,函数 f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( B )
A.∪(0,1)∪
B.∪(0,1)∪
C.(- 3,- 1)∪(0,1)∪(1,3)
D.∪(0,1)∪(1,3)
二.填空题(每题5分,共25分)
11.若,那么的值为 --1
12.设为第四象限角,其终边上的一个点是P(x,-),且,则
_______.
13.若 cos(75°+α)=,其中α为第三象限角,则cos(105°-α)+sin(α-105°)= _______.
14.下面有5个命题:
①函数
2x的最小正周期是π.
②若为第二象限角则在一、三、四象限;
③在同一坐标系中,函数y=sin x的图象和函数y=x的图象有3个公共点.
④把函数y=3sin的图象向右平移得到y=3sin 2x的图象.
⑤函数y=sin在[0,π]上是减函数.
其中,真命题的编号是___①④____.(写出所有真命题的编号)
15.函数是常数,且)的部分图象如图所示,下列结论:
①最小正周期为;
②将的图象向左平移个单位,所得到的函数是偶函数;
③;④;
⑤,其中正确的是_①④⑤______.
三、解答题:(75分)
16.(本小题12分)化简下列各式:
(1);
(2),其中
解:(1)原式=-1
(2)原式=
17. (本小题12分)已知是第三象限角,且
(1)化简 (2)若求的值
(3)若求的值
解:(1) (2) (3)
18.(本小题12分)已知是关于的二次方程的两个实数根,求:(1)的值;(2)的值.
解:(1)
(2) 原式
19.(本小题13分)已知函数的部分图象如图所示.
( http: / / www.21cnjy.com / )
(Ⅰ)求函数的解析式;
(Ⅱ)求函数的单调递增区间.
解:(1)
(2)
20.(本小题满分13分)已知函数
(1)用五点法在给定的坐标系中作出函数的一个周期的图象;
(2)求函数的单调区间;
(3)求此函数的图象的对称轴方程、对称中心.
解:(1)略
(2)单调递增区间: 递减区间:
(3) 对称轴方程是:; 对称中心
21.(本小题满分13分) ( http: / / www.21cnjy.com )某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试分别建立出厂价格、销售价格的模型,并分别求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数;
(3) 求该商店月利润的最大值.
解:(1)设出厂价格关于月份的函数为:;
销售价格关于月份的函数为:
依题意得:,
(2) 设月利润函数为:
(3) 该商店月利润的最大值为:
(第10题)
(第10题)
命题人:欧致富 审题人:欧阳才学
1.本卷共22题,满分150分,考试时间为120分钟。
2.考生领取到试卷后,应检查试卷是否有缺页漏页,重影模糊等妨碍答题现象,如有请立即向监考老师通报。
一.选择题(每题5分,共50分。在每题后面所给的四个选项中,只有一个是正确的。)
1.的值等于( )
A.. B. C. D.
2.设,那么( )
A.B. C. D.
3.已知,则
A.. B. C. D.
A.
5.函数y=﹣x·cosx的部分图象是( )
A. B.
C. D.
6.如果扇形圆心角的弧度数为2,圆心角所对的弦长也为2,那么这个扇形的面积是( )
A. B. C. D.
7.把函数的图像向左平移个单位可以得到函数的图像,若的图像关于y轴对称,则的值为( )
A. B. C.或 D.
8.已知函数(,,)在时取得最大值,且它的最小正周期为,则()
A.的图象过点 B.在上是减函数
C.的一个对称中心是 D.的图象的一条对称轴是
9.要得到函数的图像,可以将函数的图像( )
A.沿x轴向左平移个单位 B.沿x轴向右平移个单位
C.沿x轴向左平移个单位 D.沿x轴向右平移个单位
10. 如果函数 f(x)是定义在(-3 ( http: / / www.21cnjy.com ),3)上的奇函数,当0<x<3时,函数 f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是
A.∪(0,1)∪
B.∪(0,1)∪
C.(- 3,- 1)∪(0,1)∪(1,3)
D.∪(0,1)∪(1,3)
二.填空题(每题5分,共25分)
11.若,那么的值为
12.设为第四象限角,其终边上的一个点是P(x,-),且,则
_______.
13.若 cos(75°+α)=,其中α为第三象限角,则cos(105°-α)+sin(α-105°)= _______.
14.下面有5个命题:
①函数
2x的最小正周期是π.
②若为第二象限角则在一、三、四象限;
③在同一坐标系中,函数y=sin x的图象和函数y=x的图象有3个公共点.
④把函数y=3sin的图象向右平移得到y=3sin 2x的图象.
⑤函数y=sin在[0,π]上是减函数.
其中,真命题的编号是______.(写出所有真命题的编号)
15.函数是常数,且)的部分图象如图所示,下列结论:
①最小正周期为;
②将的图象向左平移个单位,所得到的函数是偶函数;
③;④;
⑤,其中正确的是_______.
三、解答题:(75分)
16.(本小题12分)化简下列各式:
(1);
(2),其中
17. (本小题12分)已知是第三象限角,且
(1)化简 (2)若求的值
(3)若求的值
18.(本小题12分)已知是关于的二次方程的两个实数根,求:(1)的值;(2)的值.
19.(本小题13分)已知函数的部分图象如图所示.
( http: / / www.21cnjy.com / )
(Ⅰ)求函数的解析式;
(Ⅱ)求函数的单调递增区间.
20.(本小题满分13分)已知函数
(1)用五点法在给定的坐标系中作出函数的一个周期的图象;
(2)求函数的单调区间;
(3)求此函数的图象的对称轴方程、对称中心.
( http: / / www.21cnjy.com / )
21.(本小题满分13分)某商品一年内出厂 ( http: / / www.21cnjy.com )价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试分别建立出厂价格、销售价格的模型,并分别求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数;
(3) 求该商店月利润的最大值.
宁远一中2016年上期高一年级第一次月考数学科目试题答案
1.本卷共22题,满分150分,考试时间为120分钟。
2.考生领取到试卷后,应检查试卷是否有缺页漏页,重影模糊等妨碍答题现象,如有请立即向监考老师通报。
一.选择题(每题5分,共50分。在每题后面所给的四个选项中,只有一个是正确的。)
1.的值等于( A )
A.. B. C. D.
2.设,那么( B )
A.B. C. D.
3.已知,则( D )
A.. B. C. D.
A.
5.函数y=﹣x·cosx的部分图象是( D )
A. B.
C. D.
6.如果扇形圆心角的弧度数为2,圆心角所对的弦长也为2,那么这个扇形的面积是( B )
A. B. C. D.
7.把函数的图像向左平移个单位可以得到函数的图像,若的图像关于y轴对称,则的值为( D )
A. B. C.或 D.
8.已知函数(,,)在时取得最大值,且它的最小正周期为,则( C )
A.的图象过点 B.在上是减函数
C.的一个对称中心是 D.的图象的一条对称轴是
9.要得到函数的图像,可以将函数的图像( A )
A.沿x轴向左平移个单位 B.沿x轴向右平移个单位
C.沿x轴向左平移个单位 D.沿x轴向右平移个单位
10. 如果函数 f(x)是定义在(-3, ( http: / / www.21cnjy.com )3)上的奇函数,当0<x<3时,函数 f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( B )
A.∪(0,1)∪
B.∪(0,1)∪
C.(- 3,- 1)∪(0,1)∪(1,3)
D.∪(0,1)∪(1,3)
二.填空题(每题5分,共25分)
11.若,那么的值为 --1
12.设为第四象限角,其终边上的一个点是P(x,-),且,则
_______.
13.若 cos(75°+α)=,其中α为第三象限角,则cos(105°-α)+sin(α-105°)= _______.
14.下面有5个命题:
①函数
2x的最小正周期是π.
②若为第二象限角则在一、三、四象限;
③在同一坐标系中,函数y=sin x的图象和函数y=x的图象有3个公共点.
④把函数y=3sin的图象向右平移得到y=3sin 2x的图象.
⑤函数y=sin在[0,π]上是减函数.
其中,真命题的编号是___①④____.(写出所有真命题的编号)
15.函数是常数,且)的部分图象如图所示,下列结论:
①最小正周期为;
②将的图象向左平移个单位,所得到的函数是偶函数;
③;④;
⑤,其中正确的是_①④⑤______.
三、解答题:(75分)
16.(本小题12分)化简下列各式:
(1);
(2),其中
解:(1)原式=-1
(2)原式=
17. (本小题12分)已知是第三象限角,且
(1)化简 (2)若求的值
(3)若求的值
解:(1) (2) (3)
18.(本小题12分)已知是关于的二次方程的两个实数根,求:(1)的值;(2)的值.
解:(1)
(2) 原式
19.(本小题13分)已知函数的部分图象如图所示.
( http: / / www.21cnjy.com / )
(Ⅰ)求函数的解析式;
(Ⅱ)求函数的单调递增区间.
解:(1)
(2)
20.(本小题满分13分)已知函数
(1)用五点法在给定的坐标系中作出函数的一个周期的图象;
(2)求函数的单调区间;
(3)求此函数的图象的对称轴方程、对称中心.
解:(1)略
(2)单调递增区间: 递减区间:
(3) 对称轴方程是:; 对称中心
21.(本小题满分13分) ( http: / / www.21cnjy.com )某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高价格8元,7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试分别建立出厂价格、销售价格的模型,并分别求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数;
(3) 求该商店月利润的最大值.
解:(1)设出厂价格关于月份的函数为:;
销售价格关于月份的函数为:
依题意得:,
(2) 设月利润函数为:
(3) 该商店月利润的最大值为:
(第10题)
(第10题)
同课章节目录
