湖南省长沙第一中学2024-2025学年高二上学期月考物理试卷(PDF版,含答案)
文档属性
| 名称 | 湖南省长沙第一中学2024-2025学年高二上学期月考物理试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 835.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-12-16 14:52:46 | ||
图片预览




文档简介
湖南省长沙第一中学 2024-2025 学年高二上学期月考物理试卷
一、单选题:本大题共 7 小题,共 28 分。
1.下列情况中系统的动量不守恒的是( )
A. 小车停在光滑水平面上,车上的人在车上走动时,对人与车组成的系统
B. 子弹水平射入放在光滑水平面上的木块中,对子弹与木块组成的系统
C. 子弹射入固定在墙角的木块中,对子弹与木块组成的系统
D. 斜向上抛出的手榴弹在空中炸开时,对手榴弹组成的系统
2.如图所示,一轻质弹簧固定在墙上,一个质量为 的木块以速度 0从右侧沿光滑水平面向左运动并与弹簧
发生相互作用。设相互作用的过程中弹簧始终在弹性限度范围内,那么,在整个相互作用的过程中弹簧对
木块冲量 的大小为( )
A. = 0 B. = 0 C. = 2 0 D. = 3 0
3.如图所示,在光滑水平面上,有一质量为 = 3 的薄板和质量为 = 1 的物块,
都以 = 4 / 的初速度朝相反方向运动,它们之间有摩擦,薄板足够长,当薄板的
速度为2.4 / 时,物块的运动情况是( )
A. 做加速运动 B. 做减速运动 C. 做匀速运动 D. 以上运动都可能
4.长沙经历了长达一月的高温天气,对消防安全造成了极大的挑战,市加强了消防预警等级。通过观察消
防车灭火过程,模拟消防水柱的示意图如图乙所示。水在空中运动, 、 为其运动轨迹上的两点,已知水
在 点时的速度大小为 = 3√ 2 / ,速度方向与竖直方向的夹角为45°,它运动到 点时,速度方向与竖直
方向的夹角为37°( 37° = 0.6),不计空气阻力,重力加速度 取10 / 2,则( )
第 1 页,共 22 页
A. 图中 点是水在空中动量最小的点
B. 水在 点时的速度大小为5 /
C. A、 两点间的高度差为0.9
D. 若消防水柱喷水口流速恒定,水在空中为粗细均匀的曲线水柱
5.一弹丸在飞行到距离地面5 高时仅有水平速度 = 2 / ,爆炸成为甲、乙两块水平飞出,甲、乙的质量
比为3:1,不计质量损失,取重力加速度 = 10 / 2,则下列图中两块弹片飞行的轨迹可能正确的是( )
A. B.
C. D.
6.水上飞行运动使用的是一种叫“喷射式悬浮飞行器”的装置,也称为“喷水飞
行背包”,它通过向下喷射高压水柱的方式将操控者托举在水面上空,利用脚上
喷水装置产生的反冲动力,让你可以在水面之上腾空而起,另外配备有手动控制
的喷嘴,用于稳定空中飞行姿态。如图所示运动员在水上做飞行运动表演。他操
控喷射式悬浮飞行器将水带竖直送上来的水以原速率向下喷出,令自己悬停在空
中。已知运动员与装备的总质量为100 ,两个圆管喷嘴的直径均为10 ,已知
重力加速度大小 = 10 / 2,水的密度为 = 1.0 × 103 / 3,则喷嘴处喷水的速度大约为( )
A. 3.0 / B. 5.6 / C. 8.0 / D. 10.2 /
7.如图所示,由弹性材料制成的物块1和2放置在光滑水平面上,物块2右
侧是用细线悬挂的小球。给物块1一个向右的初速度 0,物块1与物块2发
生弹性碰撞,然后物块2与小球再发生弹性碰撞,碰后小球摆到最大高度
时悬线与竖直方向的夹角为 。在其他条件不变的情况下,换用不同质量
的物块2,发现 的大小与物块2的质量有关。已知物块1的质量为 1,小球的质量为 3,物块2的质量 2满
足以下哪个条件时,夹角 有最大值( )
+ 2+ 2
A. 2 = 1 + 3 B. 2 = √ =
1 3
1 3 C. 2 D. 2 =
1 3
2 2
第 2 页,共 22 页
二、多选题:本大题共 4 小题,共 20 分。
8.水平推力 1和 2分别作用于水平面上等质量的甲、乙两物体上,作用一
段时间后撤去推力,物体将继续运动一段时间后停下来。两物体的 图
像如图所示,图中线段 // ,则整个运动过程中( )
A. 1的冲量大于 2的冲量
B. 1的冲量等于 2的冲量
C. 两物体受到的摩擦力大小相等
D. 摩擦力对甲的冲量小于摩擦力对乙的冲量
9.如图所示,木块 、 并排静止在光滑水平面上,不粘连, 上固定一
竖直轻杆,轻杆上端 点系一长为 的轻质细线,细线另一端系一小球 ,
、 、 质量均为 。现将 拉起至细线水平且自然伸直后由静止释放。
不计空气阻力,重力加速度为 ,下列说法正确的是( )
A. 能向左摆到与释放点等高的位置
B. 第一次运动到最低点过程中, 、 、 构成的系统机械能守恒
C. 第一次运动到最低点时,绳中张力大小为4
D. 从 开始运动到第一次摆到最高点的过程中,绳子拉力对 先做负功再做正功
10.如图所示,水平面上放置着半径为 、质量为3 的半圆形槽, 为
槽的水平直径。质量为 的小球自左端槽口 点的正上方距离为 处由
静止下落,从 点切入槽内。已知重力加速度大小为 ,不计一切摩擦,
下列说法正确的是( )
A. 槽向左运动的最大位移为
B. 小球在槽中运动的最大速度为2√
C. 小球能从 点离开槽,且上升的最大高度等于
8
D. 若槽固定,小球在槽中运动过程中,重力做功的最大功率为 √ 3
9
11.如图甲所示,一轻弹簧的两端分别与质量为 1和 2的两物块相连接,并且静止在光滑的水平面上。现
使 1瞬时获得水平向右的速度3 / ,以此刻为计时零点,两物块的速度随时间变化的规律如图乙所示,已
第 3 页,共 22 页
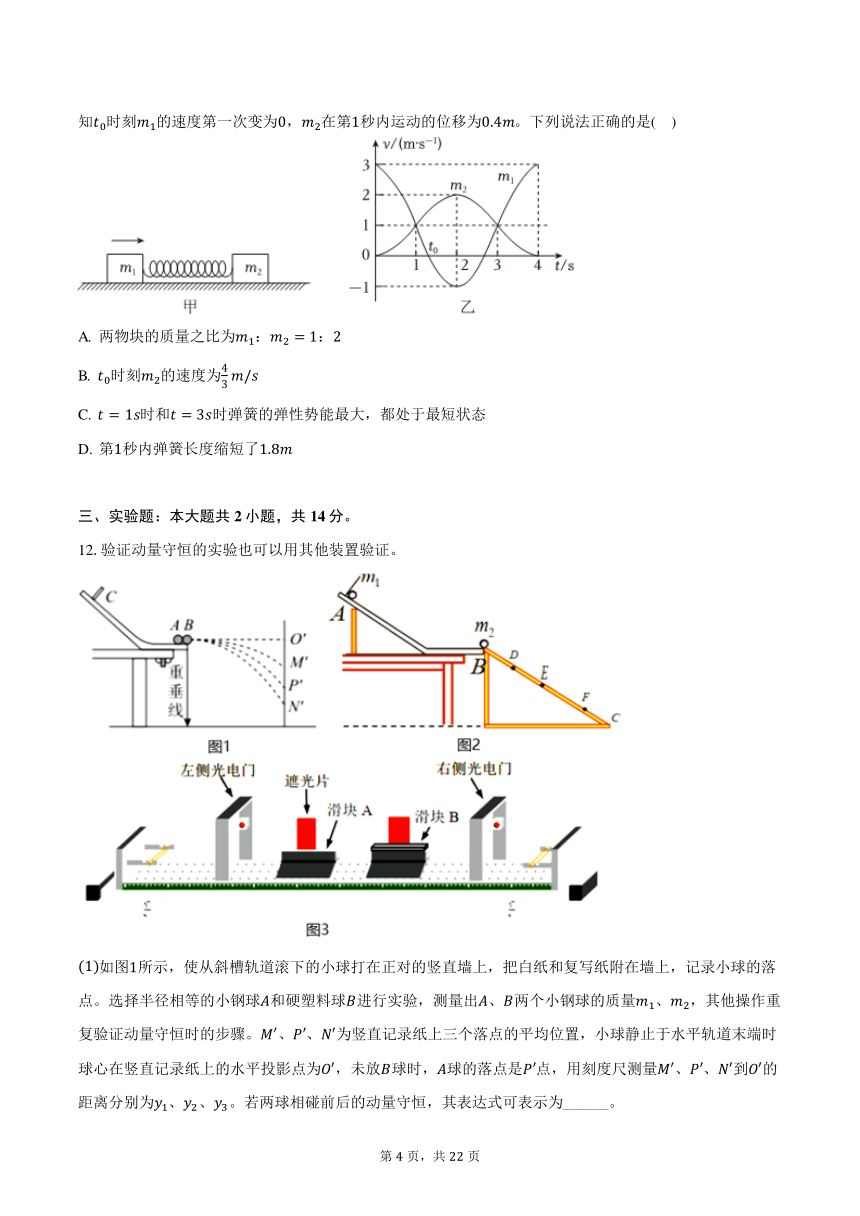
知 0时刻 1的速度第一次变为0, 2在第1秒内运动的位移为0.4 。下列说法正确的是( )
A. 两物块的质量之比为 1: 2 = 1:2
4
B. 0时刻 2的速度为 / 3
C. = 1 时和 = 3 时弹簧的弹性势能最大,都处于最短状态
D. 第1秒内弹簧长度缩短了1.8
三、实验题:本大题共 2 小题,共 14 分。
12.验证动量守恒的实验也可以用其他装置验证。
(1)如图1所示,使从斜槽轨道滚下的小球打在正对的竖直墙上,把白纸和复写纸附在墙上,记录小球的落
点。选择半径相等的小钢球 和硬塑料球 进行实验,测量出 、 两个小钢球的质量 1、 2,其他操作重
复验证动量守恒时的步骤。 ′、 ′、 ′为竖直记录纸上三个落点的平均位置,小球静止于水平轨道末端时
球心在竖直记录纸上的水平投影点为 ′,未放 球时, 球的落点是 ′点,用刻度尺测量 ′、 ′、 ′到 ′的
距离分别为 1、 2、 3。若两球相碰前后的动量守恒,其表达式可表示为______。
第 4 页,共 22 页
1 1 2
A. = +
√ √ √ 2 3 1
1 = 1
2
B. + 2 3
1
C. 1√ 2 = 1√ 3 + 2√ 1
1 1 2
D. = + 2 1
3
(2)用如图2装置也可以验证碰撞中的动量守恒,实验步骤与上述实验类似。图中 、 、 到抛出点 的距离
分别为 、 、 。若两球相碰前后的动量守恒,其表达式可表示为______。
A. 1 = 1 + 2
B. 21 =
2 2
1 + 2
C. 1√ = 1√ + 2√
D. =
(3)如图3所示的水平气垫导轨上,实验时让两滑块分别从导轨的左右两侧向中间运动,滑块运动过程所受
的阻力可忽略,它们穿过光电门后发生碰撞并粘连在一起。实验测得滑块 的总质量为 1、滑块 的总质量
为 2,两滑块遮光片的宽度相同,光电门记录的遮光片挡光时间如表所示。
左侧光电门 右侧光电门
碰前 1 2
碰后 3、 3 无
在实验误差允许范围内,若满足关系式______,即验证了碰撞前后两滑块组成的系统动量守恒。(用测量的
物理量表示)
13.(1)如图所示,在“探究平抛运动规律”的实验中,小华将两个相同的圆弧光滑轨道 、 固定在同一
个竖直平面内,轨道末端均水平,其中 末端与足够长的光滑水平轨道平滑连接。他把质量相等的小钢球
、 分别从两弧面上的相同高度同时静止释放,观察到某一现象,改变释放高度,重复上述操作,仍能观
察到这一现象,由此可以概括出平抛运动的某一规律。小华观察到的现象和反映的平抛运动规律是______。
A. 、 两个小球相撞
B. 、 两个小球同时落地
C.水平方向做匀速直线运动
D.竖直方向做自由落体运动
(2)小芳利用图2中甲图装置进行实验,每次释放小球的位置都相同,并在乙图的坐标纸上记录了小球经过
的 、 、 三点,已知坐标纸每小格的边长 = 5 ,该小球做平抛运动的初速度大小为______ / ( 取
第 5 页,共 22 页
10 / 2,结果保留2位有效数字)。
(3)小燕在研究平抛运动时发现,若小球下落相同高度,平抛初速度越大,水平射程也越大,依据这一规律,
2 1
她用如图3所示装置来“验证动量守恒定律”:碰撞恢复系数的定义为 = | | ,其中 和 分别是20 10 10 20
碰撞前两小球的速度, 1和 2分别是碰撞后两小球的速度,该实验小球碰撞恢复系数的表达式为 =______(
用题目中字母 、 、 表达),若测得 =______,可以判定小球的碰撞为弹性碰撞。
四、计算题:本大题共 3 小题,共 38 分。
14.一长为 ,质量为 = 3 的木板静止在光滑的水平面上,一质量为 = 1 的滑块以初速度 0 = 4 / 滑
到木板上,木板长度 至少为多少才能使滑块不滑出木板。(滑块与木板间动摩擦因数 = 0.3, 取10 / 2)
15.如图所示,质量均为 的物块 、 用绕过光滑轻质定滑轮的不可伸长的刚性轻绳
连接, 与地面接触, 离地面的高度 为1.2 ,质量为2 的圆环 套在轻绳上, 在
上方 = 0.8 处。由静止释放圆环 , 下落后与 碰撞并粘在一起,碰撞时间极短,
不计 与绳之间的摩擦和空气阻力, 、 、 均可视为质点,重力加速度取10 / 2,
求:
第 6 页,共 22 页
(1) 、 碰撞后瞬间,共同速度为多大;
(2)碰撞后, 经过多长时间到达地面。
16.如图所示,水平地面上放有木板 、 ,木板 的右侧有竖直墙, 板长度为 = 2 ,木板 与地面间的
动摩擦因数为 = 0.1,可视为质点的物块 静置于木板 的左端。不可伸长的轻绳一端系于 点,另一端拴
一小球 ,钉子 位于物块 的正上方, 间距等于绳长的一半, 连线与水平方向的夹角 = 37°,初始
锁定木板 ,将小球 从绳水平拉直的位置由静止释放,到达最低点时与静止的物块 发生碰撞,碰后小球
反弹到达最高点时,轻绳刚好离开钉子 ;物块 滑至木板 右端时,二者共速,且此时木板 与木板 发生
碰撞;碰后木板 恰好能返回初始位置。已知木板 和物块 的质量均为 = 0.3 ,所有碰撞均为弹性碰撞,
物块 与两木板间的动摩擦因数相同,重力加速度大小 = 10 / 2, 37° = 0.6。求:
(1)物块 与木板间的动摩擦因数 ;
(2) 右端到 左端的初始间距为 0;
(3)小球 的质量 ;
(4)若 的右端距墙为0.5 ,现在解除 的锁定,小球 仍由绳水平拉直的位置从静止释放,最终 在 上未
掉下,已知木板 的质量 = 0.9 ,木板 与地面间的摩擦忽略不计, 碰墙后取走 。求木板 的最小长
度 。
第 7 页,共 22 页
答案和解析
1.【答案】
【解析】解: 、小车停在光滑水平面上,车上的人在车上走动时,对人与车组成的系统所受合外力为零,
动量守恒,故 A 错误;
B、子弹水平射入放在光滑水平面上的木块中,对子弹与木块组成的系统所受合外力为零,动量守恒,故 B
错误;
C、子弹射入固定在墙角的木块中,对子弹与木块组成的系统所受合外力不为零,动量不守恒,故 C正确;
D、斜向上抛出的手榴弹在空中炸开时,对手榴弹组成的系统内力远大于外力,动量守恒,故 D 错误;
故选: 。
根据动量守恒定律的条件结合题目选项逐一完成分析。
本题主要考查了动量守恒定律的相关应用,理解动量守恒的条件即可完成分析,难度不大。
2.【答案】
【解析】解:根据题意分析可以知道,木块离开弹簧的瞬间速度大小为 0,方向向右,取向左为正方向,
根据动量定理有
= 0 0 = 2 0,负号代表方向向右;
故 ABD 错误,C正确;
故选: 。
根据动量定理,规定正方向,可求得弹簧对木块的冲量 。
本题考查动量定理,运用过程应注意规定正方向。
3.【答案】
【解析】解:开始阶段, 向右减速, 向左减速,根据系统的动量守恒定律得:当 的速度为零时,设此
时 的速度为 1 .规定向右为正方向,根据动量守恒定律得:
( ) = 1
代入解得: 1 = 2.67 / 。
此后 将向右加速, 继续向左减速;当两者速度达到相同时,设共同速度为 2 .规定向右为正方向,由动
量守恒定律得:
( ) = ( + ) 2,
代入解得: 2 = 2 / 。
第 8 页,共 22 页
两者相对静止后,一起向右做匀速直线运动。
由此可知当 的速度为2.4 / 时, 处于向右加速过程中。故 A 正确,BCD 错误;
故选: 。
分析物体的运动情况:初态时,系统的总动量方向水平向右,两个物体开始均做匀减速运动, 的速度先减
至零,根据动量守恒定律求出此时 的速度.之后, 向右做匀加速运动, 继续向右做匀减速运动,最后
两者一起向右匀速运动.根据动量守恒定律求出薄板的速度大小为2.4 / 时,物块的速度,并分析 的运
动情况.
本题考查应用系统的动量守恒定律分析物体运动情况的能力,这是分析物体运动情况的一种方法,用得较
少,但要学会,比牛顿定律分析物体运动情况简单.
4.【答案】
【解析】解: .水运动至最高点时,速度最小,则此时动量最小,故 A 错误;
√ 2
0 0 45°
B.水在 、 两点的水平分速度相等,则 45° = , 37° = ,得 = = 2 × 3√ 2 / = 5 / ,
37 0.6
故 B 正确;
√ 2
C. 、 两点的竖直分速度分别为 = 45° = 3√ 2 × / = 3 / , = 37° = 5 × 0.8 / =2
2
2 2 4 3
2
4 / ,由 = 2 ,解得 、 两点间的高度差为 = = 0.35 ,故 C错误。 2×10
D.若消防水柱喷水口流速恒定,则任意相等时间内流出水的质量相等,水在空中做匀变速曲线运动,速度
大的地方水柱细,速度小的地方水柱粗,故 D 错误。
故选: 。
A、水运动至最高点时速度最小,则此时动量最小;
B、水在 、 两点的水平分速度相等,根据几何关系列出方程式解答;
C、求出在 、 两点的竖直分速度,运用速度—位移公式解答;
D、水在空中做匀变速曲线运动,速度大的地方水柱细,速度小的地方水柱粗。
考查对动量定理的理解,运动的合成与分解方法的运用,运用方程式解答。
5.【答案】
【解析】解:规定向右为正,设弹丸的质量为4 ,则甲的质量为3 ,乙的质量为 ,炮弹到达最高点时爆
炸时,爆炸的内力远大于重力(外力),遵守动量守恒定律,则有:
4 0 = 3 1 + 2
则8 = 3 1 + 2
第 9 页,共 22 页
2 2×5
两块弹片都做平抛运动,高度一样,则运动时间相等, = √ = √ = 1 ,
10
水平方向做匀速运动, 1 = 1 = 1, 2 = 2 = 2,
则8 = 3 1 + 2
结合图象可知, 的位移满足上述表达式,故 B 正确。
故选: 。
炮弹到达最高点时爆炸时,爆炸的内力远大于重力(外力),遵守动量守恒定律;
当炮弹到达最高点时爆炸为沿水平方向运动的两片,两片炸弹都做平抛运动.根据平抛运动的基本公式即
可解题.
本题考查了动量守恒定律的直接应用,知道当炮弹到达最高点时爆炸为沿水平方向运动的两片,两片炸弹
都做平抛运动,难度适中.
6.【答案】
【解析】解:设飞行器对水的平均作用力为 ,根据牛顿第三定律可知,水对飞行器的作用力大小也为 ,
对运动员与装备由平衡条件得: = = 100 × 10 = 1000
设喷嘴处喷水的速度大小为 ,两个圆管喷嘴的横截面积为 ,在时间 内喷出的水的质量为:
= = 2
取竖直向下为正方向,根据动量定理可得 时间内质量为 的水获得的冲量为:
= + = 2
可得: + 2 = 4 2,当 → 0时,2 → 0,解得:
= √
4
又有: = ( )2,其中 = 10 = 0.1
2
代入数据解得: ≈ 5.6 / ,故 ACD 错误,B 正确。
故选: 。
对运动员与装备由平衡条件求得水对飞行器的作用力大小,根据牛顿第三定律可知飞行器对水的作用力,
根据动量定理求解喷嘴处喷水的速度大小。
本题考查了动量定理的应用,属于流体冲击模型,取一段时间内相互作用的流体为研究对象,应用动量定
理解答。
7.【答案】
第 10 页,共 22 页
【解析】解:物块1与物块2发生弹性碰撞,碰撞过程系统动量守恒、机械能守恒,
以向右为正方向,由动量守恒定律得: 1 0 = 1 1 + 2 2
1 2 1 1由机械能守恒定律得: 1 0 = 1
2 + 2
2 2 1 2 2
2
2
解得: 12 = 1+ 02
物块2与小球3发生弹性碰撞,碰撞过程系统动量守恒、机械能守恒,
以向右为正方向,由动量守恒定律得: 2 2 = 2 2′ + 3 3
1 1 1
由机械能守恒定律得: 22 2 = 2 ′
2
2 +
2
3 3 2 2 2
2 4 4
解得: = 2 2 1 2 0 1 03 = = 2+ 3 ( 1+ )( + ) + +( 1 32 2 3 1 3 + 2) 2
1
设细线的长度为 ,碰撞后小球上升过程机械能守恒,由机械能守恒定律得: 23 3 = 3 (1 ) 2
2
解得: = 1 3 , 是减函数, 越大, 越小,由于 、 一定 3越大 越小,则 越大, 2
当 2 =
1 3,即 2 = √ 1 3时碰撞后小球的速度 3最大,夹角 最大,故 B 正确,ACD 错误。 2
故选: 。
弹性碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律求出碰撞后小球速度,然
后分析判断答题。
本题考查了动量守恒定律的应用,分析清楚运动过程,应用动量守恒定律与机械能守恒定律可以解题。
8.【答案】
【解析】解: 、甲、乙先做加速运动,撤去推力后做减速运动。题图中线段 // ,表明甲、乙两物体
做匀减速运动的加速度相同,依题意,二者质量相等,由牛顿第二定律
=
可知两物体受到的摩擦力大小相等。故 C正确;
、由题图可知,整个运动过程中两物体的始末速度均为零,所以动量改变量均为零,那么合力的冲量
为零: + = 0
可知推力的冲量大小等于物体受到的摩擦力的冲量大小。由题图可知甲的运动时间小于乙的运动时间,所
以摩擦力对甲的冲量小于摩擦力对乙的冲量,则 1的冲量小于 2的冲量,故 AB 错误;D 正确。
故选: 。
由速度图象分析可知,水平推力撤去后, 与 平行,说明加速度相同,动摩擦因数相同,两物体的质量
相等,说明摩擦力大小相等;
第 11 页,共 22 页
根据动量定理,研究整个过程,确定两个推力的冲量关系。
本题首先考查读图能力,其次考查动量定理应用;能够根据全过程动量定理进行求解即可。
9.【答案】
【解析】解: .当 第一次到达左侧最高处时, 、 都有速度,即都有动能,根据系统机械能守恒可知, 第
一次到达左侧最高处时的高度比释放高度低,故 A 错误;
B. 第一次运动到最低点过程中,全程只有重力做功,所以 、 、 构成的系统机械能守恒,故 B 正确;
C. 第一次运动到最低点过程中, 、 一起向右运动,当 第一次到达最低点时, 和 即将分离,则有
= = = 2
第一次运动到最低点过程中,由重力和绳子张力的合力提供向心力,则
( 2 + )
=
第一次运动到最低点过程中, 、 、 构成的系统机械能守恒,则
1 1
2 + 2 × 2 =
2 2
解得
= 4
故 C正确;
D. 第一次运动到最低点过程中, 、 向右运动,此时小球的速度方向与绳子的夹角为钝角,绳子对小球
做负功; 从最低点到左侧最高点过程中, 、 分离, 以原速度做匀速直线运动, 速度减为零后反方向
向左运动,当 、 速度相等时, 球摆到最高点,此过程小球的速度与绳子的夹角先为锐角后为钝角,所
以绳子对小球先做正功再做负功,所以从 开始运动到第一次摆到最高点的过程中,绳子拉力对 先做负功
再做正功最后做负功,故 D 错误。
故选: 。
A.由系统机械能守恒得出结论,且整体机械能守恒,从而进行分析;
B. 第一次运动到最低点过程中, 一起向右运动,当 第一次到达最低点时, 和 即将分离,再根据 做
圆周运动以及 第一次到最低点机械能守恒列式求解;
C.根据圆周运动公式和机械能守恒求 第一次运动到最低点时,绳中张力大小;
D. 第一次运动到最低点过程中, 向右运动,可知此时小球的速度与绳子的夹角为钝角, 从最低点到左
侧最高点过程中, 分离, 以原速度做匀速直线运动, 速度减为零后反方向向左运动,当 速度相等
时, 球摆到最高点,此过程小球的速度与绳子的夹角先为锐角后为钝角。
本题主要是考查机械能守恒定律,主要需熟练掌握整体分析机械能守恒得应用。
第 12 页,共 22 页
10.【答案】
【解析】解: .半圆形槽和小球在水平方向合力为零,水平方向上动量守恒,设小球水平方向分速度大小为
1,槽的速度大小为 2,以向右方向为正方向,则
1 = 3 2
当小球运动到 点时,小球和槽的水平位移最大,设小球的水平位移大小为 1,槽的位移大小为 2,半圆形
槽和小球运动时间相同,则
1 = 3 2
半圆形槽和小球在水平方向上位移大小之和,即相对位移大小为
1 + 2 = 2
解得
2 = 0.5
故 A 错误;
B.若槽固定,小球运动到最低点时速度最大,由机械能守恒
1
2 = 2 2
解得
= 2√
故 B 错误;
C.小球运动 点时,小球和槽在水平方向上速度相同,根据水平方向动量守恒,则此时小球和槽在水平方向
上的速度都为零,根据小球和槽组成的系统机械能守恒,则小球上升的最大高度等于 ,故 C正确;
D.根据功率公式
0 =
可知,当小球在竖直方向分速度最大时,重力的功率最大,设此时小球和 点连线与竖直方向的夹角为 ,
此时速度大小为 ,由动能定理
1
(1 + ) = 2
2
解得
= √ 2 (1 + )
则竖直方向分速度为
= √ 2 (1 + ) = √ 2 (1 + )(1 cos
2 )
第 13 页,共 22 页
1
根据数学求极值的方法可知,当 = 时,竖直方向分速度最大,最大值为
3
8
= √ 3 9
重力做功的最大功率为
=
解得
8
= √ 3 9
故 D 正确。
故选: 。
小球和半圆形槽组成的系统除重力和弹力外不受其他外力,所以整个系统机械能守恒;但是系统在水平方
向上不受任何外力,故水平方向动量守恒。再根据水平动量守恒及整体的机械能守恒进行求解即可。
本题考查了动量与能量的综合应用;解题的关键在于分析小球与半圆形槽组成的系统水平动量守恒,而竖
直方向动量不守恒;整体的机械能守恒。
11.【答案】
【解析】解: .从 = 0开始到 1时刻,取向右为正方向,根据动量守恒定律,有
1 1 = ( 1 + 2) 2
将 1 = 3 / , 2 = 1 / 代入得
1: 2 = 1:2
故 A 正确;
B.从 = 0开始到 0时刻,取向右为正方向,根据动量守恒定律
1 0 = 2 ′2
代入数据解得 2的速度为
3
′2 = / 2
故 B 错误;
C.两物体速度相等时,弹簧的形变量最大,弹性势能最大,但在 = 1 时刻弹簧处于压缩状态,在 = 3 时
刻弹簧处于伸长状态,故 C错误;
D.若考虑两物体从 = 1 到 = 2 的时间内, 2加速运动, 1减速运动,因
1: 2 = 1:2
则在任意时刻两物体的加速度之比为
第 14 页,共 22 页
1: 2 = 2:1
若用微元法考虑,则两物体间的距离
1 1 1 1
= 1 +
2
2 ( 1
2
1 ) =
2
2 + 1
2
2 2 2 2
1
则“ 2
2 2
”对应的位移(面积)为
1 × 1 0.4 = 0.6
1 1
则“ 21 ”对应的位移(面积)为“
2
2 ”对应的位移(面积)的2倍,即为1.2 ,该两部分面积之和与0~1 2 2
内对应的虚线面积相等,如图所示
为1.2 + 0.6 = 1.8 ,即0~1 内弹簧的长度缩短1.8 ,故 D 正确。
故选: 。
从 = 0开始到 1时刻,根据动量守恒定律求解质量之比;从 = 0开始到 0时刻,根据动量守恒定律求解 0时
刻 2的速度;两物体共速的时候,弹簧的形变量最大,弹性势能最大,根据 图像可知判断弹簧处于压
缩还是拉伸状态;根据 图像求解位移,位移之差为弹簧的压缩量。
本题考查动量与量能的综合应用,要求学生能正确分析物体的运动过程,熟练应用对应的规律解题。
+
12.【答案】 1 2 1 2 =
1 2 3
【解析】解:(1)碰撞前, 1落在图中的 ′点,设其水平初速度为 1,小球 1和 2发生碰撞后, 1的落点
在图中 ′点,设其水平初速度为 1′, 2的落点是图中的 ′点,设其水平初速度为 2,设斜面 与水平面
的倾角为 ,
1
由平抛运动规律得 2 =
2, = 1 2
解得: 1 = √ 2 2
同理可得 ′1 = √ , = 2 2 √1 2 3
碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得 1 1 = 1 1′ + 2 2
整理得 1
= 1 + 2
√ 2 √ 3 √ 1
第 15 页,共 22 页
故 A 正确,BCD 错误;
故选: 。
(2)碰撞前, 1落在图中的 点,设其水平初速度为 1 .小球 1和 2发生碰撞后, 1的落点在图中 点,设
其水平初速度为 1 ′, 2的落点是图中的 点,设其水平初速度为 2 .设斜面 与水平面的倾角为 ,
1
由平抛运动规律得: =
2, = 2 1 ,
cos2
解得: 1 = √
2
√ cos
2 cos2
同理可得: 1 ′ = , = √
,
2 2 2
碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得: 1 1 = 1 1′ + 2 2,
整理得: 1√ = 1√ + 2√ ;
故 ABD 错误,C正确;
故选: 。
(3)若让两滑块分别从导轨的左右两侧向中间运动,选取向右为正方向,则有:
1 1 2 2 = ( 1 + 2) 3,
设遮光片的宽度为 ,则: 1 = , 2 = , 3 = , 1 2 3
联立可得: 1
2 + = 1 2
1 2 3
+
故答案为:(1) ;(2) ;(3) 1 2 = 1 2
1 2 3
(1)(2)根据水平方向上的分运动即可验证动量守恒;根据动量守恒定律以及平抛运动规律可确定对应的表达
式。
(3)根据题意应用动量守恒定律求出实验需要验证的表达式。
本题主要考查了动量守恒定律的验证实验,根据实验原理掌握正确的实验操作,结合平抛运动在水平方向
上匀速直线运动的特点完成表达式的分析,同时改进了实验,对学生的要求较高,难度较大。
13.【答案】 1.5 1
【解析】解:(1)该同学观察到的现象是 、 两个小球相撞,说明两球在水平方向的运动完全相同,即反映
平抛运动的规律是水平方向做匀速直线运动,故 AC正确,BD 错误;
故选: 。
2 2×5×10 2
(2)对竖直方向根据公式 = 2,得 = √ = √ = 0.1 ;
10
3 3×5×10 2
对水平方向: 0 = = / = 1.5 / 。 0.1
第 16 页,共 22 页
(3)本实验的原理小球从槽口飞出后作平抛运动的时间相同,设为 ,则有: = 10 , = 1 , = 2 ,
| 2 1 | | | 小球2碰撞前静止,即: 20 = 0,因而碰撞系数为: = = = 。 | 20 10 | |0 |
因为可用小球做平抛运动的水平射程来代替小球抛出时的速度,规定向右为正方向,根据动量守恒有:
1 10 = 1 1 + 2 2
1 1 1
若碰撞过程为弹性碰撞,则机械能守恒,有: 2 2 2
2 1
10 = 1 1 + 2 2 2 2,
整理可得 10 = 2 1
则当 = 1时可以判定小球的碰撞为弹性碰撞。
故答案为:(1) ;(2)1.5;(3) ,1
(1)根据平抛运动的特点判断出实验揭示的规律;
(2)利用平抛运动的公式求初速度;
(3)小球做平抛运动的水平射程来代替小球抛出时的速度,由动量守恒定律和机械能守恒定律求出需要验证
的表达式。
本题考查探究平抛运动规律和验证动量守恒定律,在验证动量守恒定律中,要注意明确实验原理,学会实
验方法;学会在相同高度下,利用平抛运动的水平射程来间接测出速度,并能推导相应的动量守恒表达式
及机械能守恒定律表达式。
14.【答案】解:滑块与木板组成的系统动量守恒,滑块不从木板上滑出,则滑块与木板有相同的末速度,
设末速度大小为 ,滑块与木板的相对位移大小为 。以向右为正方向,对滑块与木板组成的系统由动量守
恒定律得:
0 = ( + )
根据能量守恒定律与功能关系得:
1
= 2
1
0 ( + )
2
2 2
2
联立可得: = 0
2 ( + )
代入数据得: = 2
要使滑块不滑出木板,其长度 至少等于 = 2 。
答:木板长度 至少为2 才能使滑块不滑出木板。
【解析】滑块与木板组成的系统动量守恒,滑块不从木板上滑出,临界条件是滑块与木板共速后,滑块与
木板的相对位移大小恰好等于板长。应用动量守恒定律,结合功能关系解答。
第 17 页,共 22 页
本题考查了动量守恒定律在板块模型中的应用,此题类似于完全非弹性碰撞,损失的机械能转化为摩擦生
热。
15.【答案】解:(1) 与 碰撞前的运动过程,对 ,由机械能守恒定律有
1
2 = × 2 2
2
解得: = 4 /
设 与 碰撞后共同速度为 ,取竖直向下为正方向,以 、 、 组成的系统为研究对象,由动量守恒定律有
2 = ( + + 2 )
解得: = 2 /
(2) 与 碰撞后粘在一起,一起向下做匀加速直线运动,对 、 、 整体,根据牛顿第二定律有
3 = 4
解得: = 2.5 / 2
由运动学公式有
1
= + 2
2
解得碰撞后 到达地面的时间为: = 0.4
答:(1) 、 碰撞后瞬间,共同速度为2 / ;
(2)碰撞后, 经过0.4 时间到达地面。
【解析】(1)对 与 碰撞前的运动过程,根据机械能守恒定律列式,求出 与 碰撞前的速度,根据动量守
恒定律求出碰撞后共同速度大小;
(2) 与 碰撞后粘在一起,根据牛顿第二定律求出加速度,再根据运动学公式求碰撞后 到达地面的时间。
本题是含有非弹性碰撞的类型,要理清物体的运动过程,把握碰撞的基本规律:动量守恒定律。要注意明
确研究对象,采用整体法求连接体的加速度大小,也可以运用隔离法求加速度大小。
16.【答案】解:(1) 在 上滑行时,对 ,有
( + ) = 1
解得
1 = ( 2 )
碰 后,对 ,有
= 2
解得
2 = = 0.1 × 10 /
2 = 1 / 2
第 18 页,共 22 页
木板 锁定, 碰 后恰能返回初始位置,则碰撞前后 的加速度大小相等
1 = 2
解得
= 3 = 3 × 0.1 = 0.3
(2) 在 上滑行时,对 ,有
=
解得
= 3 /
2
在 上滑行的过程中
1 = 1 1
C、 的位移相对关系
1 1
( + ) = 2 共 1 2 共 1
解得 在 上向右滑行的初速度
= 4 /
时间
1 = 1 1内 向前滑行的距离
1
0 = 1
2
1 2
解得
0 = 0.5
(3)小球 下摆过程中
1
( 37° + ) = 2
2 2 2 1
解得
1 = 4√
小球 碰后反弹上摆过程中
1
( 37°) = 2 2 2 2 2
解得
2 = 2√
小球 碰 ,以 1的方向为正方向,根据动量守恒
第 19 页,共 22 页
1 = 2 +
根据能量守恒定律
1
2
1 1
1 =
2 2
2 2 2
+
2
解得
= = 0.1
3
绳长
= 4
(4)解除 锁定后, 、 共速
1 = 1 1
解得
1 = 1 /
方向向右
碰 ,以向右的方向为正方向,对 、 ,根据动量守恒
1 = + 1
根据能量守恒定律
1 1
2 = 2
1
1 +
2
2 2 2 1
解得
1
= / 2
方向向左
1
1 = / 2
方向向右
设 、 达到共同速度 2中, 未碰墙,以向右方向为正方向,根据动量守恒有
1 + 1 = ( + ) 2
解得
5
2 = / , 8
方向向右
设 在 上向右滑过 1,有
第 20 页,共 22 页
1 1 1
=
2 2 2
1 2 1
+
2 1
( + )
2 2
解得
1
1 = 32
此过程中 的对地位移为 1,有
1 1
=
2 2
1 2 2 2 1
解得
9
1 = < 128 0
未碰墙,之后 、 一起匀速运动,碰墙反弹后 、 达到共同速度 3中,以向左为正,根据动量守恒有
2 2 = ( + ) 3
解得
5
3 = / , 16
方向向左
设此过程中 在 上继续向右滑过 2,有
1 1
2 2 2 = ( + ) 2 ( + ) 2 2 3
解得
25
2 = 128
之后 碰 时, 相对 向前滑行,故为了 不掉下, 板的最小长度为
= 1 + 2
解得
29
=
128
答:(1)物块 与木板间的动摩擦因数为0.3;
(2) 右端到 左端的初始间距为为0.5 ;
(3)小球 的质量 为0.1 ;
29
(4)木板 的最小长度 为 。
128
【解析】(1)根据牛顿第二定律求物块 与木板间的动摩擦因数 ;
(2)根据牛顿第二定律和运动学公式求 右端到 左端的初始间距为 0;
(3)根据动量守恒和能量守恒定律求小球 的质量 ;
第 21 页,共 22 页
(4)根据动量守恒和动能定理求木板 的最小长度 。
本题考查受力分析、动能定理、功能关系,物体运动过程中应用动能定理、功能原理解决问题。
第 22 页,共 22 页
一、单选题:本大题共 7 小题,共 28 分。
1.下列情况中系统的动量不守恒的是( )
A. 小车停在光滑水平面上,车上的人在车上走动时,对人与车组成的系统
B. 子弹水平射入放在光滑水平面上的木块中,对子弹与木块组成的系统
C. 子弹射入固定在墙角的木块中,对子弹与木块组成的系统
D. 斜向上抛出的手榴弹在空中炸开时,对手榴弹组成的系统
2.如图所示,一轻质弹簧固定在墙上,一个质量为 的木块以速度 0从右侧沿光滑水平面向左运动并与弹簧
发生相互作用。设相互作用的过程中弹簧始终在弹性限度范围内,那么,在整个相互作用的过程中弹簧对
木块冲量 的大小为( )
A. = 0 B. = 0 C. = 2 0 D. = 3 0
3.如图所示,在光滑水平面上,有一质量为 = 3 的薄板和质量为 = 1 的物块,
都以 = 4 / 的初速度朝相反方向运动,它们之间有摩擦,薄板足够长,当薄板的
速度为2.4 / 时,物块的运动情况是( )
A. 做加速运动 B. 做减速运动 C. 做匀速运动 D. 以上运动都可能
4.长沙经历了长达一月的高温天气,对消防安全造成了极大的挑战,市加强了消防预警等级。通过观察消
防车灭火过程,模拟消防水柱的示意图如图乙所示。水在空中运动, 、 为其运动轨迹上的两点,已知水
在 点时的速度大小为 = 3√ 2 / ,速度方向与竖直方向的夹角为45°,它运动到 点时,速度方向与竖直
方向的夹角为37°( 37° = 0.6),不计空气阻力,重力加速度 取10 / 2,则( )
第 1 页,共 22 页
A. 图中 点是水在空中动量最小的点
B. 水在 点时的速度大小为5 /
C. A、 两点间的高度差为0.9
D. 若消防水柱喷水口流速恒定,水在空中为粗细均匀的曲线水柱
5.一弹丸在飞行到距离地面5 高时仅有水平速度 = 2 / ,爆炸成为甲、乙两块水平飞出,甲、乙的质量
比为3:1,不计质量损失,取重力加速度 = 10 / 2,则下列图中两块弹片飞行的轨迹可能正确的是( )
A. B.
C. D.
6.水上飞行运动使用的是一种叫“喷射式悬浮飞行器”的装置,也称为“喷水飞
行背包”,它通过向下喷射高压水柱的方式将操控者托举在水面上空,利用脚上
喷水装置产生的反冲动力,让你可以在水面之上腾空而起,另外配备有手动控制
的喷嘴,用于稳定空中飞行姿态。如图所示运动员在水上做飞行运动表演。他操
控喷射式悬浮飞行器将水带竖直送上来的水以原速率向下喷出,令自己悬停在空
中。已知运动员与装备的总质量为100 ,两个圆管喷嘴的直径均为10 ,已知
重力加速度大小 = 10 / 2,水的密度为 = 1.0 × 103 / 3,则喷嘴处喷水的速度大约为( )
A. 3.0 / B. 5.6 / C. 8.0 / D. 10.2 /
7.如图所示,由弹性材料制成的物块1和2放置在光滑水平面上,物块2右
侧是用细线悬挂的小球。给物块1一个向右的初速度 0,物块1与物块2发
生弹性碰撞,然后物块2与小球再发生弹性碰撞,碰后小球摆到最大高度
时悬线与竖直方向的夹角为 。在其他条件不变的情况下,换用不同质量
的物块2,发现 的大小与物块2的质量有关。已知物块1的质量为 1,小球的质量为 3,物块2的质量 2满
足以下哪个条件时,夹角 有最大值( )
+ 2+ 2
A. 2 = 1 + 3 B. 2 = √ =
1 3
1 3 C. 2 D. 2 =
1 3
2 2
第 2 页,共 22 页
二、多选题:本大题共 4 小题,共 20 分。
8.水平推力 1和 2分别作用于水平面上等质量的甲、乙两物体上,作用一
段时间后撤去推力,物体将继续运动一段时间后停下来。两物体的 图
像如图所示,图中线段 // ,则整个运动过程中( )
A. 1的冲量大于 2的冲量
B. 1的冲量等于 2的冲量
C. 两物体受到的摩擦力大小相等
D. 摩擦力对甲的冲量小于摩擦力对乙的冲量
9.如图所示,木块 、 并排静止在光滑水平面上,不粘连, 上固定一
竖直轻杆,轻杆上端 点系一长为 的轻质细线,细线另一端系一小球 ,
、 、 质量均为 。现将 拉起至细线水平且自然伸直后由静止释放。
不计空气阻力,重力加速度为 ,下列说法正确的是( )
A. 能向左摆到与释放点等高的位置
B. 第一次运动到最低点过程中, 、 、 构成的系统机械能守恒
C. 第一次运动到最低点时,绳中张力大小为4
D. 从 开始运动到第一次摆到最高点的过程中,绳子拉力对 先做负功再做正功
10.如图所示,水平面上放置着半径为 、质量为3 的半圆形槽, 为
槽的水平直径。质量为 的小球自左端槽口 点的正上方距离为 处由
静止下落,从 点切入槽内。已知重力加速度大小为 ,不计一切摩擦,
下列说法正确的是( )
A. 槽向左运动的最大位移为
B. 小球在槽中运动的最大速度为2√
C. 小球能从 点离开槽,且上升的最大高度等于
8
D. 若槽固定,小球在槽中运动过程中,重力做功的最大功率为 √ 3
9
11.如图甲所示,一轻弹簧的两端分别与质量为 1和 2的两物块相连接,并且静止在光滑的水平面上。现
使 1瞬时获得水平向右的速度3 / ,以此刻为计时零点,两物块的速度随时间变化的规律如图乙所示,已
第 3 页,共 22 页
知 0时刻 1的速度第一次变为0, 2在第1秒内运动的位移为0.4 。下列说法正确的是( )
A. 两物块的质量之比为 1: 2 = 1:2
4
B. 0时刻 2的速度为 / 3
C. = 1 时和 = 3 时弹簧的弹性势能最大,都处于最短状态
D. 第1秒内弹簧长度缩短了1.8
三、实验题:本大题共 2 小题,共 14 分。
12.验证动量守恒的实验也可以用其他装置验证。
(1)如图1所示,使从斜槽轨道滚下的小球打在正对的竖直墙上,把白纸和复写纸附在墙上,记录小球的落
点。选择半径相等的小钢球 和硬塑料球 进行实验,测量出 、 两个小钢球的质量 1、 2,其他操作重
复验证动量守恒时的步骤。 ′、 ′、 ′为竖直记录纸上三个落点的平均位置,小球静止于水平轨道末端时
球心在竖直记录纸上的水平投影点为 ′,未放 球时, 球的落点是 ′点,用刻度尺测量 ′、 ′、 ′到 ′的
距离分别为 1、 2、 3。若两球相碰前后的动量守恒,其表达式可表示为______。
第 4 页,共 22 页
1 1 2
A. = +
√ √ √ 2 3 1
1 = 1
2
B. + 2 3
1
C. 1√ 2 = 1√ 3 + 2√ 1
1 1 2
D. = + 2 1
3
(2)用如图2装置也可以验证碰撞中的动量守恒,实验步骤与上述实验类似。图中 、 、 到抛出点 的距离
分别为 、 、 。若两球相碰前后的动量守恒,其表达式可表示为______。
A. 1 = 1 + 2
B. 21 =
2 2
1 + 2
C. 1√ = 1√ + 2√
D. =
(3)如图3所示的水平气垫导轨上,实验时让两滑块分别从导轨的左右两侧向中间运动,滑块运动过程所受
的阻力可忽略,它们穿过光电门后发生碰撞并粘连在一起。实验测得滑块 的总质量为 1、滑块 的总质量
为 2,两滑块遮光片的宽度相同,光电门记录的遮光片挡光时间如表所示。
左侧光电门 右侧光电门
碰前 1 2
碰后 3、 3 无
在实验误差允许范围内,若满足关系式______,即验证了碰撞前后两滑块组成的系统动量守恒。(用测量的
物理量表示)
13.(1)如图所示,在“探究平抛运动规律”的实验中,小华将两个相同的圆弧光滑轨道 、 固定在同一
个竖直平面内,轨道末端均水平,其中 末端与足够长的光滑水平轨道平滑连接。他把质量相等的小钢球
、 分别从两弧面上的相同高度同时静止释放,观察到某一现象,改变释放高度,重复上述操作,仍能观
察到这一现象,由此可以概括出平抛运动的某一规律。小华观察到的现象和反映的平抛运动规律是______。
A. 、 两个小球相撞
B. 、 两个小球同时落地
C.水平方向做匀速直线运动
D.竖直方向做自由落体运动
(2)小芳利用图2中甲图装置进行实验,每次释放小球的位置都相同,并在乙图的坐标纸上记录了小球经过
的 、 、 三点,已知坐标纸每小格的边长 = 5 ,该小球做平抛运动的初速度大小为______ / ( 取
第 5 页,共 22 页
10 / 2,结果保留2位有效数字)。
(3)小燕在研究平抛运动时发现,若小球下落相同高度,平抛初速度越大,水平射程也越大,依据这一规律,
2 1
她用如图3所示装置来“验证动量守恒定律”:碰撞恢复系数的定义为 = | | ,其中 和 分别是20 10 10 20
碰撞前两小球的速度, 1和 2分别是碰撞后两小球的速度,该实验小球碰撞恢复系数的表达式为 =______(
用题目中字母 、 、 表达),若测得 =______,可以判定小球的碰撞为弹性碰撞。
四、计算题:本大题共 3 小题,共 38 分。
14.一长为 ,质量为 = 3 的木板静止在光滑的水平面上,一质量为 = 1 的滑块以初速度 0 = 4 / 滑
到木板上,木板长度 至少为多少才能使滑块不滑出木板。(滑块与木板间动摩擦因数 = 0.3, 取10 / 2)
15.如图所示,质量均为 的物块 、 用绕过光滑轻质定滑轮的不可伸长的刚性轻绳
连接, 与地面接触, 离地面的高度 为1.2 ,质量为2 的圆环 套在轻绳上, 在
上方 = 0.8 处。由静止释放圆环 , 下落后与 碰撞并粘在一起,碰撞时间极短,
不计 与绳之间的摩擦和空气阻力, 、 、 均可视为质点,重力加速度取10 / 2,
求:
第 6 页,共 22 页
(1) 、 碰撞后瞬间,共同速度为多大;
(2)碰撞后, 经过多长时间到达地面。
16.如图所示,水平地面上放有木板 、 ,木板 的右侧有竖直墙, 板长度为 = 2 ,木板 与地面间的
动摩擦因数为 = 0.1,可视为质点的物块 静置于木板 的左端。不可伸长的轻绳一端系于 点,另一端拴
一小球 ,钉子 位于物块 的正上方, 间距等于绳长的一半, 连线与水平方向的夹角 = 37°,初始
锁定木板 ,将小球 从绳水平拉直的位置由静止释放,到达最低点时与静止的物块 发生碰撞,碰后小球
反弹到达最高点时,轻绳刚好离开钉子 ;物块 滑至木板 右端时,二者共速,且此时木板 与木板 发生
碰撞;碰后木板 恰好能返回初始位置。已知木板 和物块 的质量均为 = 0.3 ,所有碰撞均为弹性碰撞,
物块 与两木板间的动摩擦因数相同,重力加速度大小 = 10 / 2, 37° = 0.6。求:
(1)物块 与木板间的动摩擦因数 ;
(2) 右端到 左端的初始间距为 0;
(3)小球 的质量 ;
(4)若 的右端距墙为0.5 ,现在解除 的锁定,小球 仍由绳水平拉直的位置从静止释放,最终 在 上未
掉下,已知木板 的质量 = 0.9 ,木板 与地面间的摩擦忽略不计, 碰墙后取走 。求木板 的最小长
度 。
第 7 页,共 22 页
答案和解析
1.【答案】
【解析】解: 、小车停在光滑水平面上,车上的人在车上走动时,对人与车组成的系统所受合外力为零,
动量守恒,故 A 错误;
B、子弹水平射入放在光滑水平面上的木块中,对子弹与木块组成的系统所受合外力为零,动量守恒,故 B
错误;
C、子弹射入固定在墙角的木块中,对子弹与木块组成的系统所受合外力不为零,动量不守恒,故 C正确;
D、斜向上抛出的手榴弹在空中炸开时,对手榴弹组成的系统内力远大于外力,动量守恒,故 D 错误;
故选: 。
根据动量守恒定律的条件结合题目选项逐一完成分析。
本题主要考查了动量守恒定律的相关应用,理解动量守恒的条件即可完成分析,难度不大。
2.【答案】
【解析】解:根据题意分析可以知道,木块离开弹簧的瞬间速度大小为 0,方向向右,取向左为正方向,
根据动量定理有
= 0 0 = 2 0,负号代表方向向右;
故 ABD 错误,C正确;
故选: 。
根据动量定理,规定正方向,可求得弹簧对木块的冲量 。
本题考查动量定理,运用过程应注意规定正方向。
3.【答案】
【解析】解:开始阶段, 向右减速, 向左减速,根据系统的动量守恒定律得:当 的速度为零时,设此
时 的速度为 1 .规定向右为正方向,根据动量守恒定律得:
( ) = 1
代入解得: 1 = 2.67 / 。
此后 将向右加速, 继续向左减速;当两者速度达到相同时,设共同速度为 2 .规定向右为正方向,由动
量守恒定律得:
( ) = ( + ) 2,
代入解得: 2 = 2 / 。
第 8 页,共 22 页
两者相对静止后,一起向右做匀速直线运动。
由此可知当 的速度为2.4 / 时, 处于向右加速过程中。故 A 正确,BCD 错误;
故选: 。
分析物体的运动情况:初态时,系统的总动量方向水平向右,两个物体开始均做匀减速运动, 的速度先减
至零,根据动量守恒定律求出此时 的速度.之后, 向右做匀加速运动, 继续向右做匀减速运动,最后
两者一起向右匀速运动.根据动量守恒定律求出薄板的速度大小为2.4 / 时,物块的速度,并分析 的运
动情况.
本题考查应用系统的动量守恒定律分析物体运动情况的能力,这是分析物体运动情况的一种方法,用得较
少,但要学会,比牛顿定律分析物体运动情况简单.
4.【答案】
【解析】解: .水运动至最高点时,速度最小,则此时动量最小,故 A 错误;
√ 2
0 0 45°
B.水在 、 两点的水平分速度相等,则 45° = , 37° = ,得 = = 2 × 3√ 2 / = 5 / ,
37 0.6
故 B 正确;
√ 2
C. 、 两点的竖直分速度分别为 = 45° = 3√ 2 × / = 3 / , = 37° = 5 × 0.8 / =2
2
2 2 4 3
2
4 / ,由 = 2 ,解得 、 两点间的高度差为 = = 0.35 ,故 C错误。 2×10
D.若消防水柱喷水口流速恒定,则任意相等时间内流出水的质量相等,水在空中做匀变速曲线运动,速度
大的地方水柱细,速度小的地方水柱粗,故 D 错误。
故选: 。
A、水运动至最高点时速度最小,则此时动量最小;
B、水在 、 两点的水平分速度相等,根据几何关系列出方程式解答;
C、求出在 、 两点的竖直分速度,运用速度—位移公式解答;
D、水在空中做匀变速曲线运动,速度大的地方水柱细,速度小的地方水柱粗。
考查对动量定理的理解,运动的合成与分解方法的运用,运用方程式解答。
5.【答案】
【解析】解:规定向右为正,设弹丸的质量为4 ,则甲的质量为3 ,乙的质量为 ,炮弹到达最高点时爆
炸时,爆炸的内力远大于重力(外力),遵守动量守恒定律,则有:
4 0 = 3 1 + 2
则8 = 3 1 + 2
第 9 页,共 22 页
2 2×5
两块弹片都做平抛运动,高度一样,则运动时间相等, = √ = √ = 1 ,
10
水平方向做匀速运动, 1 = 1 = 1, 2 = 2 = 2,
则8 = 3 1 + 2
结合图象可知, 的位移满足上述表达式,故 B 正确。
故选: 。
炮弹到达最高点时爆炸时,爆炸的内力远大于重力(外力),遵守动量守恒定律;
当炮弹到达最高点时爆炸为沿水平方向运动的两片,两片炸弹都做平抛运动.根据平抛运动的基本公式即
可解题.
本题考查了动量守恒定律的直接应用,知道当炮弹到达最高点时爆炸为沿水平方向运动的两片,两片炸弹
都做平抛运动,难度适中.
6.【答案】
【解析】解:设飞行器对水的平均作用力为 ,根据牛顿第三定律可知,水对飞行器的作用力大小也为 ,
对运动员与装备由平衡条件得: = = 100 × 10 = 1000
设喷嘴处喷水的速度大小为 ,两个圆管喷嘴的横截面积为 ,在时间 内喷出的水的质量为:
= = 2
取竖直向下为正方向,根据动量定理可得 时间内质量为 的水获得的冲量为:
= + = 2
可得: + 2 = 4 2,当 → 0时,2 → 0,解得:
= √
4
又有: = ( )2,其中 = 10 = 0.1
2
代入数据解得: ≈ 5.6 / ,故 ACD 错误,B 正确。
故选: 。
对运动员与装备由平衡条件求得水对飞行器的作用力大小,根据牛顿第三定律可知飞行器对水的作用力,
根据动量定理求解喷嘴处喷水的速度大小。
本题考查了动量定理的应用,属于流体冲击模型,取一段时间内相互作用的流体为研究对象,应用动量定
理解答。
7.【答案】
第 10 页,共 22 页
【解析】解:物块1与物块2发生弹性碰撞,碰撞过程系统动量守恒、机械能守恒,
以向右为正方向,由动量守恒定律得: 1 0 = 1 1 + 2 2
1 2 1 1由机械能守恒定律得: 1 0 = 1
2 + 2
2 2 1 2 2
2
2
解得: 12 = 1+ 02
物块2与小球3发生弹性碰撞,碰撞过程系统动量守恒、机械能守恒,
以向右为正方向,由动量守恒定律得: 2 2 = 2 2′ + 3 3
1 1 1
由机械能守恒定律得: 22 2 = 2 ′
2
2 +
2
3 3 2 2 2
2 4 4
解得: = 2 2 1 2 0 1 03 = = 2+ 3 ( 1+ )( + ) + +( 1 32 2 3 1 3 + 2) 2
1
设细线的长度为 ,碰撞后小球上升过程机械能守恒,由机械能守恒定律得: 23 3 = 3 (1 ) 2
2
解得: = 1 3 , 是减函数, 越大, 越小,由于 、 一定 3越大 越小,则 越大, 2
当 2 =
1 3,即 2 = √ 1 3时碰撞后小球的速度 3最大,夹角 最大,故 B 正确,ACD 错误。 2
故选: 。
弹性碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律求出碰撞后小球速度,然
后分析判断答题。
本题考查了动量守恒定律的应用,分析清楚运动过程,应用动量守恒定律与机械能守恒定律可以解题。
8.【答案】
【解析】解: 、甲、乙先做加速运动,撤去推力后做减速运动。题图中线段 // ,表明甲、乙两物体
做匀减速运动的加速度相同,依题意,二者质量相等,由牛顿第二定律
=
可知两物体受到的摩擦力大小相等。故 C正确;
、由题图可知,整个运动过程中两物体的始末速度均为零,所以动量改变量均为零,那么合力的冲量
为零: + = 0
可知推力的冲量大小等于物体受到的摩擦力的冲量大小。由题图可知甲的运动时间小于乙的运动时间,所
以摩擦力对甲的冲量小于摩擦力对乙的冲量,则 1的冲量小于 2的冲量,故 AB 错误;D 正确。
故选: 。
由速度图象分析可知,水平推力撤去后, 与 平行,说明加速度相同,动摩擦因数相同,两物体的质量
相等,说明摩擦力大小相等;
第 11 页,共 22 页
根据动量定理,研究整个过程,确定两个推力的冲量关系。
本题首先考查读图能力,其次考查动量定理应用;能够根据全过程动量定理进行求解即可。
9.【答案】
【解析】解: .当 第一次到达左侧最高处时, 、 都有速度,即都有动能,根据系统机械能守恒可知, 第
一次到达左侧最高处时的高度比释放高度低,故 A 错误;
B. 第一次运动到最低点过程中,全程只有重力做功,所以 、 、 构成的系统机械能守恒,故 B 正确;
C. 第一次运动到最低点过程中, 、 一起向右运动,当 第一次到达最低点时, 和 即将分离,则有
= = = 2
第一次运动到最低点过程中,由重力和绳子张力的合力提供向心力,则
( 2 + )
=
第一次运动到最低点过程中, 、 、 构成的系统机械能守恒,则
1 1
2 + 2 × 2 =
2 2
解得
= 4
故 C正确;
D. 第一次运动到最低点过程中, 、 向右运动,此时小球的速度方向与绳子的夹角为钝角,绳子对小球
做负功; 从最低点到左侧最高点过程中, 、 分离, 以原速度做匀速直线运动, 速度减为零后反方向
向左运动,当 、 速度相等时, 球摆到最高点,此过程小球的速度与绳子的夹角先为锐角后为钝角,所
以绳子对小球先做正功再做负功,所以从 开始运动到第一次摆到最高点的过程中,绳子拉力对 先做负功
再做正功最后做负功,故 D 错误。
故选: 。
A.由系统机械能守恒得出结论,且整体机械能守恒,从而进行分析;
B. 第一次运动到最低点过程中, 一起向右运动,当 第一次到达最低点时, 和 即将分离,再根据 做
圆周运动以及 第一次到最低点机械能守恒列式求解;
C.根据圆周运动公式和机械能守恒求 第一次运动到最低点时,绳中张力大小;
D. 第一次运动到最低点过程中, 向右运动,可知此时小球的速度与绳子的夹角为钝角, 从最低点到左
侧最高点过程中, 分离, 以原速度做匀速直线运动, 速度减为零后反方向向左运动,当 速度相等
时, 球摆到最高点,此过程小球的速度与绳子的夹角先为锐角后为钝角。
本题主要是考查机械能守恒定律,主要需熟练掌握整体分析机械能守恒得应用。
第 12 页,共 22 页
10.【答案】
【解析】解: .半圆形槽和小球在水平方向合力为零,水平方向上动量守恒,设小球水平方向分速度大小为
1,槽的速度大小为 2,以向右方向为正方向,则
1 = 3 2
当小球运动到 点时,小球和槽的水平位移最大,设小球的水平位移大小为 1,槽的位移大小为 2,半圆形
槽和小球运动时间相同,则
1 = 3 2
半圆形槽和小球在水平方向上位移大小之和,即相对位移大小为
1 + 2 = 2
解得
2 = 0.5
故 A 错误;
B.若槽固定,小球运动到最低点时速度最大,由机械能守恒
1
2 = 2 2
解得
= 2√
故 B 错误;
C.小球运动 点时,小球和槽在水平方向上速度相同,根据水平方向动量守恒,则此时小球和槽在水平方向
上的速度都为零,根据小球和槽组成的系统机械能守恒,则小球上升的最大高度等于 ,故 C正确;
D.根据功率公式
0 =
可知,当小球在竖直方向分速度最大时,重力的功率最大,设此时小球和 点连线与竖直方向的夹角为 ,
此时速度大小为 ,由动能定理
1
(1 + ) = 2
2
解得
= √ 2 (1 + )
则竖直方向分速度为
= √ 2 (1 + ) = √ 2 (1 + )(1 cos
2 )
第 13 页,共 22 页
1
根据数学求极值的方法可知,当 = 时,竖直方向分速度最大,最大值为
3
8
= √ 3 9
重力做功的最大功率为
=
解得
8
= √ 3 9
故 D 正确。
故选: 。
小球和半圆形槽组成的系统除重力和弹力外不受其他外力,所以整个系统机械能守恒;但是系统在水平方
向上不受任何外力,故水平方向动量守恒。再根据水平动量守恒及整体的机械能守恒进行求解即可。
本题考查了动量与能量的综合应用;解题的关键在于分析小球与半圆形槽组成的系统水平动量守恒,而竖
直方向动量不守恒;整体的机械能守恒。
11.【答案】
【解析】解: .从 = 0开始到 1时刻,取向右为正方向,根据动量守恒定律,有
1 1 = ( 1 + 2) 2
将 1 = 3 / , 2 = 1 / 代入得
1: 2 = 1:2
故 A 正确;
B.从 = 0开始到 0时刻,取向右为正方向,根据动量守恒定律
1 0 = 2 ′2
代入数据解得 2的速度为
3
′2 = / 2
故 B 错误;
C.两物体速度相等时,弹簧的形变量最大,弹性势能最大,但在 = 1 时刻弹簧处于压缩状态,在 = 3 时
刻弹簧处于伸长状态,故 C错误;
D.若考虑两物体从 = 1 到 = 2 的时间内, 2加速运动, 1减速运动,因
1: 2 = 1:2
则在任意时刻两物体的加速度之比为
第 14 页,共 22 页
1: 2 = 2:1
若用微元法考虑,则两物体间的距离
1 1 1 1
= 1 +
2
2 ( 1
2
1 ) =
2
2 + 1
2
2 2 2 2
1
则“ 2
2 2
”对应的位移(面积)为
1 × 1 0.4 = 0.6
1 1
则“ 21 ”对应的位移(面积)为“
2
2 ”对应的位移(面积)的2倍,即为1.2 ,该两部分面积之和与0~1 2 2
内对应的虚线面积相等,如图所示
为1.2 + 0.6 = 1.8 ,即0~1 内弹簧的长度缩短1.8 ,故 D 正确。
故选: 。
从 = 0开始到 1时刻,根据动量守恒定律求解质量之比;从 = 0开始到 0时刻,根据动量守恒定律求解 0时
刻 2的速度;两物体共速的时候,弹簧的形变量最大,弹性势能最大,根据 图像可知判断弹簧处于压
缩还是拉伸状态;根据 图像求解位移,位移之差为弹簧的压缩量。
本题考查动量与量能的综合应用,要求学生能正确分析物体的运动过程,熟练应用对应的规律解题。
+
12.【答案】 1 2 1 2 =
1 2 3
【解析】解:(1)碰撞前, 1落在图中的 ′点,设其水平初速度为 1,小球 1和 2发生碰撞后, 1的落点
在图中 ′点,设其水平初速度为 1′, 2的落点是图中的 ′点,设其水平初速度为 2,设斜面 与水平面
的倾角为 ,
1
由平抛运动规律得 2 =
2, = 1 2
解得: 1 = √ 2 2
同理可得 ′1 = √ , = 2 2 √1 2 3
碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得 1 1 = 1 1′ + 2 2
整理得 1
= 1 + 2
√ 2 √ 3 √ 1
第 15 页,共 22 页
故 A 正确,BCD 错误;
故选: 。
(2)碰撞前, 1落在图中的 点,设其水平初速度为 1 .小球 1和 2发生碰撞后, 1的落点在图中 点,设
其水平初速度为 1 ′, 2的落点是图中的 点,设其水平初速度为 2 .设斜面 与水平面的倾角为 ,
1
由平抛运动规律得: =
2, = 2 1 ,
cos2
解得: 1 = √
2
√ cos
2 cos2
同理可得: 1 ′ = , = √
,
2 2 2
碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得: 1 1 = 1 1′ + 2 2,
整理得: 1√ = 1√ + 2√ ;
故 ABD 错误,C正确;
故选: 。
(3)若让两滑块分别从导轨的左右两侧向中间运动,选取向右为正方向,则有:
1 1 2 2 = ( 1 + 2) 3,
设遮光片的宽度为 ,则: 1 = , 2 = , 3 = , 1 2 3
联立可得: 1
2 + = 1 2
1 2 3
+
故答案为:(1) ;(2) ;(3) 1 2 = 1 2
1 2 3
(1)(2)根据水平方向上的分运动即可验证动量守恒;根据动量守恒定律以及平抛运动规律可确定对应的表达
式。
(3)根据题意应用动量守恒定律求出实验需要验证的表达式。
本题主要考查了动量守恒定律的验证实验,根据实验原理掌握正确的实验操作,结合平抛运动在水平方向
上匀速直线运动的特点完成表达式的分析,同时改进了实验,对学生的要求较高,难度较大。
13.【答案】 1.5 1
【解析】解:(1)该同学观察到的现象是 、 两个小球相撞,说明两球在水平方向的运动完全相同,即反映
平抛运动的规律是水平方向做匀速直线运动,故 AC正确,BD 错误;
故选: 。
2 2×5×10 2
(2)对竖直方向根据公式 = 2,得 = √ = √ = 0.1 ;
10
3 3×5×10 2
对水平方向: 0 = = / = 1.5 / 。 0.1
第 16 页,共 22 页
(3)本实验的原理小球从槽口飞出后作平抛运动的时间相同,设为 ,则有: = 10 , = 1 , = 2 ,
| 2 1 | | | 小球2碰撞前静止,即: 20 = 0,因而碰撞系数为: = = = 。 | 20 10 | |0 |
因为可用小球做平抛运动的水平射程来代替小球抛出时的速度,规定向右为正方向,根据动量守恒有:
1 10 = 1 1 + 2 2
1 1 1
若碰撞过程为弹性碰撞,则机械能守恒,有: 2 2 2
2 1
10 = 1 1 + 2 2 2 2,
整理可得 10 = 2 1
则当 = 1时可以判定小球的碰撞为弹性碰撞。
故答案为:(1) ;(2)1.5;(3) ,1
(1)根据平抛运动的特点判断出实验揭示的规律;
(2)利用平抛运动的公式求初速度;
(3)小球做平抛运动的水平射程来代替小球抛出时的速度,由动量守恒定律和机械能守恒定律求出需要验证
的表达式。
本题考查探究平抛运动规律和验证动量守恒定律,在验证动量守恒定律中,要注意明确实验原理,学会实
验方法;学会在相同高度下,利用平抛运动的水平射程来间接测出速度,并能推导相应的动量守恒表达式
及机械能守恒定律表达式。
14.【答案】解:滑块与木板组成的系统动量守恒,滑块不从木板上滑出,则滑块与木板有相同的末速度,
设末速度大小为 ,滑块与木板的相对位移大小为 。以向右为正方向,对滑块与木板组成的系统由动量守
恒定律得:
0 = ( + )
根据能量守恒定律与功能关系得:
1
= 2
1
0 ( + )
2
2 2
2
联立可得: = 0
2 ( + )
代入数据得: = 2
要使滑块不滑出木板,其长度 至少等于 = 2 。
答:木板长度 至少为2 才能使滑块不滑出木板。
【解析】滑块与木板组成的系统动量守恒,滑块不从木板上滑出,临界条件是滑块与木板共速后,滑块与
木板的相对位移大小恰好等于板长。应用动量守恒定律,结合功能关系解答。
第 17 页,共 22 页
本题考查了动量守恒定律在板块模型中的应用,此题类似于完全非弹性碰撞,损失的机械能转化为摩擦生
热。
15.【答案】解:(1) 与 碰撞前的运动过程,对 ,由机械能守恒定律有
1
2 = × 2 2
2
解得: = 4 /
设 与 碰撞后共同速度为 ,取竖直向下为正方向,以 、 、 组成的系统为研究对象,由动量守恒定律有
2 = ( + + 2 )
解得: = 2 /
(2) 与 碰撞后粘在一起,一起向下做匀加速直线运动,对 、 、 整体,根据牛顿第二定律有
3 = 4
解得: = 2.5 / 2
由运动学公式有
1
= + 2
2
解得碰撞后 到达地面的时间为: = 0.4
答:(1) 、 碰撞后瞬间,共同速度为2 / ;
(2)碰撞后, 经过0.4 时间到达地面。
【解析】(1)对 与 碰撞前的运动过程,根据机械能守恒定律列式,求出 与 碰撞前的速度,根据动量守
恒定律求出碰撞后共同速度大小;
(2) 与 碰撞后粘在一起,根据牛顿第二定律求出加速度,再根据运动学公式求碰撞后 到达地面的时间。
本题是含有非弹性碰撞的类型,要理清物体的运动过程,把握碰撞的基本规律:动量守恒定律。要注意明
确研究对象,采用整体法求连接体的加速度大小,也可以运用隔离法求加速度大小。
16.【答案】解:(1) 在 上滑行时,对 ,有
( + ) = 1
解得
1 = ( 2 )
碰 后,对 ,有
= 2
解得
2 = = 0.1 × 10 /
2 = 1 / 2
第 18 页,共 22 页
木板 锁定, 碰 后恰能返回初始位置,则碰撞前后 的加速度大小相等
1 = 2
解得
= 3 = 3 × 0.1 = 0.3
(2) 在 上滑行时,对 ,有
=
解得
= 3 /
2
在 上滑行的过程中
1 = 1 1
C、 的位移相对关系
1 1
( + ) = 2 共 1 2 共 1
解得 在 上向右滑行的初速度
= 4 /
时间
1 = 1 1内 向前滑行的距离
1
0 = 1
2
1 2
解得
0 = 0.5
(3)小球 下摆过程中
1
( 37° + ) = 2
2 2 2 1
解得
1 = 4√
小球 碰后反弹上摆过程中
1
( 37°) = 2 2 2 2 2
解得
2 = 2√
小球 碰 ,以 1的方向为正方向,根据动量守恒
第 19 页,共 22 页
1 = 2 +
根据能量守恒定律
1
2
1 1
1 =
2 2
2 2 2
+
2
解得
= = 0.1
3
绳长
= 4
(4)解除 锁定后, 、 共速
1 = 1 1
解得
1 = 1 /
方向向右
碰 ,以向右的方向为正方向,对 、 ,根据动量守恒
1 = + 1
根据能量守恒定律
1 1
2 = 2
1
1 +
2
2 2 2 1
解得
1
= / 2
方向向左
1
1 = / 2
方向向右
设 、 达到共同速度 2中, 未碰墙,以向右方向为正方向,根据动量守恒有
1 + 1 = ( + ) 2
解得
5
2 = / , 8
方向向右
设 在 上向右滑过 1,有
第 20 页,共 22 页
1 1 1
=
2 2 2
1 2 1
+
2 1
( + )
2 2
解得
1
1 = 32
此过程中 的对地位移为 1,有
1 1
=
2 2
1 2 2 2 1
解得
9
1 = < 128 0
未碰墙,之后 、 一起匀速运动,碰墙反弹后 、 达到共同速度 3中,以向左为正,根据动量守恒有
2 2 = ( + ) 3
解得
5
3 = / , 16
方向向左
设此过程中 在 上继续向右滑过 2,有
1 1
2 2 2 = ( + ) 2 ( + ) 2 2 3
解得
25
2 = 128
之后 碰 时, 相对 向前滑行,故为了 不掉下, 板的最小长度为
= 1 + 2
解得
29
=
128
答:(1)物块 与木板间的动摩擦因数为0.3;
(2) 右端到 左端的初始间距为为0.5 ;
(3)小球 的质量 为0.1 ;
29
(4)木板 的最小长度 为 。
128
【解析】(1)根据牛顿第二定律求物块 与木板间的动摩擦因数 ;
(2)根据牛顿第二定律和运动学公式求 右端到 左端的初始间距为 0;
(3)根据动量守恒和能量守恒定律求小球 的质量 ;
第 21 页,共 22 页
(4)根据动量守恒和动能定理求木板 的最小长度 。
本题考查受力分析、动能定理、功能关系,物体运动过程中应用动能定理、功能原理解决问题。
第 22 页,共 22 页
同课章节目录
