04 专题4 四边形 2024-2025学年初中数学沪科版八年级下册单元专题练(含答案)
文档属性
| 名称 | 04 专题4 四边形 2024-2025学年初中数学沪科版八年级下册单元专题练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 286.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 20:04:26 | ||
图片预览




文档简介
专题4 四边形
题型归类 举一反三
题型一 多边形的内角与外角
例1 [2023滁州模拟]下列多边形中,内角和是 的是( )
A. B.
C. D.
变式跟进
1.[2023蚌阜模拟]九边形的内角和等于( )
A. B. C. D.
2.[2023滁州模拟]八边形的外角和是( )
A. B. C. D.
3.过多边形的一个顶点可以作2 022条对角线,则这个多边形的边数是( )
A.2 025 B.2 024 C.2 023 D.2 022
题型二 平行四边形的性质和判定
例2 如图,已知垂直平分,,.
(1) 求证:四边形是平行四边形;
(2) 若,,求的长.
变式跟进
4.如图,在四边形中,与相交于点,且,点在上,满足.
(1) 求证:四边形是平行四边形;
(2) 若,,,求四边形的面积.
题型三 矩形的性质和判定
例3 如图,在中,过点作于点,点在上,,连接,.
(1) 求证:四边形是矩形;
(2) 若平分,且,,求矩形的面积.
变式跟进
5.如图,在中,对角线,相交于点,为的中点,连接,的延长线交的延长线于点,连接.
(1) 求证:;
(2) 若, ,判断四边形的形状,并证明你的结论.
题型四 菱形的性质和判定
例4 如图,在中,,,垂足分别为,,且.
(1) 求证:是菱形;
(2) 若,,求的面积.
变式跟进
6.如图,在中, ,是斜边上的中线,是的中点,过点作,交的延长线于点,连接.
(1) 求证:;
(2) 判断四边形的形状,并证明你的结论.
题型五 正方形的性质和判定
例5 [2024潜山模拟]如图,四边形是正方形,为对角线上一点,连接,过点作,交射线于点,以,为邻边作矩形,连接.
(1) 求证:矩形是正方形;
(2) 若,,求的长度;
(3) 当线段与正方形的某条边的夹角是 时,直接写出的度数.
变式跟进
7.如图,在中,,,分别是,的中点,连接并延长交外角的平分线于点.
(1) 求证:;
(2) 连接,,当满足什么条件时,四边形为正方形?请证明你的结论.
题型六 矩形、菱形、正方形的综合
例6 [2024淮北模拟]如图,在中, ,过点的直线,为边上的一点,过点作,垂足为,交直线于点,连接,.
(1) 求证:;
(2) 当为中点时,证明:四边形是菱形;
(3) 在满足(2)的条件下,当满足什么条件时,四边形是正方形?直接写出你的答案.
变式跟进
8.如图,已知是的边的中点,连接并延长,交的延长线于点.
(1) 求证:;
(2) 连接,,若,求证:四边形为矩形;
(3) 在(2)的条件下,当再满足一个什么条件时,四边形为正方形?
题型七 与矩形、菱形、正方形有关的动态型问题
例7 如图,在中, ,, ,点从点出发沿方向以的速度向点匀速运动,同时点从点出发沿方向以的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点,运动的时间是.过点作于点,连接,.
(1) 求证:.
(2) 四边形能够成为菱形吗?如果能,求出相应的值;如果不能,请说明理由.
变式跟进
9.[2024安庆模拟]如图,在四边形中,, ,,,点从点出发,沿线段向点以的速度匀速运动;点从点出发,沿线段向点以的速度匀速运动.已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为.
(1) 如图①,连接,两点,则线段长的取值范围是______________________________.
(2) 当时,求的值.
(3) 如图②,在线段上有一点,,连接和,请问是否存在某一时刻使得平分?若存在,求出的值;若不存在,请说明理由.
过关训练 现复活用
A组·基础达标 逐点击破
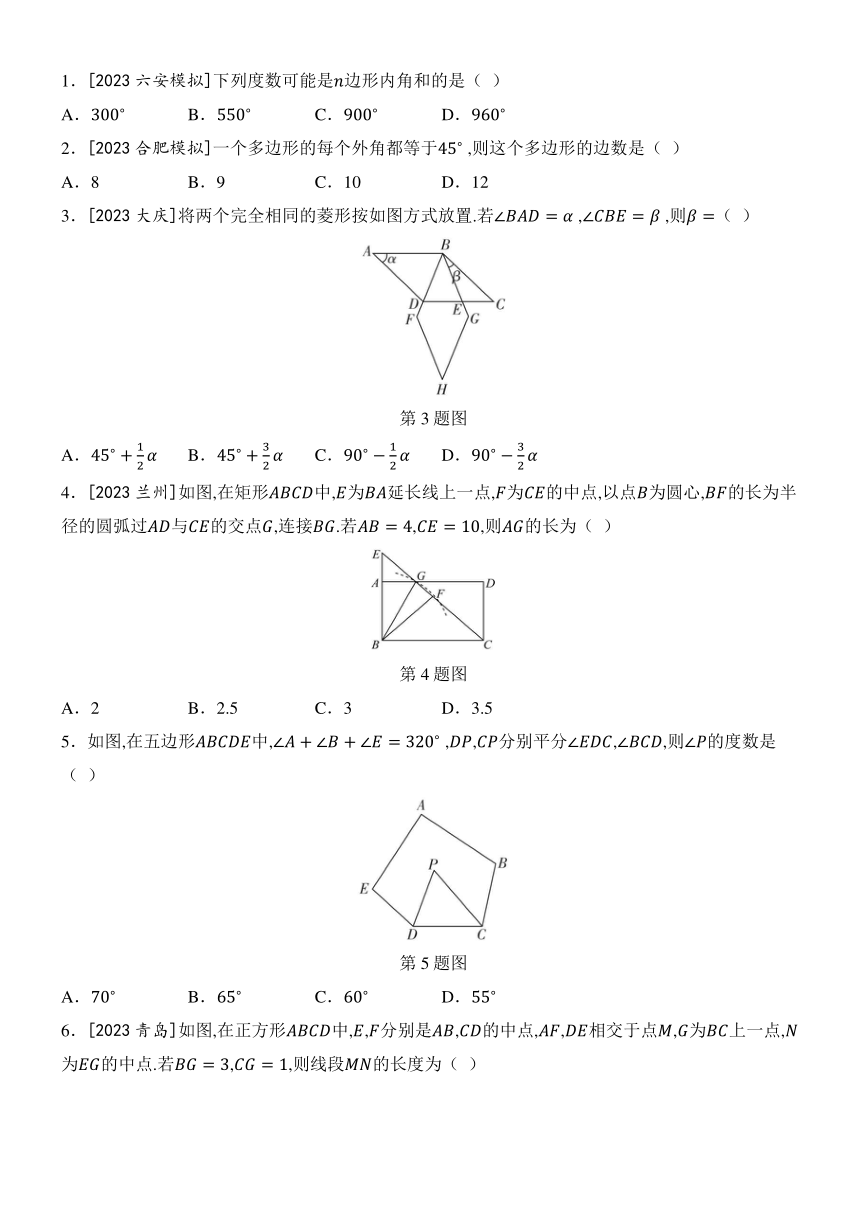
1.[2023六安模拟]下列度数可能是边形内角和的是( )
A. B. C. D.
2.[2023合肥模拟]一个多边形的每个外角都等于 ,则这个多边形的边数是( )
A.8 B.9 C.10 D.12
3.[2023大庆]将两个完全相同的菱形按如图方式放置.若 , ,则( )
第3题图
A. B. C. D.
4.[2023兰州]如图,在矩形中,为延长线上一点,为的中点,以点为圆心,的长为半径的圆弧过与的交点,连接.若,,则的长为( )
第4题图
A.2 B.2.5 C.3 D.3.5
5.如图,在五边形中, ,,分别平分,,则的度数是( )
第5题图
A. B. C. D.
6.[2023青岛]如图,在正方形中,,分别是,的中点,,相交于点,为上一点,为的中点.若,,则线段的长度为( )
第6题图
A. B. C.2 D.
7.如图,将矩形折叠,折痕为,的对应边与交于点.若 ,则的度数为____________.
第7题图
8.[2023牡丹江]如图,在平面直角坐标系中,菱形的顶点,在轴上,,, ,将菱形绕点旋转 后,得到菱形,则点的坐标是______________________________________.
第8题图
9.[2024蚌埠模拟].如图,在中,对角线,交于点,过点且绕该点旋转的动直线分别交线段,于点,(点不与点重合),连接,.
(1) 求证:四边形是平行四边形;
(2) 当四边形是菱形时,,,求的边上的高.
B组·能力提升 强化突破
10.[2023巴中]如图,是等边三角形,,为的中点.以点为圆心,适当长为半径画弧,交于点,交于点,分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.过点作交射线于点,连接,.
(1) 求证:四边形是菱形;
(2) 若,求的面积.
11.[2024宿州模拟]如图,在平面直角坐标系中,的边在轴上,点在轴上.已知, ,,动点从点出发,以每秒2个单位长度的速度向点移动.是的中点,的延长线交于点.
(1) 求点,的坐标;
(2) 当四边形是平行四边形时,求点的移动时间;
(3) 当为等腰三角形时,点的坐标是__________________________________________________.
12.[2024阜阳模拟]问题:如图①,点,分别在正方形的边,上, ,试判断,,之间的数量关系.
【发现证明】 小聪延长至点,使得,得到,从而发现,请你利用图①证明上述结论.
【类比引申】 如图②,在四边形中, ,, ,点,分别在边,上,则当与满足什么数量关系时,仍有?请说明理由.
【探究应用】 如图③,在某公园的同一水平面上,四条通道围成四边形.已知, , , ,道路,上分别有景点,,且,,现要在,之间修一条笔直道路,则这条道路的长为____________(结果取整数.参考数据:,)
专题4 四边形
题型归类 举一反三
题型一 多边形的内角与外角
例1 C
变式跟进
1.B 2.A 3.A
题型二 平行四边形的性质和判定
例2 (1) 证明:垂直平分,
,,
,.
,
.
,
,.
,,,
四边形是平行四边形.
(2) 解: 四边形是平行四边形,,
四边形为菱形,
.
设,则.
,
,
即,解得,
,
.
例2 【点悟】1.证明一个四边形是平行四边形的基本思路:
(1)若已知一组对边平行,可以证明这组对边相等,或另一组对边平行;
(2)若已知一组对边相等,可以证明这组对边平行,或另一组对边相等;
(3)若已知条件与对角线有关,可以证明对角线互相平分.
2.解决与平行四边形的性质有关的问题:
(1)平行四边形具有对边平行且相等、对角相等、对角线互相平分等性质,这为计算边与角、证明三角形全等提供了很多条件,因此,要灵活运用这些性质解题;
(2)在解决平行四边形中的线段和角相等的问题时,常利用平行四边形的性质证明三角形全等来解决.
变式跟进
4.(1) 证明:在和中,
,
.
又,
四边形是平行四边形.
(2) 解:,,
,
是菱形.
,
.
在中,由勾股定理,得
,
,
.
题型三 矩形的性质和判定
例3 (1) 证明: 四边形是平行四边形,
,,
.
,
,
,
四边形是平行四边形.
,
,
四边形是矩形.
(2) 解:,
.
平分,
,
,
.
在中,,,
,
,
.
例3 【点悟】1.证明一个四边形是矩形的基本思路:
(1)若四边形(或可证明)为平行四边形,则再证明一个角是直角或对角线相等;
(2)若直角较多,可证明三个角是直角.
2.利用矩形的性质解题的基本思路:
(1)从对角上看,矩形的四个角都是直角,可将矩形问题转化为直角三角形的问题去解决;
(2)从对角线上看,对角线将矩形分成四个面积相等的等腰三角形,可将矩形问题转化为等腰三角形的问题去解决.
变式跟进
5.(1) 证明: 四边形是平行四边形,
,,.
为的中点,
.
在和中,
,
.
又,.
(2) 解:四边形为矩形.证明如下:
,四边形为平行四边形,
,
.
又,,
,
为等边三角形,
.
,,
四边形为平行四边形,
,.
又,
,
四边形为矩形.
题型四 菱形的性质和判定
例4 (1) 证明: 四边形是平行四边形,
.
,,
.
又,
,
,
是菱形.
(2) 解:如答图,连接,交于点.
例4答图
由(1)知四边形是菱形,,
,.
在中,
,
.
.
例4 【点悟】1.证明一个四边形是菱形的基本思路:
(1)若四边形(或可证)为平行四边形,则再证一组邻边相等或对角线互相垂直;
(2)若相等的边数较多(或容易证出)时,可证明四条边相等.
2.利用菱形的性质解题的基本思路:
(1)菱形的对角线将菱形分成四个全等的直角三角形,可将菱形问题转化为直角三角形的问题去解决;
(2)有一个内角为 (或)的菱形,连接对角线可构成等边三角形,可将菱形问题转化为等边三角形的问题去解决.
变式跟进
6.(1) 证明:,
.
是的中点,
.
在和中,
,
.
(2) 解:四边形是菱形.证明如下:
由(1)知.
是边上的中线,
,
.
,
四边形是平行四边形.
又 ,是的中点,
,
四边形是菱形.
题型五 正方形的性质和判定
例5 (1) 证明:作于点,于,如答图①.
例5答图①
四边形是正方形,
,
又,,
.
, ,
, ,
.
在和中,
,
,
矩形是正方形.
(2) 解:如答图②.
例5答图②
在中,,
,
,
,
点与点重合,此时是等腰直角三角形,易知.
(3) ①当与的夹角为 时, ;
②当与的夹角为 时, .
例5 【点悟】 证明一个四边形是正方形的一般步骤:
(1)先证明它是平行四边形;
(2)再证明有一组邻边相等(或一个角是直角);
(3)最后证明它有一个角是直角(或有一组邻边相等).
变式跟进
7.(1) 证明:,
.
,
.
平分,
.
.
是的中点,
.
在和中,
,
.
(2) 解:当 时,四边形是正方形.
证明:由(1)知,,
,
四边形是平行四边形.
是的中点,,
,
,
四边形是矩形.
,是的中点,
,
四边形是正方形.
题型六 矩形、菱形、正方形的综合
例6 (1) 证明:,
.
,
,
.
,即,
四边形是平行四边形,
.
(2) 证明:为的中点,
.
,
.
又,
四边形是平行四边形.
,为的中点,
,
四边形是菱形.
(3) 解:当 时,四边形是正方形.理由如下:
, ,
.
由(2)可知,四边形是菱形,
,
,
四边形是正方形.
例6 【点悟】 解答特殊平行四边形的结论探究型试题时,要善于根据已知条件和图形,以及由已知条件得出的结论来全面分析,逐步找到所要探究的结论.
变式跟进
8.(1) 证明:在中,,
.
为的中点,
.
在和中,
.
(2) 证明:,
.
,
四边形为平行四边形,
.
,
,
四边形是矩形.
(3) 解:在(2)的条件下,当为等腰三角形,即时,四边形为正方形.理由如下:
由(2)知四边形是矩形.
又,
四边形为正方形.
题型七 与矩形、菱形、正方形有关的动态型问题
例7 (1) 证明: 在中,
, ,
.
,,
且在中, ,
,
.
(2) 解: ,,又,
四边形是平行四边形.
当时,四边形是菱形,
即,解得.
当时,四边形是菱形.
变式跟进
9.(1)
(2) 解:过点作于点,如答图①,则四边形是矩形,
,,
,
,
,,且两点同时出发,当一个点到达终点时,另一点也停止运动,
.
过点作于点,如答图①,
第9题答图①
则四边形是矩形,
,
,
或,
解得或.
(3) 存在某一时刻使得平分.理由如下:
当平分时,四边形是平行四边形,即,如答图②所示.
第9题答图②
,
或,
解得(不合题意,舍去)或,
当的值为6时,平分.
过关训练 现复活用
A组·基础达标 逐点击破
1.C 2.A 3.D 4.C 5.A 6.B
7.
8.或
9.(1) 证明: 四边形是平行四边形,
,,,
.
在和中,
,
.
又,
四边形是平行四边形.
(2) 解:当四边形是菱形时,.
,,
,,
.
设菱形的边上的高为,
则,
即,
解得,
即的边上的高为12.
B组·能力提升 强化突破
10.(1) 证明:是等边三角形,
, .
,
.
为的中点,
.
,
是等边三角形.
.
由作图知,平分,
.
,,
,.
又,
四边形是平行四边形.
,
四边形是菱形.
(2) 解:是等边三角形,,
, , .
,,
.
四边形是菱形,
,.
在中, ,
,.
.
.
11.(1) 解:, ,,
,.
在中,由勾股定理,得
.
,,
,
.
四边形是平行四边形,
,
点的坐标为,点的坐标为.
(2) 四边形是平行四边形,
.
.
是的中点,
是的中位线,
是的中点,
,
,
解得,
故点移动的时间为.
(3) 或或
12.【发现证明】 证明:,
,,.
四边形是正方形, ,
, ,
,
.
在和中,
,
,
.
又,,
,
.
【类比引申】 解:当时,仍有.理由如下:
如答图,延长至点,使,连接.
第12题答图
, ,
.
在和中,
,
,.
,
,
.
在和中,
,
,
,
即.
【探究应用】
题型归类 举一反三
题型一 多边形的内角与外角
例1 [2023滁州模拟]下列多边形中,内角和是 的是( )
A. B.
C. D.
变式跟进
1.[2023蚌阜模拟]九边形的内角和等于( )
A. B. C. D.
2.[2023滁州模拟]八边形的外角和是( )
A. B. C. D.
3.过多边形的一个顶点可以作2 022条对角线,则这个多边形的边数是( )
A.2 025 B.2 024 C.2 023 D.2 022
题型二 平行四边形的性质和判定
例2 如图,已知垂直平分,,.
(1) 求证:四边形是平行四边形;
(2) 若,,求的长.
变式跟进
4.如图,在四边形中,与相交于点,且,点在上,满足.
(1) 求证:四边形是平行四边形;
(2) 若,,,求四边形的面积.
题型三 矩形的性质和判定
例3 如图,在中,过点作于点,点在上,,连接,.
(1) 求证:四边形是矩形;
(2) 若平分,且,,求矩形的面积.
变式跟进
5.如图,在中,对角线,相交于点,为的中点,连接,的延长线交的延长线于点,连接.
(1) 求证:;
(2) 若, ,判断四边形的形状,并证明你的结论.
题型四 菱形的性质和判定
例4 如图,在中,,,垂足分别为,,且.
(1) 求证:是菱形;
(2) 若,,求的面积.
变式跟进
6.如图,在中, ,是斜边上的中线,是的中点,过点作,交的延长线于点,连接.
(1) 求证:;
(2) 判断四边形的形状,并证明你的结论.
题型五 正方形的性质和判定
例5 [2024潜山模拟]如图,四边形是正方形,为对角线上一点,连接,过点作,交射线于点,以,为邻边作矩形,连接.
(1) 求证:矩形是正方形;
(2) 若,,求的长度;
(3) 当线段与正方形的某条边的夹角是 时,直接写出的度数.
变式跟进
7.如图,在中,,,分别是,的中点,连接并延长交外角的平分线于点.
(1) 求证:;
(2) 连接,,当满足什么条件时,四边形为正方形?请证明你的结论.
题型六 矩形、菱形、正方形的综合
例6 [2024淮北模拟]如图,在中, ,过点的直线,为边上的一点,过点作,垂足为,交直线于点,连接,.
(1) 求证:;
(2) 当为中点时,证明:四边形是菱形;
(3) 在满足(2)的条件下,当满足什么条件时,四边形是正方形?直接写出你的答案.
变式跟进
8.如图,已知是的边的中点,连接并延长,交的延长线于点.
(1) 求证:;
(2) 连接,,若,求证:四边形为矩形;
(3) 在(2)的条件下,当再满足一个什么条件时,四边形为正方形?
题型七 与矩形、菱形、正方形有关的动态型问题
例7 如图,在中, ,, ,点从点出发沿方向以的速度向点匀速运动,同时点从点出发沿方向以的速度向点匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点,运动的时间是.过点作于点,连接,.
(1) 求证:.
(2) 四边形能够成为菱形吗?如果能,求出相应的值;如果不能,请说明理由.
变式跟进
9.[2024安庆模拟]如图,在四边形中,, ,,,点从点出发,沿线段向点以的速度匀速运动;点从点出发,沿线段向点以的速度匀速运动.已知两点同时出发,当一个点到达终点时,另一点也停止运动,设运动时间为.
(1) 如图①,连接,两点,则线段长的取值范围是______________________________.
(2) 当时,求的值.
(3) 如图②,在线段上有一点,,连接和,请问是否存在某一时刻使得平分?若存在,求出的值;若不存在,请说明理由.
过关训练 现复活用
A组·基础达标 逐点击破
1.[2023六安模拟]下列度数可能是边形内角和的是( )
A. B. C. D.
2.[2023合肥模拟]一个多边形的每个外角都等于 ,则这个多边形的边数是( )
A.8 B.9 C.10 D.12
3.[2023大庆]将两个完全相同的菱形按如图方式放置.若 , ,则( )
第3题图
A. B. C. D.
4.[2023兰州]如图,在矩形中,为延长线上一点,为的中点,以点为圆心,的长为半径的圆弧过与的交点,连接.若,,则的长为( )
第4题图
A.2 B.2.5 C.3 D.3.5
5.如图,在五边形中, ,,分别平分,,则的度数是( )
第5题图
A. B. C. D.
6.[2023青岛]如图,在正方形中,,分别是,的中点,,相交于点,为上一点,为的中点.若,,则线段的长度为( )
第6题图
A. B. C.2 D.
7.如图,将矩形折叠,折痕为,的对应边与交于点.若 ,则的度数为____________.
第7题图
8.[2023牡丹江]如图,在平面直角坐标系中,菱形的顶点,在轴上,,, ,将菱形绕点旋转 后,得到菱形,则点的坐标是______________________________________.
第8题图
9.[2024蚌埠模拟].如图,在中,对角线,交于点,过点且绕该点旋转的动直线分别交线段,于点,(点不与点重合),连接,.
(1) 求证:四边形是平行四边形;
(2) 当四边形是菱形时,,,求的边上的高.
B组·能力提升 强化突破
10.[2023巴中]如图,是等边三角形,,为的中点.以点为圆心,适当长为半径画弧,交于点,交于点,分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.过点作交射线于点,连接,.
(1) 求证:四边形是菱形;
(2) 若,求的面积.
11.[2024宿州模拟]如图,在平面直角坐标系中,的边在轴上,点在轴上.已知, ,,动点从点出发,以每秒2个单位长度的速度向点移动.是的中点,的延长线交于点.
(1) 求点,的坐标;
(2) 当四边形是平行四边形时,求点的移动时间;
(3) 当为等腰三角形时,点的坐标是__________________________________________________.
12.[2024阜阳模拟]问题:如图①,点,分别在正方形的边,上, ,试判断,,之间的数量关系.
【发现证明】 小聪延长至点,使得,得到,从而发现,请你利用图①证明上述结论.
【类比引申】 如图②,在四边形中, ,, ,点,分别在边,上,则当与满足什么数量关系时,仍有?请说明理由.
【探究应用】 如图③,在某公园的同一水平面上,四条通道围成四边形.已知, , , ,道路,上分别有景点,,且,,现要在,之间修一条笔直道路,则这条道路的长为____________(结果取整数.参考数据:,)
专题4 四边形
题型归类 举一反三
题型一 多边形的内角与外角
例1 C
变式跟进
1.B 2.A 3.A
题型二 平行四边形的性质和判定
例2 (1) 证明:垂直平分,
,,
,.
,
.
,
,.
,,,
四边形是平行四边形.
(2) 解: 四边形是平行四边形,,
四边形为菱形,
.
设,则.
,
,
即,解得,
,
.
例2 【点悟】1.证明一个四边形是平行四边形的基本思路:
(1)若已知一组对边平行,可以证明这组对边相等,或另一组对边平行;
(2)若已知一组对边相等,可以证明这组对边平行,或另一组对边相等;
(3)若已知条件与对角线有关,可以证明对角线互相平分.
2.解决与平行四边形的性质有关的问题:
(1)平行四边形具有对边平行且相等、对角相等、对角线互相平分等性质,这为计算边与角、证明三角形全等提供了很多条件,因此,要灵活运用这些性质解题;
(2)在解决平行四边形中的线段和角相等的问题时,常利用平行四边形的性质证明三角形全等来解决.
变式跟进
4.(1) 证明:在和中,
,
.
又,
四边形是平行四边形.
(2) 解:,,
,
是菱形.
,
.
在中,由勾股定理,得
,
,
.
题型三 矩形的性质和判定
例3 (1) 证明: 四边形是平行四边形,
,,
.
,
,
,
四边形是平行四边形.
,
,
四边形是矩形.
(2) 解:,
.
平分,
,
,
.
在中,,,
,
,
.
例3 【点悟】1.证明一个四边形是矩形的基本思路:
(1)若四边形(或可证明)为平行四边形,则再证明一个角是直角或对角线相等;
(2)若直角较多,可证明三个角是直角.
2.利用矩形的性质解题的基本思路:
(1)从对角上看,矩形的四个角都是直角,可将矩形问题转化为直角三角形的问题去解决;
(2)从对角线上看,对角线将矩形分成四个面积相等的等腰三角形,可将矩形问题转化为等腰三角形的问题去解决.
变式跟进
5.(1) 证明: 四边形是平行四边形,
,,.
为的中点,
.
在和中,
,
.
又,.
(2) 解:四边形为矩形.证明如下:
,四边形为平行四边形,
,
.
又,,
,
为等边三角形,
.
,,
四边形为平行四边形,
,.
又,
,
四边形为矩形.
题型四 菱形的性质和判定
例4 (1) 证明: 四边形是平行四边形,
.
,,
.
又,
,
,
是菱形.
(2) 解:如答图,连接,交于点.
例4答图
由(1)知四边形是菱形,,
,.
在中,
,
.
.
例4 【点悟】1.证明一个四边形是菱形的基本思路:
(1)若四边形(或可证)为平行四边形,则再证一组邻边相等或对角线互相垂直;
(2)若相等的边数较多(或容易证出)时,可证明四条边相等.
2.利用菱形的性质解题的基本思路:
(1)菱形的对角线将菱形分成四个全等的直角三角形,可将菱形问题转化为直角三角形的问题去解决;
(2)有一个内角为 (或)的菱形,连接对角线可构成等边三角形,可将菱形问题转化为等边三角形的问题去解决.
变式跟进
6.(1) 证明:,
.
是的中点,
.
在和中,
,
.
(2) 解:四边形是菱形.证明如下:
由(1)知.
是边上的中线,
,
.
,
四边形是平行四边形.
又 ,是的中点,
,
四边形是菱形.
题型五 正方形的性质和判定
例5 (1) 证明:作于点,于,如答图①.
例5答图①
四边形是正方形,
,
又,,
.
, ,
, ,
.
在和中,
,
,
矩形是正方形.
(2) 解:如答图②.
例5答图②
在中,,
,
,
,
点与点重合,此时是等腰直角三角形,易知.
(3) ①当与的夹角为 时, ;
②当与的夹角为 时, .
例5 【点悟】 证明一个四边形是正方形的一般步骤:
(1)先证明它是平行四边形;
(2)再证明有一组邻边相等(或一个角是直角);
(3)最后证明它有一个角是直角(或有一组邻边相等).
变式跟进
7.(1) 证明:,
.
,
.
平分,
.
.
是的中点,
.
在和中,
,
.
(2) 解:当 时,四边形是正方形.
证明:由(1)知,,
,
四边形是平行四边形.
是的中点,,
,
,
四边形是矩形.
,是的中点,
,
四边形是正方形.
题型六 矩形、菱形、正方形的综合
例6 (1) 证明:,
.
,
,
.
,即,
四边形是平行四边形,
.
(2) 证明:为的中点,
.
,
.
又,
四边形是平行四边形.
,为的中点,
,
四边形是菱形.
(3) 解:当 时,四边形是正方形.理由如下:
, ,
.
由(2)可知,四边形是菱形,
,
,
四边形是正方形.
例6 【点悟】 解答特殊平行四边形的结论探究型试题时,要善于根据已知条件和图形,以及由已知条件得出的结论来全面分析,逐步找到所要探究的结论.
变式跟进
8.(1) 证明:在中,,
.
为的中点,
.
在和中,
.
(2) 证明:,
.
,
四边形为平行四边形,
.
,
,
四边形是矩形.
(3) 解:在(2)的条件下,当为等腰三角形,即时,四边形为正方形.理由如下:
由(2)知四边形是矩形.
又,
四边形为正方形.
题型七 与矩形、菱形、正方形有关的动态型问题
例7 (1) 证明: 在中,
, ,
.
,,
且在中, ,
,
.
(2) 解: ,,又,
四边形是平行四边形.
当时,四边形是菱形,
即,解得.
当时,四边形是菱形.
变式跟进
9.(1)
(2) 解:过点作于点,如答图①,则四边形是矩形,
,,
,
,
,,且两点同时出发,当一个点到达终点时,另一点也停止运动,
.
过点作于点,如答图①,
第9题答图①
则四边形是矩形,
,
,
或,
解得或.
(3) 存在某一时刻使得平分.理由如下:
当平分时,四边形是平行四边形,即,如答图②所示.
第9题答图②
,
或,
解得(不合题意,舍去)或,
当的值为6时,平分.
过关训练 现复活用
A组·基础达标 逐点击破
1.C 2.A 3.D 4.C 5.A 6.B
7.
8.或
9.(1) 证明: 四边形是平行四边形,
,,,
.
在和中,
,
.
又,
四边形是平行四边形.
(2) 解:当四边形是菱形时,.
,,
,,
.
设菱形的边上的高为,
则,
即,
解得,
即的边上的高为12.
B组·能力提升 强化突破
10.(1) 证明:是等边三角形,
, .
,
.
为的中点,
.
,
是等边三角形.
.
由作图知,平分,
.
,,
,.
又,
四边形是平行四边形.
,
四边形是菱形.
(2) 解:是等边三角形,,
, , .
,,
.
四边形是菱形,
,.
在中, ,
,.
.
.
11.(1) 解:, ,,
,.
在中,由勾股定理,得
.
,,
,
.
四边形是平行四边形,
,
点的坐标为,点的坐标为.
(2) 四边形是平行四边形,
.
.
是的中点,
是的中位线,
是的中点,
,
,
解得,
故点移动的时间为.
(3) 或或
12.【发现证明】 证明:,
,,.
四边形是正方形, ,
, ,
,
.
在和中,
,
,
.
又,,
,
.
【类比引申】 解:当时,仍有.理由如下:
如答图,延长至点,使,连接.
第12题答图
, ,
.
在和中,
,
,.
,
,
.
在和中,
,
,
,
即.
【探究应用】
