05 专题5 数据的初步分析(含答案) 2024-2025学年初中数学沪科版八年级下册单元专题练
文档属性
| 名称 | 05 专题5 数据的初步分析(含答案) 2024-2025学年初中数学沪科版八年级下册单元专题练 |  | |
| 格式 | docx | ||
| 文件大小 | 154.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 19:48:10 | ||
图片预览




文档简介
专题5 数据的初步分析
题型归类 举一反三
题型一 频数与频率
例1 [2023安庆模拟]一个样本含有20个数据:68,69,70,66,68,64,65,65,69,62,67,66,65,67,63,65,64,61,65,66,在列频数分布表时,这组的频数为( )
A.5 B.6 C.7 D.8
变式跟进
1.[2023滁州模拟]有40个数据,共分成6组,第组的频数分别为10,4,4,6,第5组的频率是,则6组的频率是____________.
2.[2024淮南模拟]数学小组为了了解该校学生对食堂就餐的评价,抽取部分学生参加问卷评价调查,整理并制作出如下的统计表和统计图:
组别 评价得分 频数 频率
A 30 0.1
B 90
C 0.4
D 60 0.2
根据以上信息,解答下列问题:
(1) 本次问卷评价调查共抽取____________名学生参加;
(2) 补全频数直方图;
(3) 若全校共1 200名学生,试估计评价得分不低于80分的学生有____________名.
题型二 平均数、中位数、众数
例2 在一次数学考试中,某小组的10名学生的成绩如下表:
分数 60 70 80 90 100
人数 1 1 5 2 1
则下列说法正确的是( )
A.学生成绩是80分的频率是 B.学生成绩的中位数是80分
C.学生成绩的众数是5 D.学生成绩的平均数是80分
变式跟进
3.某校要在甲、乙两名学生中选择一人参加市级的演讲比赛,对他们的演讲材料、语言表达、形体语言三方面进行测评,根据综合成绩择优去参加比赛.他们的各项成绩(单项满分100分)如下表:
候选人 演讲材料 语言表达 形体语言
甲 93分 87分 83分
乙 88分 96分 80分
(1) 如果把各项成绩的平均数作为综合成绩,应该让谁参加比赛?
(2) 如果想让一名综合能力较强的同学参加比赛,把演讲材料、语言表达、形体语言三方面成绩分别按照,,的比例计入综合成绩,应该让谁参加比赛?
4.[2024淮南模拟]《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,某中学开展“朗读”比赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1) 根据图示填写下表:
班级 平均数 中位数 众数
八(1)班 85 __________ 85
八(2)班 __________ 80 ____________
(2) 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
题型三 方差
例3 市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表:
选手 测试成绩/环 中位数 平均数
甲 10 9 8 8 10 9 ____ ____
乙 10 10 8 10 7 ____ 9.5 9
(1) 把表格中的数据填写完整;
(2) 分别计算甲、乙六次测试成绩的方差;
(3) 根据(1),(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
变式跟进
5.某企业复工之后,举行了一个简单的技工比赛,参赛的五名选手在单位时间内加工零件的合格率分别为:,,,,.关于这组数据,下列说法正确的是( )
A.平均数是 B.方差是0
C.中位数是 D.众数是
6.若一组数据2,3,4,5,的方差比另一组数据5,6,7,8,9的方差大,则的值可能是( )
A.1 B.4 C.6 D.8
题型四 用样本估计总体
例4 [2023合肥模拟]为了加强对青少年防溺水安全教育,4月初某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):
87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
【整理数据】
成绩/分 86 87 89 91 95 96 97 99 100
学生 人数 2 2 2 4 1 3 3 2 1
【分析数据】
平均数 众数 中位数
93
根据以上信息,解答下列问题:
(1) 填空:__________,__________;
(2) 若成绩达到95分及以上为“优秀”等级,则“优秀”等级所占的百分率为____________;
(3) 请估计该校1 500名学生中成绩达到95分及以上的学生人数.
变式跟进
7.[2024蚌埠模拟]为了解八年级各班男生引体向上情况,随机抽取八(1)班、八(2)班各5名男生进行测试,其有效次数分别为:
八(1)班:7,10,8,10,10;
八(2)班:9,9,8,9,10.
在不考虑其他因素的情况下,规定男生引体向上有效次数10次的成绩为满分.现从平均数、众数、中位数、方差四个统计量对两个班男生的测试数据做如下分析:
组别 平均数 众数 中位数 方差
八(1)班 9 9
八(2)班 9 0.4
根据以上信息,解答下列问题:
(1) 填空:________,__________,________,____________;
(2) 请从众数和方差两个方面对八(1)、 八(2)两班男生引体向上的成绩作出评价;
(3) 以这10名男生的成绩为样本,估计八年级300名男生引体向上成绩达到满分的男生有____________名.
题型五 分析数据进行决策
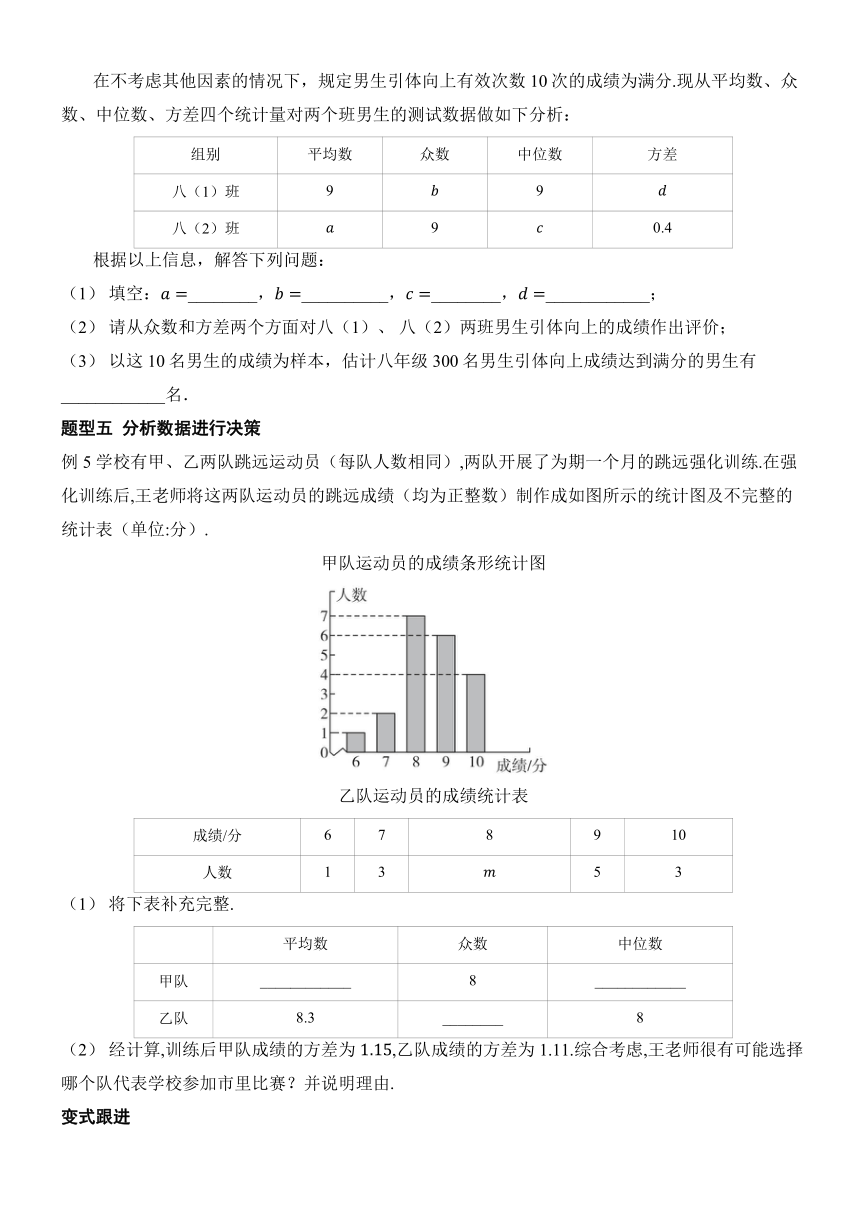
例5 学校有甲、乙两队跳远运动员(每队人数相同),两队开展了为期一个月的跳远强化训练.在强化训练后,王老师将这两队运动员的跳远成绩(均为正整数)制作成如图所示的统计图及不完整的统计表(单位:分).
甲队运动员的成绩条形统计图
乙队运动员的成绩统计表
成绩/分 6 7 8 9 10
人数 1 3 5 3
(1) 将下表补充完整.
平均数 众数 中位数
甲队 ____________ 8 ____________
乙队 8.3 ________ 8
(2) 经计算,训练后甲队成绩的方差为,乙队成绩的方差为1.11.综合考虑,王老师很有可能选择哪个队代表学校参加市里比赛?并说明理由.
变式跟进
8.某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数.数据如下:
20 21 19 16 27 18 31 29 21 22
25 20 19 22 35 33 19 17 18 29
18 35 22 15 18 18 31 31 19 22
整理上面的数据,得到如下条形统计图.
样本数据的平均数、众数、中位数如下表所示:
统计量 平均数 众数 中位数
数值 23 21
根据以上信息,解答下列问题:
(1) 上表中众数的值为__________;
(2) 为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获得奖励,应根据________来确定奖励标准比较合适(填“平均数”“众数”或“中位数”);
(3) 该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
过关训练 现复活用
A组·基础达标 逐点击破
1.小明调查了某地1月份一周的最低气温(单位: ),分别是,0,3,,1,0,2,其中以上(不含)出现的频数是( )
A.2 B.3 C.4 D.5
2.[2022自贡]六名同学的年龄(岁)分别是:13,14,15,14,14,15.关于这组数据,正确的说法是( )
A.平均数是14 B.中位数是14.5
C.方差是3 D.众数是14
3.某校四个绿化小组一天植树的棵数分别为9,9,,7,已知这组数据的众数和平均数相等,那么这组数据的中位数是( )
A.8 B.9 C.10 D.12
4.若一组数据,, ,的平均数为5,方差为9,则数据,, ,的平均数为____________,方差为__________.
5.某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科技能力,开展了“最强大脑”邀请赛.现从七、八年级中各随机抽取了20名学生的初赛成绩(初赛成绩均为整数,满分为10分,9分及以上为优秀)统计、整理如下:
七年级抽取的学生的初赛成绩:
6,6,7,7,7,8,8,8,8,8,9,9,9,9,9,9,9,10,10,10.
七、八年级抽取的学生的初赛成绩统计表
年级 平均数 中位数 众数 方差 优秀率
七年级 8.3 8.5 1.41
八年级 8.3 8 7 1.61
根据以上信息,解答下列问题:
(1) 填空:________,__________.
(2) 若该校八年级有900名学生参加初赛,规定满分才可进入复赛,估计八年级进入复赛的学生有____________名.
(3) 根据以上数据,你认为七、八年级学生在“最强大脑”邀请赛中,哪个年级的学生初赛成绩更好?请说明理由(写出一条理由即可).
B组·能力提升 强化突破
6.[2024六安模拟]甲,乙两个小区各有300户居民,为了解这两个小区3月份用户使用燃气量情况,小明和小丽分别从中随机抽取30户进行调查,并对数据进行整理、描述和分析.下面给出了部分信息.
.甲小区用气量频数分布表如下:
分组
频数 3 6 10 3
.乙小区用气量频数直方图如下(数据分成5组:,,,,):
.乙小区用气量的数据在这一组的是:15,15,16,16,16,17,17,18,18,18,18,19
.甲,乙两小区用气量的平均数、中位数、众数如下表:
小区 平均数 中位数 众数
甲 17.4 18 13
乙 17.1 18
根据以上信息,解答下列问题:
(1) 填空:________,____________;
(2) 在甲小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.在乙小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.比较,的大小,并说明理由;
(3) 估计甲、乙两小区中用气量不小于的总户数为____________户.
专题5 数据的初步分析
题型归类 举一反三
题型一 频数与频率
例1 D
变式跟进
1.
2.(1)
(2) 解:C组频数为,补全频数直方图略.
(3)
题型二 平均数、中位数、众数
例2 B
【点悟】 找中位数要把数据按大小顺序排列,位于最中间的一个数(数据总数为奇数)或两个数的平均数(数据总数为偶数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数为所有数据的和除以数据的个数.
变式跟进
3.(1) 解:甲的平均分为(分),
乙的平均分为(分).
,
乙的综合成绩比甲的高,
应该让乙参加比赛.
(2) 甲的综合成绩为(分),
乙的综合成绩为(分).
, 应该让甲参加比赛.
4.(1) ; ;
(2) 解:八(1)班的复赛成绩较好,理由如下:
两个班级成绩的平均数相同,八(1)班的中位数高,
在平均数相同的情况下,中位数高的八(1)班的复赛成绩较好(答案不唯一).
题型三 方差
例3 (1) 9; 9; 9
(2) 解:;
.
(3) (答案不唯一,合理即可)我认为推荐甲参加省比赛更合适.理由如下:
两人的平均成绩相等,说明实力相当,但甲的六次测试成绩的方差比乙小,说明甲的发挥较为稳定,故推荐甲参加省比赛更合适.
例3 【点悟】 计算方差:“先平均、再作差、平方后、再平均”,也就是说,先求出一组数据的平均数,再将每一个数据都与平均数作差,然后将这些差进行平方,最后求这些差的平方的平均数,其结果就是这组数据的方差.
变式跟进
5.D 6.D
题型四 用样本估计总体
例4 (1) ;
(2)
(3) 解:估计该校1 500名学生中成绩达到95分及以上的学生有(名).
例4 【点悟】 用样本估计总体是统计的核心思想.具体的有用样本平均数估计总体平均数、用样本百分率估计总体百分率、用样本方差估计总体方差等.
变式跟进
7.(1) ; ; ;
(2) 解:八(1)班的众数为10,大于八(2)班的众数,因此八(1)班成绩达到满分的人数较多,满分率较高;八(2)班的方差小于八(1)班的方差,因此八(2)班的成绩比较稳定.
(3)
题型五 分析数据进行决策
例5 (1) ; ;
(2) 解:王老师很有可能会选择甲队作为学校代表参加市里比赛.理由如下:
甲、乙两队的方差相差不大,说明两队成绩整齐程度不相上下,但甲队的平均成绩较高,且甲队10分有4人,9分有6人,均比乙队多,
王老师很有可能会选择甲队作为学校代表参加市里比赛.
例5 【点悟】 分析数据进行决策时,关键在于确定决策侧重的方面,从而可以从平均数、中位数、众数、方差等不同角度出发,衡量各种选择的优劣.
变式跟进
8.(1)
(2) 中位数
(3) 解:(名).
答:估计该部门生产能手的人数为100.
过关训练 现复活用
A组·基础达标 逐点击破
1.B 2.D 3.B
4.;
5.(1) ;
(2)
(3) 解:(答案不唯一,合理即可)根据题意可知,七、八年级的优秀率分别是,,
故七年级的学生初赛成绩更好.
B组·能力提升 强化突破
6.(1) ;
(2) 解:,理由如下:
甲小区的中位数高于平均数,则至少为15户;乙小区高于平均数的户数(户),
.
(3)
题型归类 举一反三
题型一 频数与频率
例1 [2023安庆模拟]一个样本含有20个数据:68,69,70,66,68,64,65,65,69,62,67,66,65,67,63,65,64,61,65,66,在列频数分布表时,这组的频数为( )
A.5 B.6 C.7 D.8
变式跟进
1.[2023滁州模拟]有40个数据,共分成6组,第组的频数分别为10,4,4,6,第5组的频率是,则6组的频率是____________.
2.[2024淮南模拟]数学小组为了了解该校学生对食堂就餐的评价,抽取部分学生参加问卷评价调查,整理并制作出如下的统计表和统计图:
组别 评价得分 频数 频率
A 30 0.1
B 90
C 0.4
D 60 0.2
根据以上信息,解答下列问题:
(1) 本次问卷评价调查共抽取____________名学生参加;
(2) 补全频数直方图;
(3) 若全校共1 200名学生,试估计评价得分不低于80分的学生有____________名.
题型二 平均数、中位数、众数
例2 在一次数学考试中,某小组的10名学生的成绩如下表:
分数 60 70 80 90 100
人数 1 1 5 2 1
则下列说法正确的是( )
A.学生成绩是80分的频率是 B.学生成绩的中位数是80分
C.学生成绩的众数是5 D.学生成绩的平均数是80分
变式跟进
3.某校要在甲、乙两名学生中选择一人参加市级的演讲比赛,对他们的演讲材料、语言表达、形体语言三方面进行测评,根据综合成绩择优去参加比赛.他们的各项成绩(单项满分100分)如下表:
候选人 演讲材料 语言表达 形体语言
甲 93分 87分 83分
乙 88分 96分 80分
(1) 如果把各项成绩的平均数作为综合成绩,应该让谁参加比赛?
(2) 如果想让一名综合能力较强的同学参加比赛,把演讲材料、语言表达、形体语言三方面成绩分别按照,,的比例计入综合成绩,应该让谁参加比赛?
4.[2024淮南模拟]《朗读者》自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,某中学开展“朗读”比赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1) 根据图示填写下表:
班级 平均数 中位数 众数
八(1)班 85 __________ 85
八(2)班 __________ 80 ____________
(2) 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
题型三 方差
例3 市射击队为从甲、乙两名运动员中选拔一人参加省比赛,对他们进行了六次测试,测试成绩如下表:
选手 测试成绩/环 中位数 平均数
甲 10 9 8 8 10 9 ____ ____
乙 10 10 8 10 7 ____ 9.5 9
(1) 把表格中的数据填写完整;
(2) 分别计算甲、乙六次测试成绩的方差;
(3) 根据(1),(2)计算的结果,你认为推荐谁参加省比赛更合适?请说明理由.
变式跟进
5.某企业复工之后,举行了一个简单的技工比赛,参赛的五名选手在单位时间内加工零件的合格率分别为:,,,,.关于这组数据,下列说法正确的是( )
A.平均数是 B.方差是0
C.中位数是 D.众数是
6.若一组数据2,3,4,5,的方差比另一组数据5,6,7,8,9的方差大,则的值可能是( )
A.1 B.4 C.6 D.8
题型四 用样本估计总体
例4 [2023合肥模拟]为了加强对青少年防溺水安全教育,4月初某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):
87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
【整理数据】
成绩/分 86 87 89 91 95 96 97 99 100
学生 人数 2 2 2 4 1 3 3 2 1
【分析数据】
平均数 众数 中位数
93
根据以上信息,解答下列问题:
(1) 填空:__________,__________;
(2) 若成绩达到95分及以上为“优秀”等级,则“优秀”等级所占的百分率为____________;
(3) 请估计该校1 500名学生中成绩达到95分及以上的学生人数.
变式跟进
7.[2024蚌埠模拟]为了解八年级各班男生引体向上情况,随机抽取八(1)班、八(2)班各5名男生进行测试,其有效次数分别为:
八(1)班:7,10,8,10,10;
八(2)班:9,9,8,9,10.
在不考虑其他因素的情况下,规定男生引体向上有效次数10次的成绩为满分.现从平均数、众数、中位数、方差四个统计量对两个班男生的测试数据做如下分析:
组别 平均数 众数 中位数 方差
八(1)班 9 9
八(2)班 9 0.4
根据以上信息,解答下列问题:
(1) 填空:________,__________,________,____________;
(2) 请从众数和方差两个方面对八(1)、 八(2)两班男生引体向上的成绩作出评价;
(3) 以这10名男生的成绩为样本,估计八年级300名男生引体向上成绩达到满分的男生有____________名.
题型五 分析数据进行决策
例5 学校有甲、乙两队跳远运动员(每队人数相同),两队开展了为期一个月的跳远强化训练.在强化训练后,王老师将这两队运动员的跳远成绩(均为正整数)制作成如图所示的统计图及不完整的统计表(单位:分).
甲队运动员的成绩条形统计图
乙队运动员的成绩统计表
成绩/分 6 7 8 9 10
人数 1 3 5 3
(1) 将下表补充完整.
平均数 众数 中位数
甲队 ____________ 8 ____________
乙队 8.3 ________ 8
(2) 经计算,训练后甲队成绩的方差为,乙队成绩的方差为1.11.综合考虑,王老师很有可能选择哪个队代表学校参加市里比赛?并说明理由.
变式跟进
8.某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数.数据如下:
20 21 19 16 27 18 31 29 21 22
25 20 19 22 35 33 19 17 18 29
18 35 22 15 18 18 31 31 19 22
整理上面的数据,得到如下条形统计图.
样本数据的平均数、众数、中位数如下表所示:
统计量 平均数 众数 中位数
数值 23 21
根据以上信息,解答下列问题:
(1) 上表中众数的值为__________;
(2) 为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获得奖励,应根据________来确定奖励标准比较合适(填“平均数”“众数”或“中位数”);
(3) 该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
过关训练 现复活用
A组·基础达标 逐点击破
1.小明调查了某地1月份一周的最低气温(单位: ),分别是,0,3,,1,0,2,其中以上(不含)出现的频数是( )
A.2 B.3 C.4 D.5
2.[2022自贡]六名同学的年龄(岁)分别是:13,14,15,14,14,15.关于这组数据,正确的说法是( )
A.平均数是14 B.中位数是14.5
C.方差是3 D.众数是14
3.某校四个绿化小组一天植树的棵数分别为9,9,,7,已知这组数据的众数和平均数相等,那么这组数据的中位数是( )
A.8 B.9 C.10 D.12
4.若一组数据,, ,的平均数为5,方差为9,则数据,, ,的平均数为____________,方差为__________.
5.某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科技能力,开展了“最强大脑”邀请赛.现从七、八年级中各随机抽取了20名学生的初赛成绩(初赛成绩均为整数,满分为10分,9分及以上为优秀)统计、整理如下:
七年级抽取的学生的初赛成绩:
6,6,7,7,7,8,8,8,8,8,9,9,9,9,9,9,9,10,10,10.
七、八年级抽取的学生的初赛成绩统计表
年级 平均数 中位数 众数 方差 优秀率
七年级 8.3 8.5 1.41
八年级 8.3 8 7 1.61
根据以上信息,解答下列问题:
(1) 填空:________,__________.
(2) 若该校八年级有900名学生参加初赛,规定满分才可进入复赛,估计八年级进入复赛的学生有____________名.
(3) 根据以上数据,你认为七、八年级学生在“最强大脑”邀请赛中,哪个年级的学生初赛成绩更好?请说明理由(写出一条理由即可).
B组·能力提升 强化突破
6.[2024六安模拟]甲,乙两个小区各有300户居民,为了解这两个小区3月份用户使用燃气量情况,小明和小丽分别从中随机抽取30户进行调查,并对数据进行整理、描述和分析.下面给出了部分信息.
.甲小区用气量频数分布表如下:
分组
频数 3 6 10 3
.乙小区用气量频数直方图如下(数据分成5组:,,,,):
.乙小区用气量的数据在这一组的是:15,15,16,16,16,17,17,18,18,18,18,19
.甲,乙两小区用气量的平均数、中位数、众数如下表:
小区 平均数 中位数 众数
甲 17.4 18 13
乙 17.1 18
根据以上信息,解答下列问题:
(1) 填空:________,____________;
(2) 在甲小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.在乙小区抽取的用户中,记3月份用气量高于他们的平均用气量的户数为.比较,的大小,并说明理由;
(3) 估计甲、乙两小区中用气量不小于的总户数为____________户.
专题5 数据的初步分析
题型归类 举一反三
题型一 频数与频率
例1 D
变式跟进
1.
2.(1)
(2) 解:C组频数为,补全频数直方图略.
(3)
题型二 平均数、中位数、众数
例2 B
【点悟】 找中位数要把数据按大小顺序排列,位于最中间的一个数(数据总数为奇数)或两个数的平均数(数据总数为偶数)为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数为所有数据的和除以数据的个数.
变式跟进
3.(1) 解:甲的平均分为(分),
乙的平均分为(分).
,
乙的综合成绩比甲的高,
应该让乙参加比赛.
(2) 甲的综合成绩为(分),
乙的综合成绩为(分).
, 应该让甲参加比赛.
4.(1) ; ;
(2) 解:八(1)班的复赛成绩较好,理由如下:
两个班级成绩的平均数相同,八(1)班的中位数高,
在平均数相同的情况下,中位数高的八(1)班的复赛成绩较好(答案不唯一).
题型三 方差
例3 (1) 9; 9; 9
(2) 解:;
.
(3) (答案不唯一,合理即可)我认为推荐甲参加省比赛更合适.理由如下:
两人的平均成绩相等,说明实力相当,但甲的六次测试成绩的方差比乙小,说明甲的发挥较为稳定,故推荐甲参加省比赛更合适.
例3 【点悟】 计算方差:“先平均、再作差、平方后、再平均”,也就是说,先求出一组数据的平均数,再将每一个数据都与平均数作差,然后将这些差进行平方,最后求这些差的平方的平均数,其结果就是这组数据的方差.
变式跟进
5.D 6.D
题型四 用样本估计总体
例4 (1) ;
(2)
(3) 解:估计该校1 500名学生中成绩达到95分及以上的学生有(名).
例4 【点悟】 用样本估计总体是统计的核心思想.具体的有用样本平均数估计总体平均数、用样本百分率估计总体百分率、用样本方差估计总体方差等.
变式跟进
7.(1) ; ; ;
(2) 解:八(1)班的众数为10,大于八(2)班的众数,因此八(1)班成绩达到满分的人数较多,满分率较高;八(2)班的方差小于八(1)班的方差,因此八(2)班的成绩比较稳定.
(3)
题型五 分析数据进行决策
例5 (1) ; ;
(2) 解:王老师很有可能会选择甲队作为学校代表参加市里比赛.理由如下:
甲、乙两队的方差相差不大,说明两队成绩整齐程度不相上下,但甲队的平均成绩较高,且甲队10分有4人,9分有6人,均比乙队多,
王老师很有可能会选择甲队作为学校代表参加市里比赛.
例5 【点悟】 分析数据进行决策时,关键在于确定决策侧重的方面,从而可以从平均数、中位数、众数、方差等不同角度出发,衡量各种选择的优劣.
变式跟进
8.(1)
(2) 中位数
(3) 解:(名).
答:估计该部门生产能手的人数为100.
过关训练 现复活用
A组·基础达标 逐点击破
1.B 2.D 3.B
4.;
5.(1) ;
(2)
(3) 解:(答案不唯一,合理即可)根据题意可知,七、八年级的优秀率分别是,,
故七年级的学生初赛成绩更好.
B组·能力提升 强化突破
6.(1) ;
(2) 解:,理由如下:
甲小区的中位数高于平均数,则至少为15户;乙小区高于平均数的户数(户),
.
(3)
