第19章 四边形 质量评估(含答案) 2024-2025学年初中数学沪科版八年级下册
文档属性
| 名称 | 第19章 四边形 质量评估(含答案) 2024-2025学年初中数学沪科版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 222.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 22:44:45 | ||
图片预览


文档简介
第19章 四边形 质量评估
[时量:120分钟 分值:150分]
一、选择题(本大题共10个小题,每小题4分,共40分)
1.若一个边形的内角和为 ,则的值为( )
A.3 B.4 C.5 D.6
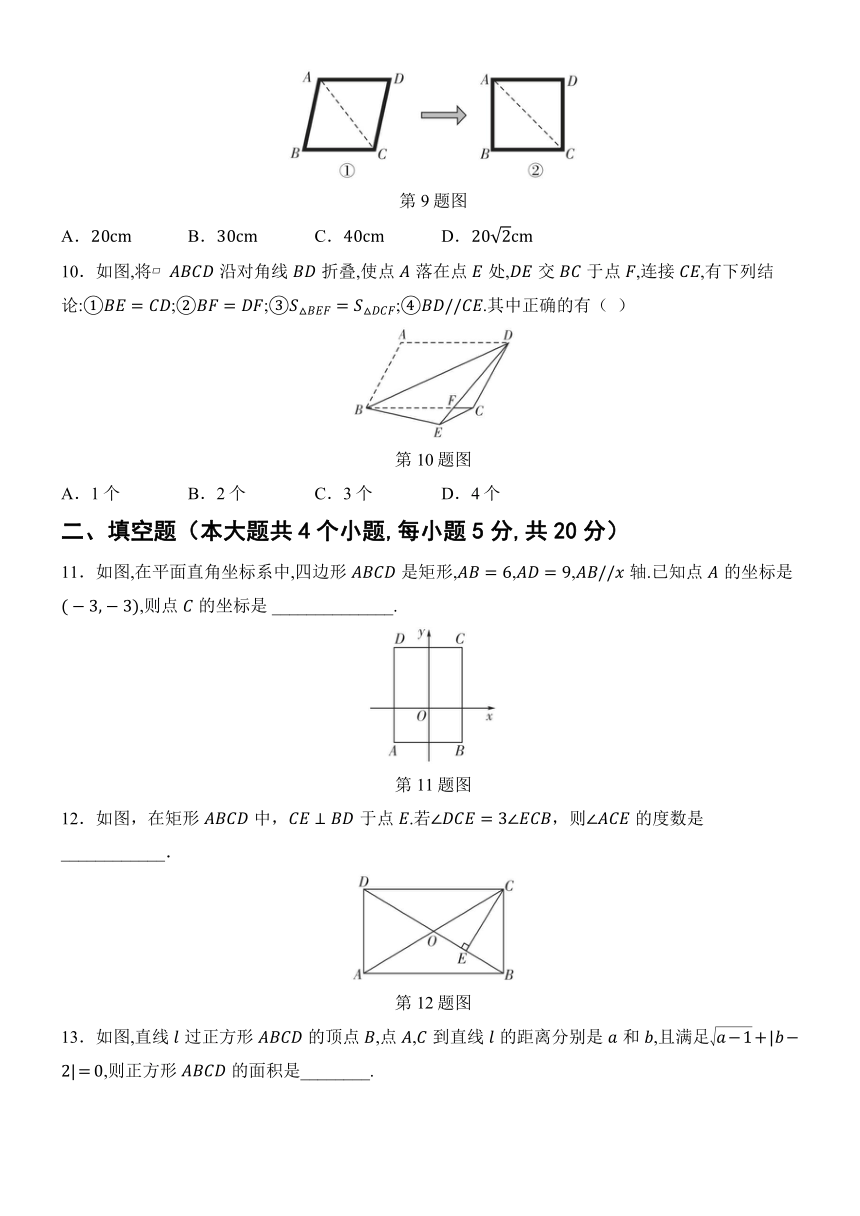
2.直线与正六边形的边,分别相交于点,,如图所示,则 的度数为( )
第2题图
A. B. C. D.
3.如图,四边形是菱形,,,于点,则的长是( )
第3题图
A. B.6 C. D.12
4.如图,在中,对角线,相交于点,,是对角线上的两点,当点,满足下列条件时,四边形不一定是平行四边形的是( )
第4题图
A. B.
C. D.
5.如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形的边长是,则图中阴影图形的周长是( )
第5题图
A. B. C. D.
6.如图,四边形为矩形,过点,作对角线的垂线,垂足为分别为,,过点,作对角线的垂线,垂足分别为,.如果四条垂线拼成一个四边形,那么这个四边形为( )
A.菱形 B.矩形 C.直角梯形 D.等腰梯形
7.如图,的对角线,相交于点,,.若,,则四边形的周长为( )
第7题图
A.4 B.6 C.8 D.16
8.如图,在中,对角线与交于点,,为的中点.若,则的长为( )
第8题图
A. B.9 C. D.10
9.小明用四根长度相等的木条制作了能够活动的菱形学具,他先活动学具成为图①所示的菱形,并测得 ,接着活动学具成为图②所示的正方形,并测得对角线,则图①中对角线的长为( )
第9题图
A. B. C. D.
10.如图,将沿对角线折叠,使点落在点处,交于点,连接,有下列结论:;;;.其中正确的有( )
第10题图
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4个小题,每小题5分,共20分)
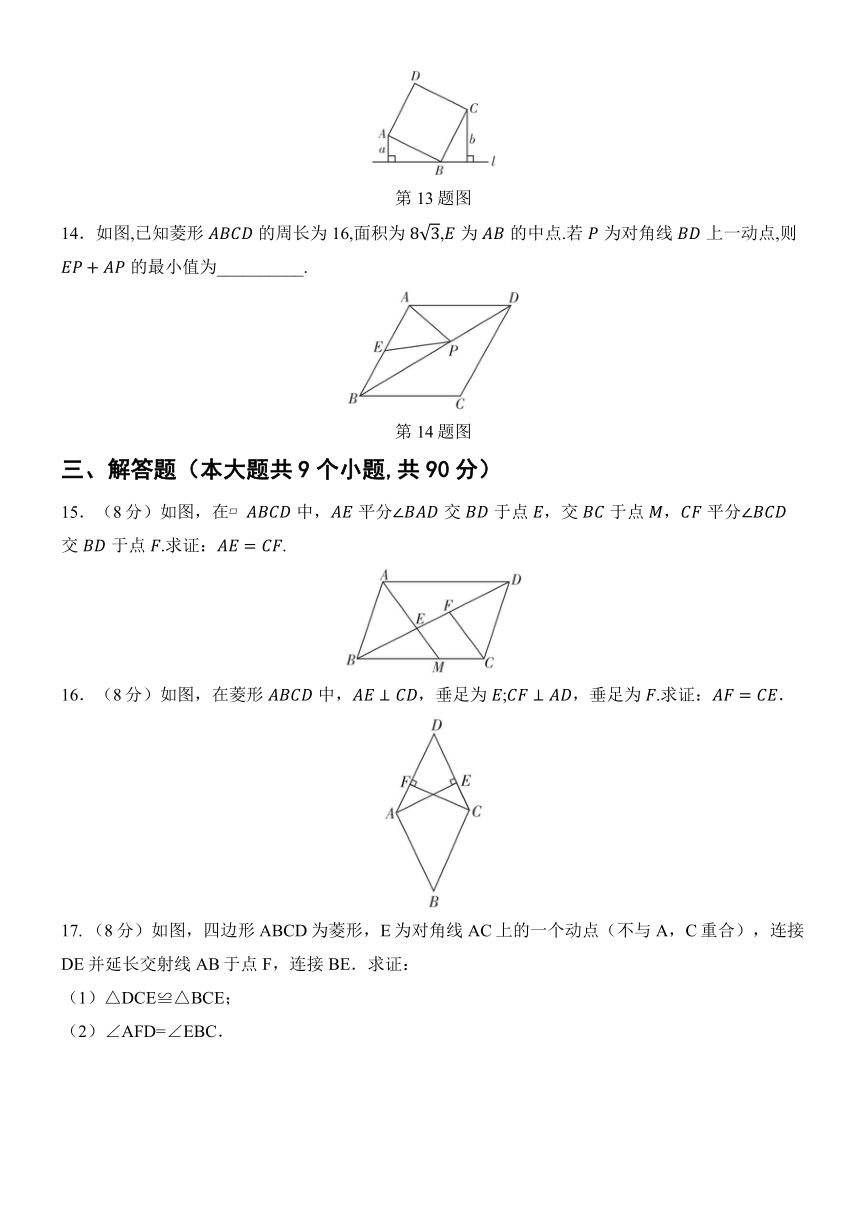
11.如图,在平面直角坐标系中,四边形是矩形,,,轴.已知点的坐标是,则点的坐标是 ______________.
第11题图
12.如图,在矩形中,于点.若,则的度数是____________.
第12题图
13.如图,直线过正方形的顶点,点,到直线的距离分别是和,且满足,则正方形的面积是________.
第13题图
14.如图,已知菱形的周长为16,面积为,为的中点.若为对角线上一动点,则的最小值为__________.
第14题图
三、解答题(本大题共9个小题,共90分)
15.(8分)如图,在中,平分交于点,交于点,平分交于点.求证:.
16.(8分)如图,在菱形中,,垂足为;,垂足为.求证:.
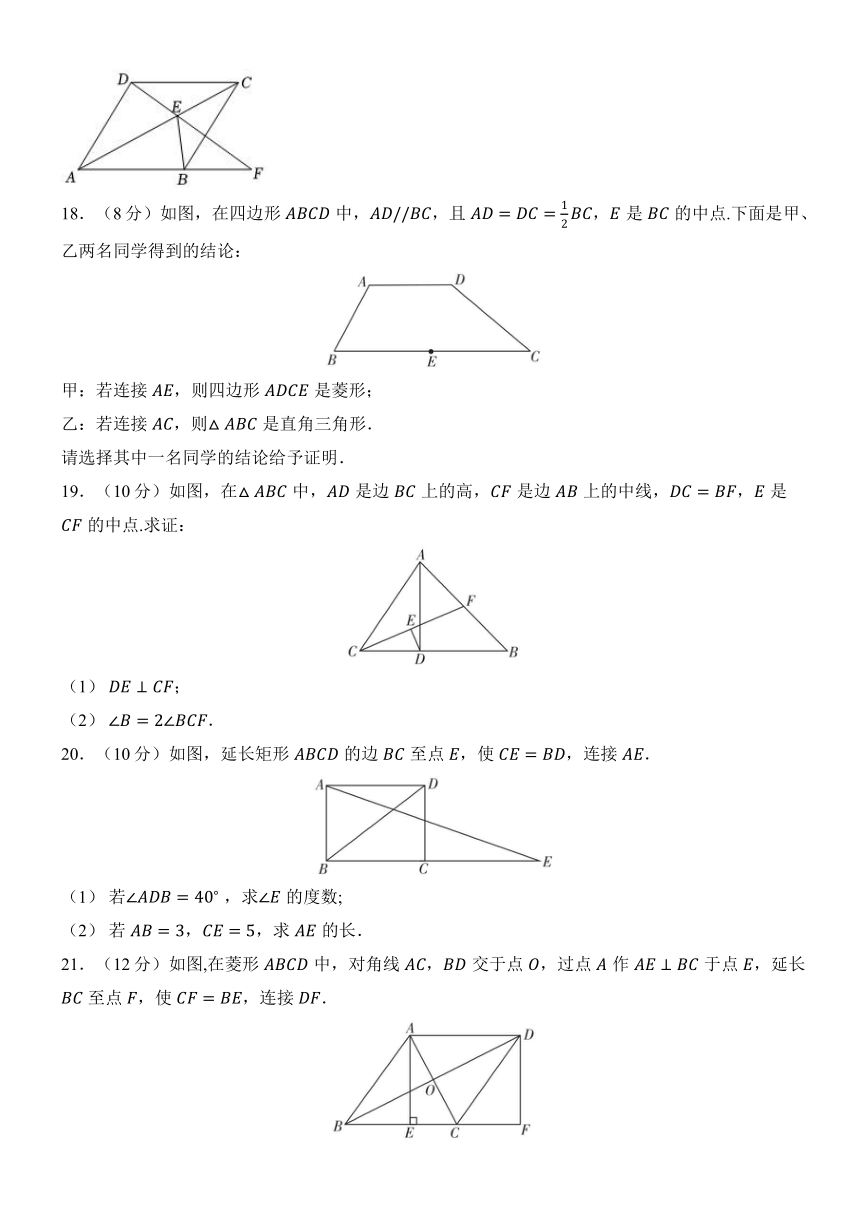
17. (8分)如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与A,C重合),连接DE并延长交射线AB于点F,连接BE.求证:
(1)△DCE≌△BCE;
(2)∠AFD=∠EBC.
18.(8分)如图,在四边形中,,且,是的中点.下面是甲、乙两名同学得到的结论:
甲:若连接,则四边形是菱形;
乙:若连接,则是直角三角形.
请选择其中一名同学的结论给予证明.
19.(10分)如图,在中,是边上的高,是边上的中线,,是的中点.求证:
(1) ;
(2) .
20.(10分)如图,延长矩形的边至点,使,连接.
(1) 若 ,求的度数;
(2) 若,,求的长.
21.(12分)如图,在菱形中,对角线,交于点,过点作于点,延长至点,使,连接.
(1) 求证:四边形是矩形;
(2) 若,,求的长.
22.(12分)【方法回顾】
(1) 如图①,过正方形的顶点作一条直线交边于点,于点,于点,求证:;
【问题解决】
(2) 如图②,菱形的边长为,过点作一条直线交边于点,且 ,是上一点,且 ,过点作,与直线交于点,若,求的长.
23.(14分)几何与探究
【初步感知】
(1) 如图①,在中, ,,将沿折叠,使点与点重合,折痕与交于点,已知,求的长;
【深入探究】
(2) 如图②,将矩形沿着对角线折叠,使点落在处,交于点,若,,求的长;
【拓展延伸】
(3) 如图③,在矩形中,,,点在边上,点在边上,将纸片沿折叠,使顶点落在点处.若,连接.当时,求的长.
第19章质量评估
一、选择题(本大题共10个小题,每小题4分,共40分)
1.C 2.B 3.A 4.A 5.A 6.A 7.C 8.C 9.D 10.D
二、填空题(本大题共4个小题,每小题5分,共20分)
11.
12.
13.
14.
三、解答题(本大题共9个小题,共90分)
15.证明: 四边形是平行四边形,
,,,
.
平分,平分,
,,
.
在和中,
,
.
16.证明: 四边形是菱形,.
,
.
在和中,
,
,,.
证明:(1)∵四边形ABCD是菱形,
∴CD=CB,∠ACD=∠ACB,
在△DCE和△BCE中,
∴△DCE≌△BCE(SAS).
(2)∵△DCE≌△BCE,
∴∠CDE=∠CBE,
∵CD∥AB,
∴∠CDE=∠AFD,
∴∠EBC=∠AFD,即∠AFD=∠EBC.
18.证明:选择甲:如答图①.
第21题答图①
是的中点,.
,.
, 四边形是平行四边形.
, 四边形是菱形.
选择乙:连接,,交于于点,如答图②.
第21题答图②
,是的中点,
.
,
四边形,四边形都是平行四边形,.
,
是菱形,, .,
,
是直角三角形.
19.(1) 证明:连接,如答图.
第22题答图
是边上的高, .
是的中点,.
,,
是的中点..
(2) ,,
.
,,
.
20.(1) 解:连接交于点,如答图.
第23题答图
四边形是矩形,,
,,
.
, .
,
.
(2) ,,
.
.
.
21.(1) 证明:在菱形中,,.
,,,.
, 四边形是平行四边形.
,即 , 四边形是矩形.
(2) 解:在菱形中,.
,.
在矩形中, ,,
在中, ,
解得,即的长为10.
22.(1) 证明: 四边形是正方形,
, , .
,
..
又,
.
,,.
,.
(2) 解: 四边形是菱形,.
, .
,即 .
,,
,
,
,,
,解得,
的长为.
23.(1) 解:,,.
由折叠可知:.
,,.
(2) 由折叠可知:.
四边形为矩形,, ,
,,.
设,则.
,即,解得,
的长为.
(3) 过点作于点,如答图,
.
,
,.
.
又,,
.
,,,
,,解得,
的长为.
第26题答图
[时量:120分钟 分值:150分]
一、选择题(本大题共10个小题,每小题4分,共40分)
1.若一个边形的内角和为 ,则的值为( )
A.3 B.4 C.5 D.6
2.直线与正六边形的边,分别相交于点,,如图所示,则 的度数为( )
第2题图
A. B. C. D.
3.如图,四边形是菱形,,,于点,则的长是( )
第3题图
A. B.6 C. D.12
4.如图,在中,对角线,相交于点,,是对角线上的两点,当点,满足下列条件时,四边形不一定是平行四边形的是( )
第4题图
A. B.
C. D.
5.如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形的边长是,则图中阴影图形的周长是( )
第5题图
A. B. C. D.
6.如图,四边形为矩形,过点,作对角线的垂线,垂足为分别为,,过点,作对角线的垂线,垂足分别为,.如果四条垂线拼成一个四边形,那么这个四边形为( )
A.菱形 B.矩形 C.直角梯形 D.等腰梯形
7.如图,的对角线,相交于点,,.若,,则四边形的周长为( )
第7题图
A.4 B.6 C.8 D.16
8.如图,在中,对角线与交于点,,为的中点.若,则的长为( )
第8题图
A. B.9 C. D.10
9.小明用四根长度相等的木条制作了能够活动的菱形学具,他先活动学具成为图①所示的菱形,并测得 ,接着活动学具成为图②所示的正方形,并测得对角线,则图①中对角线的长为( )
第9题图
A. B. C. D.
10.如图,将沿对角线折叠,使点落在点处,交于点,连接,有下列结论:;;;.其中正确的有( )
第10题图
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共4个小题,每小题5分,共20分)
11.如图,在平面直角坐标系中,四边形是矩形,,,轴.已知点的坐标是,则点的坐标是 ______________.
第11题图
12.如图,在矩形中,于点.若,则的度数是____________.
第12题图
13.如图,直线过正方形的顶点,点,到直线的距离分别是和,且满足,则正方形的面积是________.
第13题图
14.如图,已知菱形的周长为16,面积为,为的中点.若为对角线上一动点,则的最小值为__________.
第14题图
三、解答题(本大题共9个小题,共90分)
15.(8分)如图,在中,平分交于点,交于点,平分交于点.求证:.
16.(8分)如图,在菱形中,,垂足为;,垂足为.求证:.
17. (8分)如图,四边形ABCD为菱形,E为对角线AC上的一个动点(不与A,C重合),连接DE并延长交射线AB于点F,连接BE.求证:
(1)△DCE≌△BCE;
(2)∠AFD=∠EBC.
18.(8分)如图,在四边形中,,且,是的中点.下面是甲、乙两名同学得到的结论:
甲:若连接,则四边形是菱形;
乙:若连接,则是直角三角形.
请选择其中一名同学的结论给予证明.
19.(10分)如图,在中,是边上的高,是边上的中线,,是的中点.求证:
(1) ;
(2) .
20.(10分)如图,延长矩形的边至点,使,连接.
(1) 若 ,求的度数;
(2) 若,,求的长.
21.(12分)如图,在菱形中,对角线,交于点,过点作于点,延长至点,使,连接.
(1) 求证:四边形是矩形;
(2) 若,,求的长.
22.(12分)【方法回顾】
(1) 如图①,过正方形的顶点作一条直线交边于点,于点,于点,求证:;
【问题解决】
(2) 如图②,菱形的边长为,过点作一条直线交边于点,且 ,是上一点,且 ,过点作,与直线交于点,若,求的长.
23.(14分)几何与探究
【初步感知】
(1) 如图①,在中, ,,将沿折叠,使点与点重合,折痕与交于点,已知,求的长;
【深入探究】
(2) 如图②,将矩形沿着对角线折叠,使点落在处,交于点,若,,求的长;
【拓展延伸】
(3) 如图③,在矩形中,,,点在边上,点在边上,将纸片沿折叠,使顶点落在点处.若,连接.当时,求的长.
第19章质量评估
一、选择题(本大题共10个小题,每小题4分,共40分)
1.C 2.B 3.A 4.A 5.A 6.A 7.C 8.C 9.D 10.D
二、填空题(本大题共4个小题,每小题5分,共20分)
11.
12.
13.
14.
三、解答题(本大题共9个小题,共90分)
15.证明: 四边形是平行四边形,
,,,
.
平分,平分,
,,
.
在和中,
,
.
16.证明: 四边形是菱形,.
,
.
在和中,
,
,,.
证明:(1)∵四边形ABCD是菱形,
∴CD=CB,∠ACD=∠ACB,
在△DCE和△BCE中,
∴△DCE≌△BCE(SAS).
(2)∵△DCE≌△BCE,
∴∠CDE=∠CBE,
∵CD∥AB,
∴∠CDE=∠AFD,
∴∠EBC=∠AFD,即∠AFD=∠EBC.
18.证明:选择甲:如答图①.
第21题答图①
是的中点,.
,.
, 四边形是平行四边形.
, 四边形是菱形.
选择乙:连接,,交于于点,如答图②.
第21题答图②
,是的中点,
.
,
四边形,四边形都是平行四边形,.
,
是菱形,, .,
,
是直角三角形.
19.(1) 证明:连接,如答图.
第22题答图
是边上的高, .
是的中点,.
,,
是的中点..
(2) ,,
.
,,
.
20.(1) 解:连接交于点,如答图.
第23题答图
四边形是矩形,,
,,
.
, .
,
.
(2) ,,
.
.
.
21.(1) 证明:在菱形中,,.
,,,.
, 四边形是平行四边形.
,即 , 四边形是矩形.
(2) 解:在菱形中,.
,.
在矩形中, ,,
在中, ,
解得,即的长为10.
22.(1) 证明: 四边形是正方形,
, , .
,
..
又,
.
,,.
,.
(2) 解: 四边形是菱形,.
, .
,即 .
,,
,
,
,,
,解得,
的长为.
23.(1) 解:,,.
由折叠可知:.
,,.
(2) 由折叠可知:.
四边形为矩形,, ,
,,.
设,则.
,即,解得,
的长为.
(3) 过点作于点,如答图,
.
,
,.
.
又,,
.
,,,
,,解得,
的长为.
第26题答图
