滚动周练(三)第18章 勾股定理 2024-2025学年初中数学沪科版八年级下册单元专题练(含答案)
文档属性
| 名称 | 滚动周练(三)第18章 勾股定理 2024-2025学年初中数学沪科版八年级下册单元专题练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 150.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 07:54:02 | ||
图片预览

文档简介
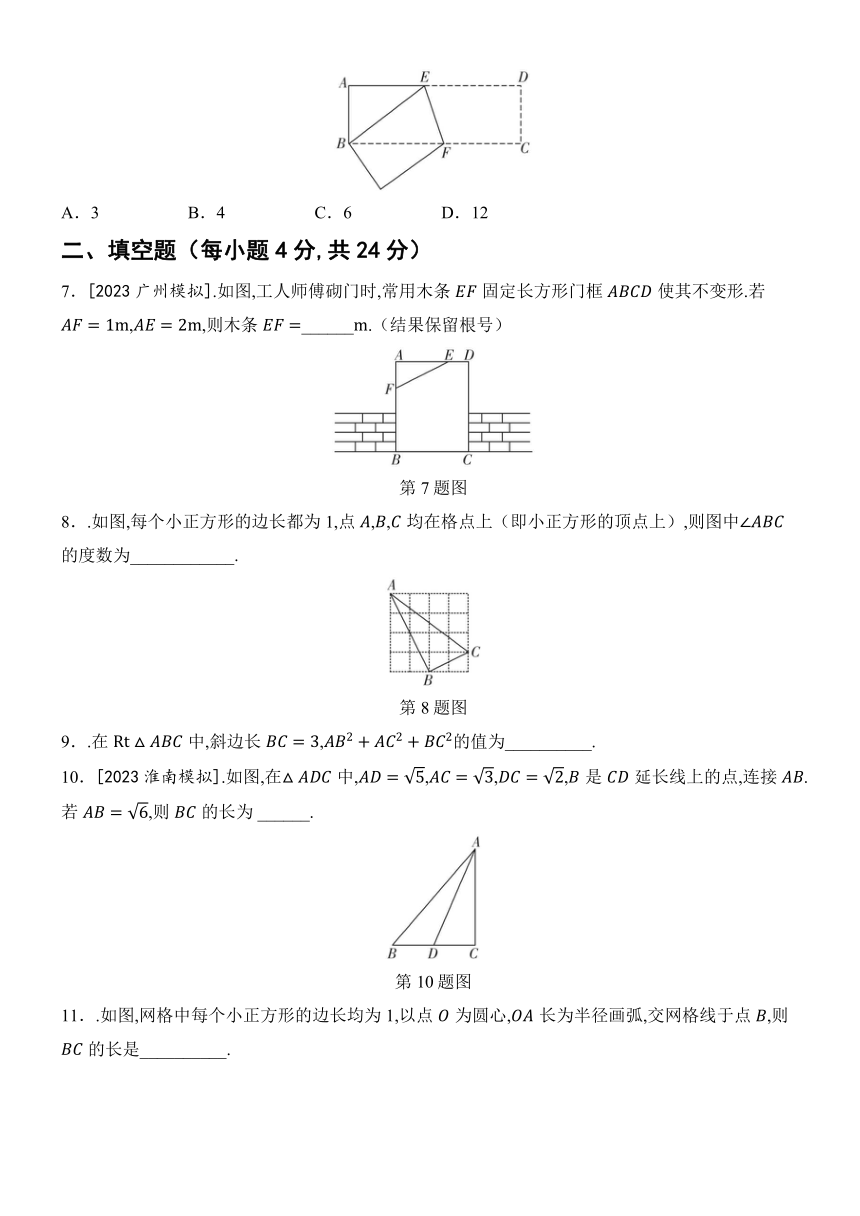
滚动周练(三)第18章 勾股定理
一、选择题(每小题5分,共30分)
1..下列四组数据是勾股数的是( )
A.2,3,4 B.,, C.8,11,12 D.6,8,10
2.[2023滁州模拟].在中, ,,,则边的长为( )
A.1 B. C. D.2
3.[2023合肥模拟].如图,在中, ,若,,则正方形的面积为( )
第3题图
A.4 B. C.13 D.16
4..若,,是的三边长,且,,,则最长边上的高是( )
A. B. C. D.
5.[2023合肥模拟].如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,则小巷的宽为( )
第5题图
A. B. C. D.
6..如图,在长方形中,,,将此长方形折叠,使点与点重合,折痕为,则的面积为( )
A.3 B.4 C.6 D.12
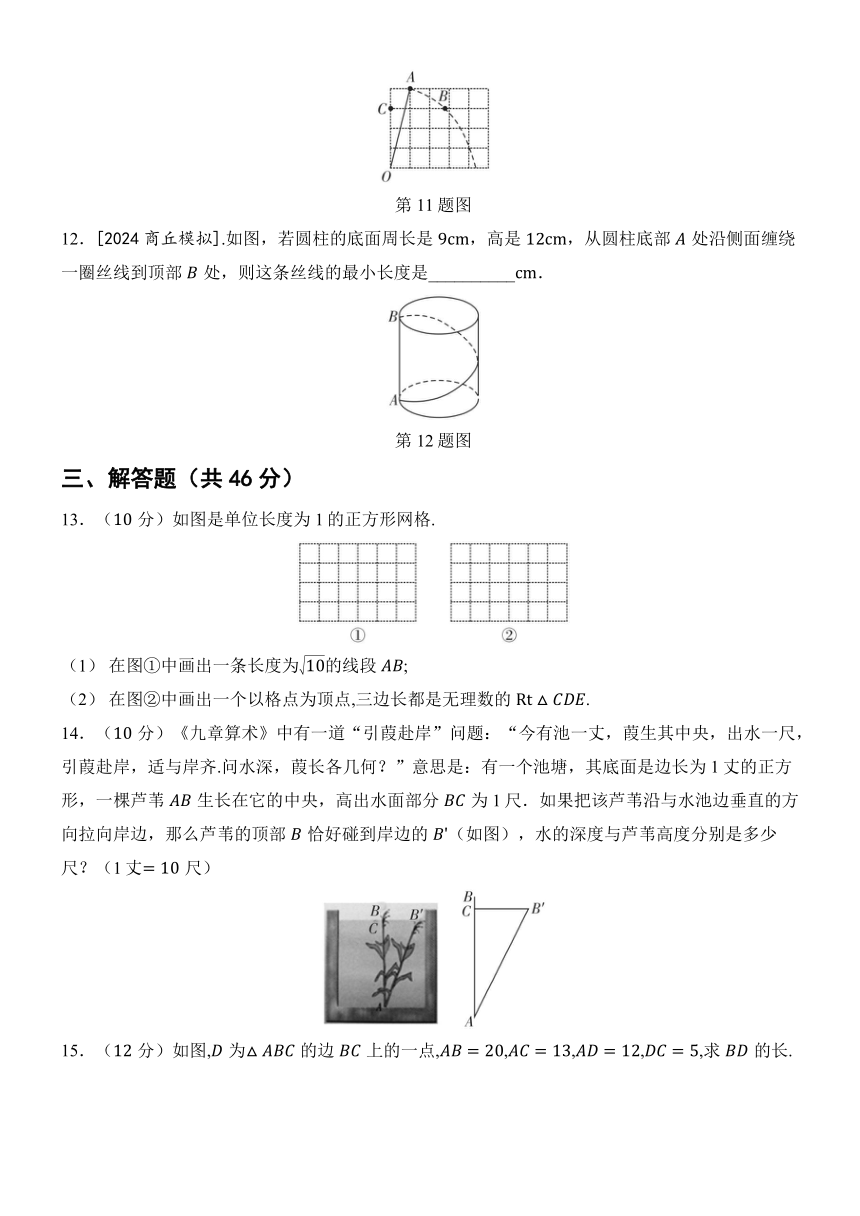
二、填空题(每小题4分,共24分)
7.[2023广州模拟].如图,工人师傅砌门时,常用木条固定长方形门框使其不变形.若,,则木条______.(结果保留根号)
第7题图
8..如图,每个小正方形的边长都为1,点,,均在格点上(即小正方形的顶点上),则图中的度数为____________.
第8题图
9..在中,斜边长,的值为__________.
10.[2023淮南模拟].如图,在中,,,,是延长线上的点,连接.若,则的长为 ______.
第10题图
11..如图,网格中每个小正方形的边长均为1,以点为圆心,长为半径画弧,交网格线于点,则的长是__________.
第11题图
12.[2024商丘模拟].如图,若圆柱的底面周长是,高是,从圆柱底部处沿侧面缠绕一圈丝线到顶部处,则这条丝线的最小长度是__________.
第12题图
三、解答题(共46分)
13.(分)如图是单位长度为1的正方形网格.
(1) 在图①中画出一条长度为的线段;
(2) 在图②中画出一个以格点为顶点,三边长都是无理数的.
14.(分)《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”意思是:有一个池塘,其底面是边长为1丈的正方形,一棵芦苇生长在它的中央,高出水面部分为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边的(如图),水的深度与芦苇高度分别是多少尺?(1丈尺)
15.(分)如图,为的边上的一点,,,,,求的长.
16.(分)“数形结合”和“建模思想”是数学中的两个很重要的思想方法,阅读以下材料:
例:求代数式 的最小值.
分析:和 是勾股定理的形式,是直角边分别是 和3的直角三角形的斜边长,是直角边分别是 和2的直角三角形的斜边长,因此,我们构造两个直角 和,并使直角边 和 在同一直线上(图①),向右平移直角 使点 和 重合(图②),这时有,,,问题就变成“点 在线段 的何处时,最短?”根据两点间线段最短,得到线段 就是它们的最小值.
解答下面问题:
(1) 代数式的最小值为__________;
(2) 代数式的最小值为____________;
(3) 解方程(利用几何方法解答).
,
滚动周练(三)
一、选择题(每小题5分,共30分)
1.D 2.B 3.C 4.C 5.D 6.C
二、填空题(每小题4分,共24分)
7.
8.
9.
10.
11.
12.
三、解答题(共46分)
13.(1) 解:如答图①,根据勾股定理,得,故即为所求作.
第13题答图①
(2) 如答图②,根据勾股定理,得,,,
故即为所求作.(答案不唯一)
第13题答图②
14.解:设水深尺,则芦苇长尺.
根据题意,得,
解得.
.
答:水深12尺,芦苇长13尺.
15.解:,,,且,
,
是直角三角形, ,
.
,,
.
16.(1)
(2)
(3) 解:如答图,构造, ,于点,且,.
第16题答图
设,
在中,.
在中,.
在中,.
,即.
线段的长为方程的一个实数解.
.
另外,也是方程的实数解,
方程的解为.
一、选择题(每小题5分,共30分)
1..下列四组数据是勾股数的是( )
A.2,3,4 B.,, C.8,11,12 D.6,8,10
2.[2023滁州模拟].在中, ,,,则边的长为( )
A.1 B. C. D.2
3.[2023合肥模拟].如图,在中, ,若,,则正方形的面积为( )
第3题图
A.4 B. C.13 D.16
4..若,,是的三边长,且,,,则最长边上的高是( )
A. B. C. D.
5.[2023合肥模拟].如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为,梯子顶端到地面的距离为.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为,则小巷的宽为( )
第5题图
A. B. C. D.
6..如图,在长方形中,,,将此长方形折叠,使点与点重合,折痕为,则的面积为( )
A.3 B.4 C.6 D.12
二、填空题(每小题4分,共24分)
7.[2023广州模拟].如图,工人师傅砌门时,常用木条固定长方形门框使其不变形.若,,则木条______.(结果保留根号)
第7题图
8..如图,每个小正方形的边长都为1,点,,均在格点上(即小正方形的顶点上),则图中的度数为____________.
第8题图
9..在中,斜边长,的值为__________.
10.[2023淮南模拟].如图,在中,,,,是延长线上的点,连接.若,则的长为 ______.
第10题图
11..如图,网格中每个小正方形的边长均为1,以点为圆心,长为半径画弧,交网格线于点,则的长是__________.
第11题图
12.[2024商丘模拟].如图,若圆柱的底面周长是,高是,从圆柱底部处沿侧面缠绕一圈丝线到顶部处,则这条丝线的最小长度是__________.
第12题图
三、解答题(共46分)
13.(分)如图是单位长度为1的正方形网格.
(1) 在图①中画出一条长度为的线段;
(2) 在图②中画出一个以格点为顶点,三边长都是无理数的.
14.(分)《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”意思是:有一个池塘,其底面是边长为1丈的正方形,一棵芦苇生长在它的中央,高出水面部分为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部恰好碰到岸边的(如图),水的深度与芦苇高度分别是多少尺?(1丈尺)
15.(分)如图,为的边上的一点,,,,,求的长.
16.(分)“数形结合”和“建模思想”是数学中的两个很重要的思想方法,阅读以下材料:
例:求代数式 的最小值.
分析:和 是勾股定理的形式,是直角边分别是 和3的直角三角形的斜边长,是直角边分别是 和2的直角三角形的斜边长,因此,我们构造两个直角 和,并使直角边 和 在同一直线上(图①),向右平移直角 使点 和 重合(图②),这时有,,,问题就变成“点 在线段 的何处时,最短?”根据两点间线段最短,得到线段 就是它们的最小值.
解答下面问题:
(1) 代数式的最小值为__________;
(2) 代数式的最小值为____________;
(3) 解方程(利用几何方法解答).
,
滚动周练(三)
一、选择题(每小题5分,共30分)
1.D 2.B 3.C 4.C 5.D 6.C
二、填空题(每小题4分,共24分)
7.
8.
9.
10.
11.
12.
三、解答题(共46分)
13.(1) 解:如答图①,根据勾股定理,得,故即为所求作.
第13题答图①
(2) 如答图②,根据勾股定理,得,,,
故即为所求作.(答案不唯一)
第13题答图②
14.解:设水深尺,则芦苇长尺.
根据题意,得,
解得.
.
答:水深12尺,芦苇长13尺.
15.解:,,,且,
,
是直角三角形, ,
.
,,
.
16.(1)
(2)
(3) 解:如答图,构造, ,于点,且,.
第16题答图
设,
在中,.
在中,.
在中,.
,即.
线段的长为方程的一个实数解.
.
另外,也是方程的实数解,
方程的解为.
