期末质量评估(含答案)2024-2025学年初中数学沪科版八年级下册
文档属性
| 名称 | 期末质量评估(含答案)2024-2025学年初中数学沪科版八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 183.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 07:55:30 | ||
图片预览

文档简介
期末质量评估
[时量:120分钟 分值:150分]
一、选择题(本大题共12个小题,每小题3分,共36分)
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.如图,小张想估测被池塘隔开的,两处景观之间的距离,他先在外取一点,然后步测出,的中点,,并步测出的长约为,由此估测,之间的距离为( )
第2题图
A. B. C. D.
3.下列说法错误的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相平分的四边形是平行四边形
4.已知,则的值为( )
A. B. C.2 024 D.2 025
5.某品牌女运动鞋专卖店,老板统计了一周内不同鞋码运动鞋的销售量如表:
鞋码 36 37 38 39 40
平均每天销售量/双 10 12 20 12 12
如果每双鞋的利润相同,你认为老板最关注的销售数据是下列统计量中的( )
A.平均数 B.中位数 C.众数 D.方差
6.若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B.且
C.且 D.
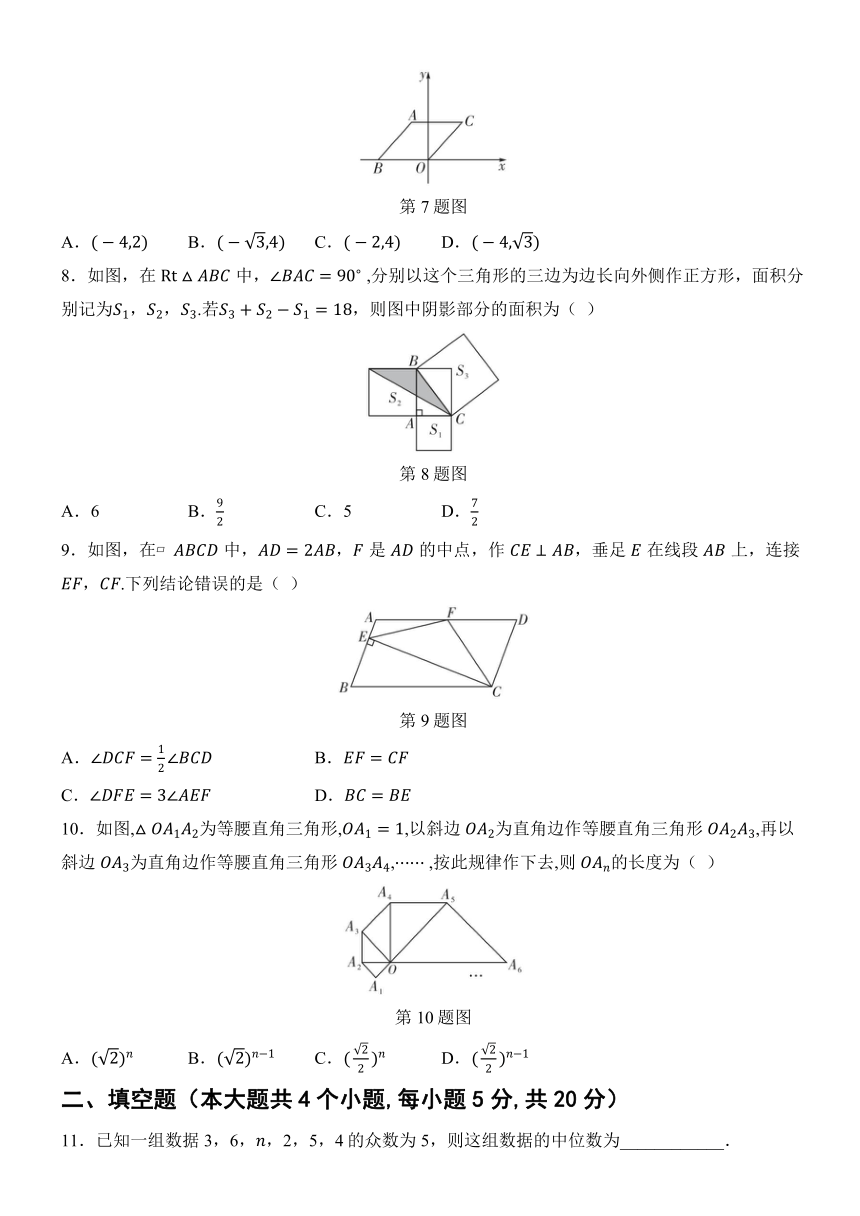
7.如图,是坐标原点,菱形的顶点在轴的负半轴上,顶点的坐标为,则顶点的坐标为( )
第7题图
A. B. C. D.
8.如图,在中, ,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为,,.若,则图中阴影部分的面积为( )
第8题图
A.6 B. C.5 D.
9.如图,在中,,是的中点,作,垂足在线段上,连接,.下列结论错误的是( )
第9题图
A. B.
C. D.
10.如图,为等腰直角三角形,,以斜边为直角边作等腰直角三角形,再以斜边为直角边作等腰直角三角形, ,按此规律作下去,则的长度为( )
第10题图
A. B. C. D.
二、填空题(本大题共4个小题,每小题5分,共20分)
11.已知一组数据3,6,,2,5,4的众数为5,则这组数据的中位数为____________.
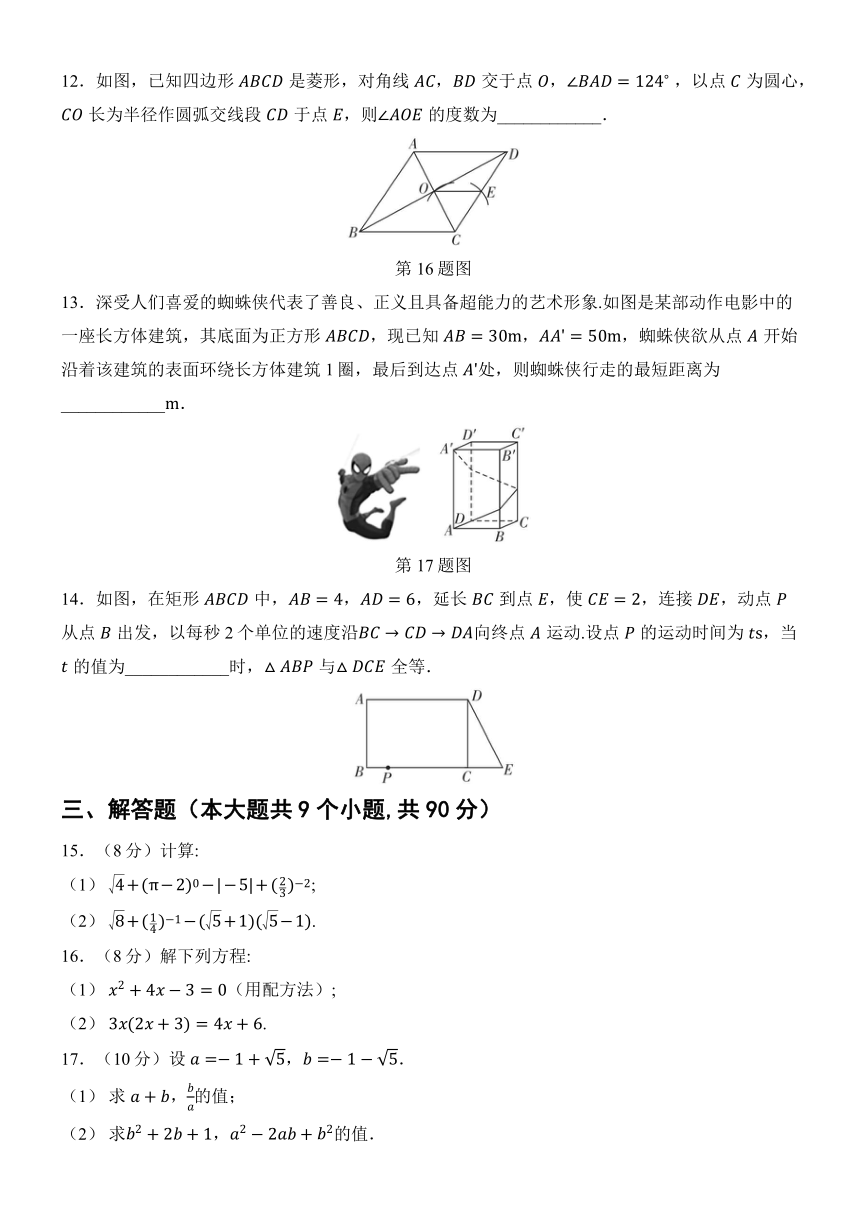
12.如图,已知四边形是菱形,对角线,交于点, ,以点为圆心,长为半径作圆弧交线段于点,则的度数为____________.
第16题图
13.深受人们喜爱的蜘蛛侠代表了善良、正义且具备超能力的艺术形象.如图是某部动作电影中的一座长方体建筑,其底面为正方形,现已知,,蜘蛛侠欲从点开始沿着该建筑的表面环绕长方体建筑1圈,最后到达点处,则蜘蛛侠行走的最短距离为____________.
第17题图
14.如图,在矩形中,,,延长到点,使,连接,动点从点出发,以每秒2个单位的速度沿向终点运动.设点的运动时间为,当的值为____________时,与全等.
三、解答题(本大题共9个小题,共90分)
15.(8分)计算:
(1) ;
(2) .
16.(8分)解下列方程:
(1) (用配方法);
(2) .
17.(10分)设,.
(1) 求,的值;
(2) 求,的值.
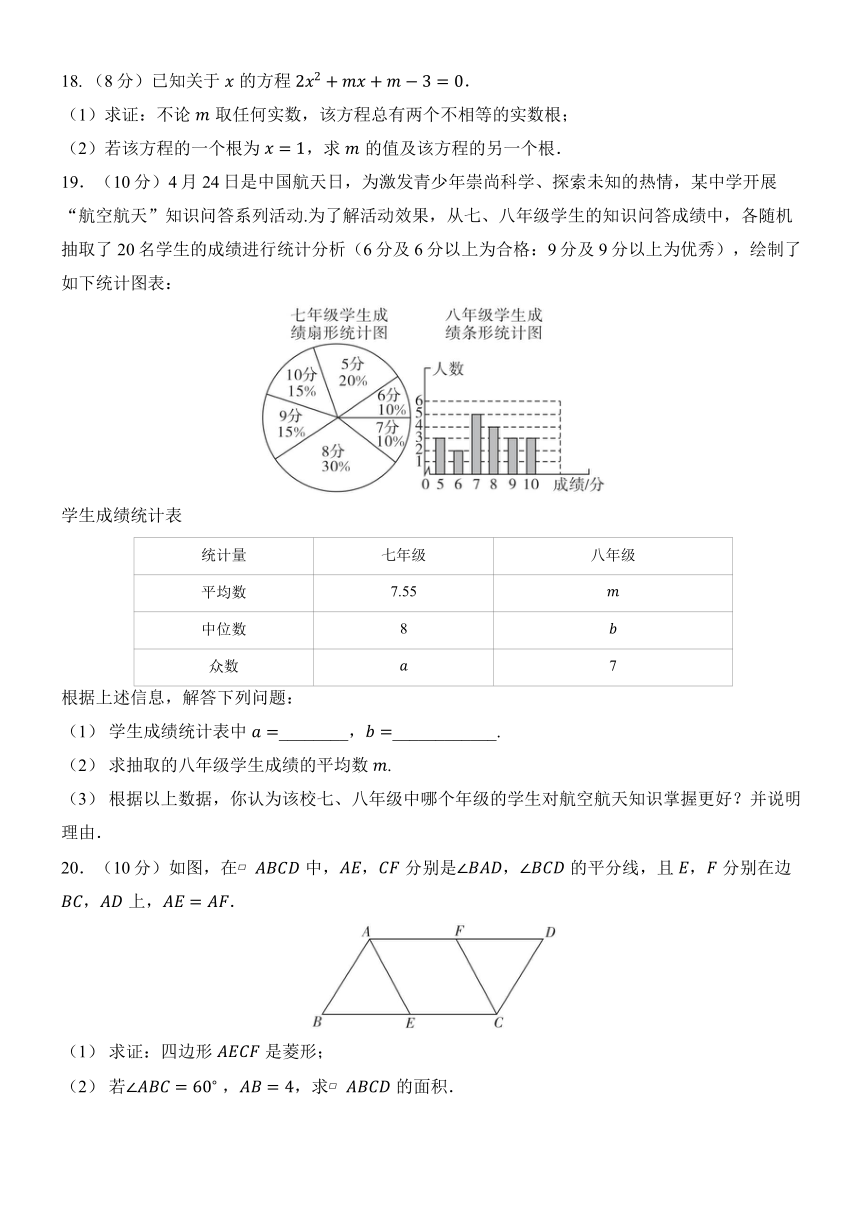
18. (8分)已知关于的方程.
(1)求证:不论取任何实数,该方程总有两个不相等的实数根;
(2)若该方程的一个根为,求的值及该方程的另一个根.
19.(10分)4月24日是中国航天日,为激发青少年崇尚科学、探索未知的热情,某中学开展“航空航天”知识问答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析(6分及6分以上为合格:9分及9分以上为优秀),绘制了如下统计图表:
学生成绩统计表
统计量 七年级 八年级
平均数 7.55
中位数 8
众数 7
根据上述信息,解答下列问题:
(1) 学生成绩统计表中________,____________.
(2) 求抽取的八年级学生成绩的平均数.
(3) 根据以上数据,你认为该校七、八年级中哪个年级的学生对航空航天知识掌握更好?并说明理由.
20.(10分)如图,在中,,分别是,的平分线,且,分别在边,上,.
(1) 求证:四边形是菱形;
(2) 若 ,,求的面积.
21.(12分)如图,在菱形中,对角线,交于点,过点作的垂线,垂足为,延长到点,使,连接.
(1) 求证:四边形是矩形;
(2) 若,,求的长.
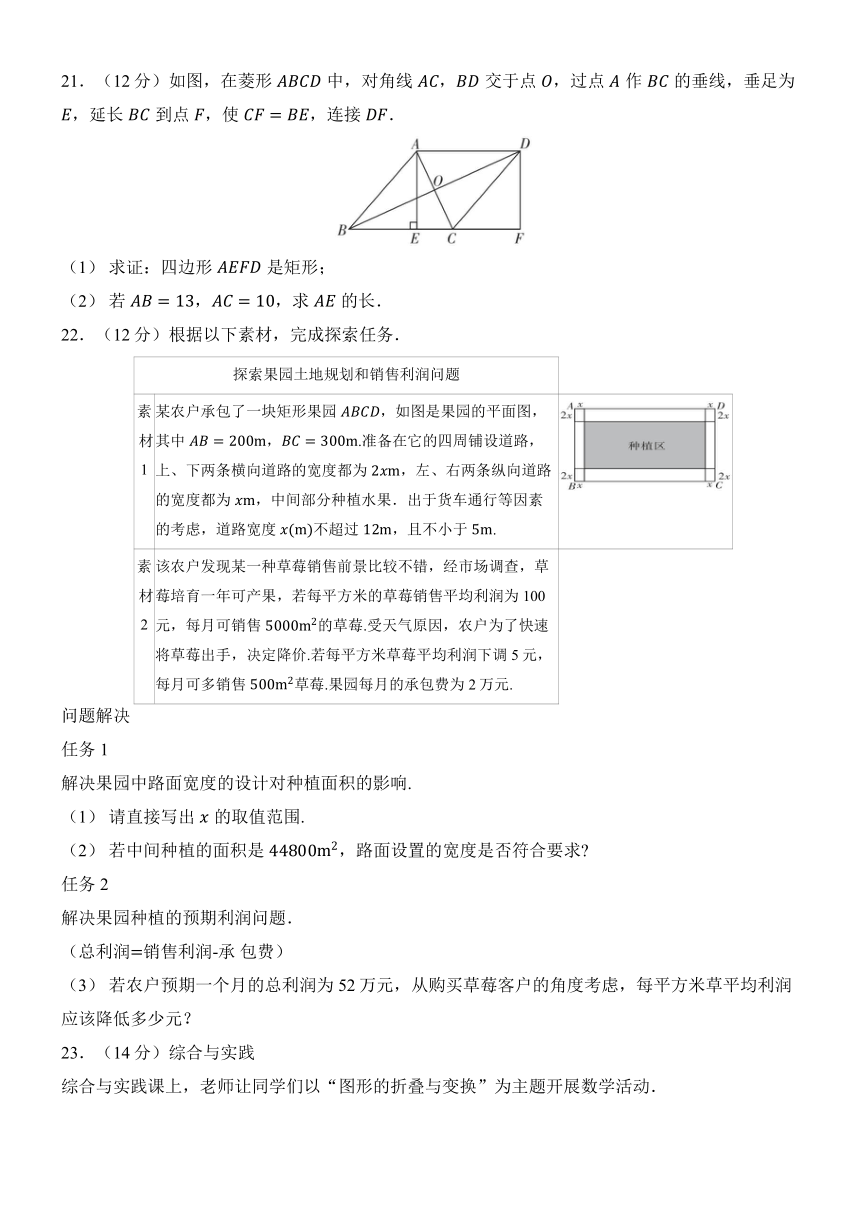
22.(12分)根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材1 某农户承包了一块矩形果园,如图是果园的平面图,其中,.准备在它的四周铺设道路,上、下两条横向道路的宽度都为,左、右两条纵向道路的宽度都为,中间部分种植水果.出于货车通行等因素的考虑,道路宽度不超过,且不小于.
素材2 该农户发现某一种草莓销售前景比较不错,经市场调查,草莓培育一年可产果,若每平方米的草莓销售平均利润为100元,每月可销售的草莓.受天气原因,农户为了快速将草莓出手,决定降价.若每平方米草莓平均利润下调5元,每月可多销售草莓.果园每月的承包费为2万元.
问题解决
任务1
解决果园中路面宽度的设计对种植面积的影响.
(1) 请直接写出的取值范围.
(2) 若中间种植的面积是,路面设置的宽度是否符合要求
任务2
解决果园种植的预期利润问题.
(总利润销售利润-承 包费)
(3) 若农户预期一个月的总利润为52万元,从购买草莓客户的角度考虑,每平方米草平均利润应该降低多少元?
23.(14分)综合与实践
综合与实践课上,老师让同学们以“图形的折叠与变换”为主题开展数学活动.
(1) 【操作判断】
操作一:如图①,将矩形纸片折叠,使落在边上,点与点重合,折痕为.
根据以上操作:四边形的形状是________.
操作二:沿剪开,将四边形折叠,使边,都落在四边形的对角线上,折痕为,,连接,如图②.
根据以上操作:的度数为____________;线段,,的数量关系是__________________.
(2) 【迁移探究】
如图③,在,上分别取点,,使和图②中的度数相等,连接,探究线段,,之间的数量关系,并说明理由.
(3) 【拓展应用】
在(2)的探究下,连接对角线,若图③中的的边,分别交对角线于点,,将纸片沿对角线剪开,如图④,若,,求出的长.
期末质量评估
一、选择题(本大题共10个小题,每小题4分,共40分)
1.B 2.C 3.C 4.B 5.C 6.B 7.C 8.B 9.D 10.B
二、填空题(本大题共4个小题,每小题5分,共20分)
11.
12.
13.
14.或7
三、解答题(本大题共9个小题,共90分)
15.(1) 解:原式.
(2) 原式.
16.(1) 解:整理,得,
配方,得,即,
开平方,得,
解得,.
(2) 整理,得,
分解因式,得,
可得或,
解得,.
17.(1) 解:,,
;
.
(2) ;
.
解:(1)证明:∵,
,
∵,
∴
∴不论取何实数,该方程都有两个不相等的实数根;
(2)将代入方程得:,
解得,将代入方程,整理可得:,
解得=1,=-,
∴该方程的另一个根-.
19.(1) ;
(2) 解:抽取的八年级学生成绩的平均数(分)
(3) 七年级的学生对航天航空知识掌握更好.理由如下:
两个年级的平均数相同,但七年级的中位数和众数均高于八年级, 七年级的学生对航天航空知识掌握更好.
20.(1) 证明: 四边形是平行四边形,
,.
,分别是,的平分线,
,,
.
,,,
, 四边形是平行四边形.
,
四边形是菱形.
(2) 解:连接,如答图.
第20题答图
四边形是平行四边形,,,
平分,,,
,是等边三角形,
,边上的高为.
由(1)知四边形是菱形,
,,
.
21.(1) 证明: 四边形是菱形,
,.
,,即,.
, 四边形是平行四边形.
, , 四边形是矩形.
(2) 解: 四边形是菱形,
,,.
,.
在中,由勾股定理,可得
,
.
,
,.
22.(1) 解:.
(2) 根据题意,得,
整理,得,
解得,.
,,
路面设置的宽度符合要求.
(3) 设每平方米草莓平均利润下调元.
根据题意,得,
整理,得,
解得,.
又 要让利于顾客,.
答:每平方米草莓平均利润降低40元.
23.(1) 正方形; ;
(2) 解:.理由如下:
如答图①,将顺时针旋转 得到.
第23题答图①
由旋转的性质,可得,,,.
四边形为正方形,
,
,
,
即,,三点在同一直线上.
由(1)中结论可得 ,
, ,
.
在和中,
,,,
,.
,.
(3) 如答图②,将绕点顺时针旋转 得到,连接.
第23题答图②
根据旋转的性质,可得 ,.
由(2)中的结论可证,
, ,
.
在中,,
,即,
.
[时量:120分钟 分值:150分]
一、选择题(本大题共12个小题,每小题3分,共36分)
1.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
2.如图,小张想估测被池塘隔开的,两处景观之间的距离,他先在外取一点,然后步测出,的中点,,并步测出的长约为,由此估测,之间的距离为( )
第2题图
A. B. C. D.
3.下列说法错误的是( )
A.对角线互相垂直且相等的平行四边形是正方形
B.对角线互相垂直平分的四边形是菱形
C.对角线相等的四边形是矩形
D.对角线互相平分的四边形是平行四边形
4.已知,则的值为( )
A. B. C.2 024 D.2 025
5.某品牌女运动鞋专卖店,老板统计了一周内不同鞋码运动鞋的销售量如表:
鞋码 36 37 38 39 40
平均每天销售量/双 10 12 20 12 12
如果每双鞋的利润相同,你认为老板最关注的销售数据是下列统计量中的( )
A.平均数 B.中位数 C.众数 D.方差
6.若关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B.且
C.且 D.
7.如图,是坐标原点,菱形的顶点在轴的负半轴上,顶点的坐标为,则顶点的坐标为( )
第7题图
A. B. C. D.
8.如图,在中, ,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为,,.若,则图中阴影部分的面积为( )
第8题图
A.6 B. C.5 D.
9.如图,在中,,是的中点,作,垂足在线段上,连接,.下列结论错误的是( )
第9题图
A. B.
C. D.
10.如图,为等腰直角三角形,,以斜边为直角边作等腰直角三角形,再以斜边为直角边作等腰直角三角形, ,按此规律作下去,则的长度为( )
第10题图
A. B. C. D.
二、填空题(本大题共4个小题,每小题5分,共20分)
11.已知一组数据3,6,,2,5,4的众数为5,则这组数据的中位数为____________.
12.如图,已知四边形是菱形,对角线,交于点, ,以点为圆心,长为半径作圆弧交线段于点,则的度数为____________.
第16题图
13.深受人们喜爱的蜘蛛侠代表了善良、正义且具备超能力的艺术形象.如图是某部动作电影中的一座长方体建筑,其底面为正方形,现已知,,蜘蛛侠欲从点开始沿着该建筑的表面环绕长方体建筑1圈,最后到达点处,则蜘蛛侠行走的最短距离为____________.
第17题图
14.如图,在矩形中,,,延长到点,使,连接,动点从点出发,以每秒2个单位的速度沿向终点运动.设点的运动时间为,当的值为____________时,与全等.
三、解答题(本大题共9个小题,共90分)
15.(8分)计算:
(1) ;
(2) .
16.(8分)解下列方程:
(1) (用配方法);
(2) .
17.(10分)设,.
(1) 求,的值;
(2) 求,的值.
18. (8分)已知关于的方程.
(1)求证:不论取任何实数,该方程总有两个不相等的实数根;
(2)若该方程的一个根为,求的值及该方程的另一个根.
19.(10分)4月24日是中国航天日,为激发青少年崇尚科学、探索未知的热情,某中学开展“航空航天”知识问答系列活动.为了解活动效果,从七、八年级学生的知识问答成绩中,各随机抽取了20名学生的成绩进行统计分析(6分及6分以上为合格:9分及9分以上为优秀),绘制了如下统计图表:
学生成绩统计表
统计量 七年级 八年级
平均数 7.55
中位数 8
众数 7
根据上述信息,解答下列问题:
(1) 学生成绩统计表中________,____________.
(2) 求抽取的八年级学生成绩的平均数.
(3) 根据以上数据,你认为该校七、八年级中哪个年级的学生对航空航天知识掌握更好?并说明理由.
20.(10分)如图,在中,,分别是,的平分线,且,分别在边,上,.
(1) 求证:四边形是菱形;
(2) 若 ,,求的面积.
21.(12分)如图,在菱形中,对角线,交于点,过点作的垂线,垂足为,延长到点,使,连接.
(1) 求证:四边形是矩形;
(2) 若,,求的长.
22.(12分)根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材1 某农户承包了一块矩形果园,如图是果园的平面图,其中,.准备在它的四周铺设道路,上、下两条横向道路的宽度都为,左、右两条纵向道路的宽度都为,中间部分种植水果.出于货车通行等因素的考虑,道路宽度不超过,且不小于.
素材2 该农户发现某一种草莓销售前景比较不错,经市场调查,草莓培育一年可产果,若每平方米的草莓销售平均利润为100元,每月可销售的草莓.受天气原因,农户为了快速将草莓出手,决定降价.若每平方米草莓平均利润下调5元,每月可多销售草莓.果园每月的承包费为2万元.
问题解决
任务1
解决果园中路面宽度的设计对种植面积的影响.
(1) 请直接写出的取值范围.
(2) 若中间种植的面积是,路面设置的宽度是否符合要求
任务2
解决果园种植的预期利润问题.
(总利润销售利润-承 包费)
(3) 若农户预期一个月的总利润为52万元,从购买草莓客户的角度考虑,每平方米草平均利润应该降低多少元?
23.(14分)综合与实践
综合与实践课上,老师让同学们以“图形的折叠与变换”为主题开展数学活动.
(1) 【操作判断】
操作一:如图①,将矩形纸片折叠,使落在边上,点与点重合,折痕为.
根据以上操作:四边形的形状是________.
操作二:沿剪开,将四边形折叠,使边,都落在四边形的对角线上,折痕为,,连接,如图②.
根据以上操作:的度数为____________;线段,,的数量关系是__________________.
(2) 【迁移探究】
如图③,在,上分别取点,,使和图②中的度数相等,连接,探究线段,,之间的数量关系,并说明理由.
(3) 【拓展应用】
在(2)的探究下,连接对角线,若图③中的的边,分别交对角线于点,,将纸片沿对角线剪开,如图④,若,,求出的长.
期末质量评估
一、选择题(本大题共10个小题,每小题4分,共40分)
1.B 2.C 3.C 4.B 5.C 6.B 7.C 8.B 9.D 10.B
二、填空题(本大题共4个小题,每小题5分,共20分)
11.
12.
13.
14.或7
三、解答题(本大题共9个小题,共90分)
15.(1) 解:原式.
(2) 原式.
16.(1) 解:整理,得,
配方,得,即,
开平方,得,
解得,.
(2) 整理,得,
分解因式,得,
可得或,
解得,.
17.(1) 解:,,
;
.
(2) ;
.
解:(1)证明:∵,
,
∵,
∴
∴不论取何实数,该方程都有两个不相等的实数根;
(2)将代入方程得:,
解得,将代入方程,整理可得:,
解得=1,=-,
∴该方程的另一个根-.
19.(1) ;
(2) 解:抽取的八年级学生成绩的平均数(分)
(3) 七年级的学生对航天航空知识掌握更好.理由如下:
两个年级的平均数相同,但七年级的中位数和众数均高于八年级, 七年级的学生对航天航空知识掌握更好.
20.(1) 证明: 四边形是平行四边形,
,.
,分别是,的平分线,
,,
.
,,,
, 四边形是平行四边形.
,
四边形是菱形.
(2) 解:连接,如答图.
第20题答图
四边形是平行四边形,,,
平分,,,
,是等边三角形,
,边上的高为.
由(1)知四边形是菱形,
,,
.
21.(1) 证明: 四边形是菱形,
,.
,,即,.
, 四边形是平行四边形.
, , 四边形是矩形.
(2) 解: 四边形是菱形,
,,.
,.
在中,由勾股定理,可得
,
.
,
,.
22.(1) 解:.
(2) 根据题意,得,
整理,得,
解得,.
,,
路面设置的宽度符合要求.
(3) 设每平方米草莓平均利润下调元.
根据题意,得,
整理,得,
解得,.
又 要让利于顾客,.
答:每平方米草莓平均利润降低40元.
23.(1) 正方形; ;
(2) 解:.理由如下:
如答图①,将顺时针旋转 得到.
第23题答图①
由旋转的性质,可得,,,.
四边形为正方形,
,
,
,
即,,三点在同一直线上.
由(1)中结论可得 ,
, ,
.
在和中,
,,,
,.
,.
(3) 如答图②,将绕点顺时针旋转 得到,连接.
第23题答图②
根据旋转的性质,可得 ,.
由(2)中的结论可证,
, ,
.
在中,,
,即,
.
同课章节目录
