2024-2025学年北师大版九年级数学下册第二章二次函数复习题课件(共80张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册第二章二次函数复习题课件(共80张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 15:52:19 | ||
图片预览










文档简介
(共80张PPT)
复习题
北师版·九年级下册
1. 两个数的和为6,这两个数的积最大可以达到多少?利用图象描述乘积与因数之间的关系.
2. 求下列二次函数图象的对称轴和顶点坐标:
(1)y = 2-2x2; (2)y = -3(x-1) 2+5;
(3)y = 4(x+3) 2-1; (4)y = x(5-x) ;
(5)y =1+2x-x2; (6)y = 2x2-7x+12.
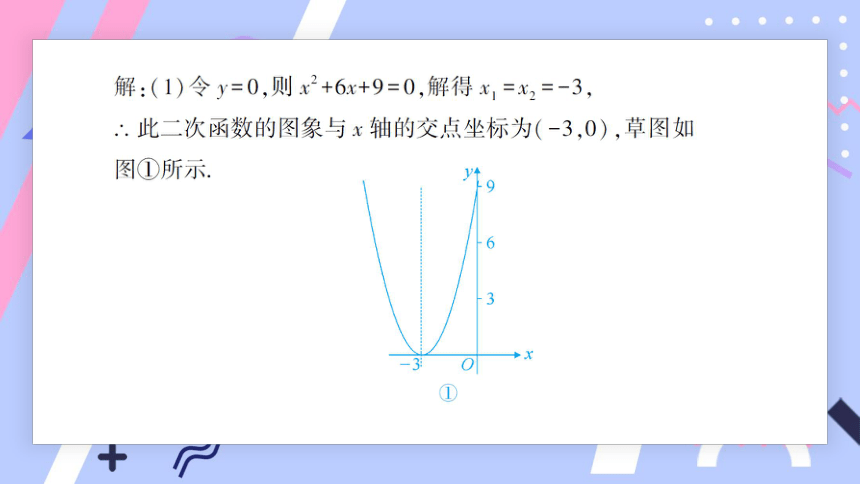
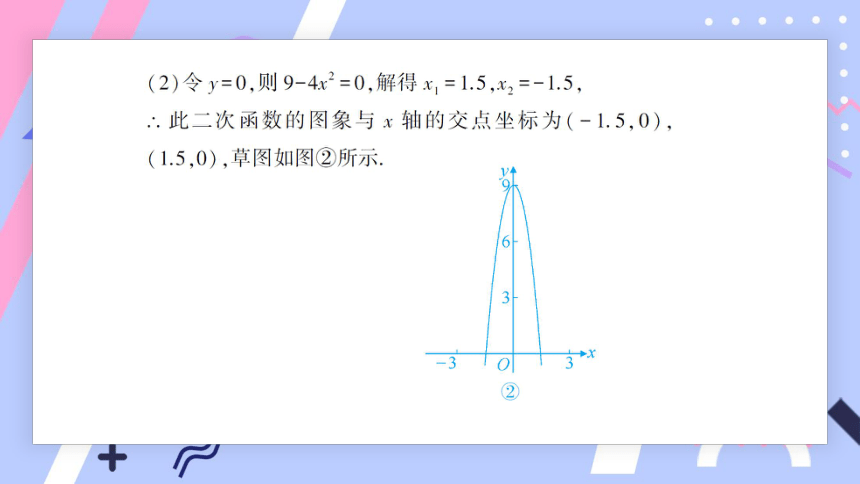
3.求下列二次函数的图象与x轴的交点的坐标,并画草图验证:
(1)y = x2+6x+9; (2)y = 9-4x2;
(3)y = (x+1) 2-9.
成才路
4. 把一根长120 cm的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积和最小是多少?
成才路
成才路
5.当运动中的汽车撞到物体时,汽车所受到的损坏程度可以用“撞击影响”来衡量.某型汽车的撞击影响可以用公式 I = 2v2 来表示,其中v ( km/min)表示汽车的速度.
(1)列表表示I与v的关系;
(2)当汽车的速度增加到原来的2倍时,撞击影响扩大为原来的多少倍
成才路
成才路
6. 自由落体运动是由于引力的作用而造成的,地球上物体自由下落的时间t (s)和下落的距离h (m)的关系是h=4.9t2.我们知道,对同一物体,月球的引力大约是地球引力的 ,因此月球上物体自由下落的时间t (s)和下落的距离h (m)的关系大约是h=0.8t2.
(1)在同一直角坐标系中画图,分别表示地球、月球上h和t的关系;
(2)比较物体下落4s时,在地球上和月球上分别下落的距离;
(3)比较物体下落10m时,在地球上和月球上分别所需要的时间(结 果精确到0.1s).
成才路
成才路
7.求二次函数y=x2-x-5的图象与一次函数y=2x-1的图象的交点坐标. 请利用函数表达式、表格和图象三种方法求解.
成才路
成才路
8. 方程-x2+2x+ = 0的根与二次函数y =-x2+2x+ 的图象之间有什么关系
成才路
成才路
9. 利用二次函数的图象求下列一元二次方程的近似根:
(1)x2 +11x = 9; (2)x2 + 3x = 20;
(3)x2 + 2x -9= 0; (4)x2+3 = 3x.
成才路
成才路
10.写出等边三角形的面积S与其边长a之间的关系式,并分别计算当a=1, ,2时三角形的面积.
成才路
成才路
11.正方形的边长是x,面积是A,周长是l.
(1)分别写出A,l与x的关系式;
(2)在同一直角坐标系中画出(1)中两个函数的图象,比较它们的变化趋势;
(3)你所画的函数A = x2的图象与函数y = x2的图象有什么不同?为什么?
成才路
成才路
12. 已知平行四边形的高与底边的比是h∶a=2∶5,用表达式表示平行四边形的面积S与它的底边a的关系,并从图象观察平行四边形的面积随其底边的变化而变化的情况.
成才路
成才路
13. 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数 y = 4x- x2刻画,斜坡可以用一次函数 y = x 刻画.
(1)求小球到达的最高点的坐标;
(2)小球的落点是A,求点A的坐标.
成才路
成才路
14. 如图,假设篱笆(虚线部分)的长度是15 m,如何围篱笆才能使其所围矩形的面积最大 最大面积是多少
成才路
成才路
15.如图(单位:m),等腰直角三角形ABC以2m/s的速度沿直线l向正方形移动,直到AB与CD重合.设x s时,三角形与正方形重叠部分的面积为y m2.
(1)写出y与x的关系式;
(2)当x=2,3.5时,y分别是多少
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间
成才路
成才路
16. 科研人员在测试一枚火箭向上竖直升空时,获得火箭的高度h(m)与时间t(s)的关系数据如下:
时间t/s 1 5 10 15 20 25
火箭高度h/m 155 635 1010 1135 1010 635
(1)根据上表,以时间t为横轴、高度h为纵轴建立直角坐标系,并描出上述各点.
时间t/s 1 5 10 15 20 25
火箭高度h/m 155 635 1010 1135 1010 635
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗
(3)你能确定h关于t的函数表达式吗
(4)你能求出该火箭的最高射程是多少吗 你是根据哪种表示方式求解的
成才路
成才路
17.如图,喷水池的喷水口位于水池中心,离水面高为0.5m,喷出的水流呈抛物线形状,最高点离水面 m,落水点离池中心1 m.
请建立适当的直角坐标系,用函数表达式描述左右两边的两条水流,并说明自变量的取值范围.
成才路
成才路
18. 把一个数a拆成两数之和,何时它们的乘积最大 你能得出一个一般性的结论吗
成才路
成才路
19. 相框边的宽窄影响可放入相片的大小.如图,相框长26 cm,宽22 cm,相框边的宽 x cm,相框内的面积为y cm2.
(1)写出y与x的函数关系式;
(2)画出这个函数的图象;
(3)当x =1,1.5,2时,分别可以放入多大的相片
成才路
成才路
20.竖直向上发射的物体的高度h(m)满足关系式h = -5t2+ v0t,其中t (s)是物体运动的时间,v0 ( m/s)是物体被发射时的速度. 某公园计划设计园内喷泉,喷水的最大高度要求达到15m,喷水的速度应该达到多少 (结果精确到0.01 m/s )
成才路
成才路
21.如图,隧道的截面由抛物线和长方形构成.长方形的长为16 m,宽为6 m,抛物线的最高点C离路面AA1的距离为8 m.
(1)按如图所示的直角坐标系,求表示
该抛物线的函数表达式;
(2)一大型货运汽车装载某大型设备后
高为7m,宽为4m.如果该隧道内设双向行车道,那么这辆货车能否安全通过
成才路
成才路
22. 一座抛物线型拱桥如图所示,桥下水面宽度是4m时,拱顶到水面的距离是2m.当水面下降1m后,水面宽度是多少 (结果精确到0.1 m)
成才路
成才路
23. 如图,在△ABC中,AB= AC= 10,BC=12. 在△ABC中截出一个矩形DEFG,其中D,G分别在AB和AC边上,EF在BC边上.设EF=x,矩形DEFG的面积为y,写出y与x之间的函数关系式,列出表格,并画出相应的函数图象. 根据三种表示方法回答下列问题:
(1)自变量x的取值范围是什么?
(2)图象的对称轴和顶点坐标分别是什么?
(3)你能描述y随x的变化而变化的情况吗?
成才路
成才路
24. 某种蔬菜的销售单价与销售月份之间的关系如图(1)所示,成本与销售月份之间的关系如图(2)所示(图(1)的图象是线段,图(2)的图象是抛物线)哪个月出售这种蔬菜,每千克的收益最大 (收益=售价―成本)
成才路
成才路
25. (1)如图,第n个图形中有多少个小正方形?你是如何计算的?
(2)求1+3,1+3+5,1+3+5+7,1+3+5+7+9,···,1+3+5+7+9+…+(2n-1).
成才路
成才路
26. (1)你知道下面每一个图形中各有多少个小圆圈吗?第6个图形中应该有多少个小圆圈?为什么?
(2)完成下表:
边上的小圆圈数 1 2 3 4 5
每个图中小圆圈的总数
1
3
6
10
15
(3)如果用n表示等边三角形边上的小圆圈数,m表示这个三角形中小圆圈的总数,那么m和n的关系是什么
27. (1)你知道下面每一个图形中各有多少个小圆圈吗?第5个图形中应该有多少个小圆圈?为什么?
(2)完成下表:
边上的小圆圈数 1 2 3 4 5
每个图中小圆圈的总数
1
7
19
37
61
(3)如果用n表示六边形边上的小圆圈数,m表示这个六边形中小圆圈的总数,那么m和n的关系是什么
28. 求如图所示的图形中小圆圈的总数.
复习题
北师版·九年级下册
1. 两个数的和为6,这两个数的积最大可以达到多少?利用图象描述乘积与因数之间的关系.
2. 求下列二次函数图象的对称轴和顶点坐标:
(1)y = 2-2x2; (2)y = -3(x-1) 2+5;
(3)y = 4(x+3) 2-1; (4)y = x(5-x) ;
(5)y =1+2x-x2; (6)y = 2x2-7x+12.
3.求下列二次函数的图象与x轴的交点的坐标,并画草图验证:
(1)y = x2+6x+9; (2)y = 9-4x2;
(3)y = (x+1) 2-9.
成才路
4. 把一根长120 cm的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积和最小是多少?
成才路
成才路
5.当运动中的汽车撞到物体时,汽车所受到的损坏程度可以用“撞击影响”来衡量.某型汽车的撞击影响可以用公式 I = 2v2 来表示,其中v ( km/min)表示汽车的速度.
(1)列表表示I与v的关系;
(2)当汽车的速度增加到原来的2倍时,撞击影响扩大为原来的多少倍
成才路
成才路
6. 自由落体运动是由于引力的作用而造成的,地球上物体自由下落的时间t (s)和下落的距离h (m)的关系是h=4.9t2.我们知道,对同一物体,月球的引力大约是地球引力的 ,因此月球上物体自由下落的时间t (s)和下落的距离h (m)的关系大约是h=0.8t2.
(1)在同一直角坐标系中画图,分别表示地球、月球上h和t的关系;
(2)比较物体下落4s时,在地球上和月球上分别下落的距离;
(3)比较物体下落10m时,在地球上和月球上分别所需要的时间(结 果精确到0.1s).
成才路
成才路
7.求二次函数y=x2-x-5的图象与一次函数y=2x-1的图象的交点坐标. 请利用函数表达式、表格和图象三种方法求解.
成才路
成才路
8. 方程-x2+2x+ = 0的根与二次函数y =-x2+2x+ 的图象之间有什么关系
成才路
成才路
9. 利用二次函数的图象求下列一元二次方程的近似根:
(1)x2 +11x = 9; (2)x2 + 3x = 20;
(3)x2 + 2x -9= 0; (4)x2+3 = 3x.
成才路
成才路
10.写出等边三角形的面积S与其边长a之间的关系式,并分别计算当a=1, ,2时三角形的面积.
成才路
成才路
11.正方形的边长是x,面积是A,周长是l.
(1)分别写出A,l与x的关系式;
(2)在同一直角坐标系中画出(1)中两个函数的图象,比较它们的变化趋势;
(3)你所画的函数A = x2的图象与函数y = x2的图象有什么不同?为什么?
成才路
成才路
12. 已知平行四边形的高与底边的比是h∶a=2∶5,用表达式表示平行四边形的面积S与它的底边a的关系,并从图象观察平行四边形的面积随其底边的变化而变化的情况.
成才路
成才路
13. 如图,一小球从斜坡O点处抛出,球的抛出路线可以用二次函数 y = 4x- x2刻画,斜坡可以用一次函数 y = x 刻画.
(1)求小球到达的最高点的坐标;
(2)小球的落点是A,求点A的坐标.
成才路
成才路
14. 如图,假设篱笆(虚线部分)的长度是15 m,如何围篱笆才能使其所围矩形的面积最大 最大面积是多少
成才路
成才路
15.如图(单位:m),等腰直角三角形ABC以2m/s的速度沿直线l向正方形移动,直到AB与CD重合.设x s时,三角形与正方形重叠部分的面积为y m2.
(1)写出y与x的关系式;
(2)当x=2,3.5时,y分别是多少
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间
成才路
成才路
16. 科研人员在测试一枚火箭向上竖直升空时,获得火箭的高度h(m)与时间t(s)的关系数据如下:
时间t/s 1 5 10 15 20 25
火箭高度h/m 155 635 1010 1135 1010 635
(1)根据上表,以时间t为横轴、高度h为纵轴建立直角坐标系,并描出上述各点.
时间t/s 1 5 10 15 20 25
火箭高度h/m 155 635 1010 1135 1010 635
(2)你能根据坐标系中各点的变化趋势确定h关于t的函数类型吗
(3)你能确定h关于t的函数表达式吗
(4)你能求出该火箭的最高射程是多少吗 你是根据哪种表示方式求解的
成才路
成才路
17.如图,喷水池的喷水口位于水池中心,离水面高为0.5m,喷出的水流呈抛物线形状,最高点离水面 m,落水点离池中心1 m.
请建立适当的直角坐标系,用函数表达式描述左右两边的两条水流,并说明自变量的取值范围.
成才路
成才路
18. 把一个数a拆成两数之和,何时它们的乘积最大 你能得出一个一般性的结论吗
成才路
成才路
19. 相框边的宽窄影响可放入相片的大小.如图,相框长26 cm,宽22 cm,相框边的宽 x cm,相框内的面积为y cm2.
(1)写出y与x的函数关系式;
(2)画出这个函数的图象;
(3)当x =1,1.5,2时,分别可以放入多大的相片
成才路
成才路
20.竖直向上发射的物体的高度h(m)满足关系式h = -5t2+ v0t,其中t (s)是物体运动的时间,v0 ( m/s)是物体被发射时的速度. 某公园计划设计园内喷泉,喷水的最大高度要求达到15m,喷水的速度应该达到多少 (结果精确到0.01 m/s )
成才路
成才路
21.如图,隧道的截面由抛物线和长方形构成.长方形的长为16 m,宽为6 m,抛物线的最高点C离路面AA1的距离为8 m.
(1)按如图所示的直角坐标系,求表示
该抛物线的函数表达式;
(2)一大型货运汽车装载某大型设备后
高为7m,宽为4m.如果该隧道内设双向行车道,那么这辆货车能否安全通过
成才路
成才路
22. 一座抛物线型拱桥如图所示,桥下水面宽度是4m时,拱顶到水面的距离是2m.当水面下降1m后,水面宽度是多少 (结果精确到0.1 m)
成才路
成才路
23. 如图,在△ABC中,AB= AC= 10,BC=12. 在△ABC中截出一个矩形DEFG,其中D,G分别在AB和AC边上,EF在BC边上.设EF=x,矩形DEFG的面积为y,写出y与x之间的函数关系式,列出表格,并画出相应的函数图象. 根据三种表示方法回答下列问题:
(1)自变量x的取值范围是什么?
(2)图象的对称轴和顶点坐标分别是什么?
(3)你能描述y随x的变化而变化的情况吗?
成才路
成才路
24. 某种蔬菜的销售单价与销售月份之间的关系如图(1)所示,成本与销售月份之间的关系如图(2)所示(图(1)的图象是线段,图(2)的图象是抛物线)哪个月出售这种蔬菜,每千克的收益最大 (收益=售价―成本)
成才路
成才路
25. (1)如图,第n个图形中有多少个小正方形?你是如何计算的?
(2)求1+3,1+3+5,1+3+5+7,1+3+5+7+9,···,1+3+5+7+9+…+(2n-1).
成才路
成才路
26. (1)你知道下面每一个图形中各有多少个小圆圈吗?第6个图形中应该有多少个小圆圈?为什么?
(2)完成下表:
边上的小圆圈数 1 2 3 4 5
每个图中小圆圈的总数
1
3
6
10
15
(3)如果用n表示等边三角形边上的小圆圈数,m表示这个三角形中小圆圈的总数,那么m和n的关系是什么
27. (1)你知道下面每一个图形中各有多少个小圆圈吗?第5个图形中应该有多少个小圆圈?为什么?
(2)完成下表:
边上的小圆圈数 1 2 3 4 5
每个图中小圆圈的总数
1
7
19
37
61
(3)如果用n表示六边形边上的小圆圈数,m表示这个六边形中小圆圈的总数,那么m和n的关系是什么
28. 求如图所示的图形中小圆圈的总数.
