九年级上册期末综合复习题2(含答案)2024-2025学年人教版数学
文档属性
| 名称 | 九年级上册期末综合复习题2(含答案)2024-2025学年人教版数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 00:00:00 | ||
图片预览



文档简介
九年级上册数学人教版期末综合复习题2
一、单选题(每小题3分,共30分)
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,如图四幅作品分别代表“立春”,“立夏”“芒种”“大雪”,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.方程的两根为、,则( )
A.6 B. C.3 D.
3.下列所给方程中,没有实数根的是( )
A. B.
C. D.
4.当时,函数的最小值为1,则a的值为( )
A.0 B.2 C.0或2 D.0或3
5.如图,正方形的顶点、在抛物线上,点在轴上.若、两点的横坐标分别为、,下列结论正确的是( )
A. B. C. D.
6.如图,点A,B,C在上,的切线交的延长线于D,若,则的度数为( )
A. B. C. D.
7.点与点关于原点对称,则的值为( )
A. B.1 C. D.2024
8.如图,在中, ,是的内切圆,三个切点分别为,,,若,,则的面积是( )
A. B. C. D.
9.在一个不透明的纸箱中,内有蓝色、红色的玻璃球共20个,这些玻璃球除颜色外都相同.小何每次摸出一个球后放回,通过多次摸球试验后发现摸到蓝色玻璃球的频率稳定在,则纸箱中蓝色玻璃球很可能有( )
A.5个 B.10个 C.15个 D.16个
10.如图,这是某运动员在单板滑雪大跳台中的高度与运动时间的运动路线图的一部分,运动员起跳后的运动路线可以近似地看作抛物线的一部分,其中线段表示跳台的高度,,为该运动员在空中到达的最大高度,若该运动员运动到空中点Q时,点Q的坐标为,则该运动员在空中到达的最大高度的长为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.若是一元二次方程的一个根,则 .
12.已知、是的两个根,则的值为
13.平面直角坐标系中,若平移二次函数的图象,使其与x轴交于两点,且此两点的距离为1个单位,则平移方式为 .
14.如图,二次函数的图象与一次函数的图象交于点,,则不等式的解集是 .
15.如图,在正方形中,.,E为边上一点,点F在边上,且,将点E绕着点F顺时针旋转得到点G,连接,则的长的最小值为 .
16.如图,在中,,截三边所得的弦长相等,则的度数是 .
17.如图,直角中,,以A为圆心,长为半径画四分之一圆,则图中阴影部分的面积是
18.不透明的袋子中装有若干个除颜色外完全相同的小球(没有粉色),实验小组向其中投入10个除颜色外无其他差别的粉色小球.摸出一个球,记录颜色,放回混合均匀,再摸出一个球,记录颜色,重复多次,发现摸到粉色小球的频率稳定在0.02附近,可以估计袋子中原来有 个小球.
三、解答题
19.解方程∶(每小题4分,共8分)
(1)(用公式法); (2).
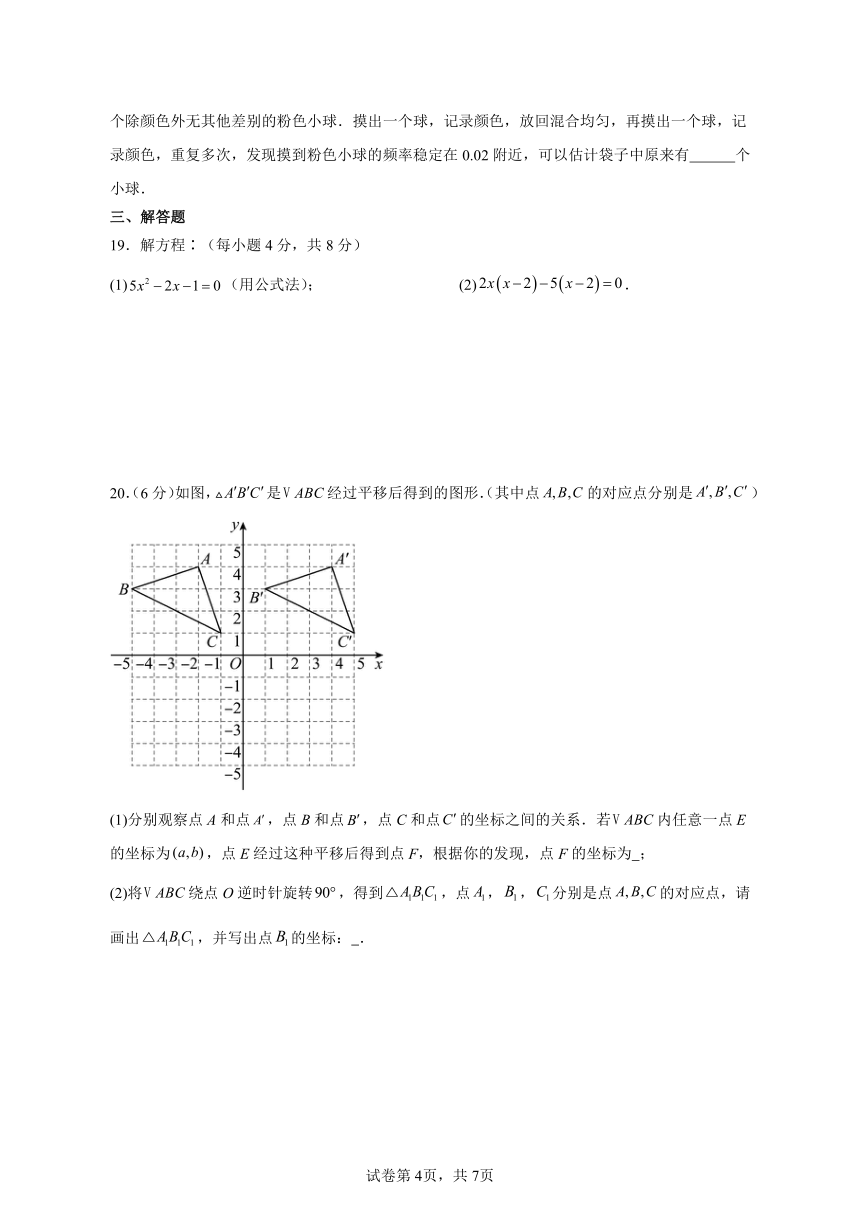
20.(6分)如图,是经过平移后得到的图形.(其中点的对应点分别是)
(1)分别观察点A和点,点B和点,点C和点的坐标之间的关系.若内任意一点E的坐标为,点E经过这种平移后得到点F,根据你的发现,点F的坐标为 ;
(2)将绕点O逆时针旋转,得到,点,,分别是点的对应点,请画出,并写出点的坐标: .
21.(6分)已知关于x的一元二次方程.求证:无论k取何值,该方程总有两个实数根.
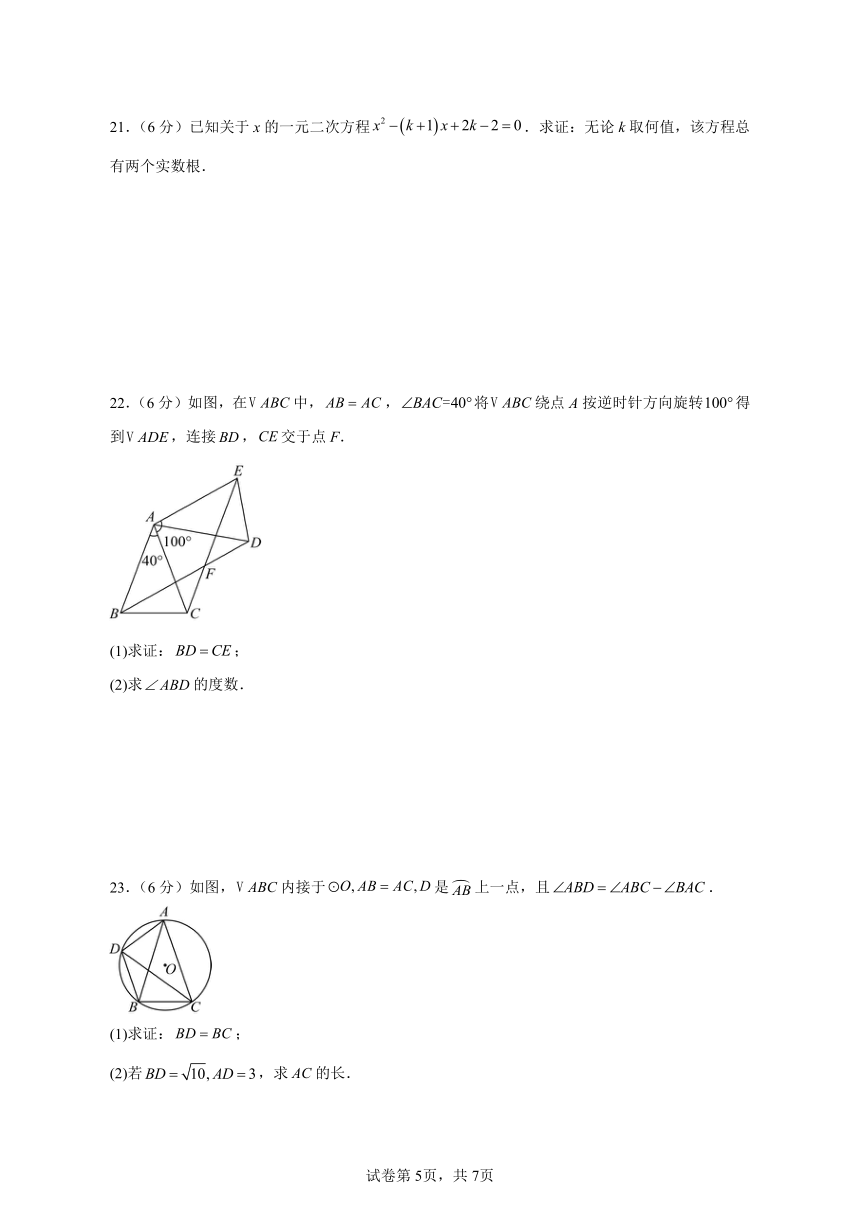
22.(6分)如图,在中,,将绕点A按逆时针方向旋转得到,连接,交于点F.
(1)求证:;
(2)求的度数.
23.(6分)如图,内接于是上一点,且.
(1)求证:;
(2)若,求的长.
24.(8分)如图,是的直径,P为的中点,连接并延长至点B,使,连接.
(1)求证为的切线;
(2)若,求图中阴影部分的面积.
25.(8分)某种规格的梭子蟹养殖成本为30元/千克,根据市场调查发现,售价为50元/千克时,每天可销售400千克,为增大市场占有率,在保证盈利的情况下,养殖户采取降价措施,梭子蟹的售价每降低1元,每天销量可增加40千克.
(1)当售价降低2元时,养殖户每天可销售 千克梭子蟹;
(2)若养殖户每天的利润要达到8840元,并尽可能让利顾客,则售价应降低多少元?
26.(8分)李明同学的不透明袋子中有四张除数字外完全相同的卡片,四张卡片上分别标有数字,,,,王华同学的不透明袋子中有三张除数字外完全相同的卡片,三张卡片上分别标有数字,,.张老师先从李明同学的袋子中随机取出一张卡片,再从王华同学的袋子中随机取出一张卡片,分别用、表示张老师从李明、王华袋子中抽出的卡片上标有的数字.
(1)请用画树状图法或列表法写出所有等可能的结果;
(2)求抽出的能使关于的一元二次方程有实数根的概率.
27.(10分)如图,抛物线与轴交于、两点(点在点的左侧),点的坐标为,与轴交于点,作直线.动点在轴上运动,过点作轴,交抛物线于点,交直线于点,设点的横坐标为.
(1)(2分)求抛物线的解析式和直线的解析式;
(2)(2分)当点在线段上运动时,求线段的最大值;
(3)(3分)当点在线段上运动时,若是以为腰的等腰直角三角形时,求的值;
(4)(3分)当以、、、为顶点的四边形是平行四边形时,直接写出的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C D A B B A A D
11.2025
12.
13.向下平移4个单位长度
14.
15.8
16.
17.
18.
19.(1)解:,,,
∴,
∴,
∴,;
(2)解:,
∴,
∴或,
∴,.
20.(1)解:观察图形的变化发现:平移后的三角形的三个点的横坐标加,纵坐标不变,
∴点F的坐标为:,
故答案为:;
(2)解:如图,即为所求;
点的坐标为,
故答案为:.
21.解:
.
∵,
∴,
∴无论k取何值,该方程总有两个实数根.
22.(1)证明:∵将绕点A按逆时针方向旋转得到,
∴,,,
∵,
∴,
在和中,
,
∴,
∴;
(2)解:由(1)知,,,
∴是等腰三角形,
∴,
∴的度数为.
23.(1)证明:,
,
,
,
,
;
(2)解:延长到点E,使,连接,过点B作于点F.如图所示:
∵四边形内接于,
,
,
,
,
设
∵,
.
在和中,
,
(舍去),
.
24.(1)证明:∵是的直径,
∴,
∵P为的中点,
∴,
∴,
∵,
∴,
∴,
∴,
∴为的切线;
(2)解:∵,
∴,,
∵P为的中点,
∴,
∴
25.(1)解:设养殖户每天的销量y千克,降价x元,依题意得函数关系为,
当时,,
∴当售价降低2元时,养殖户每天可销售480千克梭子蟹;
故答案为:480;
(2)解:依题意得:,
整理得:,
解得:,,
又∵要尽可能让利顾客,
∴,
答:售价应降低7元.
26.(1)解:画树状图如下:
所有可能情况为:,,,,,,,,,,,.
(2)解:∵一元二次方程有实数根,
∴,
整理可得:,
∴适合的有,,共个,
所以,.
27.(1)解:∵抛物线过、两点,
∴代入抛物线解析式可得,
解得,
∴抛物线解析式为,
令可得,,解,
∵点在点右侧,
∴点坐标为,
设直线解析式为,
把、坐标代入可得,解得,
∴直线解析式为;
(2)解:∵轴,点的横坐标为,
∴,,
∵在线段上运动,
∴点在点上方,
∴,
∴当时,有最大值,的最大值为;
(3)解:由(1)(2)得点坐标为,点坐标为,
∴
∵
∴
∵轴,轴,
∴
∴
∴当是以为腰的等腰直角三角形时,,
∴点纵坐标为,
∴,解得或,
当时,则、重合,不能构成三角形,不符合题意,舍去,
∴;
(4)解:由()得,,
当以、、、为顶点的四边形是平行四边形时,则有,
当点在线段上时,由()得,
∴,此方程无实数根,
当点不在线段上时,则有,
∴,解得或,
综上可知当以、、、为顶点的四边形是平行四边形时,的值为或.
答案第1页,共2页
答案第1页,共2页
一、单选题(每小题3分,共30分)
1.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,如图四幅作品分别代表“立春”,“立夏”“芒种”“大雪”,其中既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.方程的两根为、,则( )
A.6 B. C.3 D.
3.下列所给方程中,没有实数根的是( )
A. B.
C. D.
4.当时,函数的最小值为1,则a的值为( )
A.0 B.2 C.0或2 D.0或3
5.如图,正方形的顶点、在抛物线上,点在轴上.若、两点的横坐标分别为、,下列结论正确的是( )
A. B. C. D.
6.如图,点A,B,C在上,的切线交的延长线于D,若,则的度数为( )
A. B. C. D.
7.点与点关于原点对称,则的值为( )
A. B.1 C. D.2024
8.如图,在中, ,是的内切圆,三个切点分别为,,,若,,则的面积是( )
A. B. C. D.
9.在一个不透明的纸箱中,内有蓝色、红色的玻璃球共20个,这些玻璃球除颜色外都相同.小何每次摸出一个球后放回,通过多次摸球试验后发现摸到蓝色玻璃球的频率稳定在,则纸箱中蓝色玻璃球很可能有( )
A.5个 B.10个 C.15个 D.16个
10.如图,这是某运动员在单板滑雪大跳台中的高度与运动时间的运动路线图的一部分,运动员起跳后的运动路线可以近似地看作抛物线的一部分,其中线段表示跳台的高度,,为该运动员在空中到达的最大高度,若该运动员运动到空中点Q时,点Q的坐标为,则该运动员在空中到达的最大高度的长为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.若是一元二次方程的一个根,则 .
12.已知、是的两个根,则的值为
13.平面直角坐标系中,若平移二次函数的图象,使其与x轴交于两点,且此两点的距离为1个单位,则平移方式为 .
14.如图,二次函数的图象与一次函数的图象交于点,,则不等式的解集是 .
15.如图,在正方形中,.,E为边上一点,点F在边上,且,将点E绕着点F顺时针旋转得到点G,连接,则的长的最小值为 .
16.如图,在中,,截三边所得的弦长相等,则的度数是 .
17.如图,直角中,,以A为圆心,长为半径画四分之一圆,则图中阴影部分的面积是
18.不透明的袋子中装有若干个除颜色外完全相同的小球(没有粉色),实验小组向其中投入10个除颜色外无其他差别的粉色小球.摸出一个球,记录颜色,放回混合均匀,再摸出一个球,记录颜色,重复多次,发现摸到粉色小球的频率稳定在0.02附近,可以估计袋子中原来有 个小球.
三、解答题
19.解方程∶(每小题4分,共8分)
(1)(用公式法); (2).
20.(6分)如图,是经过平移后得到的图形.(其中点的对应点分别是)
(1)分别观察点A和点,点B和点,点C和点的坐标之间的关系.若内任意一点E的坐标为,点E经过这种平移后得到点F,根据你的发现,点F的坐标为 ;
(2)将绕点O逆时针旋转,得到,点,,分别是点的对应点,请画出,并写出点的坐标: .
21.(6分)已知关于x的一元二次方程.求证:无论k取何值,该方程总有两个实数根.
22.(6分)如图,在中,,将绕点A按逆时针方向旋转得到,连接,交于点F.
(1)求证:;
(2)求的度数.
23.(6分)如图,内接于是上一点,且.
(1)求证:;
(2)若,求的长.
24.(8分)如图,是的直径,P为的中点,连接并延长至点B,使,连接.
(1)求证为的切线;
(2)若,求图中阴影部分的面积.
25.(8分)某种规格的梭子蟹养殖成本为30元/千克,根据市场调查发现,售价为50元/千克时,每天可销售400千克,为增大市场占有率,在保证盈利的情况下,养殖户采取降价措施,梭子蟹的售价每降低1元,每天销量可增加40千克.
(1)当售价降低2元时,养殖户每天可销售 千克梭子蟹;
(2)若养殖户每天的利润要达到8840元,并尽可能让利顾客,则售价应降低多少元?
26.(8分)李明同学的不透明袋子中有四张除数字外完全相同的卡片,四张卡片上分别标有数字,,,,王华同学的不透明袋子中有三张除数字外完全相同的卡片,三张卡片上分别标有数字,,.张老师先从李明同学的袋子中随机取出一张卡片,再从王华同学的袋子中随机取出一张卡片,分别用、表示张老师从李明、王华袋子中抽出的卡片上标有的数字.
(1)请用画树状图法或列表法写出所有等可能的结果;
(2)求抽出的能使关于的一元二次方程有实数根的概率.
27.(10分)如图,抛物线与轴交于、两点(点在点的左侧),点的坐标为,与轴交于点,作直线.动点在轴上运动,过点作轴,交抛物线于点,交直线于点,设点的横坐标为.
(1)(2分)求抛物线的解析式和直线的解析式;
(2)(2分)当点在线段上运动时,求线段的最大值;
(3)(3分)当点在线段上运动时,若是以为腰的等腰直角三角形时,求的值;
(4)(3分)当以、、、为顶点的四边形是平行四边形时,直接写出的值.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C C D A B B A A D
11.2025
12.
13.向下平移4个单位长度
14.
15.8
16.
17.
18.
19.(1)解:,,,
∴,
∴,
∴,;
(2)解:,
∴,
∴或,
∴,.
20.(1)解:观察图形的变化发现:平移后的三角形的三个点的横坐标加,纵坐标不变,
∴点F的坐标为:,
故答案为:;
(2)解:如图,即为所求;
点的坐标为,
故答案为:.
21.解:
.
∵,
∴,
∴无论k取何值,该方程总有两个实数根.
22.(1)证明:∵将绕点A按逆时针方向旋转得到,
∴,,,
∵,
∴,
在和中,
,
∴,
∴;
(2)解:由(1)知,,,
∴是等腰三角形,
∴,
∴的度数为.
23.(1)证明:,
,
,
,
,
;
(2)解:延长到点E,使,连接,过点B作于点F.如图所示:
∵四边形内接于,
,
,
,
,
设
∵,
.
在和中,
,
(舍去),
.
24.(1)证明:∵是的直径,
∴,
∵P为的中点,
∴,
∴,
∵,
∴,
∴,
∴,
∴为的切线;
(2)解:∵,
∴,,
∵P为的中点,
∴,
∴
25.(1)解:设养殖户每天的销量y千克,降价x元,依题意得函数关系为,
当时,,
∴当售价降低2元时,养殖户每天可销售480千克梭子蟹;
故答案为:480;
(2)解:依题意得:,
整理得:,
解得:,,
又∵要尽可能让利顾客,
∴,
答:售价应降低7元.
26.(1)解:画树状图如下:
所有可能情况为:,,,,,,,,,,,.
(2)解:∵一元二次方程有实数根,
∴,
整理可得:,
∴适合的有,,共个,
所以,.
27.(1)解:∵抛物线过、两点,
∴代入抛物线解析式可得,
解得,
∴抛物线解析式为,
令可得,,解,
∵点在点右侧,
∴点坐标为,
设直线解析式为,
把、坐标代入可得,解得,
∴直线解析式为;
(2)解:∵轴,点的横坐标为,
∴,,
∵在线段上运动,
∴点在点上方,
∴,
∴当时,有最大值,的最大值为;
(3)解:由(1)(2)得点坐标为,点坐标为,
∴
∵
∴
∵轴,轴,
∴
∴
∴当是以为腰的等腰直角三角形时,,
∴点纵坐标为,
∴,解得或,
当时,则、重合,不能构成三角形,不符合题意,舍去,
∴;
(4)解:由()得,,
当以、、、为顶点的四边形是平行四边形时,则有,
当点在线段上时,由()得,
∴,此方程无实数根,
当点不在线段上时,则有,
∴,解得或,
综上可知当以、、、为顶点的四边形是平行四边形时,的值为或.
答案第1页,共2页
答案第1页,共2页
同课章节目录
