26.1.2 反比例函数的图象和性质 同步练 初中数学人教版九年级下册
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质 同步练 初中数学人教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 551.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
26.1.2 反比例函数的图象和性质 同步练
2024-2025学年初中数学人教版九年级下册
一、单选题
1.在下图中,反比例函数的图象大致是( )
A. B.
C. D.
2.已知点A(1,-3)关于x轴的对称点在反比例函数的图像上,则实数k的值为( )
A.3 B. C.-3 D.
3.已知反比例函数的图象经过点,则反比例函数图象位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
4.已知抛物线y=x2+2x﹣m﹣1与x轴没有交点,则函数y=的大致图象是( )
A. B.
C. D.
5.对于反比例函数,当时,y随x的增大而减小,则k的取值范围是( )
A. B. C. D.
6.如图,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(﹣1,﹣2) B.(﹣1,2) C.(1,﹣2) D.(﹣2,﹣1)
7.下列关于反比例函数y=-的说法正确的是( )
A.y随x的增大而增大
B.函数图象过点(2,)
C.图象位于第一、第三象限
D.x>0时,y随x的增大而增大
8.若,是函数图象上的两点,当时,下列结论正确的是
A. B. C. D.
二、填空题
9.已知点、点都在反比例函数的图象上,则k的值为 .
10.已知反比例函数的图像在每一个象限内,随的增大而增大,则的取值范围是 .
11.如图,正比例函数y=2x与反比例函数y=交于A,B两点,已知A(1,2),则点B的坐标为 .
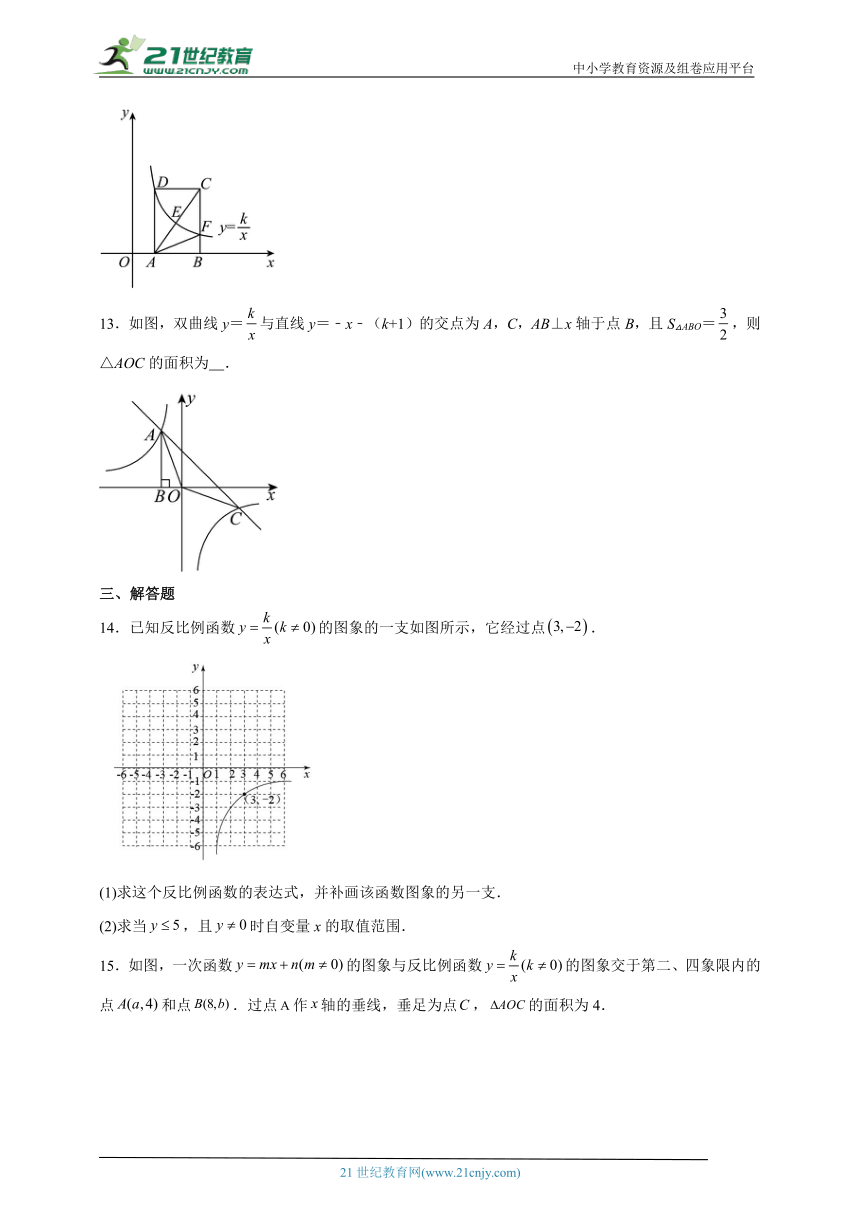
12.如图,在平面直角坐标系中,矩形的顶点,在轴的正半轴上,反比例函数的图象经过顶点,分别与对角线,边交于点,,连接,.若点为的中点,的面积为,则的值为 .
13.如图,双曲线y=与直线y=﹣x﹣(k+1)的交点为A,C,AB⊥x轴于点B,且S△ABO=,则△AOC的面积为 .
三、解答题
14.已知反比例函数的图象的一支如图所示,它经过点.
(1)求这个反比例函数的表达式,并补画该函数图象的另一支.
(2)求当,且时自变量x的取值范围.
15.如图,一次函数的图象与反比例函数的图象交于第二、四象限内的点和点.过点作轴的垂线,垂足为点,的面积为4.
(1)分别求出和的值;
(2)结合图象直接写出的解集;
(3)在轴上取点,使取得最大值时,求出点的坐标.
16.如图,一次函数y=kx+b与反比例函数y=.(其中mk≠0)图象交于A(﹣4,2),B(2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△ABO的面积;
(3)请直接写出当一次函数值大于反比例函数值时x的取值范围.
17.如图,直线OA与反比例函数()的图像交于点A(3,3),将直线OA沿y轴向下平移,与反比例函数()的图像交于点B(6,m),与y轴交于点C.
(1)求直线BC的解析式;
(2)求△ABC的面积.
参考答案:
1.D
∵k=2,可根据k>0,反比例函数图象在第一、三象限,
∴在每个象限内,y随x的增大而减小,
2.A
解:点A(1,-3)关于x轴的对称点的坐标为:(1,3),
将(1,3)代入反比例函数,
可得:k=1×3=3,
3.D
解:由题意得,,
∴函数的图象位于第二,四象限.
4.B
∵抛物线y=x2+2x﹣m﹣1与x轴没有交点,
∴△=4﹣4(﹣m﹣1)<0
∴m<﹣2
∴函数y=的图象在第二、第四象限,
5.C
当时,y随x的增大而减小,
,
.
6.A
解:∵直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点,
∴M,N两点关于原点对称,
∵点M的坐标是(1,2),
∴点N的坐标是(-1,-2).
7.D
解:A、反比例函数y= ,每个象限内,y随x的增大而增大,故此选项错误;
B、函数图象过点(2,-),故此选项错误;
C、函数图象图象位于第二、第四象限,故此选项错误;
D、x>0时,y随x的增大而增大,正确.
8.A
把点P1(x1,y1),P2(x2,y2)代入得,,则.
∵x1>x2>0,
∴,,,
即0<y1<y2.故选A.
9.
解:∵点、点都在反比例函数的图象上,
∴,
∴,
故答案为:.
10./
解:∵反比例函数的图像在每一个象限内,随的增大而增大,
∴,
∴.
故答案为:.
11.(﹣1,﹣2)
解:由于正比例函数y=2x与反比例函数y=均关于原点对称,
∴两交点A、B关于原点对称,
∵A点坐标为(1,2),
∴点B的坐标为(﹣1,﹣2).
故答案为:(﹣1,﹣2).
12.
设,根据已知条件表示出点,点坐标,易得,,由的面积为,得的面积为,所以,即可求出的值
解:设,
是矩形,且点为的中点,
点纵坐标为,
代入反比例函数解析式得,
,
点横坐标为,
点横坐标为,代入反比例函数解析式,
得,
,
,
的面积为,
的面积为,
,
,
解得.
故答案为:.
13.4
根据反比例函数k的几何意义求出k,即可得到双曲线和直线的解析式,然后联立解析式构建方程组求出A、C两点坐标,直线y=-x+2交y轴于D(0,2),根据S△AOC=S△AOD+S△OCD计算即可.
解:由题意S△ABO==,
∵k<0,∴k=﹣3,
∴双曲线为y=﹣,直线为y=﹣x+2
解得或,
∴A(﹣1,3)C(3,﹣1),
∵直线y=﹣x+2交y轴于D(0,2),
∴S△AOC=S△AOD+S△OCD=×2×1+×2×3=4,
故答案为4.
14.(1),见解析
(2)或
(1)将图中给出的点代入反比例函数表达式,即可求出解析式,并画出图象;
(2)当时,,解得,结合图象即可得出x的取值范围.
(1)解:(1)把点代入表达式,
得,
∴,
∴反比例函数的表达式是.
反比例函数图象的另一支如图所示.
(2)当时,,解得.
由图象可知,当,且时,
自变量x的取值范围是或.
15.(1),;(2)或; (3)
(1)根据题意利用三角形面积公式求得,得到,将A代入反比例函数,求出反比例函数解析式,再把B代入解析式,即可解答
(2)根据函数图象结合解析式即可判断
(3)作点关于轴的对称点,直线与轴交于,得到 ,设直线的关系式为,把将 ,代入得到解析式,即可解答
(1)∵点,
∴,
∵,即,
∴,
∵点在第二象限,
∴ ,
将代入得:,
∴反比例函数的关系式为:,
把代入得:,
∴
因此,;
(2)由图象可以看出的解集为:或;
(3)如图,作点关于轴的对称点,直线与轴交于,
此时最大,
∵
∴
设直线的关系式为,将 ,代入得:
解得:,,
∴直线的关系式为,
当时,即,解得,
∴
16.(1)y=﹣x﹣2,y=﹣;(2)6;(3)x<﹣4或0<x<2.
(1)把A点坐标分别代入一次函数和反比例函数的解析式中,即可解得k、b、m、n的值;
(2)求出一次函数y=kx+b与x轴的交点坐标,然后根据三角形的面积公式即可求出△ABO的面积;
(3)根据图象观察,当x<﹣4或0<x<2时,一次函数值大于反比例函数值.
解:(1)∵一次函数y=kx+b与反比例函数y=
(mk≠0)图象交于A(﹣4,2),B(2,n)两点.
根据反比例函数图象的对称性可知,n=﹣4,
∴,解得,
故一次函数的解析式为y=﹣x﹣2,
又知A点在反比例函数的图象上,故m=﹣8,
故反比例函数的解析式为y=﹣;
(2)如图,设一次函数的图像与y轴交于点C,
在y=﹣x﹣2中,令x=0,则y=﹣2,
∴OC=2,
∴S△AOB=×2×2+×2×4=6;
(3)根据两函数的图象可知:
当x<﹣4或0<x<2时,一次函数值大于反比例函数值.
17.(1);(2).
(1)解:∵经过点(3,3), ∴, ∴.
又∵点(6,m)在反比例函数图像上,∴m=,∴点(6, ).
设的解析式为:,,∴.
设的解析式为:,又∵经过点,∴.
∴.
(2)∵OA∥BC, ∴. 又∵, ∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
26.1.2 反比例函数的图象和性质 同步练
2024-2025学年初中数学人教版九年级下册
一、单选题
1.在下图中,反比例函数的图象大致是( )
A. B.
C. D.
2.已知点A(1,-3)关于x轴的对称点在反比例函数的图像上,则实数k的值为( )
A.3 B. C.-3 D.
3.已知反比例函数的图象经过点,则反比例函数图象位于( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
4.已知抛物线y=x2+2x﹣m﹣1与x轴没有交点,则函数y=的大致图象是( )
A. B.
C. D.
5.对于反比例函数,当时,y随x的增大而减小,则k的取值范围是( )
A. B. C. D.
6.如图,已知直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点.若点M的坐标是(1,2),则点N的坐标是( )
A.(﹣1,﹣2) B.(﹣1,2) C.(1,﹣2) D.(﹣2,﹣1)
7.下列关于反比例函数y=-的说法正确的是( )
A.y随x的增大而增大
B.函数图象过点(2,)
C.图象位于第一、第三象限
D.x>0时,y随x的增大而增大
8.若,是函数图象上的两点,当时,下列结论正确的是
A. B. C. D.
二、填空题
9.已知点、点都在反比例函数的图象上,则k的值为 .
10.已知反比例函数的图像在每一个象限内,随的增大而增大,则的取值范围是 .
11.如图,正比例函数y=2x与反比例函数y=交于A,B两点,已知A(1,2),则点B的坐标为 .
12.如图,在平面直角坐标系中,矩形的顶点,在轴的正半轴上,反比例函数的图象经过顶点,分别与对角线,边交于点,,连接,.若点为的中点,的面积为,则的值为 .
13.如图,双曲线y=与直线y=﹣x﹣(k+1)的交点为A,C,AB⊥x轴于点B,且S△ABO=,则△AOC的面积为 .
三、解答题
14.已知反比例函数的图象的一支如图所示,它经过点.
(1)求这个反比例函数的表达式,并补画该函数图象的另一支.
(2)求当,且时自变量x的取值范围.
15.如图,一次函数的图象与反比例函数的图象交于第二、四象限内的点和点.过点作轴的垂线,垂足为点,的面积为4.
(1)分别求出和的值;
(2)结合图象直接写出的解集;
(3)在轴上取点,使取得最大值时,求出点的坐标.
16.如图,一次函数y=kx+b与反比例函数y=.(其中mk≠0)图象交于A(﹣4,2),B(2,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△ABO的面积;
(3)请直接写出当一次函数值大于反比例函数值时x的取值范围.
17.如图,直线OA与反比例函数()的图像交于点A(3,3),将直线OA沿y轴向下平移,与反比例函数()的图像交于点B(6,m),与y轴交于点C.
(1)求直线BC的解析式;
(2)求△ABC的面积.
参考答案:
1.D
∵k=2,可根据k>0,反比例函数图象在第一、三象限,
∴在每个象限内,y随x的增大而减小,
2.A
解:点A(1,-3)关于x轴的对称点的坐标为:(1,3),
将(1,3)代入反比例函数,
可得:k=1×3=3,
3.D
解:由题意得,,
∴函数的图象位于第二,四象限.
4.B
∵抛物线y=x2+2x﹣m﹣1与x轴没有交点,
∴△=4﹣4(﹣m﹣1)<0
∴m<﹣2
∴函数y=的图象在第二、第四象限,
5.C
当时,y随x的增大而减小,
,
.
6.A
解:∵直线y=k1x(k1≠0)与反比例函数y=(k2≠0)的图象交于M,N两点,
∴M,N两点关于原点对称,
∵点M的坐标是(1,2),
∴点N的坐标是(-1,-2).
7.D
解:A、反比例函数y= ,每个象限内,y随x的增大而增大,故此选项错误;
B、函数图象过点(2,-),故此选项错误;
C、函数图象图象位于第二、第四象限,故此选项错误;
D、x>0时,y随x的增大而增大,正确.
8.A
把点P1(x1,y1),P2(x2,y2)代入得,,则.
∵x1>x2>0,
∴,,,
即0<y1<y2.故选A.
9.
解:∵点、点都在反比例函数的图象上,
∴,
∴,
故答案为:.
10./
解:∵反比例函数的图像在每一个象限内,随的增大而增大,
∴,
∴.
故答案为:.
11.(﹣1,﹣2)
解:由于正比例函数y=2x与反比例函数y=均关于原点对称,
∴两交点A、B关于原点对称,
∵A点坐标为(1,2),
∴点B的坐标为(﹣1,﹣2).
故答案为:(﹣1,﹣2).
12.
设,根据已知条件表示出点,点坐标,易得,,由的面积为,得的面积为,所以,即可求出的值
解:设,
是矩形,且点为的中点,
点纵坐标为,
代入反比例函数解析式得,
,
点横坐标为,
点横坐标为,代入反比例函数解析式,
得,
,
,
的面积为,
的面积为,
,
,
解得.
故答案为:.
13.4
根据反比例函数k的几何意义求出k,即可得到双曲线和直线的解析式,然后联立解析式构建方程组求出A、C两点坐标,直线y=-x+2交y轴于D(0,2),根据S△AOC=S△AOD+S△OCD计算即可.
解:由题意S△ABO==,
∵k<0,∴k=﹣3,
∴双曲线为y=﹣,直线为y=﹣x+2
解得或,
∴A(﹣1,3)C(3,﹣1),
∵直线y=﹣x+2交y轴于D(0,2),
∴S△AOC=S△AOD+S△OCD=×2×1+×2×3=4,
故答案为4.
14.(1),见解析
(2)或
(1)将图中给出的点代入反比例函数表达式,即可求出解析式,并画出图象;
(2)当时,,解得,结合图象即可得出x的取值范围.
(1)解:(1)把点代入表达式,
得,
∴,
∴反比例函数的表达式是.
反比例函数图象的另一支如图所示.
(2)当时,,解得.
由图象可知,当,且时,
自变量x的取值范围是或.
15.(1),;(2)或; (3)
(1)根据题意利用三角形面积公式求得,得到,将A代入反比例函数,求出反比例函数解析式,再把B代入解析式,即可解答
(2)根据函数图象结合解析式即可判断
(3)作点关于轴的对称点,直线与轴交于,得到 ,设直线的关系式为,把将 ,代入得到解析式,即可解答
(1)∵点,
∴,
∵,即,
∴,
∵点在第二象限,
∴ ,
将代入得:,
∴反比例函数的关系式为:,
把代入得:,
∴
因此,;
(2)由图象可以看出的解集为:或;
(3)如图,作点关于轴的对称点,直线与轴交于,
此时最大,
∵
∴
设直线的关系式为,将 ,代入得:
解得:,,
∴直线的关系式为,
当时,即,解得,
∴
16.(1)y=﹣x﹣2,y=﹣;(2)6;(3)x<﹣4或0<x<2.
(1)把A点坐标分别代入一次函数和反比例函数的解析式中,即可解得k、b、m、n的值;
(2)求出一次函数y=kx+b与x轴的交点坐标,然后根据三角形的面积公式即可求出△ABO的面积;
(3)根据图象观察,当x<﹣4或0<x<2时,一次函数值大于反比例函数值.
解:(1)∵一次函数y=kx+b与反比例函数y=
(mk≠0)图象交于A(﹣4,2),B(2,n)两点.
根据反比例函数图象的对称性可知,n=﹣4,
∴,解得,
故一次函数的解析式为y=﹣x﹣2,
又知A点在反比例函数的图象上,故m=﹣8,
故反比例函数的解析式为y=﹣;
(2)如图,设一次函数的图像与y轴交于点C,
在y=﹣x﹣2中,令x=0,则y=﹣2,
∴OC=2,
∴S△AOB=×2×2+×2×4=6;
(3)根据两函数的图象可知:
当x<﹣4或0<x<2时,一次函数值大于反比例函数值.
17.(1);(2).
(1)解:∵经过点(3,3), ∴, ∴.
又∵点(6,m)在反比例函数图像上,∴m=,∴点(6, ).
设的解析式为:,,∴.
设的解析式为:,又∵经过点,∴.
∴.
(2)∵OA∥BC, ∴. 又∵, ∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
