26.2 实际问题与反比例函数 同步练习(含答案)2024-2025学年人教版数学九年级下册
文档属性
| 名称 | 26.2 实际问题与反比例函数 同步练习(含答案)2024-2025学年人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 485.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 14:38:07 | ||
图片预览


文档简介
26.2 实际问题与反比例函数 同步练习2024-2025学年人教版数学九年级下册
一、选择题
1.李白《望天门山》诗中写道:“天门中断楚江开,碧水东流至此回.两岸青山相对出,孤帆一片日边来.”这首诗的意境可以用如图所示的函数图象进行直观描述,则y与x的函数关系式可以是( )
A. B. C. D.
2.近视眼镜的度数y(度)与镜片焦距x(米)之间有如图所示的反比例函数关系,若配制一副度数小于500度的近视眼镜,则焦距x的取值范围是( )
A. B. C. D.
3.小丽要把一篇文章录入电脑,如图是录入时间(分钟)与录字速度(字/分钟)成反比例函数的图象,该图象经过点.根据图象可知,下列说法不正确的是( )
A.这篇文章一共1500字.
B.当小丽的录字速度为75字/分钟时,录入时间为20分钟.
C.小丽在19:20开始录入,要求完成录入时不超过19:35,则小丽每分钟至少应录入90字.
D.小丽原计划每分钟录入125字,实际录入速度比原计划提高了,则小丽会比原计划提前2分钟完成任务.
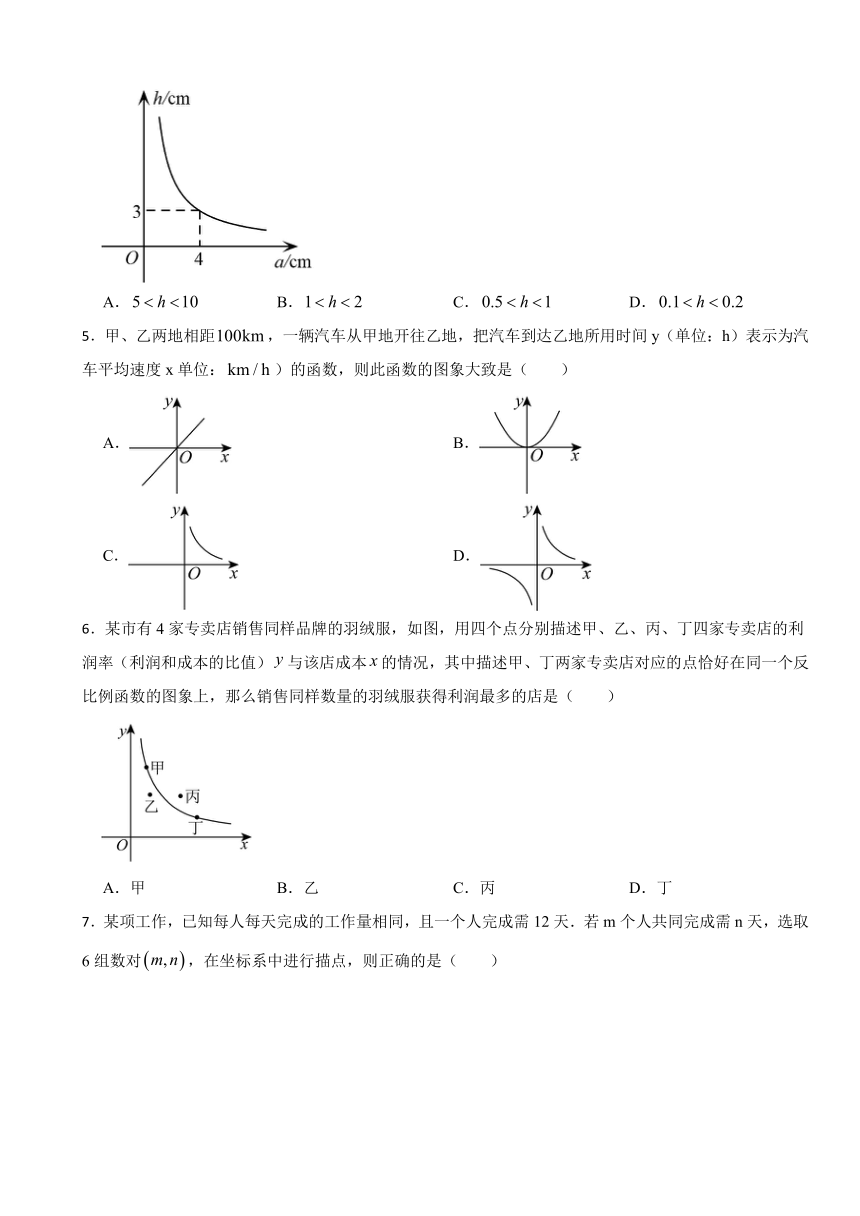
4.当三角形面积一定时,它的底边长与底边上的高成反比例函数关系,其图像如图所示,则当底边长满足时,底边上的高的取值范围是( )
A. B. C. D.
5.甲、乙两地相距,一辆汽车从甲地开往乙地,把汽车到达乙地所用时间y(单位:h)表示为汽车平均速度x单位:)的函数,则此函数的图象大致是( )
A. B.
C. D.
6.某市有4家专卖店销售同样品牌的羽绒服,如图,用四个点分别描述甲、乙、丙、丁四家专卖店的利润率(利润和成本的比值)与该店成本的情况,其中描述甲、丁两家专卖店对应的点恰好在同一个反比例函数的图象上,那么销售同样数量的羽绒服获得利润最多的店是( )
A.甲 B.乙 C.丙 D.丁
7.某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对,在坐标系中进行描点,则正确的是( )
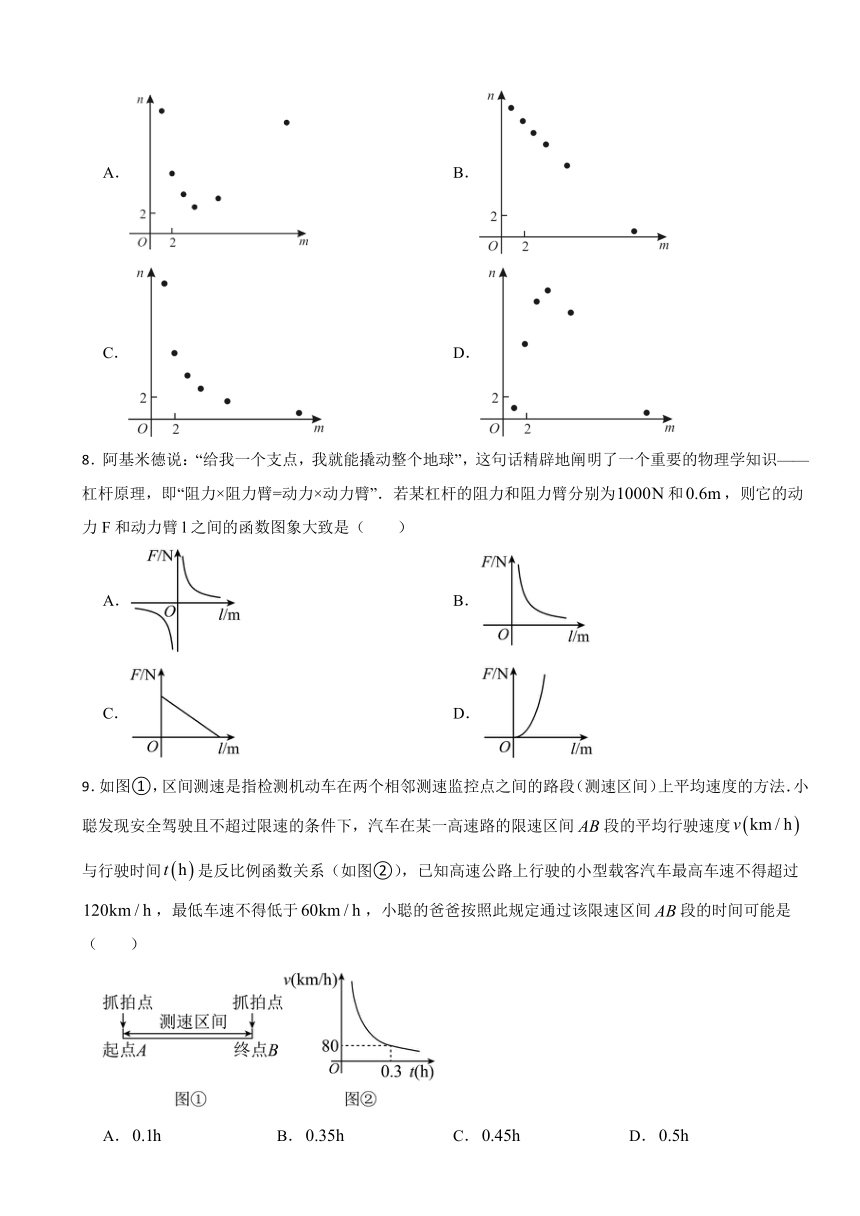
A. B.
C. D.
8.阿基米德说:“给我一个支点,我就能撬动整个地球”,这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若某杠杆的阻力和阻力臂分别为和,则它的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
9.如图①,区间测速是指检测机动车在两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小聪发现安全驾驶且不超过限速的条件下,汽车在某一高速路的限速区间段的平均行驶速度与行驶时间是反比例函数关系(如图②),已知高速公路上行驶的小型载客汽车最高车速不得超过,最低车速不得低于,小聪的爸爸按照此规定通过该限速区间段的时间可能是( )
A. B. C. D.
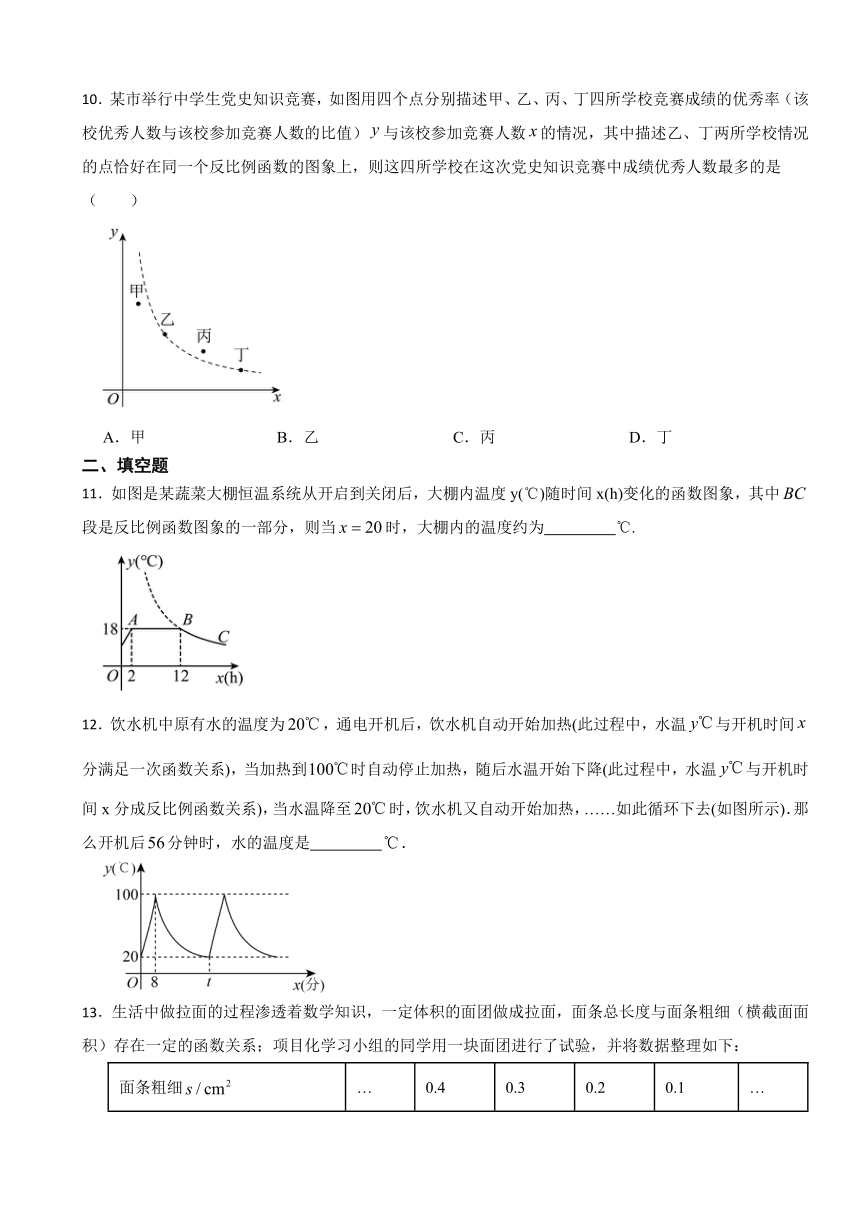
10.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题
11.如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(h)变化的函数图象,其中段是反比例函数图象的一部分,则当时,大棚内的温度约为 ℃.
12.饮水机中原有水的温度为,通电开机后,饮水机自动开始加热(此过程中,水温与开机时间分满足一次函数关系),当加热到时自动停止加热,随后水温开始下降(此过程中,水温与开机时间x分成反比例函数关系),当水温降至时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后分钟时,水的温度是 .
13.生活中做拉面的过程渗透着数学知识,一定体积的面团做成拉面,面条总长度与面条粗细(横截面面积)存在一定的函数关系;项目化学习小组的同学用一块面团进行了试验,并将数据整理如下:
面条粗细 … 0.4 0.3 0.2 0.1 …
面条总长度 … 33 44 66 132 …
根据以上数据可知,当面条总长度为220cm时,面条粗细为 .
14.区间测速是指检测机动车通过两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小禾一家在五一小长假期间出去游玩,发现汽车在安全行驶且不超速的条件下,在某一测速区间内行驶的平均速度与行驶时间之间是反比例函数关系,其函数图象如图所示.若小禾的爸爸安全行驶的平均速度为,则他们通过此测速区间的时间为 .
15.劳动教育课上,徐老师带领九(1)班同学对三类小麦种子的发芽情况进行统计(种子培养环境相同).如图,用,,三点分别表示三类种子的发芽率与该类种子用于实验的数量的情况,其中点在反比例函数图象上,则三类种子中,发芽数量最多的是 类种子.(填“A”“B”或“C”)
三、解答题
16.某超市一段时期内对某种商品经销情况进行统计分析:得到该商品的销售数量(件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价(元/件,)成反比例,销售过程中得到的部分数据如下:
售价 8 10
销售数量 70 58
(1)求与之间的函数关系式;
(2)当该商品销售数量为50件时,求每件商品的售价;
(3)设销售总额为,求的最大值.
17.如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
18.某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2) 与其深度(单位:m)是反比例函数关系,它的图象如图所示.
(1)求储存室的容积V的值;
(2)受地形条件限制,储存室的深度需要满足16≤≤25,求储存室的底面积S的取值范围.
19.王吉同学通过学习数学和物理知识,知道了根据小孔成像的科学原理,当像距(小孔到像的距离)和物体离度不变时,像离(单位:cm)是物距(小孔到物体的距离)(单位:cm)的反比例函数.当时,.
(1)求关于的函数解析式;
(2)若物体的像高为3cm,求小孔到物体的距离.
20.若以30升/分钟的速度向一个空水池内注水,40分钟可以注满水池,设注水的速度为升/分钟,注满水池需要分钟.
(1)写出与之间的函数关系式;
(2)若小明的爸爸用24分钟就将这个空水池注满水,求注水的速度.
21.试验数据显示,一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系可近似地用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图
所示).
(1)根据上述数学模型计算:
①喝酒多长时间后血液中的酒精含量达到最大值 最大值为多少
②求k的值.
(2)车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班 请说明理由.
22.为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物8 min燃毕,此时室内空气中每立方米的含药量为6 mg,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数解析式,自变量x的取值范围;药物燃烧后y关于x的函数解析式.
(2)研究表明,当空气中每立方米的含药量低于1.6 mg时员工方可进办公室,那么从消毒开始,至少经过几分钟后,员工才能回到办公室.
(3)研究表明,当空气中每立方米的含药量不低于3 mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效 为什么
23.为了节能减排,某公司从2018年开始投入技术改进资金,经技术改进后产品的成本不断降低,具体数据如表:
年度 2018 2019 2020 2021
投入技术改进资金x万元 2.5 3 4 4.5
产品成本y万元 14.4 12 9 8
(1)分析表中数据,请从一次函数和反比例函数中确定一个函数表示其变化规律,求出y与x的函数关系式,并说明理由;
(2)若2022年公司打算投入技术改进资金5万元,预计2022年产品成本比2021年降低多少万元?
(3)若2023年公司打算把投入技术改进资金x和产品成本y之和控制在12万元,请分别求出投入技术改进资金和产品成本.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】10.8
12.【答案】
13.【答案】0.06
14.【答案】
15.【答案】C
16.【答案】(1) (2)12元 (3)680元
17.【答案】(1)k=18,h=5t2;(2)x=5t+1,y=﹣5t2+18,y=,当y=13时,运动员在与正下方滑道的竖直距离是10米;(3)t=1.8,v乙>7.5
18.【答案】(1)
(2)当16≤≤25时,400≤S≤625
19.【答案】(1)解:根据题意可设,把,代入,得
,
.
(2)解:当时,.
即当物体的像高为3cm时,小孔到物体的距离为4cm.
20.【答案】(1)解:由题意得,
则,
与之间的函数关系式为;
(2)解:当时,有,
解得,
注水的速度为50升/分钟.
21.【答案】(1)解:①y=-200x2+400x
=-200(x-1)2+200,
∴喝酒1小时后血液中的酒精含量达到最大值,最大值为200毫克/百毫升.
②当x=1.5时,
二次函数y=-200x2+400x=150,
由题意,得(1.5,150)也满足反比例函数关系,
又y=(k>0),
∴k=xy=1.5×150=225.
(2)解:不能驾车去上班.理由如下:
∵晚上20:00到第二天早上7:00,共11小时,
将x=11代入y=,则y=>20,
∴第二天早上7:00不能驾车去上班.
22.【答案】(1)解:设药物燃烧时y关于x的函数解析式为y=k1x(k1>0).
将点(8,6)代入y=k1x中,得6=8k1,
∴k1=.
设药物燃烧后y关于x的函数关系式为y=(k2>0).将点(8,6)代入y=中,得6=.
∴k2=48.
∴药物燃烧时y关于x的函数解析式为y=x(0≤x≤8).药物燃烧后y关于x的函数解析式为y=(x>8).
(2)解:结合实际,令y=中y<1.6得x>30,
即从消毒开始,至少30 min后员工才能进入办公室.
(3)解:把y=3代入y=x,得x=4,
把y=3代入y=,得x=16,
∵16-4=12(min)>10 min,
∴这次消毒是有效的.
23.【答案】(1);(2)降低0.8万元;(3)投入技术改进资金为6万元,产品成本为6万元
一、选择题
1.李白《望天门山》诗中写道:“天门中断楚江开,碧水东流至此回.两岸青山相对出,孤帆一片日边来.”这首诗的意境可以用如图所示的函数图象进行直观描述,则y与x的函数关系式可以是( )
A. B. C. D.
2.近视眼镜的度数y(度)与镜片焦距x(米)之间有如图所示的反比例函数关系,若配制一副度数小于500度的近视眼镜,则焦距x的取值范围是( )
A. B. C. D.
3.小丽要把一篇文章录入电脑,如图是录入时间(分钟)与录字速度(字/分钟)成反比例函数的图象,该图象经过点.根据图象可知,下列说法不正确的是( )
A.这篇文章一共1500字.
B.当小丽的录字速度为75字/分钟时,录入时间为20分钟.
C.小丽在19:20开始录入,要求完成录入时不超过19:35,则小丽每分钟至少应录入90字.
D.小丽原计划每分钟录入125字,实际录入速度比原计划提高了,则小丽会比原计划提前2分钟完成任务.
4.当三角形面积一定时,它的底边长与底边上的高成反比例函数关系,其图像如图所示,则当底边长满足时,底边上的高的取值范围是( )
A. B. C. D.
5.甲、乙两地相距,一辆汽车从甲地开往乙地,把汽车到达乙地所用时间y(单位:h)表示为汽车平均速度x单位:)的函数,则此函数的图象大致是( )
A. B.
C. D.
6.某市有4家专卖店销售同样品牌的羽绒服,如图,用四个点分别描述甲、乙、丙、丁四家专卖店的利润率(利润和成本的比值)与该店成本的情况,其中描述甲、丁两家专卖店对应的点恰好在同一个反比例函数的图象上,那么销售同样数量的羽绒服获得利润最多的店是( )
A.甲 B.乙 C.丙 D.丁
7.某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对,在坐标系中进行描点,则正确的是( )
A. B.
C. D.
8.阿基米德说:“给我一个支点,我就能撬动整个地球”,这句话精辟地阐明了一个重要的物理学知识——杠杆原理,即“阻力×阻力臂=动力×动力臂”.若某杠杆的阻力和阻力臂分别为和,则它的动力F和动力臂l之间的函数图象大致是( )
A. B.
C. D.
9.如图①,区间测速是指检测机动车在两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小聪发现安全驾驶且不超过限速的条件下,汽车在某一高速路的限速区间段的平均行驶速度与行驶时间是反比例函数关系(如图②),已知高速公路上行驶的小型载客汽车最高车速不得超过,最低车速不得低于,小聪的爸爸按照此规定通过该限速区间段的时间可能是( )
A. B. C. D.
10.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)与该校参加竞赛人数的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
二、填空题
11.如图是某蔬菜大棚恒温系统从开启到关闭后,大棚内温度y(℃)随时间x(h)变化的函数图象,其中段是反比例函数图象的一部分,则当时,大棚内的温度约为 ℃.
12.饮水机中原有水的温度为,通电开机后,饮水机自动开始加热(此过程中,水温与开机时间分满足一次函数关系),当加热到时自动停止加热,随后水温开始下降(此过程中,水温与开机时间x分成反比例函数关系),当水温降至时,饮水机又自动开始加热,……如此循环下去(如图所示).那么开机后分钟时,水的温度是 .
13.生活中做拉面的过程渗透着数学知识,一定体积的面团做成拉面,面条总长度与面条粗细(横截面面积)存在一定的函数关系;项目化学习小组的同学用一块面团进行了试验,并将数据整理如下:
面条粗细 … 0.4 0.3 0.2 0.1 …
面条总长度 … 33 44 66 132 …
根据以上数据可知,当面条总长度为220cm时,面条粗细为 .
14.区间测速是指检测机动车通过两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小禾一家在五一小长假期间出去游玩,发现汽车在安全行驶且不超速的条件下,在某一测速区间内行驶的平均速度与行驶时间之间是反比例函数关系,其函数图象如图所示.若小禾的爸爸安全行驶的平均速度为,则他们通过此测速区间的时间为 .
15.劳动教育课上,徐老师带领九(1)班同学对三类小麦种子的发芽情况进行统计(种子培养环境相同).如图,用,,三点分别表示三类种子的发芽率与该类种子用于实验的数量的情况,其中点在反比例函数图象上,则三类种子中,发芽数量最多的是 类种子.(填“A”“B”或“C”)
三、解答题
16.某超市一段时期内对某种商品经销情况进行统计分析:得到该商品的销售数量(件)由基础销售量与浮动销售量两个部分组成,其中基本销售量保持不变,浮动销售量与售价(元/件,)成反比例,销售过程中得到的部分数据如下:
售价 8 10
销售数量 70 58
(1)求与之间的函数关系式;
(2)当该商品销售数量为50件时,求每件商品的售价;
(3)设销售总额为,求的最大值.
17.如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
18.某燃气公司计划在地下修建一个容积为V(V为定值,单位:m3)的圆柱形天然气储存室,储存室的底面积S(单位:m2) 与其深度(单位:m)是反比例函数关系,它的图象如图所示.
(1)求储存室的容积V的值;
(2)受地形条件限制,储存室的深度需要满足16≤≤25,求储存室的底面积S的取值范围.
19.王吉同学通过学习数学和物理知识,知道了根据小孔成像的科学原理,当像距(小孔到像的距离)和物体离度不变时,像离(单位:cm)是物距(小孔到物体的距离)(单位:cm)的反比例函数.当时,.
(1)求关于的函数解析式;
(2)若物体的像高为3cm,求小孔到物体的距离.
20.若以30升/分钟的速度向一个空水池内注水,40分钟可以注满水池,设注水的速度为升/分钟,注满水池需要分钟.
(1)写出与之间的函数关系式;
(2)若小明的爸爸用24分钟就将这个空水池注满水,求注水的速度.
21.试验数据显示,一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系可近似地用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图
所示).
(1)根据上述数学模型计算:
①喝酒多长时间后血液中的酒精含量达到最大值 最大值为多少
②求k的值.
(2)车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班 请说明理由.
22.为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例(如图所示),现测得药物8 min燃毕,此时室内空气中每立方米的含药量为6 mg,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数解析式,自变量x的取值范围;药物燃烧后y关于x的函数解析式.
(2)研究表明,当空气中每立方米的含药量低于1.6 mg时员工方可进办公室,那么从消毒开始,至少经过几分钟后,员工才能回到办公室.
(3)研究表明,当空气中每立方米的含药量不低于3 mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效 为什么
23.为了节能减排,某公司从2018年开始投入技术改进资金,经技术改进后产品的成本不断降低,具体数据如表:
年度 2018 2019 2020 2021
投入技术改进资金x万元 2.5 3 4 4.5
产品成本y万元 14.4 12 9 8
(1)分析表中数据,请从一次函数和反比例函数中确定一个函数表示其变化规律,求出y与x的函数关系式,并说明理由;
(2)若2022年公司打算投入技术改进资金5万元,预计2022年产品成本比2021年降低多少万元?
(3)若2023年公司打算把投入技术改进资金x和产品成本y之和控制在12万元,请分别求出投入技术改进资金和产品成本.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】10.8
12.【答案】
13.【答案】0.06
14.【答案】
15.【答案】C
16.【答案】(1) (2)12元 (3)680元
17.【答案】(1)k=18,h=5t2;(2)x=5t+1,y=﹣5t2+18,y=,当y=13时,运动员在与正下方滑道的竖直距离是10米;(3)t=1.8,v乙>7.5
18.【答案】(1)
(2)当16≤≤25时,400≤S≤625
19.【答案】(1)解:根据题意可设,把,代入,得
,
.
(2)解:当时,.
即当物体的像高为3cm时,小孔到物体的距离为4cm.
20.【答案】(1)解:由题意得,
则,
与之间的函数关系式为;
(2)解:当时,有,
解得,
注水的速度为50升/分钟.
21.【答案】(1)解:①y=-200x2+400x
=-200(x-1)2+200,
∴喝酒1小时后血液中的酒精含量达到最大值,最大值为200毫克/百毫升.
②当x=1.5时,
二次函数y=-200x2+400x=150,
由题意,得(1.5,150)也满足反比例函数关系,
又y=(k>0),
∴k=xy=1.5×150=225.
(2)解:不能驾车去上班.理由如下:
∵晚上20:00到第二天早上7:00,共11小时,
将x=11代入y=,则y=>20,
∴第二天早上7:00不能驾车去上班.
22.【答案】(1)解:设药物燃烧时y关于x的函数解析式为y=k1x(k1>0).
将点(8,6)代入y=k1x中,得6=8k1,
∴k1=.
设药物燃烧后y关于x的函数关系式为y=(k2>0).将点(8,6)代入y=中,得6=.
∴k2=48.
∴药物燃烧时y关于x的函数解析式为y=x(0≤x≤8).药物燃烧后y关于x的函数解析式为y=(x>8).
(2)解:结合实际,令y=中y<1.6得x>30,
即从消毒开始,至少30 min后员工才能进入办公室.
(3)解:把y=3代入y=x,得x=4,
把y=3代入y=,得x=16,
∵16-4=12(min)>10 min,
∴这次消毒是有效的.
23.【答案】(1);(2)降低0.8万元;(3)投入技术改进资金为6万元,产品成本为6万元
