北师大版数学九年级下3.3垂径定理课件(共21张ppt)
文档属性
| 名称 | 北师大版数学九年级下3.3垂径定理课件(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-06 00:00:00 | ||
图片预览





文档简介
课件21张PPT。3.3 垂径定理阳山县青莲中学数学组九年级数学(下)第三章 圆1.圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.2.圆也是中心对称图形.它的对称中心就是圆心.知识回顾4.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等。 5.定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
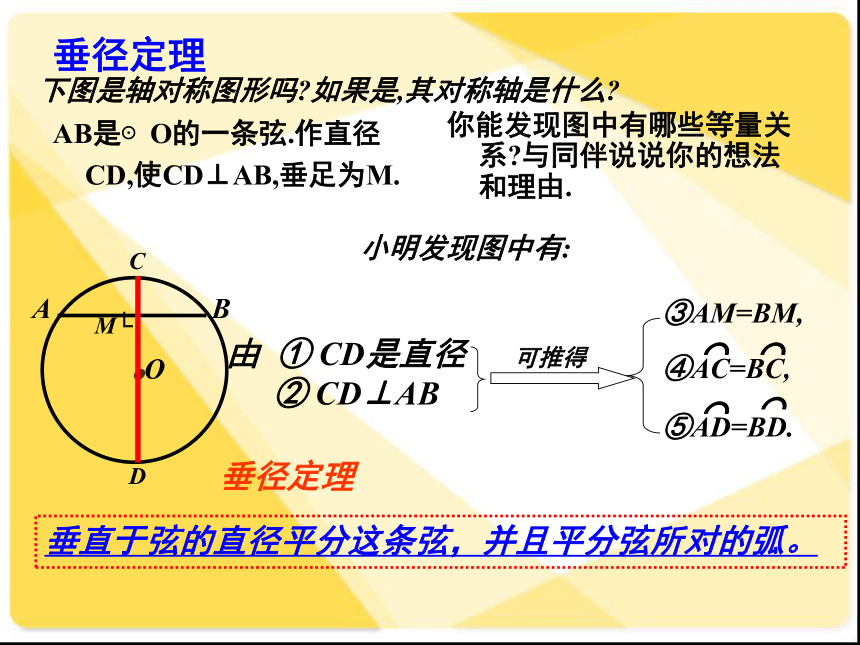
3.顶点在圆心的角叫做圆心角.③AM=BM,垂径定理AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.
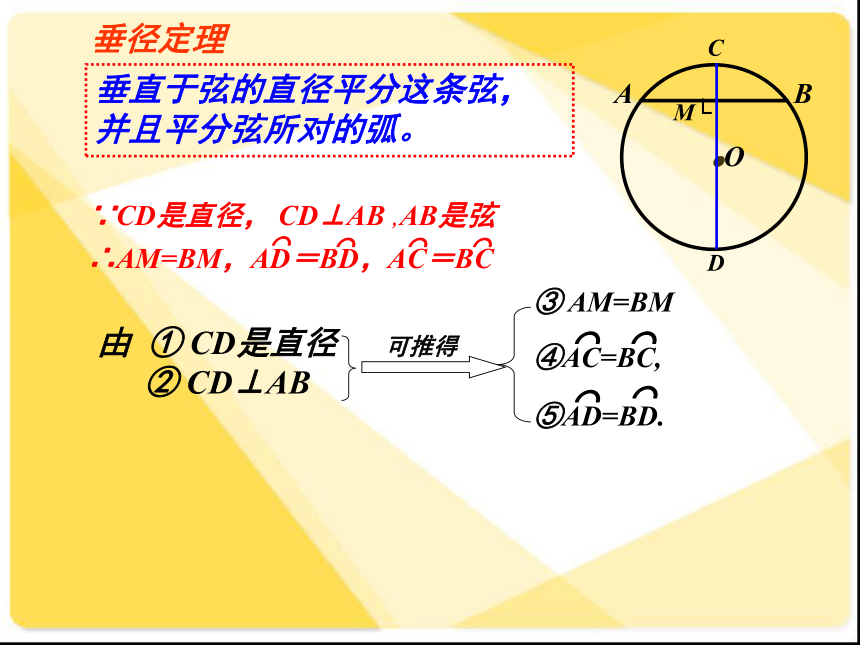
你能发现图中有哪些等量关系?与同伴说说你的想法和理由.下图是轴对称图形吗?如果是,其对称轴是什么?小明发现图中有: 由 ① CD是直径② CD⊥AB垂直于弦的直径平分这条弦,并且平分弦所对的弧。垂径定理证明:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM∴Rt△OAM≌Rt△OBM∴AM=BM, ∠AOC=∠BOC∵∠AOD=180°-∠AOC, ∠BOD=180°-∠BOC∴ ∠AOD=∠BOD垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧③ AM=BM 由 ① CD是直径② CD⊥AB垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的弧。∵CD是直径, CD⊥AB ,AB是弦∴AM=BM,AD=BD,AC=BC⌒⌒⌒⌒②CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AM=BM. 你能发现图中有哪些等量关系?与同伴说说
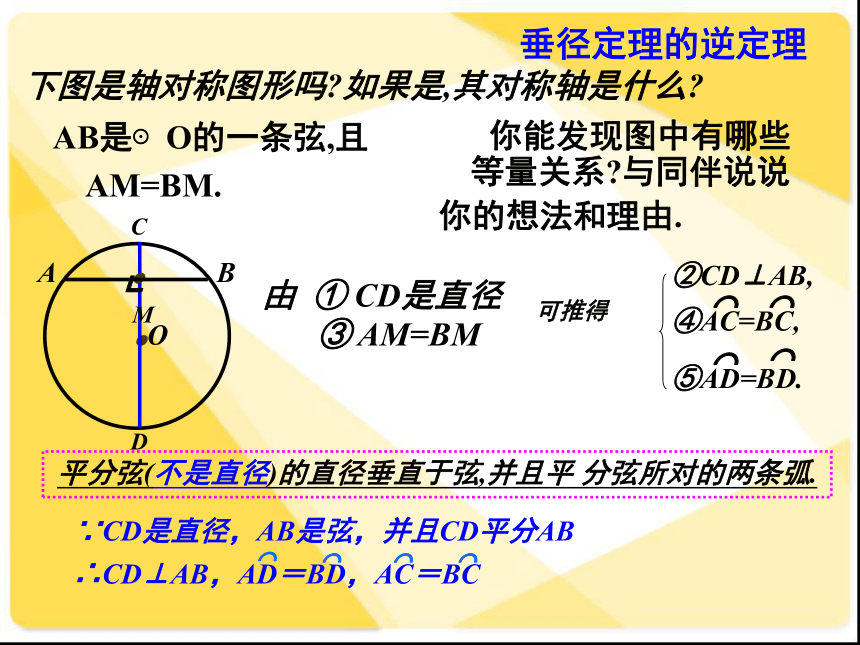
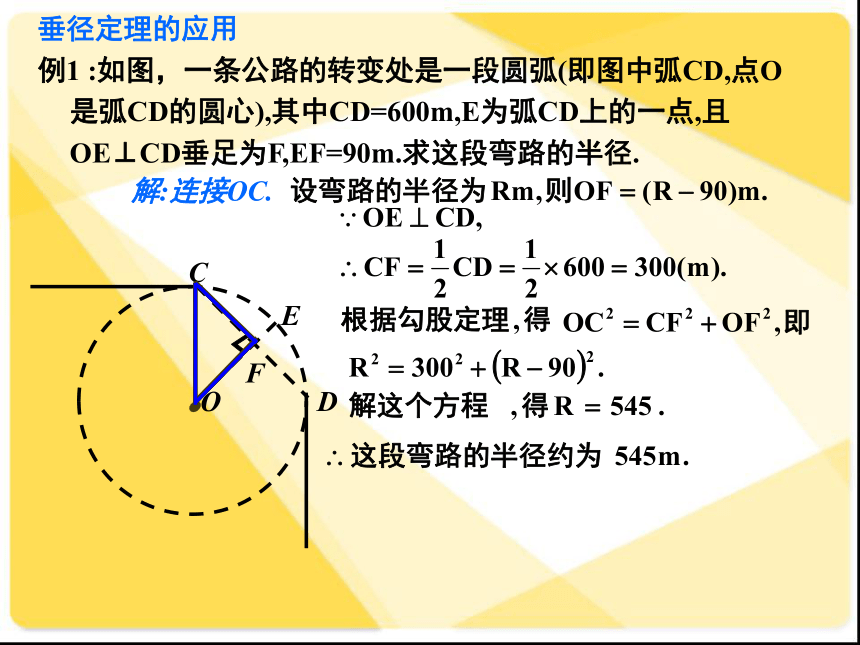
你的想法和理由.下图是轴对称图形吗?如果是,其对称轴是什么? 由 ① CD是直径③ AM=BM┗平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.∵CD是直径,AB是弦,并且CD平分AB∴CD⊥AB,AD=BD,AC=BC⌒⌒⌒⌒垂径定理的应用例1 :如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.讨论(1)过圆心 (2)垂直于弦 (3)平分弦 (4)平分弦所对优弧 (5)平分弦所对的劣弧(3)
(1)(2)
(4)
(5)(2)
(3)(1)
(4)
(5)(1)
(4)(3)
(2)
(5)(1)
(5)(3)
(4)
(2)(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧
(3)平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧命题(1):平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧∵CD是直径,AB是弦,并且CD平分AB∴CD⊥AB,AD=BD,AC=BC⌒⌒⌒⌒命题(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧∵ AB是弦,CD平分AB,CD ⊥AB,
∴ CD是直径, AD=BD,AC=BC命题(3):平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧∵ CD是直径,AB是弦,并且AD=BD (AC=BC)
∴ CD平分AB,AC=BC(AD=BD)CD ⊥AB 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。推论(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对 的两条弧(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧(3)平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧垂径定理记忆弧的中点到弦的距离,叫弓形高或弓高,如图线段CM是弓高圆心到弦的距离,叫弦心距。如图线段OM是O到弦AB的弦心距。赵州石拱桥1. 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).随堂练习1赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.随堂练习1如果圆的两条弦平行,那么这两条弦所夹的弧相等吗?为什么?EF└└MN随堂练习2还有其他情况吗?如图,已知⊙O的半径为30mm,弦AB=36mm.则点O到AB的距离及 ∠OAB的余弦值。知识技能2C 如图,两个圆都是以O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上,你认为AC与BD的大小有什么关系?为什么?
理由:过O作OE⊥AB于E,解后指出:在圆中,解有关弦的问题时,常常需要作出“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作弦的垂线段。则 AE=BE,CE=DE∴AE-CE=BE-DE即AC=BD数学理解3解:AC=BDO如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.数学理解4AB判断(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)圆的不与直径垂直的弦必不被这条直径平分………………………………………...( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )(5)圆内两条非直径的弦不能互相平分( )×√××√挑战自我(6)平分弦的直径,平分这条弦所对的弧 ( ) (7)平分弦的直线,必定过圆心 ( )(8)一条直线平分弦(这条弦不是直径),那么这条直线垂直这条弦 ( )???(9)弦的垂直平分线一定是圆的直径 ( )(10)平分弧的直线,平分这条弧所对的 弦( )(11)弦垂直于直径,这条直径就被弦平分 ( )???这节课有何收获?!你
3.顶点在圆心的角叫做圆心角.③AM=BM,垂径定理AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.
你能发现图中有哪些等量关系?与同伴说说你的想法和理由.下图是轴对称图形吗?如果是,其对称轴是什么?小明发现图中有: 由 ① CD是直径② CD⊥AB垂直于弦的直径平分这条弦,并且平分弦所对的弧。垂径定理证明:连接OA,OB,则OA=OB.在Rt△OAM和Rt△OBM中,∵OA=OB,OM=OM∴Rt△OAM≌Rt△OBM∴AM=BM, ∠AOC=∠BOC∵∠AOD=180°-∠AOC, ∠BOD=180°-∠BOC∴ ∠AOD=∠BOD垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧③ AM=BM 由 ① CD是直径② CD⊥AB垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的弧。∵CD是直径, CD⊥AB ,AB是弦∴AM=BM,AD=BD,AC=BC⌒⌒⌒⌒②CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AM=BM. 你能发现图中有哪些等量关系?与同伴说说
你的想法和理由.下图是轴对称图形吗?如果是,其对称轴是什么? 由 ① CD是直径③ AM=BM┗平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.∵CD是直径,AB是弦,并且CD平分AB∴CD⊥AB,AD=BD,AC=BC⌒⌒⌒⌒垂径定理的应用例1 :如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.讨论(1)过圆心 (2)垂直于弦 (3)平分弦 (4)平分弦所对优弧 (5)平分弦所对的劣弧(3)
(1)(2)
(4)
(5)(2)
(3)(1)
(4)
(5)(1)
(4)(3)
(2)
(5)(1)
(5)(3)
(4)
(2)(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧
(3)平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧命题(1):平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧∵CD是直径,AB是弦,并且CD平分AB∴CD⊥AB,AD=BD,AC=BC⌒⌒⌒⌒命题(2):弦的垂直平分线经过圆心,并且平分弦所对的两条弧∵ AB是弦,CD平分AB,CD ⊥AB,
∴ CD是直径, AD=BD,AC=BC命题(3):平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧∵ CD是直径,AB是弦,并且AD=BD (AC=BC)
∴ CD平分AB,AC=BC(AD=BD)CD ⊥AB 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。推论(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对 的两条弧(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧(3)平分一条弧的直径,垂直平分弧所对的弦,并且平分弦所对的另一条弧垂径定理记忆弧的中点到弦的距离,叫弓形高或弓高,如图线段CM是弓高圆心到弦的距离,叫弦心距。如图线段OM是O到弦AB的弦心距。赵州石拱桥1. 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).随堂练习1赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.随堂练习1如果圆的两条弦平行,那么这两条弦所夹的弧相等吗?为什么?EF└└MN随堂练习2还有其他情况吗?如图,已知⊙O的半径为30mm,弦AB=36mm.则点O到AB的距离及 ∠OAB的余弦值。知识技能2C 如图,两个圆都是以O为圆心,小圆的弦CD与大圆的弦AB在同一条直线上,你认为AC与BD的大小有什么关系?为什么?
理由:过O作OE⊥AB于E,解后指出:在圆中,解有关弦的问题时,常常需要作出“垂直于弦的直径”作为辅助线,实际上,往往只需从圆心作弦的垂线段。则 AE=BE,CE=DE∴AE-CE=BE-DE即AC=BD数学理解3解:AC=BDO如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.数学理解4AB判断(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………………………………..( )(2)弦所对的两弧中点的连线,垂直于弦,并且经过圆心……………………………………..( )(3)圆的不与直径垂直的弦必不被这条直径平分………………………………………...( )(4)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………………………………( )(5)圆内两条非直径的弦不能互相平分( )×√××√挑战自我(6)平分弦的直径,平分这条弦所对的弧 ( ) (7)平分弦的直线,必定过圆心 ( )(8)一条直线平分弦(这条弦不是直径),那么这条直线垂直这条弦 ( )???(9)弦的垂直平分线一定是圆的直径 ( )(10)平分弧的直线,平分这条弧所对的 弦( )(11)弦垂直于直径,这条直径就被弦平分 ( )???这节课有何收获?!你
