2024-2025学年陕西省西安市西咸新区九年级(上)第三次月考数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年陕西省西安市西咸新区九年级(上)第三次月考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 465.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-16 00:00:00 | ||
图片预览




文档简介
2024-2025学年陕西省西安市西咸新区九年级(上)第三次月考
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列光源的光线所形成的投影不能称为中心投影的是( )
A. 探照灯 B. 台灯 C. 路灯 D. 月亮
2.下列关系式中,是的反比例函数的是( )
A. B. C. D.
3.“斗”和“升”是古时人们盛粮食和计量粮食的工具,如图是“斗”的图片,则它的俯视图是( )
A. B. C. D.
4.菱形、正方形一定具有而矩形不一定具有的性质是( )
A. 对边相等 B. 对边平行 C. 对角线互相平分 D. 对角线互相垂直
5.关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. C. 且 D. 且
6.如图,在直角坐标系中,与是位似图形,已知点,则位似中心的坐标是( )
A.
B.
C.
D.
7.近年来我国航天事业取得了一系列的伟大成就,现有张正面印有航天飞行任务标识的卡片,它们除标识之外其他完全相同,把这张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
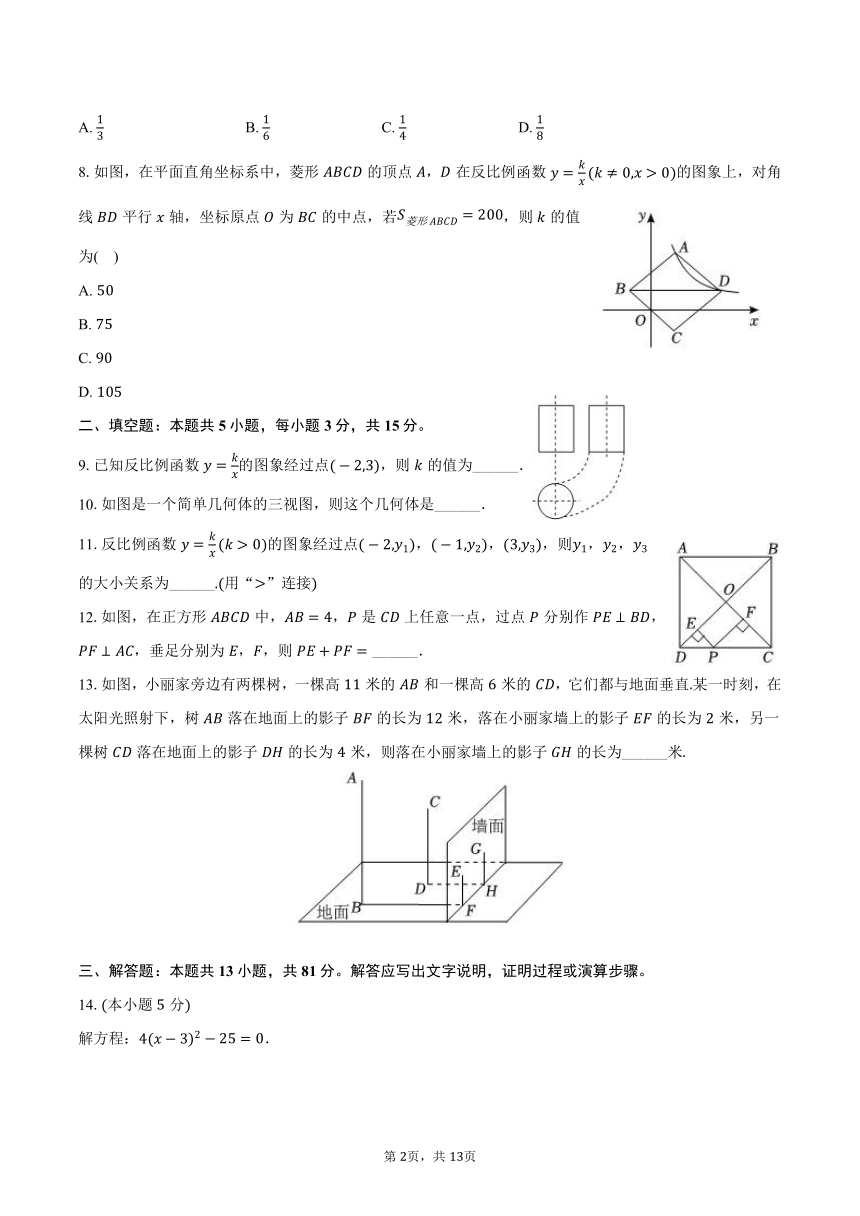
8.如图,在平面直角坐标系中,菱形的顶点,在反比例函数的图象上,对角线平行轴,坐标原点为的中点,若,则的值为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
9.已知反比例函数的图象经过点,则的值为______.
10.如图是一个简单几何体的三视图,则这个几何体是______.
11.反比例函数的图象经过点,,,则,,的大小关系为______用“”连接
12.如图,在正方形中,,是上任意一点,过点分别作,,垂足分别为,,则 ______.
13.如图,小丽家旁边有两棵树,一棵高米的和一棵高米的,它们都与地面垂直某一时刻,在太阳光照射下,树落在地面上的影子的长为米,落在小丽家墙上的影子的长为米,另一棵树落在地面上的影子的长为米,则落在小丽家墙上的影子的长为______米
三、解答题:本题共13小题,共81分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
解方程:.
15.本小题分
已知反比例函数的图象,当时,随的增大而增大,求的取值范围.
16.本小题分
如图,在平面直角坐标系中,和是以坐标原点为位似中心的位似图形,且点的坐标为,点的坐标为若点的坐标为,求点的坐标.
17.本小题分
如图,在中,,是的中点,过点作,使,连接求证:四边形是矩形.
18.本小题分
如图,已知,请用尺规作图法,以点为位似中心作,使得∽,且点在边上,点在边上,相似比为:保留作图痕迹,不写作法
19.本小题分
如图,在中,,是上一点,,.
求证:∽;
若,,的面积为,求的面积.
20.本小题分
为进一步规范办学行为,促进教育公平,某校起始年级实行“阳光分班”,采用电脑随机分班,分班时对所有学生一视同仁小林和小新两位同学被录取到该校读七年级,这所学校七年级有班、班、班、班共四个班.
小林分到班的概率是______;
请用列表或画树状图的方法求小林和小新两位同学分到同一个班的概率.
21.本小题分
已知反比例函数与一次函数的图象交于点和点.
求反比例函数的表达式;
当时,求的取值范围.
22.本小题分
如图,在菱形中,点在边上不与点,重合,射线与射线交于点.
若,,则 ______;
求证:.
23.本小题分
如图,区间测速是指检测机动车在两个相邻测速监控点之间的路段测速区间上的平均速度小颖发现安全驾驶且不超过限速的条件下,汽车在某一高速路的限速区间段的平均行驶速度单位:与行驶时间单位:是反比例函数关系如图.
求与的函数表达式;
已知在限速区间上行驶的小型载客汽车的最高车速不得超过,最低车速不得低于,求小颖的爸爸按照此规定通过该限速区间段的时间范围.
24.本小题分
某县进行街道改造用移动围栏围一个矩形安全区域,两面靠墙位置的墙最大可用长度为米,位置的墙最大可用长度为米,另两边用移动围栏围成,中间也用移动围栏隔开,分成两个安全场地及一处通道,并在如图所示的三处各留米宽的门虚线部分围成后移动围栏总共用了米.
若移动围栏围成的矩形的一边长为米,则另一边为______米;
若移动围栏围成的矩形的面积为平方米,求边的长.
25.本小题分
数学思考
我国古代经典数学著作孙子算经有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”其大意如下:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆如图,它的影长五寸备注:丈尺,尺寸,问竹竿长多少?若设竹竿长尺,则可列方程:______.
解决问题
数学兴趣小组的同学对某古塔进行了测量,测量方法如下:如图,甲同学在古塔的影子顶端处竖直立一根木棒,并测得此时木棒的影长,然后,乙同学在的延长线上找出一点,使得,,三点在同一直线上,并测得已知图中所有点均在同一平面内,木棒,,,请根据以上测量数据,求古塔的高度.
26.本小题分
综合实践课上,老师带领同学们研究反比例函数图象平移的性质,已知反比例函数的图象,老师先将的图象向左平移个单位长度,再将函数的图象向下平移个单位长度,可以得到新函数的图象如图,老师已经画出了新函数图象的一支曲线.
请在图中画出新函数图象的另一支曲线,并写出这个新函数的一条性质;
若过点作一直线,与这个新函数图象仅有一个交点,求该交点的横坐标;
直线与这个新函数图象在第一象限交于点,在第三象限交于点,为线段的中点,过点的一条直线与这个新函数的图象交于,两点点在第三象限,若以,,,为顶点组成的四边形的面积为,请直接写出点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.圆柱
11.
12.
13.
14.解:
,.
15.解:反比例函数的图象,当时,随的增大而增大,
,
解得.
16.解:和是以坐标原点为位似中心的位似图形,点的坐标为,点的坐标为,
∽,且相似比为:,
点的坐标为,
点的坐标.
17.证明:,,
四边形是平行四边形,
,是的中点,
,
,
四边形是矩形.
18.解:如下图:即为所求.
19.证明:,
,
,,
,
≌;
解:由可得≌,
,
,
,
解得:.
20.(1)
( 2 ) 画树状图为:
21.解:一次函数的图象经过点和点.
,,
,.
反比例函数图象过点,
,
反比例函数解析式为;
由函数图象可知,当时,的取值范围为或.
22.
23.解:由题意可设,
将代入得,,
;
答:与的函数表达式为;
当时,,
当时,,
小颖的爸爸按照此规定通过该限速区间段的时间范围为.
24.
25.
26.解:当时,,当时,,当时,,
根据上述个点描点连线绘制函数图象如下:
从函数图象看,函数是中心对称图形,对称中心为答案不唯一;
设过点的一直线为,
联立上式和原函数的表达式并整理得:,
则,
解得:,
则方程为:,
解得:,
即该交点的横坐标为;
联立和曲线的表达式得:,
解得:或,
即点、的坐标分别为:、,
则点,
曲线为以点为对称中心的对称图形,
则,而,
则四边形为平行四边形,
则,
设直线过点的表达式为:,
联立上式和曲线的表达式得:,
解得:,,
则,
过点作轴交于点,则点,
则,
则,
解得:舍去或,
而,
则点.
第1页,共1页
数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列光源的光线所形成的投影不能称为中心投影的是( )
A. 探照灯 B. 台灯 C. 路灯 D. 月亮
2.下列关系式中,是的反比例函数的是( )
A. B. C. D.
3.“斗”和“升”是古时人们盛粮食和计量粮食的工具,如图是“斗”的图片,则它的俯视图是( )
A. B. C. D.
4.菱形、正方形一定具有而矩形不一定具有的性质是( )
A. 对边相等 B. 对边平行 C. 对角线互相平分 D. 对角线互相垂直
5.关于的一元二次方程有两个不相等的实数根,则的取值范围是( )
A. B. C. 且 D. 且
6.如图,在直角坐标系中,与是位似图形,已知点,则位似中心的坐标是( )
A.
B.
C.
D.
7.近年来我国航天事业取得了一系列的伟大成就,现有张正面印有航天飞行任务标识的卡片,它们除标识之外其他完全相同,把这张卡片背面朝上洗匀,从中随机抽取一张,放回洗匀后,再从中随机抽取一张,两次抽取的卡片正面相同的概率为( )
A. B. C. D.
8.如图,在平面直角坐标系中,菱形的顶点,在反比例函数的图象上,对角线平行轴,坐标原点为的中点,若,则的值为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
9.已知反比例函数的图象经过点,则的值为______.
10.如图是一个简单几何体的三视图,则这个几何体是______.
11.反比例函数的图象经过点,,,则,,的大小关系为______用“”连接
12.如图,在正方形中,,是上任意一点,过点分别作,,垂足分别为,,则 ______.
13.如图,小丽家旁边有两棵树,一棵高米的和一棵高米的,它们都与地面垂直某一时刻,在太阳光照射下,树落在地面上的影子的长为米,落在小丽家墙上的影子的长为米,另一棵树落在地面上的影子的长为米,则落在小丽家墙上的影子的长为______米
三、解答题:本题共13小题,共81分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
解方程:.
15.本小题分
已知反比例函数的图象,当时,随的增大而增大,求的取值范围.
16.本小题分
如图,在平面直角坐标系中,和是以坐标原点为位似中心的位似图形,且点的坐标为,点的坐标为若点的坐标为,求点的坐标.
17.本小题分
如图,在中,,是的中点,过点作,使,连接求证:四边形是矩形.
18.本小题分
如图,已知,请用尺规作图法,以点为位似中心作,使得∽,且点在边上,点在边上,相似比为:保留作图痕迹,不写作法
19.本小题分
如图,在中,,是上一点,,.
求证:∽;
若,,的面积为,求的面积.
20.本小题分
为进一步规范办学行为,促进教育公平,某校起始年级实行“阳光分班”,采用电脑随机分班,分班时对所有学生一视同仁小林和小新两位同学被录取到该校读七年级,这所学校七年级有班、班、班、班共四个班.
小林分到班的概率是______;
请用列表或画树状图的方法求小林和小新两位同学分到同一个班的概率.
21.本小题分
已知反比例函数与一次函数的图象交于点和点.
求反比例函数的表达式;
当时,求的取值范围.
22.本小题分
如图,在菱形中,点在边上不与点,重合,射线与射线交于点.
若,,则 ______;
求证:.
23.本小题分
如图,区间测速是指检测机动车在两个相邻测速监控点之间的路段测速区间上的平均速度小颖发现安全驾驶且不超过限速的条件下,汽车在某一高速路的限速区间段的平均行驶速度单位:与行驶时间单位:是反比例函数关系如图.
求与的函数表达式;
已知在限速区间上行驶的小型载客汽车的最高车速不得超过,最低车速不得低于,求小颖的爸爸按照此规定通过该限速区间段的时间范围.
24.本小题分
某县进行街道改造用移动围栏围一个矩形安全区域,两面靠墙位置的墙最大可用长度为米,位置的墙最大可用长度为米,另两边用移动围栏围成,中间也用移动围栏隔开,分成两个安全场地及一处通道,并在如图所示的三处各留米宽的门虚线部分围成后移动围栏总共用了米.
若移动围栏围成的矩形的一边长为米,则另一边为______米;
若移动围栏围成的矩形的面积为平方米,求边的长.
25.本小题分
数学思考
我国古代经典数学著作孙子算经有首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”其大意如下:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆如图,它的影长五寸备注:丈尺,尺寸,问竹竿长多少?若设竹竿长尺,则可列方程:______.
解决问题
数学兴趣小组的同学对某古塔进行了测量,测量方法如下:如图,甲同学在古塔的影子顶端处竖直立一根木棒,并测得此时木棒的影长,然后,乙同学在的延长线上找出一点,使得,,三点在同一直线上,并测得已知图中所有点均在同一平面内,木棒,,,请根据以上测量数据,求古塔的高度.
26.本小题分
综合实践课上,老师带领同学们研究反比例函数图象平移的性质,已知反比例函数的图象,老师先将的图象向左平移个单位长度,再将函数的图象向下平移个单位长度,可以得到新函数的图象如图,老师已经画出了新函数图象的一支曲线.
请在图中画出新函数图象的另一支曲线,并写出这个新函数的一条性质;
若过点作一直线,与这个新函数图象仅有一个交点,求该交点的横坐标;
直线与这个新函数图象在第一象限交于点,在第三象限交于点,为线段的中点,过点的一条直线与这个新函数的图象交于,两点点在第三象限,若以,,,为顶点组成的四边形的面积为,请直接写出点的坐标.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.圆柱
11.
12.
13.
14.解:
,.
15.解:反比例函数的图象,当时,随的增大而增大,
,
解得.
16.解:和是以坐标原点为位似中心的位似图形,点的坐标为,点的坐标为,
∽,且相似比为:,
点的坐标为,
点的坐标.
17.证明:,,
四边形是平行四边形,
,是的中点,
,
,
四边形是矩形.
18.解:如下图:即为所求.
19.证明:,
,
,,
,
≌;
解:由可得≌,
,
,
,
解得:.
20.(1)
( 2 ) 画树状图为:
21.解:一次函数的图象经过点和点.
,,
,.
反比例函数图象过点,
,
反比例函数解析式为;
由函数图象可知,当时,的取值范围为或.
22.
23.解:由题意可设,
将代入得,,
;
答:与的函数表达式为;
当时,,
当时,,
小颖的爸爸按照此规定通过该限速区间段的时间范围为.
24.
25.
26.解:当时,,当时,,当时,,
根据上述个点描点连线绘制函数图象如下:
从函数图象看,函数是中心对称图形,对称中心为答案不唯一;
设过点的一直线为,
联立上式和原函数的表达式并整理得:,
则,
解得:,
则方程为:,
解得:,
即该交点的横坐标为;
联立和曲线的表达式得:,
解得:或,
即点、的坐标分别为:、,
则点,
曲线为以点为对称中心的对称图形,
则,而,
则四边形为平行四边形,
则,
设直线过点的表达式为:,
联立上式和曲线的表达式得:,
解得:,,
则,
过点作轴交于点,则点,
则,
则,
解得:舍去或,
而,
则点.
第1页,共1页
同课章节目录
