3.4 第2课时 圆周角定理的推论2,3课件(共33张PPT) 2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 3.4 第2课时 圆周角定理的推论2,3课件(共33张PPT) 2024-2025学年北师大版九年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 20:22:07 | ||
图片预览





文档简介
(共33张PPT)
北师版·九年级下册
第2课时 圆周角定理的推论2,3
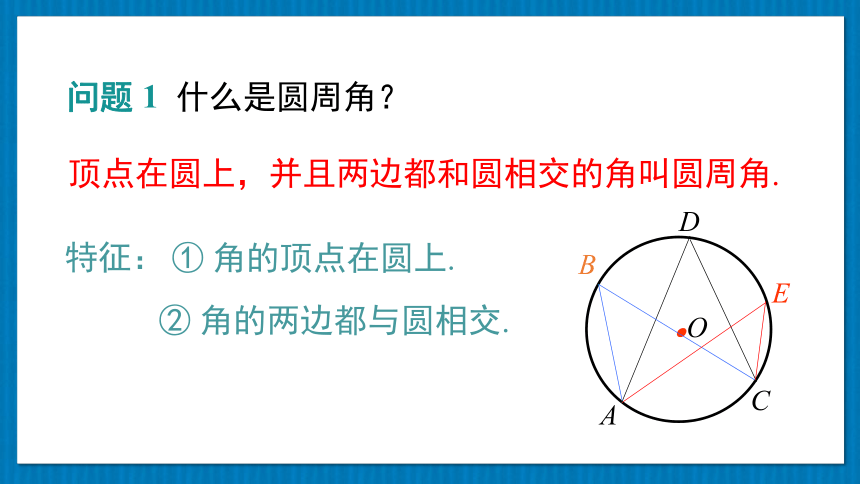
问题 1 什么是圆周角?
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
●O
B
A
C
D
E
问题 2 什么是圆周角定理?
圆上一条弧所对的圆周角等于它所对的圆心角的 .
即 ∠ABC = ∠AOC.
一半
C
A
B
O
C
A
B
O
C
A
B
O
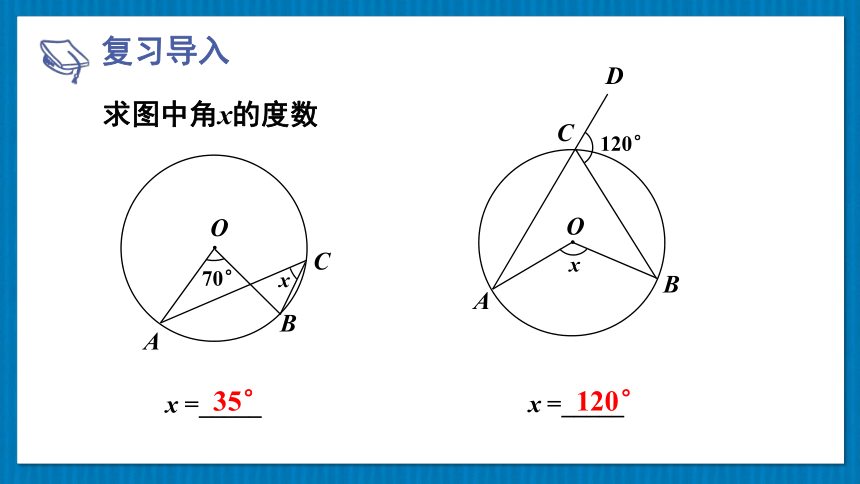
复习导入
求图中角x的度数
·
A
O
B
70°
x
x =_____
C
·
O
A
B
C
D
120°
x
x =_____
35°
120°
圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
复习导入
求图中角x的度数
复习导入
求图中角x的度数
·
A
O
B
60°
x
x =_____
C
·
O
A
B
C
D
20°
x
x =_____
D
60°
E
F
30°
50°
复习导入
求图中角x的度数
推论 同弧或等弧所对的圆周角相等.
探究新知
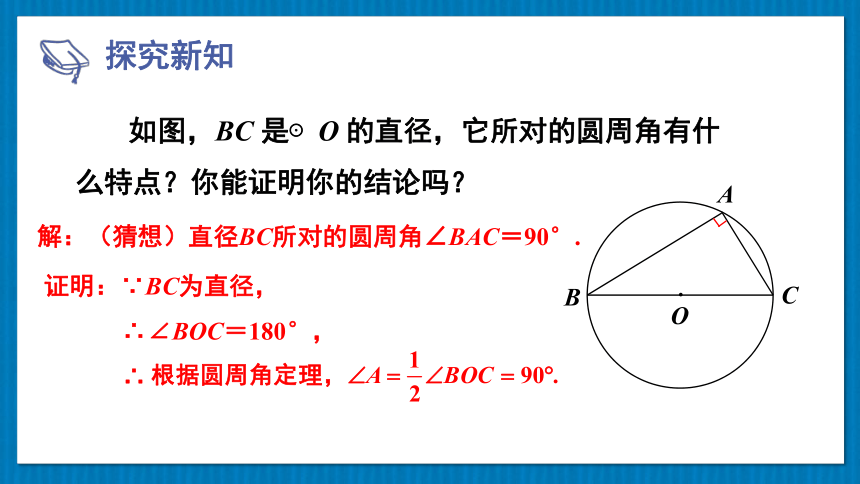
如图,BC 是⊙O 的直径,它所对的圆周角有什么特点?你能证明你的结论吗?
·
O
A
B
C
解:(猜想)直径BC所对的圆周角∠BAC=90°.
证明:∵BC为直径,
∴∠BOC=180°,
∴
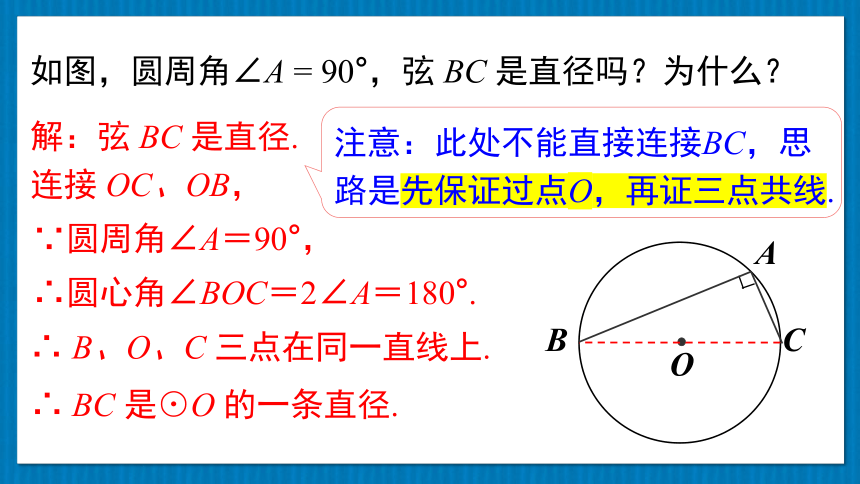
如图,圆周角∠A = 90°,弦 BC 是直径吗?为什么?
解:弦 BC 是直径.
连接 OC、OB,
注意:此处不能直接连接BC,思路是先保证过点O,再证三点共线.
∴ BC 是⊙O 的一条直径.
∴ B、O、C 三点在同一直线上.
∴圆心角∠BOC=2∠A=180°.
∵圆周角∠A=90°,
A
B
O
C
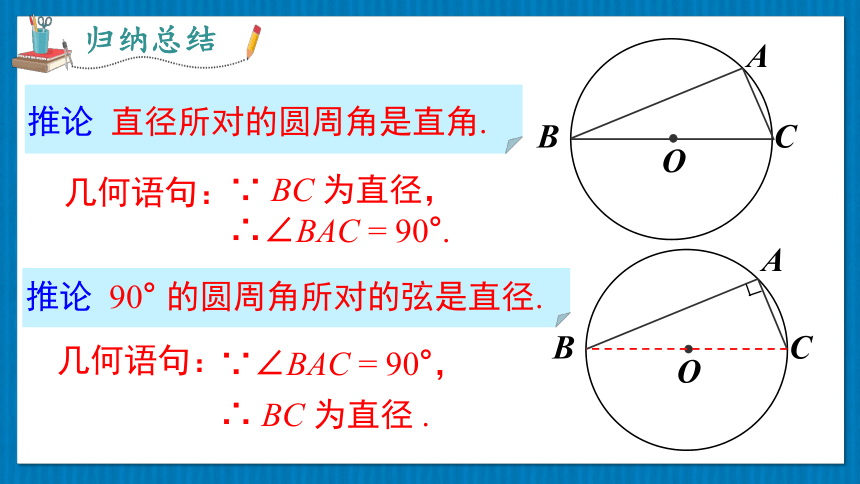
归纳总结
∵ BC 为直径,
∴∠BAC = 90°.
几何语句:
∵∠BAC = 90°,
∴ BC 为直径 .
几何语句:
推论 直径所对的圆周角是直角.
A
B
O
C
A
B
O
C
推论 90° 的圆周角所对的弦是直径.
AB 为直径
∠ADB = 90°
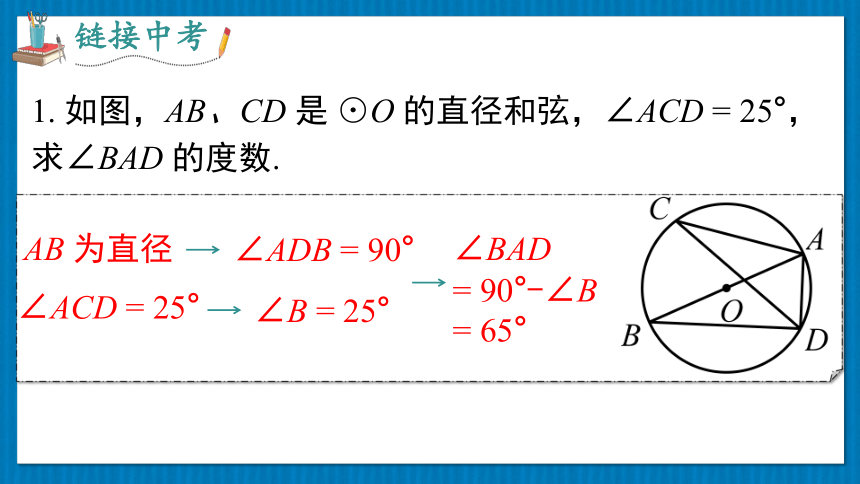
1. 如图,AB、CD 是 ⊙O 的直径和弦,∠ACD = 25°,求∠BAD 的度数.
∠ACD = 25°
∠B = 25°
∠BAD
= 90°-∠B
= 65°
链接中考
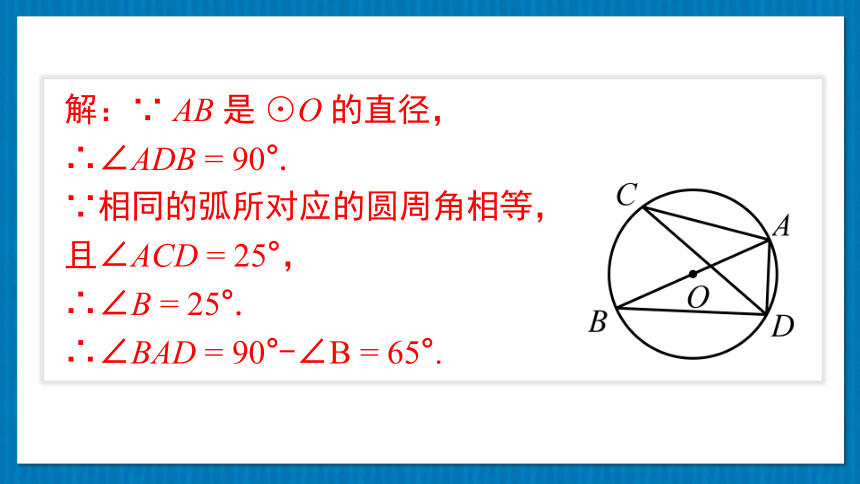
解:∵ AB 是 ⊙O 的直径,
∴∠ADB = 90°.
∵相同的弧所对应的圆周角相等,且∠ACD = 25°,
∴∠B = 25°.
∴∠BAD = 90°-∠B = 65°.
1. 如图,BD 是 ⊙O 的直径,∠CBD=30°,则∠A 的度数为( )
A.30° B.45° C.60° D.75°
解析:∵BD 是 ⊙O 的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.
故选 C.
C
A
B
O
C
练一练
(1) 如图,A,B,C,D 是 ⊙O 上的四点,AC 为⊙O 的直径,∠BAD 与 ∠BCD 之间有什么关系?为什么?
2
圆内接四边形及其性质
A
B
O
C
D
解:∠BAD 与∠BCD 互补.
∴∠BAD 与∠BCD 互补.
∴∠BAD +∠BCD = 180°.
∵∠ABC+∠BCD+∠ADC+∠BAD = 360°,
∵AC 为直径,
∴∠ABC = 90°,∠ADC = 90°.
(2) 如图,点 C 的位置发生了变化,∠BAD 与 ∠BCD 之间关系还成立吗?为什么?
A
B
O
C
D
解:∠BAD 与∠BCD 的关系仍然成立.
∴∠BAD 与∠BCD 互补.
∴∠BAD +∠BCD = 180°.
∵∠1 +∠2 = 360°,
连接 OB,OD,
则
1
2
·
O
D
B
C
A
·
O
D
B
C
A
这两个四边形ABCD有什么共同的特点?
归纳总结
四边形 ABCD 的四个顶点都在⊙O 上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
A
B
O
C
D
A
B
O
C
D
归纳总结
A
B
O
C
D
A
B
O
C
D
推论 圆内接四边形的对角互补.
根据以上讨论你能发现什么结论?
几何语句:
∵四边形 ABCD 为圆内接四边形,
∴∠BAD+∠BCD = 180°
(圆内接四边形的对角互补).
想一想
如图,∠DCE 是圆内接四边形 ABCD 的一个外角,∠A 与∠DCE 的大小有什么关系?
·
O
D
B
C
A
E
解:∠A =∠DCE
∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD = 180°.
∵∠BCD+∠DCE = 180°,
∴∠A =∠DCE.
链接中考
2.如图,四边形 ABCD 为⊙O 的内接四边形,若∠BCD = 121° ,则 ∠BOD 的度数为 ( )
A. 138°
B. 121°
C. 118°
D. 112°
C
随堂练习
1. 小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
(1)
(2)
(3)
(4)
2. 如图,⊙O的直径AB =10cm,C为⊙O上的一点,∠B=30°,求AC的长.
·
O
B
C
A
解:∵AB为直径,
∴∠BCA = 90°.
在Rt△ABC中,
∠ABC=30°,AB=10,
∴ .
3. 在圆内接四边形ABCD中,∠A与∠C的度数之比为4∶5,求∠C的度数.
·
O
D
B
C
A
解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C = 180°.
∵∠A∶∠C = 4∶5,
∴ .
即∠C的度数为100°.
基础练习
1. 如图,AB 是 ⊙O 的直径,弦 CD 交AB 与点 E,∠ADC = 26°,求∠CAB 的度数.
解:连接 BC.
∵AB 是 ⊙O 直径,
∴∠ACB = 90°.
∴∠B = ∠D = 26°.
∴∠CAB = 90° - 26° = 64°.
3. 如图,四边形 ABCD 内接⊙O ,
∠ABC = 135°,AC = 4,则⊙O 的半径为( )
A. 4 B.
C. D.
2. 如图,AB 是⊙O 的直径, C、D 是 ⊙O 的两点,且 AD = DC ,∠DAC = 25°,
求∠BAC 的度数 ( )
A. 30° B. 35°
C. 40° D. 50°
C
B
4. 如图,以 AB 为直径的⊙O 经过△ABC 的顶点 C,AE,BE 分别平分 ∠BAC 和 ∠ABC,AE 的延长线交⊙O 于点 D. 连接 BD. 判断△BDE 的形状,并证明你的结论.
能力提升
解:△BDE 为等腰直角三角形.
证明:∵ AE 平分∠BAC,BE 平分∠ABC.
∴ ∠BAE = ∠CAD = ∠CBD,∠ABE = ∠EBC.
∵ ∠BED =∠BAE +∠ABE,
∠DBE =∠DBC +∠CBE,
∴ ∠BED =∠DBE.
∴ BD = ED.
∵ AB 为直径,
∴ ∠ADB = 90°.
∴ △BDE 是等腰直角三角形.
圆周角定理
推论2
推论3
圆内接四边形的对角互补.
直径所所对的圆周角是直角;
90°的圆周角所对的弦是直径.
课后作业
P83-84
1、2、3、4
【教材P83 第1题】
知识技能
1.如图,在⊙O中,∠BOD=80°,求∠A和∠C的度数.
解:在⊙O中,∵∠BOD=80°,
∴ (圆周角定理).
又∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,
∴∠C=180°-∠A=180°-40°=140°.
2.如图,AB是⊙O的直径,∠C=15°,求∠BAD的度数.
【教材P84 第2题】
解:如图所示,连接BD.
∵∠ACD=∠ABD,∠ACD=15°
∴∠ABD=15°.
又∵AB是⊙O的直径,∴∠ADB=90°.
在Rt△ADB中,
∠BAD=90°-∠ABD=90°-15°=75°.
3.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=60°,求∠A的度数.
【教材P84 第3题】
解:如图所示,∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°,∠1=∠2=∠A,
∴∠EDC+∠CBF=180°-∠ADC+180°-∠ABC
=360°-180°=180°
∴∠E+∠1+∠2+∠F=180°,
∴2∠A+∠E+∠F=180°.
又∵∠E=40°,∠F=60°,∴2∠A=80°,∠A=40°.
4.如图,⊙O1与⊙O2都经过A,B两点,且点O2在⊙O1上.点C是
上的一点(点C不与A,B重合),AC的延长线交⊙O2于点P,连接
AB,BC,BP.
(1)根据题意将图形补充完整;
(2)当点C在 上运动时,
图中大小不变的角有哪些
(将符合要求的角都写出来)
【教材P84 第4题】
数学理解
解:(1)由题意可画图.
(2)大小不变的角有
∠APB, ∠ ACB,
∠ BCP, ∠ CBP共四个.
北师版·九年级下册
第2课时 圆周角定理的推论2,3
问题 1 什么是圆周角?
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
顶点在圆上,并且两边都和圆相交的角叫圆周角.
●O
B
A
C
D
E
问题 2 什么是圆周角定理?
圆上一条弧所对的圆周角等于它所对的圆心角的 .
即 ∠ABC = ∠AOC.
一半
C
A
B
O
C
A
B
O
C
A
B
O
复习导入
求图中角x的度数
·
A
O
B
70°
x
x =_____
C
·
O
A
B
C
D
120°
x
x =_____
35°
120°
圆周角定理 圆周角的度数等于它所对弧上的圆心角度数的一半.
复习导入
求图中角x的度数
复习导入
求图中角x的度数
·
A
O
B
60°
x
x =_____
C
·
O
A
B
C
D
20°
x
x =_____
D
60°
E
F
30°
50°
复习导入
求图中角x的度数
推论 同弧或等弧所对的圆周角相等.
探究新知
如图,BC 是⊙O 的直径,它所对的圆周角有什么特点?你能证明你的结论吗?
·
O
A
B
C
解:(猜想)直径BC所对的圆周角∠BAC=90°.
证明:∵BC为直径,
∴∠BOC=180°,
∴
如图,圆周角∠A = 90°,弦 BC 是直径吗?为什么?
解:弦 BC 是直径.
连接 OC、OB,
注意:此处不能直接连接BC,思路是先保证过点O,再证三点共线.
∴ BC 是⊙O 的一条直径.
∴ B、O、C 三点在同一直线上.
∴圆心角∠BOC=2∠A=180°.
∵圆周角∠A=90°,
A
B
O
C
归纳总结
∵ BC 为直径,
∴∠BAC = 90°.
几何语句:
∵∠BAC = 90°,
∴ BC 为直径 .
几何语句:
推论 直径所对的圆周角是直角.
A
B
O
C
A
B
O
C
推论 90° 的圆周角所对的弦是直径.
AB 为直径
∠ADB = 90°
1. 如图,AB、CD 是 ⊙O 的直径和弦,∠ACD = 25°,求∠BAD 的度数.
∠ACD = 25°
∠B = 25°
∠BAD
= 90°-∠B
= 65°
链接中考
解:∵ AB 是 ⊙O 的直径,
∴∠ADB = 90°.
∵相同的弧所对应的圆周角相等,且∠ACD = 25°,
∴∠B = 25°.
∴∠BAD = 90°-∠B = 65°.
1. 如图,BD 是 ⊙O 的直径,∠CBD=30°,则∠A 的度数为( )
A.30° B.45° C.60° D.75°
解析:∵BD 是 ⊙O 的直径,
∴∠BCD=90°.
∵∠CBD=30°,
∴∠D=60°,∴∠A=∠D=60°.
故选 C.
C
A
B
O
C
练一练
(1) 如图,A,B,C,D 是 ⊙O 上的四点,AC 为⊙O 的直径,∠BAD 与 ∠BCD 之间有什么关系?为什么?
2
圆内接四边形及其性质
A
B
O
C
D
解:∠BAD 与∠BCD 互补.
∴∠BAD 与∠BCD 互补.
∴∠BAD +∠BCD = 180°.
∵∠ABC+∠BCD+∠ADC+∠BAD = 360°,
∵AC 为直径,
∴∠ABC = 90°,∠ADC = 90°.
(2) 如图,点 C 的位置发生了变化,∠BAD 与 ∠BCD 之间关系还成立吗?为什么?
A
B
O
C
D
解:∠BAD 与∠BCD 的关系仍然成立.
∴∠BAD 与∠BCD 互补.
∴∠BAD +∠BCD = 180°.
∵∠1 +∠2 = 360°,
连接 OB,OD,
则
1
2
·
O
D
B
C
A
·
O
D
B
C
A
这两个四边形ABCD有什么共同的特点?
归纳总结
四边形 ABCD 的四个顶点都在⊙O 上,像这样的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆.
A
B
O
C
D
A
B
O
C
D
归纳总结
A
B
O
C
D
A
B
O
C
D
推论 圆内接四边形的对角互补.
根据以上讨论你能发现什么结论?
几何语句:
∵四边形 ABCD 为圆内接四边形,
∴∠BAD+∠BCD = 180°
(圆内接四边形的对角互补).
想一想
如图,∠DCE 是圆内接四边形 ABCD 的一个外角,∠A 与∠DCE 的大小有什么关系?
·
O
D
B
C
A
E
解:∠A =∠DCE
∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD = 180°.
∵∠BCD+∠DCE = 180°,
∴∠A =∠DCE.
链接中考
2.如图,四边形 ABCD 为⊙O 的内接四边形,若∠BCD = 121° ,则 ∠BOD 的度数为 ( )
A. 138°
B. 121°
C. 118°
D. 112°
C
随堂练习
1. 小明想用直角尺检查某些工件是否恰好为半圆形.下面所示的四种圆弧形,你能判断哪个是半圆形?为什么?
(1)
(2)
(3)
(4)
2. 如图,⊙O的直径AB =10cm,C为⊙O上的一点,∠B=30°,求AC的长.
·
O
B
C
A
解:∵AB为直径,
∴∠BCA = 90°.
在Rt△ABC中,
∠ABC=30°,AB=10,
∴ .
3. 在圆内接四边形ABCD中,∠A与∠C的度数之比为4∶5,求∠C的度数.
·
O
D
B
C
A
解:∵四边形ABCD是圆内接四边形,
∴∠A+∠C = 180°.
∵∠A∶∠C = 4∶5,
∴ .
即∠C的度数为100°.
基础练习
1. 如图,AB 是 ⊙O 的直径,弦 CD 交AB 与点 E,∠ADC = 26°,求∠CAB 的度数.
解:连接 BC.
∵AB 是 ⊙O 直径,
∴∠ACB = 90°.
∴∠B = ∠D = 26°.
∴∠CAB = 90° - 26° = 64°.
3. 如图,四边形 ABCD 内接⊙O ,
∠ABC = 135°,AC = 4,则⊙O 的半径为( )
A. 4 B.
C. D.
2. 如图,AB 是⊙O 的直径, C、D 是 ⊙O 的两点,且 AD = DC ,∠DAC = 25°,
求∠BAC 的度数 ( )
A. 30° B. 35°
C. 40° D. 50°
C
B
4. 如图,以 AB 为直径的⊙O 经过△ABC 的顶点 C,AE,BE 分别平分 ∠BAC 和 ∠ABC,AE 的延长线交⊙O 于点 D. 连接 BD. 判断△BDE 的形状,并证明你的结论.
能力提升
解:△BDE 为等腰直角三角形.
证明:∵ AE 平分∠BAC,BE 平分∠ABC.
∴ ∠BAE = ∠CAD = ∠CBD,∠ABE = ∠EBC.
∵ ∠BED =∠BAE +∠ABE,
∠DBE =∠DBC +∠CBE,
∴ ∠BED =∠DBE.
∴ BD = ED.
∵ AB 为直径,
∴ ∠ADB = 90°.
∴ △BDE 是等腰直角三角形.
圆周角定理
推论2
推论3
圆内接四边形的对角互补.
直径所所对的圆周角是直角;
90°的圆周角所对的弦是直径.
课后作业
P83-84
1、2、3、4
【教材P83 第1题】
知识技能
1.如图,在⊙O中,∠BOD=80°,求∠A和∠C的度数.
解:在⊙O中,∵∠BOD=80°,
∴ (圆周角定理).
又∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,
∴∠C=180°-∠A=180°-40°=140°.
2.如图,AB是⊙O的直径,∠C=15°,求∠BAD的度数.
【教材P84 第2题】
解:如图所示,连接BD.
∵∠ACD=∠ABD,∠ACD=15°
∴∠ABD=15°.
又∵AB是⊙O的直径,∴∠ADB=90°.
在Rt△ADB中,
∠BAD=90°-∠ABD=90°-15°=75°.
3.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠F=60°,求∠A的度数.
【教材P84 第3题】
解:如图所示,∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°,∠1=∠2=∠A,
∴∠EDC+∠CBF=180°-∠ADC+180°-∠ABC
=360°-180°=180°
∴∠E+∠1+∠2+∠F=180°,
∴2∠A+∠E+∠F=180°.
又∵∠E=40°,∠F=60°,∴2∠A=80°,∠A=40°.
4.如图,⊙O1与⊙O2都经过A,B两点,且点O2在⊙O1上.点C是
上的一点(点C不与A,B重合),AC的延长线交⊙O2于点P,连接
AB,BC,BP.
(1)根据题意将图形补充完整;
(2)当点C在 上运动时,
图中大小不变的角有哪些
(将符合要求的角都写出来)
【教材P84 第4题】
数学理解
解:(1)由题意可画图.
(2)大小不变的角有
∠APB, ∠ ACB,
∠ BCP, ∠ CBP共四个.
