【课时作业】1.1 探索勾股定理 (第2课时)(分层练习,含答案)2024-2025学年北师大版数学八年级上册
文档属性
| 名称 | 【课时作业】1.1 探索勾股定理 (第2课时)(分层练习,含答案)2024-2025学年北师大版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 95.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 19:03:01 | ||
图片预览


文档简介
1.1 探索勾股定理 第2课时
【基础达标】
1小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒( )
A.20根 B.14根
C.24根 D.30根
2正方形的对角线长是18,则这个正方形的面积是( )
A.9 B.18 C.162 D.81
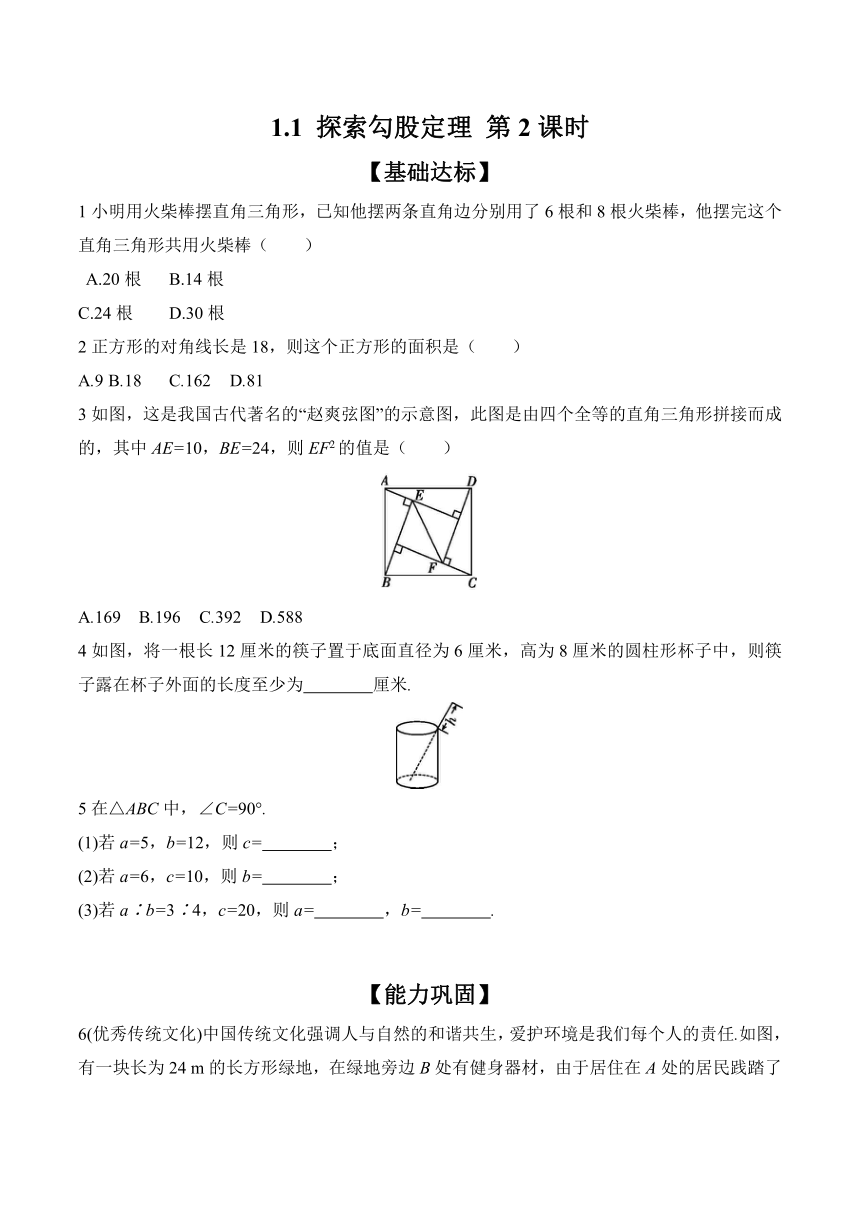
3如图,这是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成的,其中AE=10,BE=24,则EF2的值是( )
A.169 B.196 C.392 D.588
4如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为 厘米.
5在△ABC中,∠C=90°.
(1)若a=5,b=12,则c= ;
(2)若a=6,c=10,则b= ;
(3)若a∶b=3∶4,c=20,则a= ,b= .
【能力巩固】
6(优秀传统文化)中国传统文化强调人与自然的和谐共生,爱护环境是我们每个人的责任.如图,有一块长为24 m的长方形绿地,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小颖想在A处立一个标牌“少走 步,踏之何忍”,但小颖不知应填什么数字,请你帮助她填上.(假设两步为1 m)( )
A.8步 B.12步
C.16步 D.20步
7一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )
A.13 B.5
C.13或5 D.无法确定
8如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1-S2 B.S1+S2
C.2S1-S2 D.S1+2S2
9(实践教育)数学兴趣小组的同学用火柴盒研究证明勾股定理的新方法.如图,火柴盒的一个侧面ABCD旋转到CEFG的位置,连接AC,CF,AF,此时∠ABC=90°,BC=a,AB=b,AC=c.
(1)判断△ACF的形状,并说明理由.
(2)请利用直角梯形ABEF的面积证明勾股定理:a2+b2=c2.
【素养拓展】
10图1所示的弦图蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边长为a,较短的直角边长为b,斜边长为c.如图2,现将这四个全等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,求该飞镖状图案的面积.
11如图,在△ABC中,∠C=90°,AC=2.1 cm,BC=2.8 cm.
(1)求这个三角形的斜边AB的长和斜边上的高CD的长.
(2)求斜边被分成的两部分AD和BD的长.
12.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位.学习了勾股定理后,小明也绘制了一幅“赵爽弦图”(如图1所示),已知他绘制的大正方形的面积是5,且图中四个全等的直角三角形与中间的小正方形恰好能拼成如图2所示的大长方形ABCD.
(1)图中四个全等的直角三角形中较长直角边长为a,较短直角边为b,则= .(直接填数字)
(2)求图2中大长方形ABCD的周长.
参考答案
1.1 探索勾股定理 第2课时
基础达标作业
1.C 2.C 3.C
4.2
5.(1)13
(2)8
(3)12 16
能力巩固作业
6.C 7.C 8.C
9.解:(1)△ACF是等腰直角三角形.
理由:由图可知,△ABC≌△FGC,
∴∠FCG=∠ACB,AC=FC.
由题意可知,∠BCD=∠ACB+∠ACD=90°,
∴∠FCG+∠ACD=90°=∠ACF,
∴△ACF是等腰直角三角形.
(2)证明:∵BC=a,AB=b,AC=c,
∴S梯形ABEF=(EF+AB)·BE
=(a+b)(a+b)
=a2+ab+b2.
∵S梯形ABEF=S△ABC+S△CEF+S△ACF,
∴a2+ab+b2=ab+ba+c2,即a2+b2=c2,
∴a2+b2=c2.
素养拓展作业
10.解:根据题意得4(AB+AC)=24,即AB+AC=6,OB=OC=3.
在Rt△AOB中,根据勾股定理得AB2=OA2+OB2,
即(6-AC)2=32+(3+AC)2,
解得AC=1,
所以OA=3+1=4,
所以S△AOB=×3×4=6,
则该飞镖状图案的面积为24.
11.解:(1)因为△ABC中,∠C=90°,AC=2.1 cm,BC=2.8 cm,
所以AB2=AC2+BC2=2.12+2.82=12.25.
所以AB=3.5.
因为S△ABC=AC·BC=AB·CD,
所以AC·BC=AB·CD,
所以CD===1.68(cm).
(2)在Rt△ACD中,由勾股定理得
AD2+CD2=AC2,
所以AD2=AC2-CD2=2.12-1.682
=(2.1+1.68)(2.1-1.68)
=3.78×0.42=2×1.89×2×0.21
=22×9×0.21×0.21,
所以AD=2×3×0.21=1.26(cm),
所以BD=AB-AD=3.5-1.26=2.24(cm).
12.解:(1)2.
(2)设直角三角形的较长直角边长为a,较短直角边长为b,则中间的小正方形长为(a-b),
由图2可得小正方形的边长为b,
∴a-b=b,∴a=2b,
∴围成的矩形长为a+b+a=2b+b+2b=5b,
∴围成的矩形面积为5b·b=5b2.
∵矩形的面积与大正方形的面积相等,
∴5b2=5,
解得b=1(舍去负值),
∴矩形的周长为(5b+b)×2=12.
【基础达标】
1小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒( )
A.20根 B.14根
C.24根 D.30根
2正方形的对角线长是18,则这个正方形的面积是( )
A.9 B.18 C.162 D.81
3如图,这是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成的,其中AE=10,BE=24,则EF2的值是( )
A.169 B.196 C.392 D.588
4如图,将一根长12厘米的筷子置于底面直径为6厘米,高为8厘米的圆柱形杯子中,则筷子露在杯子外面的长度至少为 厘米.
5在△ABC中,∠C=90°.
(1)若a=5,b=12,则c= ;
(2)若a=6,c=10,则b= ;
(3)若a∶b=3∶4,c=20,则a= ,b= .
【能力巩固】
6(优秀传统文化)中国传统文化强调人与自然的和谐共生,爱护环境是我们每个人的责任.如图,有一块长为24 m的长方形绿地,在绿地旁边B处有健身器材,由于居住在A处的居民践踏了绿地,小颖想在A处立一个标牌“少走 步,踏之何忍”,但小颖不知应填什么数字,请你帮助她填上.(假设两步为1 m)( )
A.8步 B.12步
C.16步 D.20步
7一直角三角形的三边分别为2,3,x,那么以x为边长的正方形的面积为( )
A.13 B.5
C.13或5 D.无法确定
8如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1,小正方形面积为S2,则(a+b)2可以表示为( )
A.S1-S2 B.S1+S2
C.2S1-S2 D.S1+2S2
9(实践教育)数学兴趣小组的同学用火柴盒研究证明勾股定理的新方法.如图,火柴盒的一个侧面ABCD旋转到CEFG的位置,连接AC,CF,AF,此时∠ABC=90°,BC=a,AB=b,AC=c.
(1)判断△ACF的形状,并说明理由.
(2)请利用直角梯形ABEF的面积证明勾股定理:a2+b2=c2.
【素养拓展】
10图1所示的弦图蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边长为a,较短的直角边长为b,斜边长为c.如图2,现将这四个全等的直角三角形紧密拼接,形成飞镖状,已知外围轮廓(实线)的周长为24,OC=3,求该飞镖状图案的面积.
11如图,在△ABC中,∠C=90°,AC=2.1 cm,BC=2.8 cm.
(1)求这个三角形的斜边AB的长和斜边上的高CD的长.
(2)求斜边被分成的两部分AD和BD的长.
12.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位.学习了勾股定理后,小明也绘制了一幅“赵爽弦图”(如图1所示),已知他绘制的大正方形的面积是5,且图中四个全等的直角三角形与中间的小正方形恰好能拼成如图2所示的大长方形ABCD.
(1)图中四个全等的直角三角形中较长直角边长为a,较短直角边为b,则= .(直接填数字)
(2)求图2中大长方形ABCD的周长.
参考答案
1.1 探索勾股定理 第2课时
基础达标作业
1.C 2.C 3.C
4.2
5.(1)13
(2)8
(3)12 16
能力巩固作业
6.C 7.C 8.C
9.解:(1)△ACF是等腰直角三角形.
理由:由图可知,△ABC≌△FGC,
∴∠FCG=∠ACB,AC=FC.
由题意可知,∠BCD=∠ACB+∠ACD=90°,
∴∠FCG+∠ACD=90°=∠ACF,
∴△ACF是等腰直角三角形.
(2)证明:∵BC=a,AB=b,AC=c,
∴S梯形ABEF=(EF+AB)·BE
=(a+b)(a+b)
=a2+ab+b2.
∵S梯形ABEF=S△ABC+S△CEF+S△ACF,
∴a2+ab+b2=ab+ba+c2,即a2+b2=c2,
∴a2+b2=c2.
素养拓展作业
10.解:根据题意得4(AB+AC)=24,即AB+AC=6,OB=OC=3.
在Rt△AOB中,根据勾股定理得AB2=OA2+OB2,
即(6-AC)2=32+(3+AC)2,
解得AC=1,
所以OA=3+1=4,
所以S△AOB=×3×4=6,
则该飞镖状图案的面积为24.
11.解:(1)因为△ABC中,∠C=90°,AC=2.1 cm,BC=2.8 cm,
所以AB2=AC2+BC2=2.12+2.82=12.25.
所以AB=3.5.
因为S△ABC=AC·BC=AB·CD,
所以AC·BC=AB·CD,
所以CD===1.68(cm).
(2)在Rt△ACD中,由勾股定理得
AD2+CD2=AC2,
所以AD2=AC2-CD2=2.12-1.682
=(2.1+1.68)(2.1-1.68)
=3.78×0.42=2×1.89×2×0.21
=22×9×0.21×0.21,
所以AD=2×3×0.21=1.26(cm),
所以BD=AB-AD=3.5-1.26=2.24(cm).
12.解:(1)2.
(2)设直角三角形的较长直角边长为a,较短直角边长为b,则中间的小正方形长为(a-b),
由图2可得小正方形的边长为b,
∴a-b=b,∴a=2b,
∴围成的矩形长为a+b+a=2b+b+2b=5b,
∴围成的矩形面积为5b·b=5b2.
∵矩形的面积与大正方形的面积相等,
∴5b2=5,
解得b=1(舍去负值),
∴矩形的周长为(5b+b)×2=12.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
