11.2.1三角形的内角和定理(共22张PPT)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 11.2.1三角形的内角和定理(共22张PPT)2024-2025学年人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 19:57:51 | ||
图片预览




文档简介
(共22张PPT)
多角度探索并证明三角形的内角和定理
学 科:数学(人教版) 年 级:八年级上册
实验教学
学习目标
1
掌握三角形内角和定理,会用平行线的性质与平角定义证明三角形内角和等于180度,并能运用这些定理解决简单的问题;.
2
经历实验活动的过程,掌握三角形内角和定理,初步掌握添加辅助线的方法;
3
通过一题多证、一题多变激发学生勇于探索、合作交流的精神,提升解决问题的能力。
实验教学
三角形擂台赛
导入新课
实验教学
多角度探索三角形内角和
导入新课
问题1:你觉得三角形擂台赛谁会获得冠军?
问题2:你想怎样探索三角形内角和呢?
(请小组合作探索)
实验教学
1
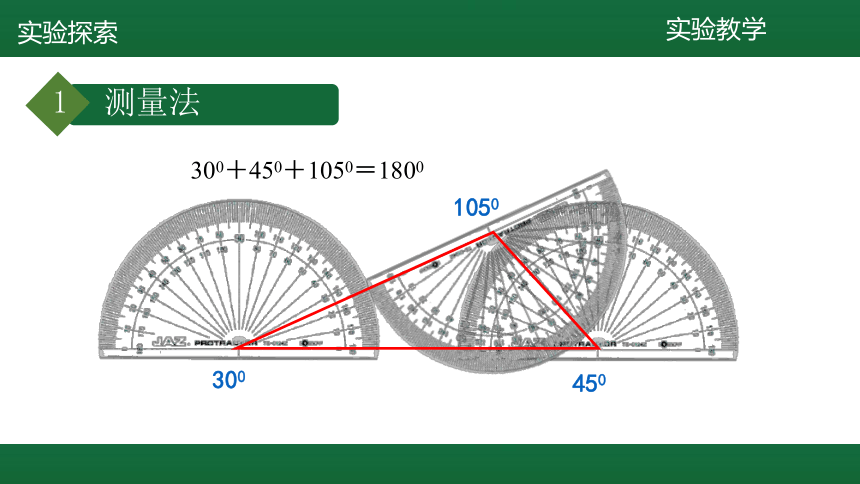
测量法
300
450
1050
300+450+1050=1800
实验探索
实验教学
2
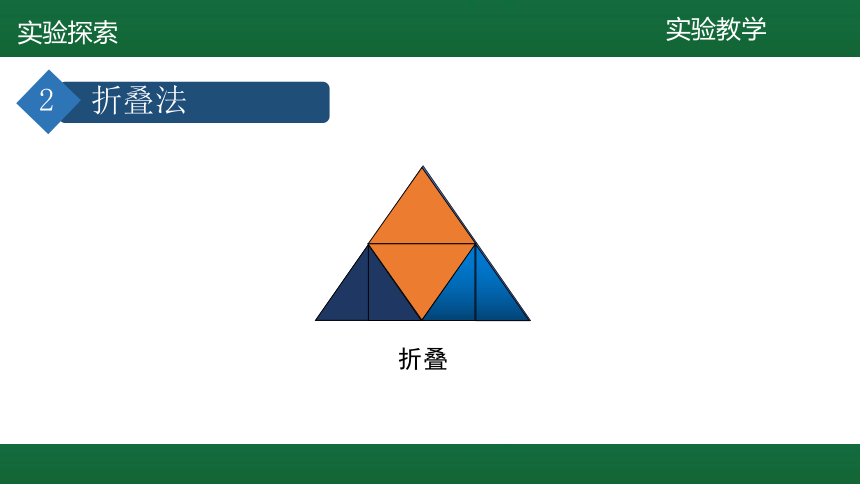
折叠法
折叠
实验探索
实验教学
3
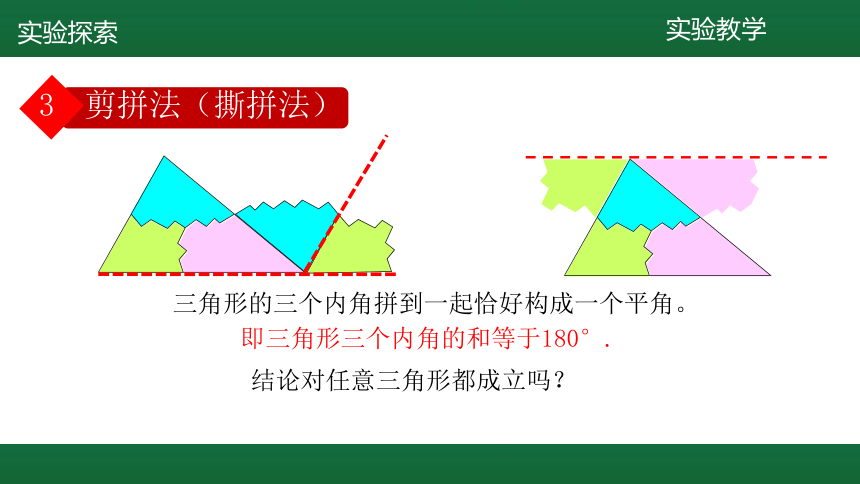
剪拼法(撕拼法)
实验探索
三角形的三个内角拼到一起恰好构成一个平角。
即三角形三个内角的和等于180°.
结论对任意三角形都成立吗?
实验教学
验证结论
C
B
A
E
D
1
2
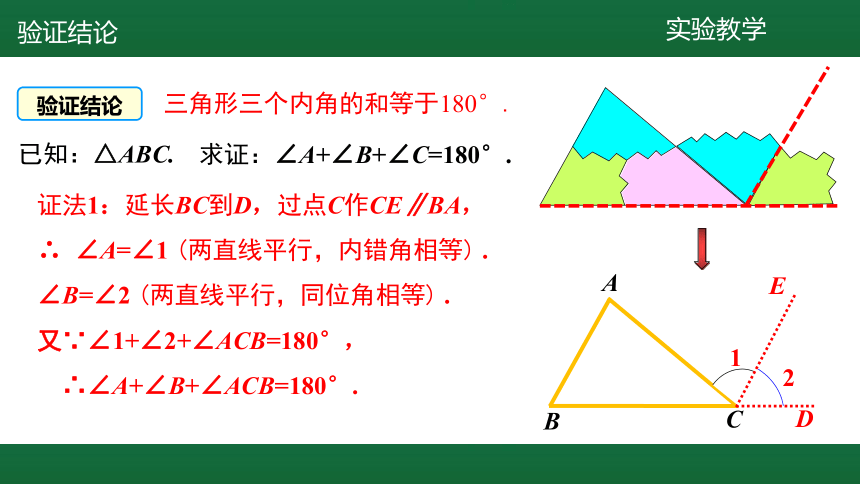
证法1:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等) .
∠B=∠2 (两直线平行,同位角相等) .
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
实验教学
验证结论
验证结论
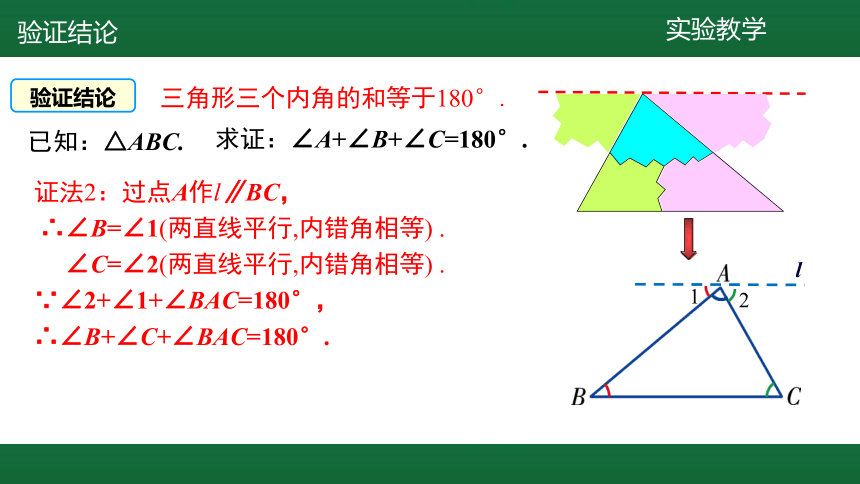
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法2:过点A作l∥BC,
∴∠B=∠1(两直线平行,内错角相等) .
∠C=∠2(两直线平行,内错角相等) .
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
实验教学
验证结论
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
C
B
A
E
1
证明:作CE//AB,
∴ ∠1=∠A(两直线平行,内错角相等).
∵ ∠BCE+∠B= ∠1+∠ACB+∠B =180°
(两直线平行,同旁内角互补).
∴ ∠A+∠ACB+∠B =180°.
实验教学
思路总结
验证结论
转化
添加辅助线
三角形内角和
平角/同旁内角
实验教学
三角形的内角和定理
三角形的内角和等于180°.
A
B
C
在△ABC中:
∠A+ ∠B+ ∠C=180°
几何语言:
得出结论
实验教学
三角形的内角和定理的运用
运用结论
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
实验教学
运用结论
【变式1】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
实验教学
例2 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
运用结论
实验教学
【变式2】已知△ABC中,∠ABC=∠C=2∠A ,BD是AC边上的高,求∠DBC的度数。
解:设∠A=x0,则∠ABC=∠C=(2x)0
A
B
C
D
∴x+2x+2x=180
(三角形内角和定理)
解得:x=36
∴∠C=2×360=720
在△BDC中,∵∠BDC=900 (三角形高的定义)
∴∠DBC=1800-900-720(三角形内角和定理)
∴∠DBC=180
运用结论
实验教学
当堂检测
1、在△ABC中,∠A:∠B:∠C =1:2:3,则∠B =( )
A. 300 B. 600 C. 900 D. 1200
2、在△ABC中,∠A =500, ∠B =800,则∠C =( )
A. 400 B. 500 C. 100 D. 1100
3、在△ABC中,∠A =800, ∠B =∠C,则∠B =( )
A. 500 B. 400 C. 100 D. 450
B
B
A
实验教学
当堂检测
4.在△ABC中,∠A=∠B+∠C,则下列对△ABC形状的判断正确的是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
B
实验教学
当堂检测
5.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-60°=120°.
实验教学
课堂小结
三角形的
内角和定理
证明
内容
三角形内角和等于180 °
添加辅助线
三角形内角和
转化
平角/同旁内角
实验教学
布置作业
1
请同学课下思考证明三角形内角和的方法还有哪些?
智勇大比拼!
2
如图所示:求∠A+∠B+∠C+∠D+∠E的度数?
E
D
C
B
A
在数学中最令我欣喜的,是那些能够被证明的东西。
——罗素
感谢聆听!
多角度探索并证明三角形的内角和定理
学 科:数学(人教版) 年 级:八年级上册
实验教学
学习目标
1
掌握三角形内角和定理,会用平行线的性质与平角定义证明三角形内角和等于180度,并能运用这些定理解决简单的问题;.
2
经历实验活动的过程,掌握三角形内角和定理,初步掌握添加辅助线的方法;
3
通过一题多证、一题多变激发学生勇于探索、合作交流的精神,提升解决问题的能力。
实验教学
三角形擂台赛
导入新课
实验教学
多角度探索三角形内角和
导入新课
问题1:你觉得三角形擂台赛谁会获得冠军?
问题2:你想怎样探索三角形内角和呢?
(请小组合作探索)
实验教学
1
测量法
300
450
1050
300+450+1050=1800
实验探索
实验教学
2
折叠法
折叠
实验探索
实验教学
3
剪拼法(撕拼法)
实验探索
三角形的三个内角拼到一起恰好构成一个平角。
即三角形三个内角的和等于180°.
结论对任意三角形都成立吗?
实验教学
验证结论
C
B
A
E
D
1
2
证法1:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等) .
∠B=∠2 (两直线平行,同位角相等) .
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
实验教学
验证结论
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法2:过点A作l∥BC,
∴∠B=∠1(两直线平行,内错角相等) .
∠C=∠2(两直线平行,内错角相等) .
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
实验教学
验证结论
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
C
B
A
E
1
证明:作CE//AB,
∴ ∠1=∠A(两直线平行,内错角相等).
∵ ∠BCE+∠B= ∠1+∠ACB+∠B =180°
(两直线平行,同旁内角互补).
∴ ∠A+∠ACB+∠B =180°.
实验教学
思路总结
验证结论
转化
添加辅助线
三角形内角和
平角/同旁内角
实验教学
三角形的内角和定理
三角形的内角和等于180°.
A
B
C
在△ABC中:
∠A+ ∠B+ ∠C=180°
几何语言:
得出结论
实验教学
三角形的内角和定理的运用
运用结论
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:由∠BAC=40 °, AD是△ABC的角平分线,得
∠BAD= ∠BAC=20 °.
在△ABD中,∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
实验教学
运用结论
【变式1】如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:∵∠A=50°,∠B=70°,
∴∠ACB=180°-∠A-∠B=60°.
∵CD是∠ACB的平分线,
∴∠BCD= ∠ACB=30°.
∵DE∥BC,
∴∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
实验教学
例2 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解: 设∠B为x°,则∠A为(3x)°,∠C为(x + 15)°, 从而有
3x + x +(x + 15)= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
几何问题借助方程来解. 这是一个重要的数学思想.
运用结论
实验教学
【变式2】已知△ABC中,∠ABC=∠C=2∠A ,BD是AC边上的高,求∠DBC的度数。
解:设∠A=x0,则∠ABC=∠C=(2x)0
A
B
C
D
∴x+2x+2x=180
(三角形内角和定理)
解得:x=36
∴∠C=2×360=720
在△BDC中,∵∠BDC=900 (三角形高的定义)
∴∠DBC=1800-900-720(三角形内角和定理)
∴∠DBC=180
运用结论
实验教学
当堂检测
1、在△ABC中,∠A:∠B:∠C =1:2:3,则∠B =( )
A. 300 B. 600 C. 900 D. 1200
2、在△ABC中,∠A =500, ∠B =800,则∠C =( )
A. 400 B. 500 C. 100 D. 1100
3、在△ABC中,∠A =800, ∠B =∠C,则∠B =( )
A. 500 B. 400 C. 100 D. 450
B
B
A
实验教学
当堂检测
4.在△ABC中,∠A=∠B+∠C,则下列对△ABC形状的判断正确的是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
B
实验教学
当堂检测
5.如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
解:∵△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-60°=120°.
实验教学
课堂小结
三角形的
内角和定理
证明
内容
三角形内角和等于180 °
添加辅助线
三角形内角和
转化
平角/同旁内角
实验教学
布置作业
1
请同学课下思考证明三角形内角和的方法还有哪些?
智勇大比拼!
2
如图所示:求∠A+∠B+∠C+∠D+∠E的度数?
E
D
C
B
A
在数学中最令我欣喜的,是那些能够被证明的东西。
——罗素
感谢聆听!
