11.1与三角形有关的线段 课时作业(含详解)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 11.1与三角形有关的线段 课时作业(含详解)2024—2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 332.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 11:45:56 | ||
图片预览



文档简介
11.1与三角形有关的线段 课时作业2024—2025学年人教版八年级上册数学
一、单选题
1.下列长度的线段能构成三角形的是( )
A.3,3,6 B.2,1,5 C.5,3,4 D.3,2,7
2.现有长度为和的两根小棒,请你再找一根小棒,并以这三根小棒为边围成一个三角形,则下列长度的小棒可选的是( )
A. B. C. D.
3.三角形的三边长分别是4,8,,则的取值可能是( )
A.3 B.4 C.5 D.6
4.等腰三角形的周长为12,则腰长a的取值范围是( )
A.a>6 B.a<3
C.45.已知线段a、b、c分别为三角形的三边长,则化简|a+c﹣b|﹣|c﹣a﹣b|的结果为( )
A.2c﹣2b B.2b﹣2c C.﹣2a D.2a
6.下列长度的三条线段,能组成三角形的是( )
A. B. C. D.
7.从长度为 1 、3 、5 、7 的四条线段中,任意取出三条线段,能围成三角形的是( )
A.1 ,3 ,5 B.1 ,3 ,7 C.1 ,5 ,7 D.3 ,5 ,7
8.若某三角形的两边长分别为5和9,则该三角形第三边的长可能是( )
A.4 B.5 C.14 D.15
二、填空题
9.如图,在△ABC中,点D、E分别为边BC、AC上的点,将△CDE沿DE翻折得到△C′DE,使C′D∥AB.若∠A=75°,∠C=45°,则∠C′EA的大小为 °.
10.若三角形三条边长分别是1,a,其中a为整数,则a的取值为 .
11.已知一个三角形的三边长为4,7,x,则x的取值范围是 .
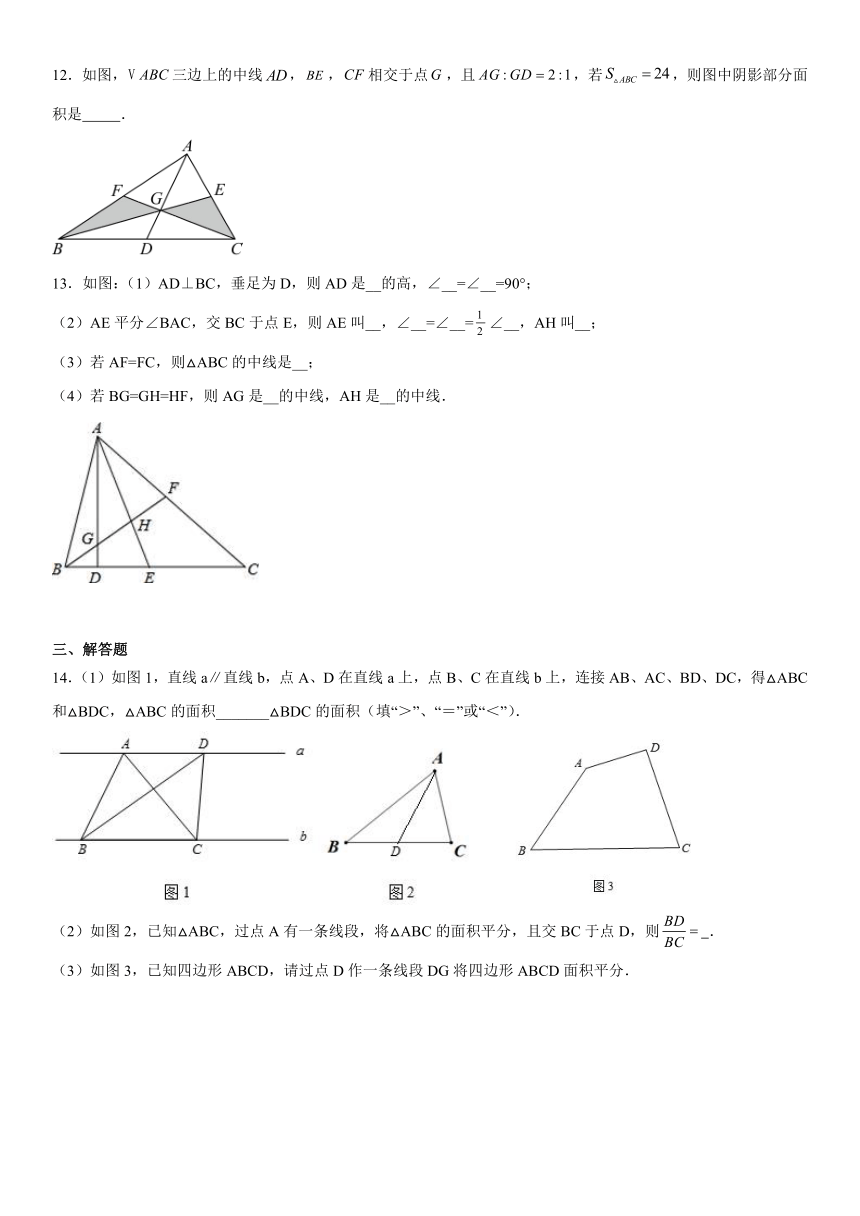
12.如图,三边上的中线,,相交于点,且,若,则图中阴影部分面积是 .
13.如图:(1)AD⊥BC,垂足为D,则AD是__的高,∠__=∠__=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫__,∠__=∠__=∠__,AH叫__;
(3)若AF=FC,则△ABC的中线是__;
(4)若BG=GH=HF,则AG是__的中线,AH是__的中线.
三、解答题
14.(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则 .
(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
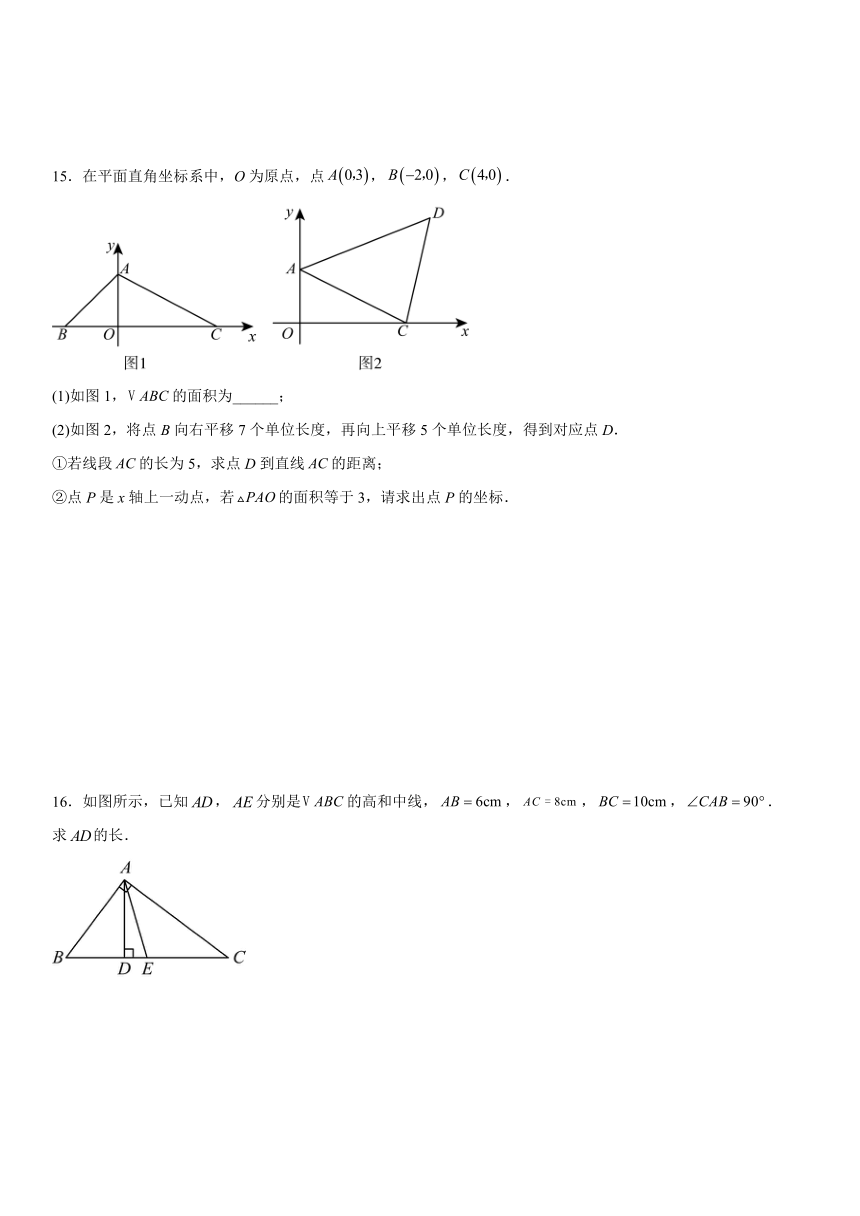
15.在平面直角坐标系中,O为原点,点,,.
(1)如图1,的面积为______;
(2)如图2,将点B向右平移7个单位长度,再向上平移5个单位长度,得到对应点D.
①若线段的长为5,求点D到直线的距离;
②点P是x轴上一动点,若的面积等于3,请求出点P的坐标.
16.如图所示,已知,分别是的高和中线,,,,.
求的长.
17.已知三角形的三条边长为和.
(1)若6是最短边长.求的取值范围;
(2)若为整数,求三角形周长的最大值.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C C D D A C D B
1.C
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析判断即可.
【详解】解:A、,不能构成三角形,该选项不符合题意;
B、,不能构成三角形,该选项不符合题意;
C、,能构成三角形,该选项符合题意;
D、,不能构成三角形,该选项不符合题意.
故选:C.
【点睛】此题主要考查了三角形三边关系,根据第三边的范围是:大于已知的两边的差,而小于两边的和是解决问题的关键.
2.C
【分析】根据三角形的三边关系可得第三根小棒的长度,再逐一分析可得答案.
【详解】解:设第三根小棒的长度为xcm,
由题意得:,
解得:,
C选项符合题意,
故选C.
【点睛】此题主要考查了三角形的三边关系,关键是掌握三边关系定理:三角形两边之和大于第三边.角形的两边差小于第三边.
3.D
【分析】根据三角形的三边关系列式确定a的取值范围即可.
【详解】解:根据题意得:,
解得,
只有6适合,
故选:D.
【点睛】本题考查了三角形的三边关系,解一元一次不等式组,解题的关键是根据三角形的三边关系确定a的取值范围,难度不大.
4.D
【分析】设等腰三角形的腰长为a,则其底边长为:12-2a,根据三角形三边关系列出不等式组,解不等式组即可.
【详解】设等腰三角形的腰长为a,则其底边长为:12-2a.
∵12-2a-a<a<12-2a+a,
∴3<a<6.
故选D.
【点睛】本题考查了等腰三角形的性质及三角形三边关系的综合运用,根据等腰三角形的性质及三角形的三边关系列出不等式组12-2a-a<a<12-2a+a是解决问题的关键.
5.A
【分析】利用三边关系判断出a+c﹣b,c﹣a﹣b的正负性,再利用绝对值的性质进行化简计算即可.
【详解】解:∵a+c﹣b>0,c﹣a﹣b<0,
∴|a+c﹣b|﹣|c﹣a﹣b|
=(a+c﹣b)﹣(﹣c+a+b)
=a+c﹣b+c﹣a﹣b
=2c﹣2b,
故选:A.
【点睛】此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边.
6.C
【分析】三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.若两条较短边的和小于或等于最长边,则不能构成三角形,据此分析即可.
【详解】A、,不满足三角形的三边关系,不符题意
B、,不满足三角形的三边关系,不符题意
C、,满足三角形的三边关系,符合题意
D、,不满足三角形的三边关系,不符题意
故选:C.
【点睛】本题考查了三角形的三边关系定理,熟记三角形的三边关系是解题关键.
7.D
【分析】根据构成三角形的条件逐一判断即可.
【详解】解:A、∵,∴不能构成三角形,不符合题意;
B、∵,∴不能构成三角形,不符合题意;
C、∵,∴不能构成三角形,不符合题意;
D、∵,∴能构成三角形,符合题意;
故选D.
【点睛】本题主要考查了构成三角形的条件,熟知三角形中任意两边之差小于第三边,任意两边之和大于第三边是解题的关键.
8.B
【分析】根据三角形的三边关系即可得.
【详解】设该三角形第三边的长为,
由三角形的三边关系得:,即,
观察四个选项可知,只有选项符合,
故选:B.
【点睛】本题考查了三角形的三边关系,熟练掌握三角形的三边关系是解题关键.
9.30
【分析】由C′D∥AB得出∠DGE=∠A=75°,由折叠性质可知,∠C'=∠C=45°,再根据三角形外角性质求出∠C′EA=∠DGE-∠C'=75°-45°=30°.
【详解】解:如图,
∵C′D∥AB,
∴∠DGE=∠A=75°,
由折叠性质可知,∠C'=∠C=45°,
∴∠C′EA=∠DGE-∠C'=75°-45°=30°,
故答案为30.
【点睛】本题考查了翻折变换的知识及三角形外角的性质,解答本题的关键是求出∠DGE的度数是解题的关键.
10.5
【分析】根据三角形三边关系求解即可.
【详解】解:∵三角形的两边长分别为1和5,
∴第三边长a的取值范围是:,即:,
∴整数a的值为5.
故答案为5.
【点睛】本题考查三角形三边关系.掌握三角形任意两边之和大于第三边,任意两边之差小于第三边是解题关键.
11.
【分析】本题考查了三角形的三边关系,掌握任意两边之和大于第三边,任意两边之差小于第三边是解题的关键.
【详解】解:三角形的三边长分别为4,7,,
,即.
故答案为:.
12.8
【分析】本题考查三角形的重心、三角形的面积,根据“同高的两个三角形,其面积比等于底边长之比”计算即可,掌握“同高的两个三角形,其面积比等于底边长之比”是解题的关键.
【详解】解:∵是边上的中线,
∴,
∴,
∵,
∴,,
∵是边上的中线,
∴,
∴,
∵是边上的中线,
∴,
∴,
∴.
故答案为:8.
13. BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【详解】试题解析:(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线,AH是△AGF的中线.
故答案为(1)BC边上,ADB,ADC;(2)∠BAC的角平分线,BAE,CAE,BAC,∠BAF的角平分线;(3)BF;(4)△ABH,△AGF.
14.(1)=;(2);(3)见解析
【分析】(1)根据同底等高即可得到三角形面积相等;
(2)根据中线的性质即可求解;
(3)先利用平行线得到面积相等,再根据中线的性质即可求解.
【详解】解:(1)∵a∥b,
∴△ABC和△BDC同底等高,
∴△ABC的面积等于△BDC的面积
故答案为:=;
(2)∵AD将△ABC的面积平分,,
∴AD是△ABC的中线,
∴
故答案为;
(3)如图,连接BD,过点A作BD的平行线AE,延长CB交AE于点F,取FC中点G,连接DG,DG为所求线段.
【点睛】此题主要考查中线与平行线的应用,解题的关键是熟知三角形的面积求解与中线平分面积的性质.
15.(1)9
(2)①点D到直线的距离为;②点P的坐标为或
【分析】(1)由题意可得、的长,由三角形面积公式即可求得;
(2)①过点D作轴于E,由平移可确定点D的坐标,由求出的面积,然后再求出距离即可;
②由面积可得,根据点P在x轴上的位置即可求得点P的坐标.
【详解】(1)解:∵点,,,
∴,,,
∴,
∴
故答案为:9;
(2)解:①如图,过点D作轴于E,
由题意,点D坐标为,则点E坐标为,
∴,,,
∴
,
∵线段的长为5,
∴点D到直线的距离为:
;
②由题意得:,
即
∴
∵点P在x轴上
∴点P的坐标为或.
【点睛】本题考查了坐标与图形,点的平移,平面直角坐标系中求三角形面积,平面直角坐标系中求三角形面积时,如果三角形中无一边与坐标轴平行,则常常用割补的方法,使得三角形表示为易于求得面积的三角形或四边形面积的和或差.注意(2)问中点P的坐标有两种情况,不要忽略x轴负半轴上的情况.
16.
【分析】本题主要考查了三角形的面积公式,等式的性质等知识点,熟练掌握三角形的面积公式是解题的关键.
根据三角形的面积公式可得,然后利用等式的性质即可得出答案.
【详解】解:,是边上的高,
,
,
即:的长为.
17.(1)
(2)
【分析】本题主要考查了三角形三边关系的应用:
(1)三角形中,任意两边之差小于第三边,任意两边之和大于第三边,据此可得,再由是最短边长,可得;
(2)根据(1)所求可得,则的最大值为14,据此根据三角形周长计算公式求解即可.
【详解】(1)解:由题意得:,即,
是最短边长,
,
的取值范围是;
(2)解:由(1)可知,,
为整数,
的最大值为14,
三角形周长的最大值为.
一、单选题
1.下列长度的线段能构成三角形的是( )
A.3,3,6 B.2,1,5 C.5,3,4 D.3,2,7
2.现有长度为和的两根小棒,请你再找一根小棒,并以这三根小棒为边围成一个三角形,则下列长度的小棒可选的是( )
A. B. C. D.
3.三角形的三边长分别是4,8,,则的取值可能是( )
A.3 B.4 C.5 D.6
4.等腰三角形的周长为12,则腰长a的取值范围是( )
A.a>6 B.a<3
C.4
A.2c﹣2b B.2b﹣2c C.﹣2a D.2a
6.下列长度的三条线段,能组成三角形的是( )
A. B. C. D.
7.从长度为 1 、3 、5 、7 的四条线段中,任意取出三条线段,能围成三角形的是( )
A.1 ,3 ,5 B.1 ,3 ,7 C.1 ,5 ,7 D.3 ,5 ,7
8.若某三角形的两边长分别为5和9,则该三角形第三边的长可能是( )
A.4 B.5 C.14 D.15
二、填空题
9.如图,在△ABC中,点D、E分别为边BC、AC上的点,将△CDE沿DE翻折得到△C′DE,使C′D∥AB.若∠A=75°,∠C=45°,则∠C′EA的大小为 °.
10.若三角形三条边长分别是1,a,其中a为整数,则a的取值为 .
11.已知一个三角形的三边长为4,7,x,则x的取值范围是 .
12.如图,三边上的中线,,相交于点,且,若,则图中阴影部分面积是 .
13.如图:(1)AD⊥BC,垂足为D,则AD是__的高,∠__=∠__=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫__,∠__=∠__=∠__,AH叫__;
(3)若AF=FC,则△ABC的中线是__;
(4)若BG=GH=HF,则AG是__的中线,AH是__的中线.
三、解答题
14.(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则 .
(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
15.在平面直角坐标系中,O为原点,点,,.
(1)如图1,的面积为______;
(2)如图2,将点B向右平移7个单位长度,再向上平移5个单位长度,得到对应点D.
①若线段的长为5,求点D到直线的距离;
②点P是x轴上一动点,若的面积等于3,请求出点P的坐标.
16.如图所示,已知,分别是的高和中线,,,,.
求的长.
17.已知三角形的三条边长为和.
(1)若6是最短边长.求的取值范围;
(2)若为整数,求三角形周长的最大值.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C C D D A C D B
1.C
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析判断即可.
【详解】解:A、,不能构成三角形,该选项不符合题意;
B、,不能构成三角形,该选项不符合题意;
C、,能构成三角形,该选项符合题意;
D、,不能构成三角形,该选项不符合题意.
故选:C.
【点睛】此题主要考查了三角形三边关系,根据第三边的范围是:大于已知的两边的差,而小于两边的和是解决问题的关键.
2.C
【分析】根据三角形的三边关系可得第三根小棒的长度,再逐一分析可得答案.
【详解】解:设第三根小棒的长度为xcm,
由题意得:,
解得:,
C选项符合题意,
故选C.
【点睛】此题主要考查了三角形的三边关系,关键是掌握三边关系定理:三角形两边之和大于第三边.角形的两边差小于第三边.
3.D
【分析】根据三角形的三边关系列式确定a的取值范围即可.
【详解】解:根据题意得:,
解得,
只有6适合,
故选:D.
【点睛】本题考查了三角形的三边关系,解一元一次不等式组,解题的关键是根据三角形的三边关系确定a的取值范围,难度不大.
4.D
【分析】设等腰三角形的腰长为a,则其底边长为:12-2a,根据三角形三边关系列出不等式组,解不等式组即可.
【详解】设等腰三角形的腰长为a,则其底边长为:12-2a.
∵12-2a-a<a<12-2a+a,
∴3<a<6.
故选D.
【点睛】本题考查了等腰三角形的性质及三角形三边关系的综合运用,根据等腰三角形的性质及三角形的三边关系列出不等式组12-2a-a<a<12-2a+a是解决问题的关键.
5.A
【分析】利用三边关系判断出a+c﹣b,c﹣a﹣b的正负性,再利用绝对值的性质进行化简计算即可.
【详解】解:∵a+c﹣b>0,c﹣a﹣b<0,
∴|a+c﹣b|﹣|c﹣a﹣b|
=(a+c﹣b)﹣(﹣c+a+b)
=a+c﹣b+c﹣a﹣b
=2c﹣2b,
故选:A.
【点睛】此题主要考查了三角形的三边关系,关键是掌握三角形两边之和大于第三边.
6.C
【分析】三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.若两条较短边的和小于或等于最长边,则不能构成三角形,据此分析即可.
【详解】A、,不满足三角形的三边关系,不符题意
B、,不满足三角形的三边关系,不符题意
C、,满足三角形的三边关系,符合题意
D、,不满足三角形的三边关系,不符题意
故选:C.
【点睛】本题考查了三角形的三边关系定理,熟记三角形的三边关系是解题关键.
7.D
【分析】根据构成三角形的条件逐一判断即可.
【详解】解:A、∵,∴不能构成三角形,不符合题意;
B、∵,∴不能构成三角形,不符合题意;
C、∵,∴不能构成三角形,不符合题意;
D、∵,∴能构成三角形,符合题意;
故选D.
【点睛】本题主要考查了构成三角形的条件,熟知三角形中任意两边之差小于第三边,任意两边之和大于第三边是解题的关键.
8.B
【分析】根据三角形的三边关系即可得.
【详解】设该三角形第三边的长为,
由三角形的三边关系得:,即,
观察四个选项可知,只有选项符合,
故选:B.
【点睛】本题考查了三角形的三边关系,熟练掌握三角形的三边关系是解题关键.
9.30
【分析】由C′D∥AB得出∠DGE=∠A=75°,由折叠性质可知,∠C'=∠C=45°,再根据三角形外角性质求出∠C′EA=∠DGE-∠C'=75°-45°=30°.
【详解】解:如图,
∵C′D∥AB,
∴∠DGE=∠A=75°,
由折叠性质可知,∠C'=∠C=45°,
∴∠C′EA=∠DGE-∠C'=75°-45°=30°,
故答案为30.
【点睛】本题考查了翻折变换的知识及三角形外角的性质,解答本题的关键是求出∠DGE的度数是解题的关键.
10.5
【分析】根据三角形三边关系求解即可.
【详解】解:∵三角形的两边长分别为1和5,
∴第三边长a的取值范围是:,即:,
∴整数a的值为5.
故答案为5.
【点睛】本题考查三角形三边关系.掌握三角形任意两边之和大于第三边,任意两边之差小于第三边是解题关键.
11.
【分析】本题考查了三角形的三边关系,掌握任意两边之和大于第三边,任意两边之差小于第三边是解题的关键.
【详解】解:三角形的三边长分别为4,7,,
,即.
故答案为:.
12.8
【分析】本题考查三角形的重心、三角形的面积,根据“同高的两个三角形,其面积比等于底边长之比”计算即可,掌握“同高的两个三角形,其面积比等于底边长之比”是解题的关键.
【详解】解:∵是边上的中线,
∴,
∴,
∵,
∴,,
∵是边上的中线,
∴,
∴,
∵是边上的中线,
∴,
∴,
∴.
故答案为:8.
13. BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【详解】试题解析:(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线,AH是△AGF的中线.
故答案为(1)BC边上,ADB,ADC;(2)∠BAC的角平分线,BAE,CAE,BAC,∠BAF的角平分线;(3)BF;(4)△ABH,△AGF.
14.(1)=;(2);(3)见解析
【分析】(1)根据同底等高即可得到三角形面积相等;
(2)根据中线的性质即可求解;
(3)先利用平行线得到面积相等,再根据中线的性质即可求解.
【详解】解:(1)∵a∥b,
∴△ABC和△BDC同底等高,
∴△ABC的面积等于△BDC的面积
故答案为:=;
(2)∵AD将△ABC的面积平分,,
∴AD是△ABC的中线,
∴
故答案为;
(3)如图,连接BD,过点A作BD的平行线AE,延长CB交AE于点F,取FC中点G,连接DG,DG为所求线段.
【点睛】此题主要考查中线与平行线的应用,解题的关键是熟知三角形的面积求解与中线平分面积的性质.
15.(1)9
(2)①点D到直线的距离为;②点P的坐标为或
【分析】(1)由题意可得、的长,由三角形面积公式即可求得;
(2)①过点D作轴于E,由平移可确定点D的坐标,由求出的面积,然后再求出距离即可;
②由面积可得,根据点P在x轴上的位置即可求得点P的坐标.
【详解】(1)解:∵点,,,
∴,,,
∴,
∴
故答案为:9;
(2)解:①如图,过点D作轴于E,
由题意,点D坐标为,则点E坐标为,
∴,,,
∴
,
∵线段的长为5,
∴点D到直线的距离为:
;
②由题意得:,
即
∴
∵点P在x轴上
∴点P的坐标为或.
【点睛】本题考查了坐标与图形,点的平移,平面直角坐标系中求三角形面积,平面直角坐标系中求三角形面积时,如果三角形中无一边与坐标轴平行,则常常用割补的方法,使得三角形表示为易于求得面积的三角形或四边形面积的和或差.注意(2)问中点P的坐标有两种情况,不要忽略x轴负半轴上的情况.
16.
【分析】本题主要考查了三角形的面积公式,等式的性质等知识点,熟练掌握三角形的面积公式是解题的关键.
根据三角形的面积公式可得,然后利用等式的性质即可得出答案.
【详解】解:,是边上的高,
,
,
即:的长为.
17.(1)
(2)
【分析】本题主要考查了三角形三边关系的应用:
(1)三角形中,任意两边之差小于第三边,任意两边之和大于第三边,据此可得,再由是最短边长,可得;
(2)根据(1)所求可得,则的最大值为14,据此根据三角形周长计算公式求解即可.
【详解】(1)解:由题意得:,即,
是最短边长,
,
的取值范围是;
(2)解:由(1)可知,,
为整数,
的最大值为14,
三角形周长的最大值为.
