第五章 一元一次方程 单元复习 课件(共28张PPT)
文档属性
| 名称 | 第五章 一元一次方程 单元复习 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 15:10:57 | ||
图片预览








文档简介
(共28张PPT)
复习与小结
人教版七年级上册
第五章 一元一次方程
复习目标
重点
难点
从实际问题中抽象出数学模型.
理解配套问题、工程问题中的数量关系.
(1) 根据实际问题中数量关系列方程解决问题,并进一步熟练掌握一元一次方程的解法.
(2)培养数学建模能力,体会方程模型在实际问题求解过程中的优势.
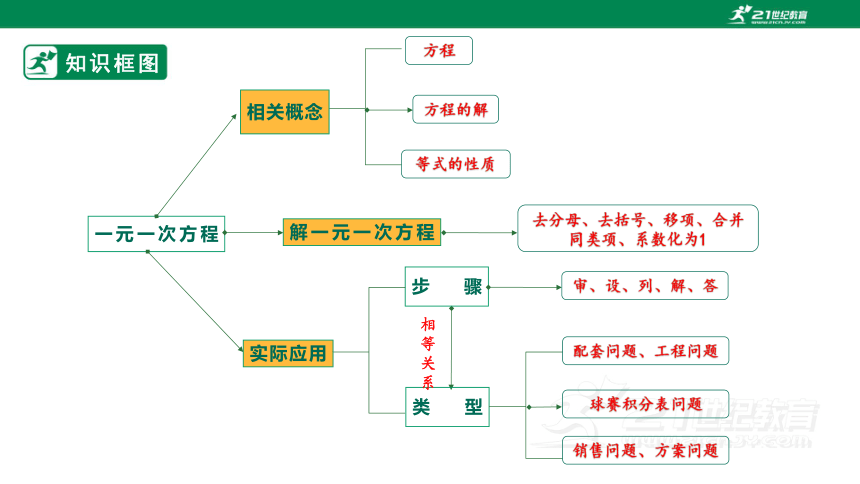
知识框图
一元一次方程
实际应用
步骤
类型
审、设、列、解、答
相关概念
相等关系
方程
方程的解
等式的性质
解一元一次方程
去分母、去括号、移项、合并同类项、系数化为1
配套问题、工程问题
球赛积分表问题
销售问题、方案问题
知识梳理
知识点1 方程相关概念
(1)含有未知数的______叫做方程.
等式
(2)一般地,使方程左、右两边的值相等的______的值,叫做方程的解.
未知数
(3)一般地,如果方程中只含有_____个未知数(元),且含有未知数的式子都是_______,未知数的次数都是______,这样的方程叫做一元一次方程.
一
整式
1
知识梳理
1.下列各式中,属于方程的是( )
2.若x=2是方程4x+m=6的解,则m的值为_______.
3.已知关于x的方程 是一元一次方程,则a的值为_______.
D
-2
2
知识梳理
知识点2 等式的性质
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
巩固提升
1.如果 ,那么根据等式的性质,下列变形错误的是( )
D
2.已知-4m+3=-4n+3,根据等式的性质,则m_____n.
=
知识梳理
知识点3 解一元一次方程
(1)解一元一次方程的一般步骤包括:______、去括号、______、合并同类项、__________.
去分母
移项
系数化为1
(2)去分母:一元一次方程中如果有分母,利用等式的性质_____,将方程的两边都乘各分母的__________,从而去掉分母.
2
最小公倍数
(3)移项:把等式一边的某项________移到另一边,叫做移项,其依据是___________.
变号后
等式的性质1
(4)系数化为1:利用等式的性质_____,将方程两边除以未知数的系数,将未知数的系数化为1.
2
巩固提升
1.解方程 ,以下去括号正确的是( )
B
2.已知代数式2+x和-x-6的值相等,则x的值为______.
-4
3.若多项式 互为相反数,则a的值为______.
-3
巩固提升
4.解下列方程.
解:
解:
知识梳理
知识点4 实际问题
(1)用一元一次方程解决实际问题的基本过程包括:设______、列方程、______、检验所得结果、确定答案.正确分析问题中的_______关系是列方程的基础.
未知数
解方程
相等
(2)配套问题中的基本相等关系:
若m个A物品与n个B物品配成一套,则_____×A数量=____×B的数量.
n
m
知识梳理
知识点4 实际问题
(3)工程问题中的基本相等关系:
工作量=________×工作时间.
工作效率
(4)销售问题中的基本相等关系:
售价=_____+进价=进价×(1+利润率)
利润=_____-进价.
利润
售价
利润率=(利润÷进价)×100%.
巩固提升
1. 某种商品因换季准备打折出售,如果按原定价的七五折出售,将赔25元,而按原定价的九折出售,将赚20元,则这种商品的原价是( )
A.500元 B.400元
C.300元 D.200元
D
巩固提升
2.某次数学竞赛共有20道题,已知做对一道得4分,做错一道或不做扣1分,某同学最后的得分是55分,则他做对了( )
A.16道 B.15道 C.14道 D.13道
3.一项工程由甲单独完成需要8天,由乙单独完成需要10天.现在由甲先做3天,剩下的甲乙合作完成.若设完成此项工程共需x天,可列方程为______________.
B
巩固提升
4.某车间有84名工人,平均每人每天加工16个大齿轮或10个小齿轮,已知1个大齿轮和2个小齿轮配套.为使每天加工的大、小齿轮刚好配套,应该每天安排多少名工人加工大齿轮?
解:设应该每天安排x名工人加工大齿轮,则(84-x)名工人加工小齿轮.
根据题意得:10(84-x)=2×16x
解得:x=20
所以,84-x=64
答:应该每天安排20名工人加工大齿轮.
综合练习
1.下列方程是一元一次方程的是( )
C
2.已知关于x的方程 的解是x=3,则k的值是( )
C
综合练习
3.下列方程变形正确的是( )
D
综合练习
4.阅读课上,语文老师将一些书分给各小组,若每个小组分8本,则剩余3本;若每个小组分9本,则缺少2本,问有几个小组?设有x个小组,可列方程为( )
B
综合练习
5.对于任意有理数a,b规定 ,若 ,则x的值为( )
A
综合练习
6.解下列方程.
解:
解:
综合练习
7.已知 与 都是关于x的一元一次方程,且有相同的解,求a的值.
解:
综合练习
8.一项工程,由甲单独做需要10天完成,乙单独做需要15天完成.若甲先做5天,再由甲乙合作,共完成全部工程的三分之二,则甲乙合作多少天?
解:设甲乙合作x天.
根据题意得,
解得,x= 1
答:甲乙合作1天.
综合练习
9.某服装店,打折销售服装,若每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元.每件服装的标价多少元?每件服装的成本价多少元?
解:设每件服装的标价为x元.
根据题意得,
解得,x=200
所以,0.5x+20=120
答:每件服装的标价为200元. 成本为120元.
综合练习
10.为鼓励居民节约用水,采用分段计费的方法收取水费:当月用水量不超过20立方米时,按每立方米2.6元计费;当月用水量超过20立方米时,其中的20立方米仍按每立方米2.6元计费,超过部分按每立方米4元计费.设小刚家月用水量为x立方米.
(1)若小刚家4月份用水15立方米,则应收水费______元;当x超过20时,则应收水费_______元.
39
4x-28
综合练习
(2)小刚家6月份交水费62.4元,请你计算他家这个月的用水量.
解:因为2.6×20=52<62.4.
所以小刚家6月份的用水量超过20立方米.
根据题意得,
解得,x=22.6
答:小刚家6月份的用水量为22.6立方米.
课堂总结
一元一次方程
实际应用
步骤
类型
审、设、列、解、答
相关概念
相等关系
方程
方程的解
等式的性质
解一元一次方程
去分母、去括号、移项、合并同类项、系数化为1
配套问题、工程问题
球赛积分表问题
销售问题、方案问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
复习与小结
人教版七年级上册
第五章 一元一次方程
复习目标
重点
难点
从实际问题中抽象出数学模型.
理解配套问题、工程问题中的数量关系.
(1) 根据实际问题中数量关系列方程解决问题,并进一步熟练掌握一元一次方程的解法.
(2)培养数学建模能力,体会方程模型在实际问题求解过程中的优势.
知识框图
一元一次方程
实际应用
步骤
类型
审、设、列、解、答
相关概念
相等关系
方程
方程的解
等式的性质
解一元一次方程
去分母、去括号、移项、合并同类项、系数化为1
配套问题、工程问题
球赛积分表问题
销售问题、方案问题
知识梳理
知识点1 方程相关概念
(1)含有未知数的______叫做方程.
等式
(2)一般地,使方程左、右两边的值相等的______的值,叫做方程的解.
未知数
(3)一般地,如果方程中只含有_____个未知数(元),且含有未知数的式子都是_______,未知数的次数都是______,这样的方程叫做一元一次方程.
一
整式
1
知识梳理
1.下列各式中,属于方程的是( )
2.若x=2是方程4x+m=6的解,则m的值为_______.
3.已知关于x的方程 是一元一次方程,则a的值为_______.
D
-2
2
知识梳理
知识点2 等式的性质
等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
如果a=b,那么a±c=b±c.
等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc;
巩固提升
1.如果 ,那么根据等式的性质,下列变形错误的是( )
D
2.已知-4m+3=-4n+3,根据等式的性质,则m_____n.
=
知识梳理
知识点3 解一元一次方程
(1)解一元一次方程的一般步骤包括:______、去括号、______、合并同类项、__________.
去分母
移项
系数化为1
(2)去分母:一元一次方程中如果有分母,利用等式的性质_____,将方程的两边都乘各分母的__________,从而去掉分母.
2
最小公倍数
(3)移项:把等式一边的某项________移到另一边,叫做移项,其依据是___________.
变号后
等式的性质1
(4)系数化为1:利用等式的性质_____,将方程两边除以未知数的系数,将未知数的系数化为1.
2
巩固提升
1.解方程 ,以下去括号正确的是( )
B
2.已知代数式2+x和-x-6的值相等,则x的值为______.
-4
3.若多项式 互为相反数,则a的值为______.
-3
巩固提升
4.解下列方程.
解:
解:
知识梳理
知识点4 实际问题
(1)用一元一次方程解决实际问题的基本过程包括:设______、列方程、______、检验所得结果、确定答案.正确分析问题中的_______关系是列方程的基础.
未知数
解方程
相等
(2)配套问题中的基本相等关系:
若m个A物品与n个B物品配成一套,则_____×A数量=____×B的数量.
n
m
知识梳理
知识点4 实际问题
(3)工程问题中的基本相等关系:
工作量=________×工作时间.
工作效率
(4)销售问题中的基本相等关系:
售价=_____+进价=进价×(1+利润率)
利润=_____-进价.
利润
售价
利润率=(利润÷进价)×100%.
巩固提升
1. 某种商品因换季准备打折出售,如果按原定价的七五折出售,将赔25元,而按原定价的九折出售,将赚20元,则这种商品的原价是( )
A.500元 B.400元
C.300元 D.200元
D
巩固提升
2.某次数学竞赛共有20道题,已知做对一道得4分,做错一道或不做扣1分,某同学最后的得分是55分,则他做对了( )
A.16道 B.15道 C.14道 D.13道
3.一项工程由甲单独完成需要8天,由乙单独完成需要10天.现在由甲先做3天,剩下的甲乙合作完成.若设完成此项工程共需x天,可列方程为______________.
B
巩固提升
4.某车间有84名工人,平均每人每天加工16个大齿轮或10个小齿轮,已知1个大齿轮和2个小齿轮配套.为使每天加工的大、小齿轮刚好配套,应该每天安排多少名工人加工大齿轮?
解:设应该每天安排x名工人加工大齿轮,则(84-x)名工人加工小齿轮.
根据题意得:10(84-x)=2×16x
解得:x=20
所以,84-x=64
答:应该每天安排20名工人加工大齿轮.
综合练习
1.下列方程是一元一次方程的是( )
C
2.已知关于x的方程 的解是x=3,则k的值是( )
C
综合练习
3.下列方程变形正确的是( )
D
综合练习
4.阅读课上,语文老师将一些书分给各小组,若每个小组分8本,则剩余3本;若每个小组分9本,则缺少2本,问有几个小组?设有x个小组,可列方程为( )
B
综合练习
5.对于任意有理数a,b规定 ,若 ,则x的值为( )
A
综合练习
6.解下列方程.
解:
解:
综合练习
7.已知 与 都是关于x的一元一次方程,且有相同的解,求a的值.
解:
综合练习
8.一项工程,由甲单独做需要10天完成,乙单独做需要15天完成.若甲先做5天,再由甲乙合作,共完成全部工程的三分之二,则甲乙合作多少天?
解:设甲乙合作x天.
根据题意得,
解得,x= 1
答:甲乙合作1天.
综合练习
9.某服装店,打折销售服装,若每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元.每件服装的标价多少元?每件服装的成本价多少元?
解:设每件服装的标价为x元.
根据题意得,
解得,x=200
所以,0.5x+20=120
答:每件服装的标价为200元. 成本为120元.
综合练习
10.为鼓励居民节约用水,采用分段计费的方法收取水费:当月用水量不超过20立方米时,按每立方米2.6元计费;当月用水量超过20立方米时,其中的20立方米仍按每立方米2.6元计费,超过部分按每立方米4元计费.设小刚家月用水量为x立方米.
(1)若小刚家4月份用水15立方米,则应收水费______元;当x超过20时,则应收水费_______元.
39
4x-28
综合练习
(2)小刚家6月份交水费62.4元,请你计算他家这个月的用水量.
解:因为2.6×20=52<62.4.
所以小刚家6月份的用水量超过20立方米.
根据题意得,
解得,x=22.6
答:小刚家6月份的用水量为22.6立方米.
课堂总结
一元一次方程
实际应用
步骤
类型
审、设、列、解、答
相关概念
相等关系
方程
方程的解
等式的性质
解一元一次方程
去分母、去括号、移项、合并同类项、系数化为1
配套问题、工程问题
球赛积分表问题
销售问题、方案问题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
