第6讲 分式方程及其应用 讲义 -2025年中考数学一轮考点探究(广东)
文档属性
| 名称 | 第6讲 分式方程及其应用 讲义 -2025年中考数学一轮考点探究(广东) |
|
|
| 格式 | docx | ||
| 文件大小 | 94.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 20:46:55 | ||
图片预览



文档简介
第6讲 分式方程及其应用
(6年3考,4或7分)
【知识清单】
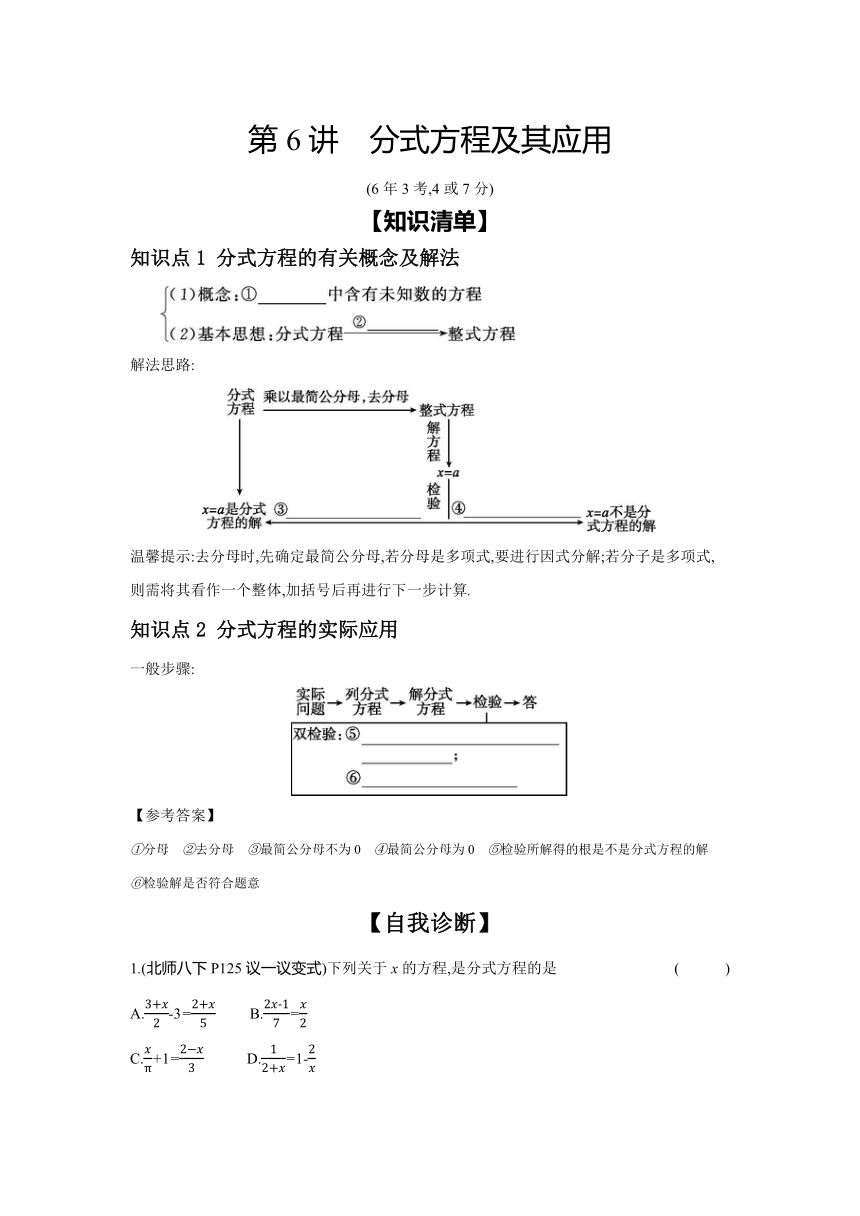
知识点1 分式方程的有关概念及解法
解法思路:
温馨提示:去分母时,先确定最简公分母,若分母是多项式,要进行因式分解;若分子是多项式,则需将其看作一个整体,加括号后再进行下一步计算.
知识点2 分式方程的实际应用
一般步骤:
【参考答案】
①分母 ②去分母 ③最简公分母不为0 ④最简公分母为0 ⑤检验所解得的根是不是分式方程的解 ⑥检验解是否符合题意
【自我诊断】
1.(北师八下P125议一议变式)下列关于x的方程,是分式方程的是 ( )
A.-3= B.=
C.+1= D.=1-
2.(人教八上P155第4题变式)数学家斐波那契编写的《算经》中有如下问题,一组人平分10元钱,每人分得若干;若再加上6人,平分40元钱,则第二次每人所得与第一次相同,求第二次分钱的人数.设第二次分钱的人数为x,则可列方程 ( )
A.10x=40(x+6) B.10(x-6)=40x
C.= D.=
3.(2023·广州一模)方程=的解为 .
4.(2021·衡阳)“绿水青山就是金山银山”.某地为美化环境,计划种植树木6000棵.由于志愿者的加入,实际每天植树的棵数比原计划增加了25%,结果提前3天完成任务.则实际每天植树 棵.
【参考答案】
1.D 2.D 3.x=2 4.500
【核心突破】
题型1 分式方程的解法
例题1 解方程:+1=.
方法总结
解分式方程注意事项:
1.去分母时,不要漏乘常数项;
2.去括号时,若括号前面是负号,则括号内每一项都要变号;
3.解得根后,要代入原分式方程或最简公分母中检验.
变式1 若关于x的分式方程=+1有增根,则m= .
2.解方程:=+1.
题型2 分式方程的应用
例题2 [真情境]某校团委开展以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品,到书店购买甲、乙两种书籍作为奖品.已知乙种书籍的单价是甲种书籍单价的1.25倍,用400元购买甲种书籍的数量比用同等金额购买乙种书籍的数量多4册.
(1)求甲、乙两种书籍的单价.
(2)团委决定用2000元购买甲、乙两种书籍共100册,此时,甲种书籍因改版售价比原价增加了20%,乙种书籍的售价按原价的七折出售.问最多能购买多少册甲种书籍
方法总结
分式方程应用题“双检验”:
在利用分式方程解决问题时,必须进行“双检验”:既要检验去分母化成的整式方程的解是否为原分式方程的解,又要检验分式方程的解是否符合实际意义.
变式2 2022年3月12日是第44个植树节,某街道办现计划采购樟树苗和柳树苗共600棵,已知一棵柳树苗比一棵樟树苗贵4元,用2400元所购买的樟树苗与用3200元所购买的柳树苗数量相同.
(1)请问一棵樟树苗的价格是多少元
(2)若购买樟树苗的数量不超过柳树苗的2倍,怎样采购所花费用最少 最少多少元
【参考答案】
例题1 【自主解答】+1=,
去分母,得2x-2+x2-1=x2+x,解得x=3,
检验:将x=3代入(x+1)(x-1)中,得(x+1)(x-1)≠0,∴x=3是该分式方程的解.
变式特训
1.3
【解析】去分母,得3x=m+3+(x-2),
整理,得2x=m+1.
∵关于x的分式方程=+1有增根,即x-2=0,∴x=2.
把x=2代入2x=m+1中,得2×2=m+1,解得m=3.
故答案为3.
2.【解析】=+1,
方程两边都乘(x-1)(x+1),得x(x+1)=4+(x-1)(x+1),解得x=3,
经检验,当x=3时,(x-1)(x+1)=8≠0.
故x=3是原方程的解.
例题2 【解析】(1)设甲种书籍的单价为x元,则乙种书籍的单价为1.25x元,由题意得-=4,
解得x=20,
经检验,x=20是原方程的解,且符合题意,
则1.25x=1.25×20=25.
答:甲种书籍的单价为20元,乙种书籍的单价为25元.
(2)设购买m册甲种书籍,则购买(100-m)册乙种书籍,由题意得(1+20%)×20m+25×0.7×(100-m)≤2000,解得m≤38.
∵m为正整数,∴m的最大值为38.
答:最多能购买38册甲种书籍.
变式特训 【解析】(1)设一棵樟树苗的价格是x元,则一棵柳树苗的价格为(x+4)元,
根据题意,得=,
解得x=12,
经检验,x=12是原分式方程的根,
∴一棵樟树苗的价格是12元.
(2)设购买m棵樟树苗,则购买了(600-m)棵柳树苗,总费用为w元,
根据题意,得m≤2(600-m),
解得m≤400,
w=12m+16(600-m)=-4m+9600.
∵-4<0,
∴w随着m的增大而减小,
∴当m=400时,w最小,
此时购买400棵樟树苗,200棵柳树苗,
最小花费w=-4×400+9600=8000(元).
【真题精粹】
考向1 解分式方程
真题拓展
1.下面是小明解方程-=1的过程,认真阅读并回答问题.
解:方程两边同时乘以最简公分母 ,
得(x-1)2-3=x2-1, 第一步
∴x2-2x+1-3=x2-1, 第二步
∴-2x=-1+3-1, 第三步
∴-2x=1, 第四步
∴x=-. 第五步
任务一:
①上述解题过程中,第一步的最简公分母是 ;
②上述第二步到第三步变形的依据是 .
任务二:上述解题过程是否完整,若不完整,请补充完整.
考向2 分式方程的应用(6年3考)
2.(2020·广东23题8分)某社区拟建A,B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米.建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元.用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的.
(1)问每个A,B类摊位占地面积各为多少平方米
(2)该社区拟建A,B两类摊位共90个,且B类摊位的数量不少于A类摊位数量的3倍.求建造这90个摊位的最大费用.
真题拓展
3.[真情境]红灯笼,象征着阖家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价.
(2)经市场调查发现,当乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对,物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.
①求y与x之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得的利润最大 最大利润是多少元
【参考答案】
1.【解析】任务一:①x2-1;
②等式的基本性质1:等式两边都加上(或都减去)同一个数或同一个式子,结果仍相等.
任务二:不完整,在第五步后补充如下内容:
检验:当x=-时,(x+1)(x-1)≠0,
所以,分式方程的解为x=-.
2.【解析】(1)设每个B类摊位的占地面积为x平方米,则每个A类摊位占地面积为(x+2)平方米,
根据题意得=×,
解得x=3,经检验x=3是原方程的解,
所以3+2=5.
答:每个A类摊位占地面积为5平方米,每个B类摊位的占地面积为3平方米.
(2)设建A类摊位a(a>0)个,则建B类摊位(90-a)个,
由题意得90-a≥3a,
解得a≤22.5.
∵建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,
∴要想使建造这90个摊位有最大费用,所以要多建造A类摊位,即当a取最大值22时,费用最大,此时最大费用为22×40×5+30×(90-22)×3=10520.
答:建造这90个摊位的最大费用是10520元.
3.【解析】(1)设甲种灯笼进价为n元/对,则乙种灯笼的进价为(n+9)元/对,由题意得=,
解得n=26,
经检验,n=26是原方程的解,且符合题意,
∴n+9=26+9=35.
答:甲种灯笼的进价为26元/对,乙种灯笼的进价为35元/对.
(2)①y=(50+x-35)(98-2x)=-2x2+68x+1470,
则y与x之间的函数解析式为y=-2x2+68x+1470.
②∵a=-2<0,
∴函数y有最大值,该二次函数的对称轴为x=-=17,∵物价部门规定其销售单价不高于每对65元,∴x+50≤65,∴x≤15.
∵当x<17时,y随x的增大而增大,
∴当x=15时,y最大=2040.
15+50=65.
答:乙种灯笼的销售单价为每对65元时,一天获得的利润最大,最大利润是2040元.
(6年3考,4或7分)
【知识清单】
知识点1 分式方程的有关概念及解法
解法思路:
温馨提示:去分母时,先确定最简公分母,若分母是多项式,要进行因式分解;若分子是多项式,则需将其看作一个整体,加括号后再进行下一步计算.
知识点2 分式方程的实际应用
一般步骤:
【参考答案】
①分母 ②去分母 ③最简公分母不为0 ④最简公分母为0 ⑤检验所解得的根是不是分式方程的解 ⑥检验解是否符合题意
【自我诊断】
1.(北师八下P125议一议变式)下列关于x的方程,是分式方程的是 ( )
A.-3= B.=
C.+1= D.=1-
2.(人教八上P155第4题变式)数学家斐波那契编写的《算经》中有如下问题,一组人平分10元钱,每人分得若干;若再加上6人,平分40元钱,则第二次每人所得与第一次相同,求第二次分钱的人数.设第二次分钱的人数为x,则可列方程 ( )
A.10x=40(x+6) B.10(x-6)=40x
C.= D.=
3.(2023·广州一模)方程=的解为 .
4.(2021·衡阳)“绿水青山就是金山银山”.某地为美化环境,计划种植树木6000棵.由于志愿者的加入,实际每天植树的棵数比原计划增加了25%,结果提前3天完成任务.则实际每天植树 棵.
【参考答案】
1.D 2.D 3.x=2 4.500
【核心突破】
题型1 分式方程的解法
例题1 解方程:+1=.
方法总结
解分式方程注意事项:
1.去分母时,不要漏乘常数项;
2.去括号时,若括号前面是负号,则括号内每一项都要变号;
3.解得根后,要代入原分式方程或最简公分母中检验.
变式1 若关于x的分式方程=+1有增根,则m= .
2.解方程:=+1.
题型2 分式方程的应用
例题2 [真情境]某校团委开展以感恩为主题的有奖征文活动,并为获奖的同学颁发奖品,到书店购买甲、乙两种书籍作为奖品.已知乙种书籍的单价是甲种书籍单价的1.25倍,用400元购买甲种书籍的数量比用同等金额购买乙种书籍的数量多4册.
(1)求甲、乙两种书籍的单价.
(2)团委决定用2000元购买甲、乙两种书籍共100册,此时,甲种书籍因改版售价比原价增加了20%,乙种书籍的售价按原价的七折出售.问最多能购买多少册甲种书籍
方法总结
分式方程应用题“双检验”:
在利用分式方程解决问题时,必须进行“双检验”:既要检验去分母化成的整式方程的解是否为原分式方程的解,又要检验分式方程的解是否符合实际意义.
变式2 2022年3月12日是第44个植树节,某街道办现计划采购樟树苗和柳树苗共600棵,已知一棵柳树苗比一棵樟树苗贵4元,用2400元所购买的樟树苗与用3200元所购买的柳树苗数量相同.
(1)请问一棵樟树苗的价格是多少元
(2)若购买樟树苗的数量不超过柳树苗的2倍,怎样采购所花费用最少 最少多少元
【参考答案】
例题1 【自主解答】+1=,
去分母,得2x-2+x2-1=x2+x,解得x=3,
检验:将x=3代入(x+1)(x-1)中,得(x+1)(x-1)≠0,∴x=3是该分式方程的解.
变式特训
1.3
【解析】去分母,得3x=m+3+(x-2),
整理,得2x=m+1.
∵关于x的分式方程=+1有增根,即x-2=0,∴x=2.
把x=2代入2x=m+1中,得2×2=m+1,解得m=3.
故答案为3.
2.【解析】=+1,
方程两边都乘(x-1)(x+1),得x(x+1)=4+(x-1)(x+1),解得x=3,
经检验,当x=3时,(x-1)(x+1)=8≠0.
故x=3是原方程的解.
例题2 【解析】(1)设甲种书籍的单价为x元,则乙种书籍的单价为1.25x元,由题意得-=4,
解得x=20,
经检验,x=20是原方程的解,且符合题意,
则1.25x=1.25×20=25.
答:甲种书籍的单价为20元,乙种书籍的单价为25元.
(2)设购买m册甲种书籍,则购买(100-m)册乙种书籍,由题意得(1+20%)×20m+25×0.7×(100-m)≤2000,解得m≤38.
∵m为正整数,∴m的最大值为38.
答:最多能购买38册甲种书籍.
变式特训 【解析】(1)设一棵樟树苗的价格是x元,则一棵柳树苗的价格为(x+4)元,
根据题意,得=,
解得x=12,
经检验,x=12是原分式方程的根,
∴一棵樟树苗的价格是12元.
(2)设购买m棵樟树苗,则购买了(600-m)棵柳树苗,总费用为w元,
根据题意,得m≤2(600-m),
解得m≤400,
w=12m+16(600-m)=-4m+9600.
∵-4<0,
∴w随着m的增大而减小,
∴当m=400时,w最小,
此时购买400棵樟树苗,200棵柳树苗,
最小花费w=-4×400+9600=8000(元).
【真题精粹】
考向1 解分式方程
真题拓展
1.下面是小明解方程-=1的过程,认真阅读并回答问题.
解:方程两边同时乘以最简公分母 ,
得(x-1)2-3=x2-1, 第一步
∴x2-2x+1-3=x2-1, 第二步
∴-2x=-1+3-1, 第三步
∴-2x=1, 第四步
∴x=-. 第五步
任务一:
①上述解题过程中,第一步的最简公分母是 ;
②上述第二步到第三步变形的依据是 .
任务二:上述解题过程是否完整,若不完整,请补充完整.
考向2 分式方程的应用(6年3考)
2.(2020·广东23题8分)某社区拟建A,B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米.建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元.用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的.
(1)问每个A,B类摊位占地面积各为多少平方米
(2)该社区拟建A,B两类摊位共90个,且B类摊位的数量不少于A类摊位数量的3倍.求建造这90个摊位的最大费用.
真题拓展
3.[真情境]红灯笼,象征着阖家团圆,红红火火,挂灯笼成为我国的一种传统文化.小明在春节前购进甲、乙两种红灯笼,用3120元购进甲灯笼与用4200元购进乙灯笼的数量相同,已知乙灯笼每对进价比甲灯笼每对进价多9元.
(1)求甲、乙两种灯笼每对的进价.
(2)经市场调查发现,当乙灯笼每对售价50元时,每天可售出98对,售价每提高1元,则每天少售出2对,物价部门规定其销售单价不高于每对65元,设乙灯笼每对涨价x元,小明一天通过乙灯笼获得利润y元.
①求y与x之间的函数解析式;
②乙种灯笼的销售单价为多少元时,一天获得的利润最大 最大利润是多少元
【参考答案】
1.【解析】任务一:①x2-1;
②等式的基本性质1:等式两边都加上(或都减去)同一个数或同一个式子,结果仍相等.
任务二:不完整,在第五步后补充如下内容:
检验:当x=-时,(x+1)(x-1)≠0,
所以,分式方程的解为x=-.
2.【解析】(1)设每个B类摊位的占地面积为x平方米,则每个A类摊位占地面积为(x+2)平方米,
根据题意得=×,
解得x=3,经检验x=3是原方程的解,
所以3+2=5.
答:每个A类摊位占地面积为5平方米,每个B类摊位的占地面积为3平方米.
(2)设建A类摊位a(a>0)个,则建B类摊位(90-a)个,
由题意得90-a≥3a,
解得a≤22.5.
∵建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,
∴要想使建造这90个摊位有最大费用,所以要多建造A类摊位,即当a取最大值22时,费用最大,此时最大费用为22×40×5+30×(90-22)×3=10520.
答:建造这90个摊位的最大费用是10520元.
3.【解析】(1)设甲种灯笼进价为n元/对,则乙种灯笼的进价为(n+9)元/对,由题意得=,
解得n=26,
经检验,n=26是原方程的解,且符合题意,
∴n+9=26+9=35.
答:甲种灯笼的进价为26元/对,乙种灯笼的进价为35元/对.
(2)①y=(50+x-35)(98-2x)=-2x2+68x+1470,
则y与x之间的函数解析式为y=-2x2+68x+1470.
②∵a=-2<0,
∴函数y有最大值,该二次函数的对称轴为x=-=17,∵物价部门规定其销售单价不高于每对65元,∴x+50≤65,∴x≤15.
∵当x<17时,y随x的增大而增大,
∴当x=15时,y最大=2040.
15+50=65.
答:乙种灯笼的销售单价为每对65元时,一天获得的利润最大,最大利润是2040元.
同课章节目录
