第9讲 平面直角坐标系与函数 讲义 -2025年中考数学一轮考点探究(广东)
文档属性
| 名称 | 第9讲 平面直角坐标系与函数 讲义 -2025年中考数学一轮考点探究(广东) | 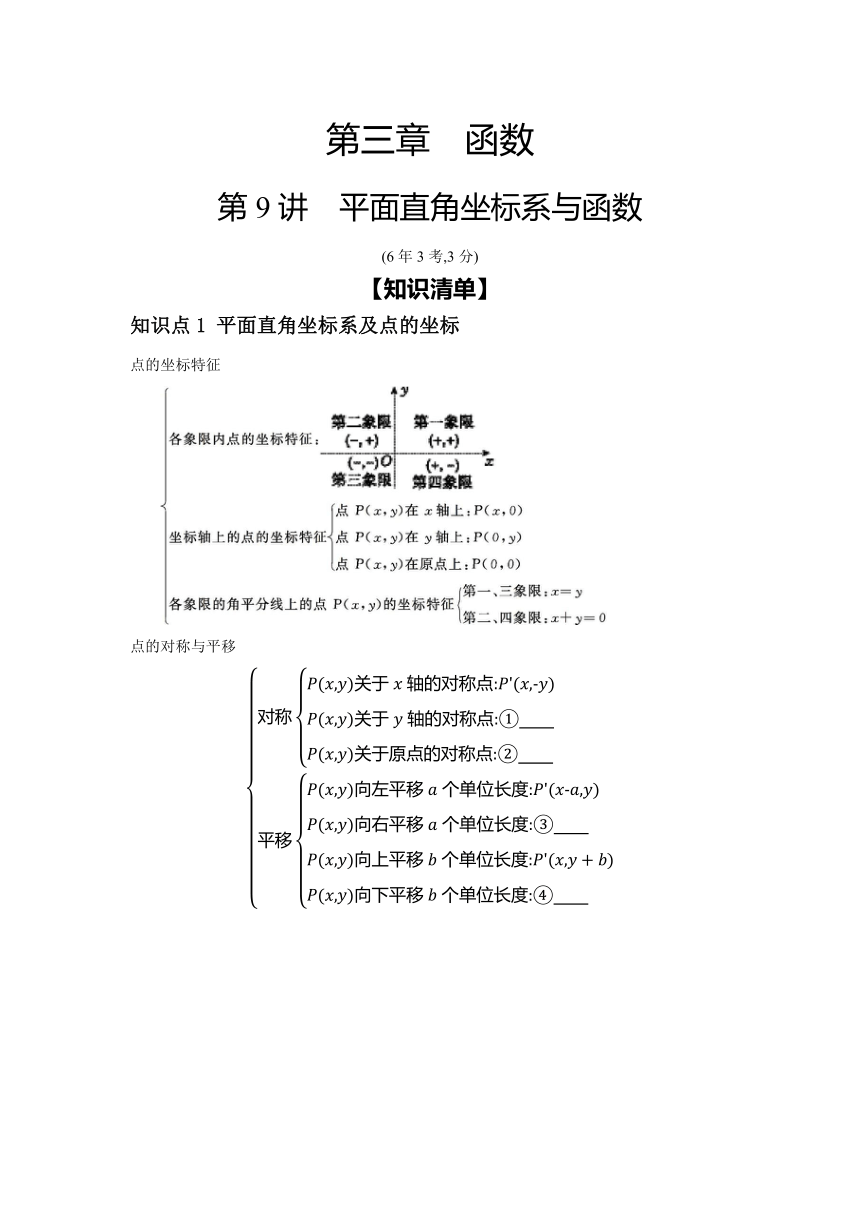 | |
| 格式 | docx | ||
| 文件大小 | 347.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 20:52:08 | ||
图片预览


文档简介
第三章 函数
第9讲 平面直角坐标系与函数
(6年3考,3分)
【知识清单】
知识点1 平面直角坐标系及点的坐标
点的坐标特征
点的对称与平移
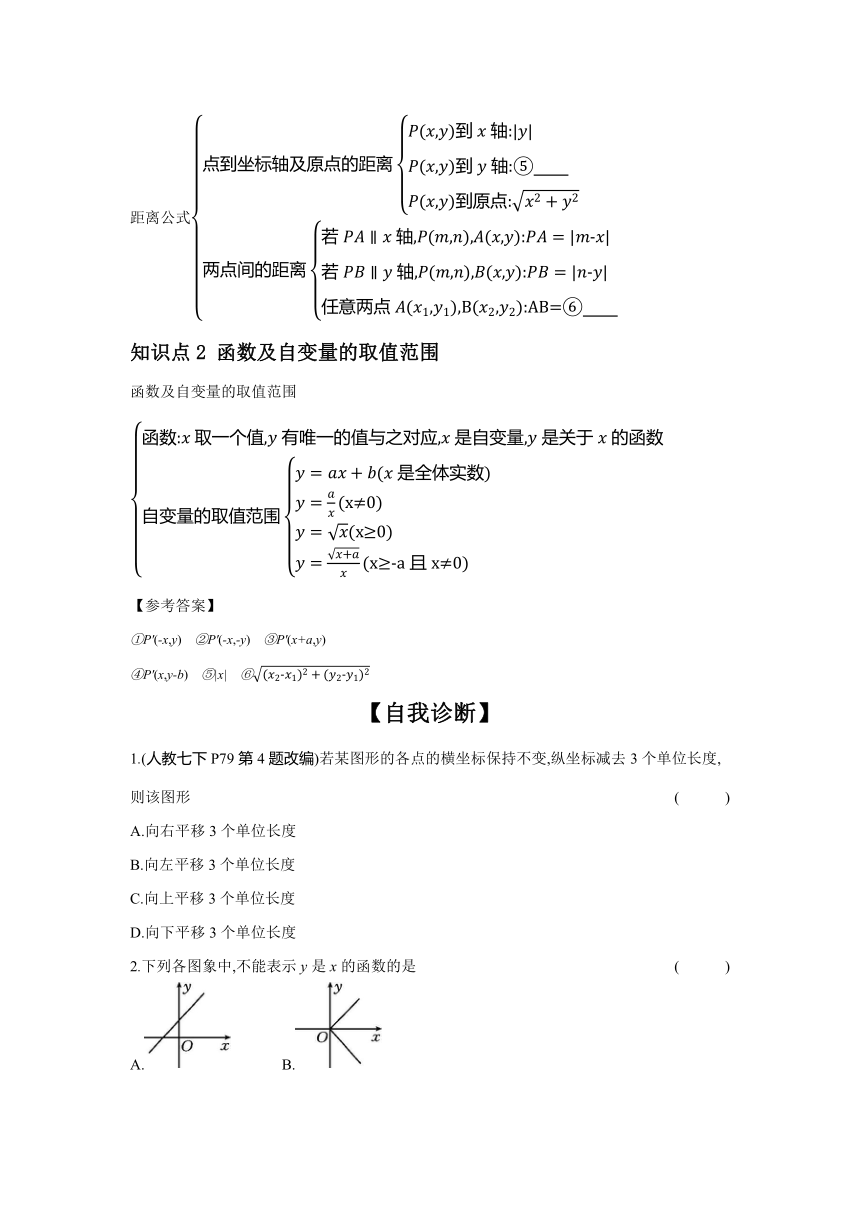
距离公式
知识点2 函数及自变量的取值范围
函数及自变量的取值范围
【参考答案】
①P'(-x,y) ②P'(-x,-y) ③P'(x+a,y)
④P'(x,y-b) ⑤|x| ⑥
【自我诊断】
1.(人教七下P79第4题改编)若某图形的各点的横坐标保持不变,纵坐标减去3个单位长度,则该图形 ( )
A.向右平移3个单位长度
B.向左平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
2.下列各图象中,不能表示y是x的函数的是 ( )
A. B.
C. D.
3.(北师八上P77第1题改编)台风给人们的出行带来很多不便,小明了解到去年8月16日的连续12个小时的风力变化情况,并画出了风力随时间变化的图象(如图),则下列说法正确的是 ( )
A.20时风力最小
B.8时风力最小
C.在8时至12时,风力最大为7级
D.8时至14时,风力不断增大
4.某人购进一批苹果到集贸市场零售,已知卖出的苹果数量x与销售额y的关系如下表:
数量x /千克 1 2 3 4 5
销售额y /元 3+0.1 6+0.2 9+0.3 12+0.4 15+0.5
则y与x之间的关系式为 .
【参考答案】1.D 2.B 3.A 4.y=3.1x
【核心突破】
题型1动点问题的函数图象
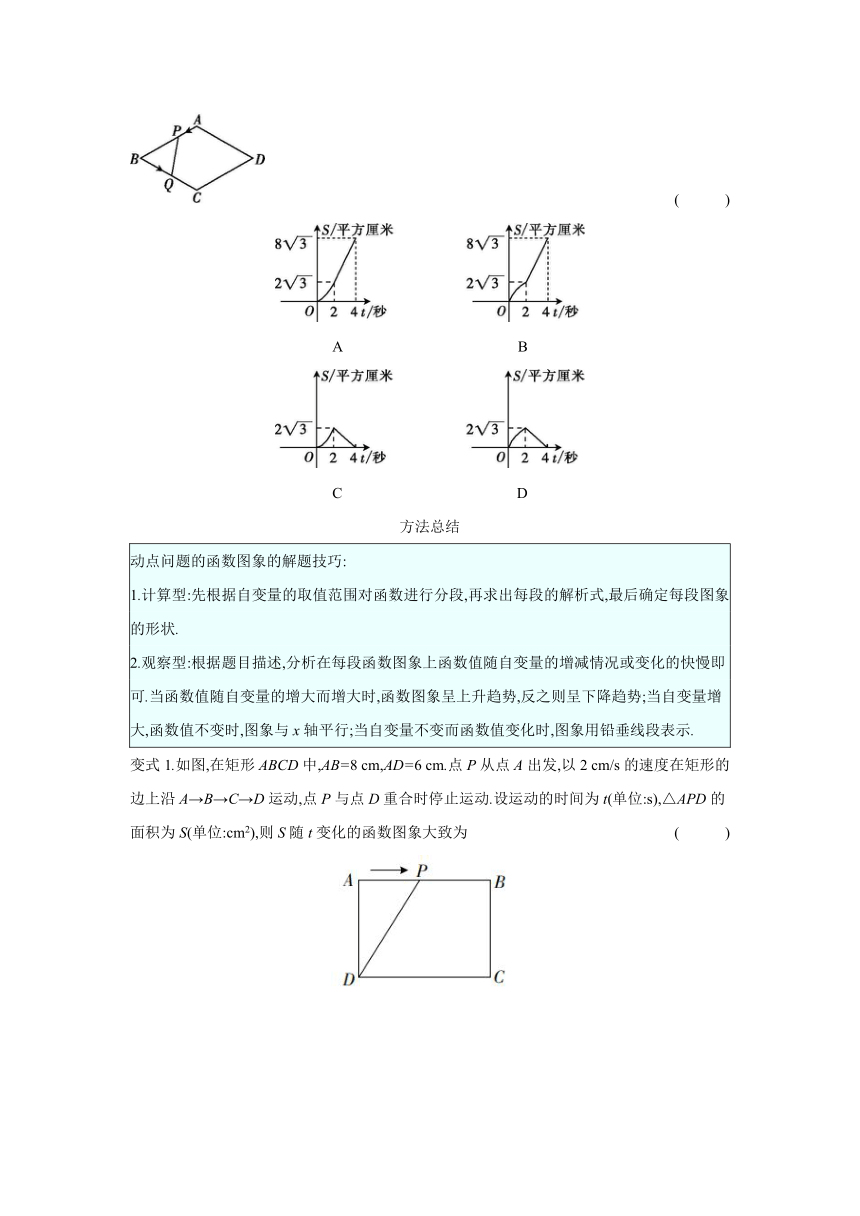
例题1如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米每秒的速度从点A出发沿AB方向运动至点B停止,动点Q以2厘米每秒的速度从点B出发沿折线BCD运动至点D停止.若点P,Q同时出发运动了t秒,记△BPQ的面积为S平方厘米,下列图象中能表示S与t之间的函数关系的是
( )
A B
C D
方法总结
动点问题的函数图象的解题技巧:
1.计算型:先根据自变量的取值范围对函数进行分段,再求出每段的解析式,最后确定每段图象的形状.
2.观察型:根据题目描述,分析在每段函数图象上函数值随自变量的增减情况或变化的快慢即可.当函数值随自变量的增大而增大时,函数图象呈上升趋势,反之则呈下降趋势;当自变量增大,函数值不变时,图象与x轴平行;当自变量不变而函数值变化时,图象用铅垂线段表示.
变式1.如图,在矩形ABCD中,AB=8 cm,AD=6 cm.点P从点A出发,以2 cm/s的速度在矩形的边上沿A→B→C→D运动,点P与点D重合时停止运动.设运动的时间为t(单位:s),△APD的面积为S(单位:cm2),则S随t变化的函数图象大致为 ( )
A B
C D
2.一对变量满足如图所示的函数关系.设计以下问题情境:
①阿明从家开车以600米/分的速度匀速开了2.5分钟,在原地停留了2分钟,然后以1000米/分的速度匀速开车回家.设所用时间为x分钟,离家的距离为y千米;
②有一个容积为1.5升的开口空瓶,小张以0.6升/秒的速度匀速向这个空瓶注水,注满后停止,等2秒后,再以1升/秒的速度匀速倒空瓶中的水.设所用时间为x秒,瓶内水的体积为y升;
③在矩形ABCD中,AB=2,BC=1.5,点P从点A出发.沿AC→CD→DA路线运动至点A停止.设点P的运动路程为x,△ABP的面积为y.
其中,符合图中函数关系的情境个数为 ( )
A.3 B.2 C.1 D.0
【参考答案】
例题 D
变式特训 1.D 2.A
【真题精粹】
考向1 平面直角坐标系中点的坐标特征(6年2考)
1.(2022·广东6题3分)在平面直角坐标系中,将点(1,1)向右平移2个单位长度后,得到的点的坐标是 ( )
A.(3,1) B.(-1,1)
C.(1,3) D.(1,-1)
2.(2020·广东3题3分)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 ( )
A.(-3,2) B.(-2,3)
C.(2,-3) D.(3,-2)
真题拓展
3.若点C在x轴的下方、y轴的右侧,距离x轴3个单位长度,距离y轴5个单位长度,则点C的坐标为 ( )
A.(-3,5) B.(3,-5)
C.(5,-3) D.(-5,3)
考向2 函数的有关概念(仅2022.T10考查)
4.(2022·广东10题3分)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr.下列判断正确的是 ( )
A.2是变量 B.π是变量 C.r是变量 D.C是常量
真题拓展
5.在函数y=中,自变量x的取值范围是 ( )
A.x>-3 B.x≥-3且x≠2
C.x≠2 D.x>-3且x≠2
考向3 动点问题的函数图象
(2018·广东10题3分)如图,P是菱形ABCD边上的一动点,它从点A出发,沿A→B→C→D的路径匀速运动到点D,设△PAD的面积为y,点P的运动时间为x,则y关于x的函数图象大致为
( )
A B
C D
真题拓展
如图,等边△ABC的边长为2 cm,点P从点A出发,以1 cm/s的速度向点C移动(到达点C后停止),同时点Q从点A出发,以1 cm/s的速度沿AB-BC的方向向点C移动(到达点C后停止),若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是
( )
A. B.
C. D.
8.如图1,在正方形ABCD中,E是边AD的中点,点P以1 cm/s的速度从点A出发,沿A→B→C运动到点C后,再沿线段CA到达点A.图2是点P运动时,△PEC的面积y( cm2)随时间x(s)变化的部分图象.根据图象判断,下列能表示点P在整个运动过程中,y随x变化的完整图象为 ( )
A B
C D
【参考答案】
1.A 2.D 3.C 4.C 5.B 6.B
7.C 【解析】当0≤t≤2时,S=·t·sin 60°t=t2,
此函数图象开口向上,且函数图象为抛物线右侧的一部分;
当2此函数图象是直线的一部分,且S随t的增大而减小,
所以符合题意的函数图象只有C.
故选C.
8.A 【解析】∵函数图象经过点(4,0),
∴AB+BC=1×4=4 cm,
∴AB=BC=CD=DA=2 cm.
∵E是边AD的中点,
∴DE=AE=1 cm.
当点P在AB上运动,即0AP=x cm,BP=(2-x)cm,
y=S正方形ABCD-S△ECD-S△AEP-S△PCB
=2×2-×1×2-×1·x-×2·(2-x)=x+1.
∵k=>0,∴y随x的增大而增大,
∴当x=2,即点P与点B重合时,y最大=2;
当点P在BC上运动时,
这时△PEC的高不变,底边CP越来越小,
∴△PEC的面积也越来越小,即y越来越小.
综上所述,当点P运动时,△PEC的面积的最大值是2,则y=2.由此可排除C,D.
当点P在CA上运动时,CP=(x-4)cm,如图,过点E作EM⊥AC于点M,则EM= cm,
∴y=×·(x-4)=x-,
由此可排除B.
故选A.
第9讲 平面直角坐标系与函数
(6年3考,3分)
【知识清单】
知识点1 平面直角坐标系及点的坐标
点的坐标特征
点的对称与平移
距离公式
知识点2 函数及自变量的取值范围
函数及自变量的取值范围
【参考答案】
①P'(-x,y) ②P'(-x,-y) ③P'(x+a,y)
④P'(x,y-b) ⑤|x| ⑥
【自我诊断】
1.(人教七下P79第4题改编)若某图形的各点的横坐标保持不变,纵坐标减去3个单位长度,则该图形 ( )
A.向右平移3个单位长度
B.向左平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
2.下列各图象中,不能表示y是x的函数的是 ( )
A. B.
C. D.
3.(北师八上P77第1题改编)台风给人们的出行带来很多不便,小明了解到去年8月16日的连续12个小时的风力变化情况,并画出了风力随时间变化的图象(如图),则下列说法正确的是 ( )
A.20时风力最小
B.8时风力最小
C.在8时至12时,风力最大为7级
D.8时至14时,风力不断增大
4.某人购进一批苹果到集贸市场零售,已知卖出的苹果数量x与销售额y的关系如下表:
数量x /千克 1 2 3 4 5
销售额y /元 3+0.1 6+0.2 9+0.3 12+0.4 15+0.5
则y与x之间的关系式为 .
【参考答案】1.D 2.B 3.A 4.y=3.1x
【核心突破】
题型1动点问题的函数图象
例题1如图,菱形ABCD的边长是4厘米,∠B=60°,动点P以1厘米每秒的速度从点A出发沿AB方向运动至点B停止,动点Q以2厘米每秒的速度从点B出发沿折线BCD运动至点D停止.若点P,Q同时出发运动了t秒,记△BPQ的面积为S平方厘米,下列图象中能表示S与t之间的函数关系的是
( )
A B
C D
方法总结
动点问题的函数图象的解题技巧:
1.计算型:先根据自变量的取值范围对函数进行分段,再求出每段的解析式,最后确定每段图象的形状.
2.观察型:根据题目描述,分析在每段函数图象上函数值随自变量的增减情况或变化的快慢即可.当函数值随自变量的增大而增大时,函数图象呈上升趋势,反之则呈下降趋势;当自变量增大,函数值不变时,图象与x轴平行;当自变量不变而函数值变化时,图象用铅垂线段表示.
变式1.如图,在矩形ABCD中,AB=8 cm,AD=6 cm.点P从点A出发,以2 cm/s的速度在矩形的边上沿A→B→C→D运动,点P与点D重合时停止运动.设运动的时间为t(单位:s),△APD的面积为S(单位:cm2),则S随t变化的函数图象大致为 ( )
A B
C D
2.一对变量满足如图所示的函数关系.设计以下问题情境:
①阿明从家开车以600米/分的速度匀速开了2.5分钟,在原地停留了2分钟,然后以1000米/分的速度匀速开车回家.设所用时间为x分钟,离家的距离为y千米;
②有一个容积为1.5升的开口空瓶,小张以0.6升/秒的速度匀速向这个空瓶注水,注满后停止,等2秒后,再以1升/秒的速度匀速倒空瓶中的水.设所用时间为x秒,瓶内水的体积为y升;
③在矩形ABCD中,AB=2,BC=1.5,点P从点A出发.沿AC→CD→DA路线运动至点A停止.设点P的运动路程为x,△ABP的面积为y.
其中,符合图中函数关系的情境个数为 ( )
A.3 B.2 C.1 D.0
【参考答案】
例题 D
变式特训 1.D 2.A
【真题精粹】
考向1 平面直角坐标系中点的坐标特征(6年2考)
1.(2022·广东6题3分)在平面直角坐标系中,将点(1,1)向右平移2个单位长度后,得到的点的坐标是 ( )
A.(3,1) B.(-1,1)
C.(1,3) D.(1,-1)
2.(2020·广东3题3分)在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 ( )
A.(-3,2) B.(-2,3)
C.(2,-3) D.(3,-2)
真题拓展
3.若点C在x轴的下方、y轴的右侧,距离x轴3个单位长度,距离y轴5个单位长度,则点C的坐标为 ( )
A.(-3,5) B.(3,-5)
C.(5,-3) D.(-5,3)
考向2 函数的有关概念(仅2022.T10考查)
4.(2022·广东10题3分)水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为C=2πr.下列判断正确的是 ( )
A.2是变量 B.π是变量 C.r是变量 D.C是常量
真题拓展
5.在函数y=中,自变量x的取值范围是 ( )
A.x>-3 B.x≥-3且x≠2
C.x≠2 D.x>-3且x≠2
考向3 动点问题的函数图象
(2018·广东10题3分)如图,P是菱形ABCD边上的一动点,它从点A出发,沿A→B→C→D的路径匀速运动到点D,设△PAD的面积为y,点P的运动时间为x,则y关于x的函数图象大致为
( )
A B
C D
真题拓展
如图,等边△ABC的边长为2 cm,点P从点A出发,以1 cm/s的速度向点C移动(到达点C后停止),同时点Q从点A出发,以1 cm/s的速度沿AB-BC的方向向点C移动(到达点C后停止),若△APQ的面积为S(cm2),则下列最能反映S(cm2)与移动时间t(s)之间函数关系的大致图象是
( )
A. B.
C. D.
8.如图1,在正方形ABCD中,E是边AD的中点,点P以1 cm/s的速度从点A出发,沿A→B→C运动到点C后,再沿线段CA到达点A.图2是点P运动时,△PEC的面积y( cm2)随时间x(s)变化的部分图象.根据图象判断,下列能表示点P在整个运动过程中,y随x变化的完整图象为 ( )
A B
C D
【参考答案】
1.A 2.D 3.C 4.C 5.B 6.B
7.C 【解析】当0≤t≤2时,S=·t·sin 60°t=t2,
此函数图象开口向上,且函数图象为抛物线右侧的一部分;
当2
所以符合题意的函数图象只有C.
故选C.
8.A 【解析】∵函数图象经过点(4,0),
∴AB+BC=1×4=4 cm,
∴AB=BC=CD=DA=2 cm.
∵E是边AD的中点,
∴DE=AE=1 cm.
当点P在AB上运动,即0
y=S正方形ABCD-S△ECD-S△AEP-S△PCB
=2×2-×1×2-×1·x-×2·(2-x)=x+1.
∵k=>0,∴y随x的增大而增大,
∴当x=2,即点P与点B重合时,y最大=2;
当点P在BC上运动时,
这时△PEC的高不变,底边CP越来越小,
∴△PEC的面积也越来越小,即y越来越小.
综上所述,当点P运动时,△PEC的面积的最大值是2,则y=2.由此可排除C,D.
当点P在CA上运动时,CP=(x-4)cm,如图,过点E作EM⊥AC于点M,则EM= cm,
∴y=×·(x-4)=x-,
由此可排除B.
故选A.
同课章节目录
