第10讲 一次函数的图象与性质 讲义 -2025年中考数学一轮考点探究(广东)
文档属性
| 名称 | 第10讲 一次函数的图象与性质 讲义 -2025年中考数学一轮考点探究(广东) |
|
|
| 格式 | docx | ||
| 文件大小 | 133.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 00:00:00 | ||
图片预览



文档简介
第10讲 一次函数的图象与性质
(6年5考,2~4分)
【知识清单】
知识点1 一次函数、正比例函数
一次函数、正比例函数
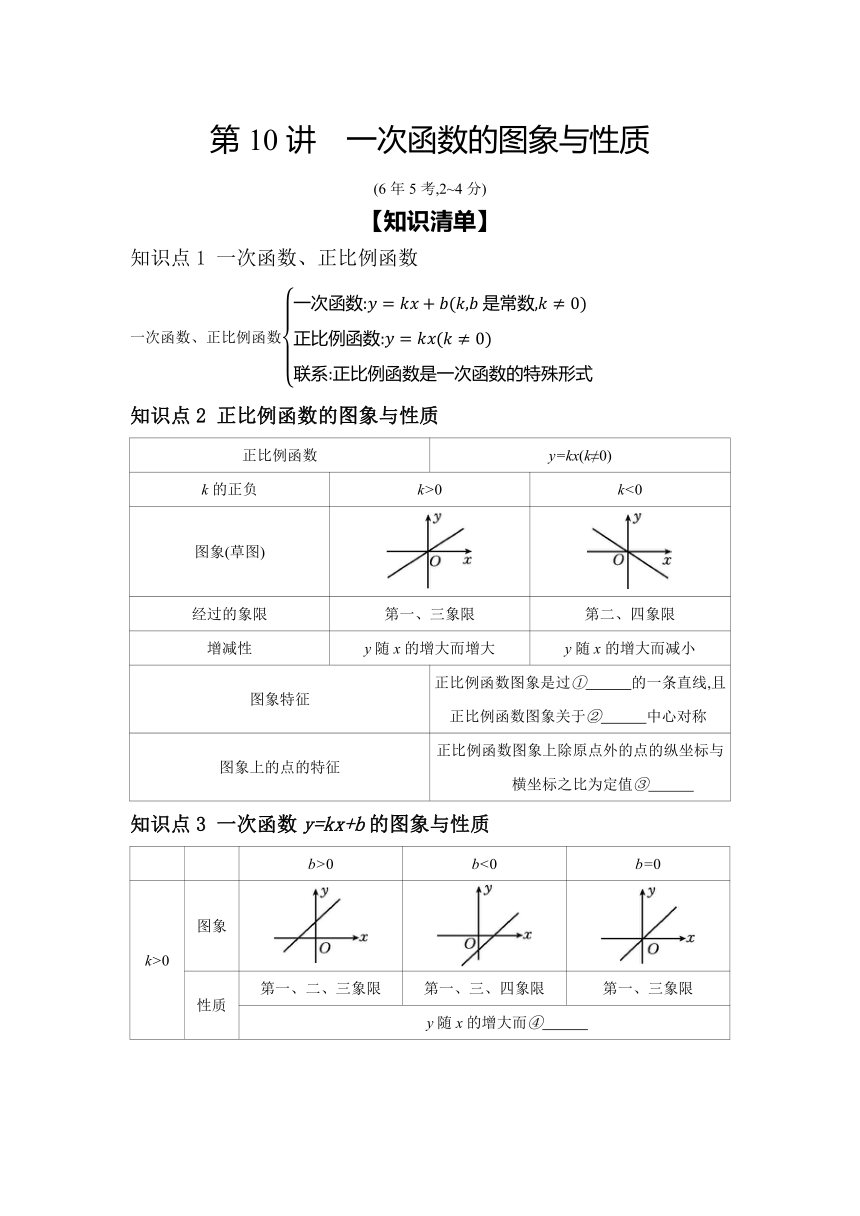
知识点2 正比例函数的图象与性质
正比例函数 y=kx(k≠0)
k的正负 k>0 k<0
图象(草图)
经过的象限 第一、三象限 第二、四象限
增减性 y随x的增大而增大 y随x的增大而减小
图象特征 正比例函数图象是过① 的一条直线,且正比例函数图象关于② 中心对称
图象上的点的特征 正比例函数图象上除原点外的点的纵坐标与横坐标之比为定值③
知识点3 一次函数y=kx+b的图象与性质
b>0 b<0 b=0
k>0 图象
性质 第一、二、三象限 第一、三、四象限 第一、三象限
y随x的增大而④
k<0 图象
性质 第一、二、四象限 第二、三、四象限 第二、四象限
y随x的增大而⑤
图象关系 一次函数y=kx+b(k≠0)的图象可由正比例函数y=kx(k≠0)的图象平移得到,若b>0,则向上平移b个单位长度;若b<0,则向下平移|b|个单位长度
知识点4 一次函数解析式的确定
一次函数解析式的确定
知识点5 一次函数与方程、不等式的关系
一次函数
【参考答案】
①原点 ②原点 ③k ④增大 ⑤减小
【自我诊断】
1.下列函数中,属于正比例函数的是 ( )
A.y=x2+2 B.y=-2x+1
C.y= D.y=
2.一次函数y=kx+b的图象如图所示,则k,b满足的条件为 ( )
A.k<0,b>0 B.k<0,b<0
C.k>0,b<0 D.k>0,b>0
3.如果直线y=kx+b(k≠0)经过A(0,2)和B(3,0)两点,那么这个一次函数的解析式是 ( )
A.y=2x+3 B.y=-x+2
C.y=3x+2 D.y=x+1
4.一次函数y=ax+b的图象如图所示,则关于x的一元一次方程ax+b=-1的解是 ( )
A.x=-2 B.x=-1
C.x=2 D.x=0
【参考答案】
1.D 2.C 3.B 4.D
【核心突破】
题型1 求一次函数的解析式
例题1 如图,在平面直角坐标系中,直线l1:y=-x+3与过点A(-3,0)的直线l2交于点P(-1,m),与x轴交于点B.
(1)求直线l2的函数解析式.
(2)点M在直线l2上,MN∥y轴,交直线l1于点N,若MN=AB,求点M的坐标.
方法总结
运用待定系数法求一次函数解析式的步骤:
(1)设:设出一次函数解析式:y=kx+b(k≠0).
(2)代:把已知条件代入解析式得到关于k和b的二元一次方程组.
(3)解:解方程组,求出k,b的值.
(4)回代:将求出的k,b的值代入所设函数解析式,即可得到所求的一次函数解析式.
变式1 如图,在平面直角坐标系中,直线l1:y=x+6与y轴交于点A,直线l2:y=kx+b与y轴交于点B,与l1交于点C(-3,3),AO=2BO.
(1)求直线l2:y=kx+b的解析式.
(2)求△ABC的面积.
【参考答案】
例题 【自主解答】(1)∵直线l1:y=-x+3与直线l2交于点P(-1,m),
∴m=-(-1)+3=4,即P(-1,4).
又∵l2过点A(-3,0)和点P(-1,4),
设直线l2的函数解析式为y=kx+b,
∴
解得
∴直线l2的函数解析式为y=2x+6.
(2)在y=-x+3中,令y=0,得x=3,
∴B(3,0),∴AB=3-(-3)=6.
设M(a,2a+6),由MN∥y轴,得N(a,-a+3),
则MN=|(2a+6)-(-a+3)|=AB=6,
即3a+3=6或3a+3=-6,解得a=1或a=-3,
∴M(1,8)或M(-3,0).
变式特训 【解析】(1)∵直线l1:y=x+6与y轴交于点A,
∴当x=0时,y=0+6=6,∴A(0,6).
∵AO=2BO,∴B(0,-3).
把C(-3,3)代入直线l2:y=kx+b,
得解得
故直线l2的解析式为y=-2x-3.
(2)S△ABC=AB·|xc|=×(6+3)×3=.
【真题精粹】
考向1 一次函数的图象与性质
真题拓展
1.(2023·广州一模)点(3,-3)在正比例函数y=ax(a≠0)的图象上,则a的值为 ( )
A.-2 B.- C.-1 D.-
2.下列关于一次函数y=3x-3的性质的说法不正确的是 ( )
A.不经过第二象限
B.与y轴交于点(0,-3)
C.与x轴交于点(-1,0)
D.y随x的增大而增大
3.在平面直角坐标系中,若点A(-a,b)在第三象限,则函数y=ax+b的图象大致是 ( )
A B
C D
4.(2023·新疆)一次函数y=x+1的图象不经过 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
考向2 求一次函数的表达式
5.将直线y=-6x向下平移2个单位长度,平移后直线的解析式为 .
6.(2023·广东16(2)题5分)已知一次函数y=kx+b的图象经过点(0,1)与点(2,5),求该一次函数的表达式.
考向3 一次函数与方程(组)、不等式的关系
真题拓展
如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是 ( )
A.x= B.x=1 C.x=2 D.x=4
8.如图,函数y=kx+b(k≠0)的图象经过点B(m,0)(m>1),与函数y=2x的图象交于点A,则不等式kx+b<2x的解集为 ( )
A.x>0 B.x<1 C.x>1 D.x>2
9.如图,已知函数y=2x+b的图象与函数y=kx-3的图象交于点P,则方程组的解是 .
【参考答案】
1.C 2.C 3.C 4.D 5.y=-6x-2
6.【解析】将(0,1)与(2,5)代入y=kx+b,
得
解得
∴该一次函数的表达式为y=2x+1.
7.B 8.C 9.
(6年5考,2~4分)
【知识清单】
知识点1 一次函数、正比例函数
一次函数、正比例函数
知识点2 正比例函数的图象与性质
正比例函数 y=kx(k≠0)
k的正负 k>0 k<0
图象(草图)
经过的象限 第一、三象限 第二、四象限
增减性 y随x的增大而增大 y随x的增大而减小
图象特征 正比例函数图象是过① 的一条直线,且正比例函数图象关于② 中心对称
图象上的点的特征 正比例函数图象上除原点外的点的纵坐标与横坐标之比为定值③
知识点3 一次函数y=kx+b的图象与性质
b>0 b<0 b=0
k>0 图象
性质 第一、二、三象限 第一、三、四象限 第一、三象限
y随x的增大而④
k<0 图象
性质 第一、二、四象限 第二、三、四象限 第二、四象限
y随x的增大而⑤
图象关系 一次函数y=kx+b(k≠0)的图象可由正比例函数y=kx(k≠0)的图象平移得到,若b>0,则向上平移b个单位长度;若b<0,则向下平移|b|个单位长度
知识点4 一次函数解析式的确定
一次函数解析式的确定
知识点5 一次函数与方程、不等式的关系
一次函数
【参考答案】
①原点 ②原点 ③k ④增大 ⑤减小
【自我诊断】
1.下列函数中,属于正比例函数的是 ( )
A.y=x2+2 B.y=-2x+1
C.y= D.y=
2.一次函数y=kx+b的图象如图所示,则k,b满足的条件为 ( )
A.k<0,b>0 B.k<0,b<0
C.k>0,b<0 D.k>0,b>0
3.如果直线y=kx+b(k≠0)经过A(0,2)和B(3,0)两点,那么这个一次函数的解析式是 ( )
A.y=2x+3 B.y=-x+2
C.y=3x+2 D.y=x+1
4.一次函数y=ax+b的图象如图所示,则关于x的一元一次方程ax+b=-1的解是 ( )
A.x=-2 B.x=-1
C.x=2 D.x=0
【参考答案】
1.D 2.C 3.B 4.D
【核心突破】
题型1 求一次函数的解析式
例题1 如图,在平面直角坐标系中,直线l1:y=-x+3与过点A(-3,0)的直线l2交于点P(-1,m),与x轴交于点B.
(1)求直线l2的函数解析式.
(2)点M在直线l2上,MN∥y轴,交直线l1于点N,若MN=AB,求点M的坐标.
方法总结
运用待定系数法求一次函数解析式的步骤:
(1)设:设出一次函数解析式:y=kx+b(k≠0).
(2)代:把已知条件代入解析式得到关于k和b的二元一次方程组.
(3)解:解方程组,求出k,b的值.
(4)回代:将求出的k,b的值代入所设函数解析式,即可得到所求的一次函数解析式.
变式1 如图,在平面直角坐标系中,直线l1:y=x+6与y轴交于点A,直线l2:y=kx+b与y轴交于点B,与l1交于点C(-3,3),AO=2BO.
(1)求直线l2:y=kx+b的解析式.
(2)求△ABC的面积.
【参考答案】
例题 【自主解答】(1)∵直线l1:y=-x+3与直线l2交于点P(-1,m),
∴m=-(-1)+3=4,即P(-1,4).
又∵l2过点A(-3,0)和点P(-1,4),
设直线l2的函数解析式为y=kx+b,
∴
解得
∴直线l2的函数解析式为y=2x+6.
(2)在y=-x+3中,令y=0,得x=3,
∴B(3,0),∴AB=3-(-3)=6.
设M(a,2a+6),由MN∥y轴,得N(a,-a+3),
则MN=|(2a+6)-(-a+3)|=AB=6,
即3a+3=6或3a+3=-6,解得a=1或a=-3,
∴M(1,8)或M(-3,0).
变式特训 【解析】(1)∵直线l1:y=x+6与y轴交于点A,
∴当x=0时,y=0+6=6,∴A(0,6).
∵AO=2BO,∴B(0,-3).
把C(-3,3)代入直线l2:y=kx+b,
得解得
故直线l2的解析式为y=-2x-3.
(2)S△ABC=AB·|xc|=×(6+3)×3=.
【真题精粹】
考向1 一次函数的图象与性质
真题拓展
1.(2023·广州一模)点(3,-3)在正比例函数y=ax(a≠0)的图象上,则a的值为 ( )
A.-2 B.- C.-1 D.-
2.下列关于一次函数y=3x-3的性质的说法不正确的是 ( )
A.不经过第二象限
B.与y轴交于点(0,-3)
C.与x轴交于点(-1,0)
D.y随x的增大而增大
3.在平面直角坐标系中,若点A(-a,b)在第三象限,则函数y=ax+b的图象大致是 ( )
A B
C D
4.(2023·新疆)一次函数y=x+1的图象不经过 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
考向2 求一次函数的表达式
5.将直线y=-6x向下平移2个单位长度,平移后直线的解析式为 .
6.(2023·广东16(2)题5分)已知一次函数y=kx+b的图象经过点(0,1)与点(2,5),求该一次函数的表达式.
考向3 一次函数与方程(组)、不等式的关系
真题拓展
如图,直线y=2x与y=kx+b相交于点P(m,2),则关于x的方程kx+b=2的解是 ( )
A.x= B.x=1 C.x=2 D.x=4
8.如图,函数y=kx+b(k≠0)的图象经过点B(m,0)(m>1),与函数y=2x的图象交于点A,则不等式kx+b<2x的解集为 ( )
A.x>0 B.x<1 C.x>1 D.x>2
9.如图,已知函数y=2x+b的图象与函数y=kx-3的图象交于点P,则方程组的解是 .
【参考答案】
1.C 2.C 3.C 4.D 5.y=-6x-2
6.【解析】将(0,1)与(2,5)代入y=kx+b,
得
解得
∴该一次函数的表达式为y=2x+1.
7.B 8.C 9.
同课章节目录
