14.2.1勾股定理的应用(最短路径问题) 课件(共28张PPT)
文档属性
| 名称 | 14.2.1勾股定理的应用(最短路径问题) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
数学家名言分享
树老易空,人老易松,科学之道,戒之以空,戒之以松,我愿一辈子从实而终。
——华罗庚
请拿出你的课本、彩色笔和练习本等用品,还有你的激情和坐姿。
华师大版 八年级 上册
01
勾股定理的应用——最短路径问题
复习提问:
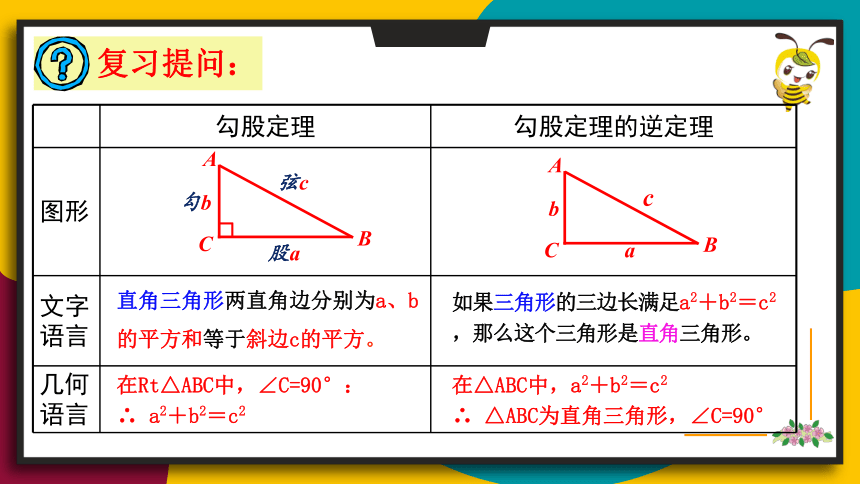
勾股定理 勾股定理的逆定理
图形
文字语言
几何语言
A
勾b
股a
C
B
∟
弦c
直角三角形两直角边分别为a、b的平方和等于斜边c的平方。
在Rt△ABC中,∠C=90°:
∴ a2+b2=c2
A
b
a
C
B
c
如果三角形的三边长满足a2+b2=c2,那么这个三角形是直角三角形。
在△ABC中,a2+b2=c2
∴ △ABC为直角三角形,∠C=90°
复习提问:
一、判断题:
1、在△ABC中:AB=5,AC=12,则BC=13 ( )
2、直角三角形ABC中:a=6,b=8,则c=10 ( )
二、填空题:
3、能与3和4围成三角形的数有 个;能与3和4围成直角三角形的有 个;能与3和4组成勾股数的数有 个。
4、三角形三边分别为6、8、10,那么最短边上的高为 ,最长边上的高为 。
×
两边之差<BC<两边之和 即:7<BC<17
√
无数
两
1
8
4.8
1、直角三角形斜边上的高等于两直角边之积除以斜边。
2、构造方程:S△=0.5ab=0.5ch
前提:Rt△
情境导入
情境导入
学会用数学的眼光观察事物
1
情景探究一
在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
AC+CB>AB(两点之间线段最短)
B
A
3米
4米
C
2
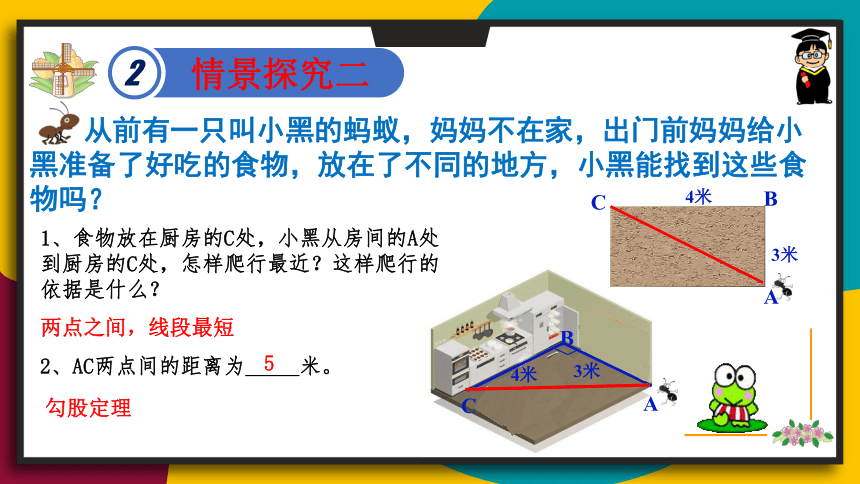
情景探究二
从前有一只叫小黑的蚂蚁,妈妈不在家,出门前妈妈给小黑准备了好吃的食物,放在了不同的地方,小黑能找到这些食物吗?
2、AC两点间的距离为 米。
1、食物放在厨房的C处,小黑从房间的A处到厨房的C处,怎样爬行最近?这样爬行的依据是什么?
A
4米
3米
B
C
两点之间,线段最短
5
勾股定理
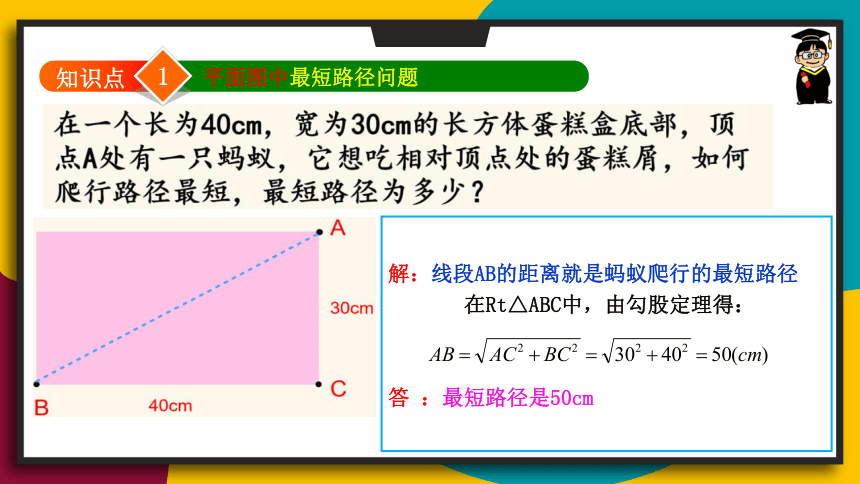
解:线段AB的距离就是蚂蚁爬行的最短路径
在Rt△ABC中,由勾股定理得:
答 :最短路径是50cm
1
平面图中最短路径问题
知识点
这个问题研究的过程是怎么的呢?
实际问题
两点之间,线段最短或垂线段最短
数学问题
勾股定理
立体图形又如何解决呢
1
平面图中最短路径问题
知识点
2
立体图形圆柱最短路径问题
知识点
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径。一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程。(结果保留根号)
2
立体图形圆柱最短路径问题
知识点
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径。一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程。(结果保留根号)
A
B
C
D
解:如图所示,由题意可知:
BC=底面周长的一半=10cm,AB=4cm
在Rt△ABC中,由勾股定理得:
答:爬行的最短路程约为 cm。
o
变式:一只蚂蚁从点A出发,沿着圆柱的侧面爬行到CD的中点O,已知底面周长为10,试求出爬行的最短路程。
A
A
B
D
C
4
3
O
解:如图,由题意可知:
OD=4÷2=2,AD=10÷2=5。
在Rt△ABO中,由勾股定理得:
答:最短路程为 厘米。
3
立体图形正方体最短路径问题
知识点
如图,桌子上有一个边长为10cm且无盖的正方体型盒子,底面不可通行,若妈妈把食物放在正方体的C处,小黑蚂蚁从A点出发,沿着正方体的外表面爬行,则最短的路径的长是多少cm。
A
C
B
解:在Rt△ABC中,由勾股定理得:
AC=
经过前面和右面
3
立体图形正方体最短路径问题
知识点
如图,桌子上有一个边长为10cm且无盖的正方体型盒子,底面不可通行,若妈妈把食物放在正方体的C处,小黑蚂蚁从A点出发,沿着正方体的外表面爬行,则最短的路径的长是多少cm。
A
C
B
解:在Rt△ABC中,由勾股定理得:
AC=
经过左面和后面
提炼方法——
1、将立体图形展开,转化成平面图形。
2、在平面图中找到对应的起点和终点,即对应点位置。
3、在平面图形中,连接起点和终点,得出线段。
解:在Rt△ABC中,由勾股定理得:
4、构建直角三角形,利用勾股定理求出线段的长度,比较,得最短路径。
5、答题。
展
找
连
求
答
归纳总结:立体图形表面最短路径问题
方法:
立体图形
平面图形
直角三角形
建模
转化分类讨论
勾股定理
两点之间,线段最短
展
找
连
求
答
本节课数学思想
化归转化思想
4
立体图形长方体最短路径问题
知识点
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
分析:蚂蚁由A爬到C1过程中较短的路线有多少种情况?
①经过前面和右面
②经过前面和上面
③经过左面和上面
①经过前面和右面
②经过前面和上面
③经过左面和上面
解:(1)当蚂蚁经过前面和右面时,最短路程为:
(2)当蚂蚁经过前面和上面时,最短路程为:
(3)当蚂蚁经过左面和上面时,最短路程为:
∴ 最短路程为 ㎝。
拓展提高:如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm、3cm、1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
A
B
C
D
解: 由题意可知:AC=5, BC=3×3+3×1=12
在Rt△ABC中,由勾股定理得:
答:从A点爬到B点,最短线路是13cm。
A
B
C
D
应用勾股定理解决实际问题的一般思路:
1、立体图形中路线最短的问题,往往是把立体图形展开,得到平面图形。根据“两点之间,线段最短” 确定行走路线,根据勾股定理计算出最短距离。
2、在解决实际问题时,首先要画出适当的示意图,将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题。
提炼方法——
立体图形
平面图形
直角三角形
建模
转化
勾股定理
两点之间,线段最短
化归转化思想
知识点
最短路径问题
本节课的数学思想
1.本节课学习了哪些知识?用了什么数学思想方法?
2.你们有什么收获?
总结反思
示例 长方体表面上A,B两点间的最短距离
作 业
练习册
谢谢欣赏
THANK YOU FOR LISTENING
如图,一个无盖长方形盒子的长、宽、高分别是4cm、4cm、6cm,一只蚂蚁想从盒底的A点沿盒的表面爬到盒顶的B点,蚂蚁要爬的最短路程是( )
A. 5cm B. 8cm C. 10cm D.7cm
解:长方体展开,将长方体展开,进而得出最短路线。
可得:AB2=62+82=100
∴AB=10(cm)
故最短路程为10cm。
C
B
A
A
B
6
4
4
练习1
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
数学家名言分享
树老易空,人老易松,科学之道,戒之以空,戒之以松,我愿一辈子从实而终。
——华罗庚
请拿出你的课本、彩色笔和练习本等用品,还有你的激情和坐姿。
华师大版 八年级 上册
01
勾股定理的应用——最短路径问题
复习提问:
勾股定理 勾股定理的逆定理
图形
文字语言
几何语言
A
勾b
股a
C
B
∟
弦c
直角三角形两直角边分别为a、b的平方和等于斜边c的平方。
在Rt△ABC中,∠C=90°:
∴ a2+b2=c2
A
b
a
C
B
c
如果三角形的三边长满足a2+b2=c2,那么这个三角形是直角三角形。
在△ABC中,a2+b2=c2
∴ △ABC为直角三角形,∠C=90°
复习提问:
一、判断题:
1、在△ABC中:AB=5,AC=12,则BC=13 ( )
2、直角三角形ABC中:a=6,b=8,则c=10 ( )
二、填空题:
3、能与3和4围成三角形的数有 个;能与3和4围成直角三角形的有 个;能与3和4组成勾股数的数有 个。
4、三角形三边分别为6、8、10,那么最短边上的高为 ,最长边上的高为 。
×
两边之差<BC<两边之和 即:7<BC<17
√
无数
两
1
8
4.8
1、直角三角形斜边上的高等于两直角边之积除以斜边。
2、构造方程:S△=0.5ab=0.5ch
前提:Rt△
情境导入
情境导入
学会用数学的眼光观察事物
1
情景探究一
在A点的小狗,为了尽快吃到B点的香肠,它选择A B 路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
AC+CB>AB(两点之间线段最短)
B
A
3米
4米
C
2
情景探究二
从前有一只叫小黑的蚂蚁,妈妈不在家,出门前妈妈给小黑准备了好吃的食物,放在了不同的地方,小黑能找到这些食物吗?
2、AC两点间的距离为 米。
1、食物放在厨房的C处,小黑从房间的A处到厨房的C处,怎样爬行最近?这样爬行的依据是什么?
A
4米
3米
B
C
两点之间,线段最短
5
勾股定理
解:线段AB的距离就是蚂蚁爬行的最短路径
在Rt△ABC中,由勾股定理得:
答 :最短路径是50cm
1
平面图中最短路径问题
知识点
这个问题研究的过程是怎么的呢?
实际问题
两点之间,线段最短或垂线段最短
数学问题
勾股定理
立体图形又如何解决呢
1
平面图中最短路径问题
知识点
2
立体图形圆柱最短路径问题
知识点
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径。一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程。(结果保留根号)
2
立体图形圆柱最短路径问题
知识点
如图所示,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径。一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程。(结果保留根号)
A
B
C
D
解:如图所示,由题意可知:
BC=底面周长的一半=10cm,AB=4cm
在Rt△ABC中,由勾股定理得:
答:爬行的最短路程约为 cm。
o
变式:一只蚂蚁从点A出发,沿着圆柱的侧面爬行到CD的中点O,已知底面周长为10,试求出爬行的最短路程。
A
A
B
D
C
4
3
O
解:如图,由题意可知:
OD=4÷2=2,AD=10÷2=5。
在Rt△ABO中,由勾股定理得:
答:最短路程为 厘米。
3
立体图形正方体最短路径问题
知识点
如图,桌子上有一个边长为10cm且无盖的正方体型盒子,底面不可通行,若妈妈把食物放在正方体的C处,小黑蚂蚁从A点出发,沿着正方体的外表面爬行,则最短的路径的长是多少cm。
A
C
B
解:在Rt△ABC中,由勾股定理得:
AC=
经过前面和右面
3
立体图形正方体最短路径问题
知识点
如图,桌子上有一个边长为10cm且无盖的正方体型盒子,底面不可通行,若妈妈把食物放在正方体的C处,小黑蚂蚁从A点出发,沿着正方体的外表面爬行,则最短的路径的长是多少cm。
A
C
B
解:在Rt△ABC中,由勾股定理得:
AC=
经过左面和后面
提炼方法——
1、将立体图形展开,转化成平面图形。
2、在平面图中找到对应的起点和终点,即对应点位置。
3、在平面图形中,连接起点和终点,得出线段。
解:在Rt△ABC中,由勾股定理得:
4、构建直角三角形,利用勾股定理求出线段的长度,比较,得最短路径。
5、答题。
展
找
连
求
答
归纳总结:立体图形表面最短路径问题
方法:
立体图形
平面图形
直角三角形
建模
转化分类讨论
勾股定理
两点之间,线段最短
展
找
连
求
答
本节课数学思想
化归转化思想
4
立体图形长方体最短路径问题
知识点
如果盒子换成如图长为3cm,宽为2cm,高为1cm的长方体,蚂蚁沿着表面需要爬行的最短路程又是多少呢?
分析:蚂蚁由A爬到C1过程中较短的路线有多少种情况?
①经过前面和右面
②经过前面和上面
③经过左面和上面
①经过前面和右面
②经过前面和上面
③经过左面和上面
解:(1)当蚂蚁经过前面和右面时,最短路程为:
(2)当蚂蚁经过前面和上面时,最短路程为:
(3)当蚂蚁经过左面和上面时,最短路程为:
∴ 最短路程为 ㎝。
拓展提高:如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm、3cm、1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
A
B
C
D
解: 由题意可知:AC=5, BC=3×3+3×1=12
在Rt△ABC中,由勾股定理得:
答:从A点爬到B点,最短线路是13cm。
A
B
C
D
应用勾股定理解决实际问题的一般思路:
1、立体图形中路线最短的问题,往往是把立体图形展开,得到平面图形。根据“两点之间,线段最短” 确定行走路线,根据勾股定理计算出最短距离。
2、在解决实际问题时,首先要画出适当的示意图,将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题。
提炼方法——
立体图形
平面图形
直角三角形
建模
转化
勾股定理
两点之间,线段最短
化归转化思想
知识点
最短路径问题
本节课的数学思想
1.本节课学习了哪些知识?用了什么数学思想方法?
2.你们有什么收获?
总结反思
示例 长方体表面上A,B两点间的最短距离
作 业
练习册
谢谢欣赏
THANK YOU FOR LISTENING
如图,一个无盖长方形盒子的长、宽、高分别是4cm、4cm、6cm,一只蚂蚁想从盒底的A点沿盒的表面爬到盒顶的B点,蚂蚁要爬的最短路程是( )
A. 5cm B. 8cm C. 10cm D.7cm
解:长方体展开,将长方体展开,进而得出最短路线。
可得:AB2=62+82=100
∴AB=10(cm)
故最短路程为10cm。
C
B
A
A
B
6
4
4
练习1
不积跬步 无以至千里
意思是:行程千里,都是从一步一步开始;如果做事不从一点一滴中做起, 那就不可能有所成就。
【名人名言】
