高中数学人教A公开课课件:6.1.2分类加法计数原理与分步乘法计数原理 课件(共19张PPT)
文档属性
| 名称 | 高中数学人教A公开课课件:6.1.2分类加法计数原理与分步乘法计数原理 课件(共19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 13:37:04 | ||
图片预览






文档简介
(共19张PPT)
10.1计数原理
如果我和我们班的一位同学玩石头剪子布游戏,两个人各出一个手势,那么一共有多少种不同的出法?
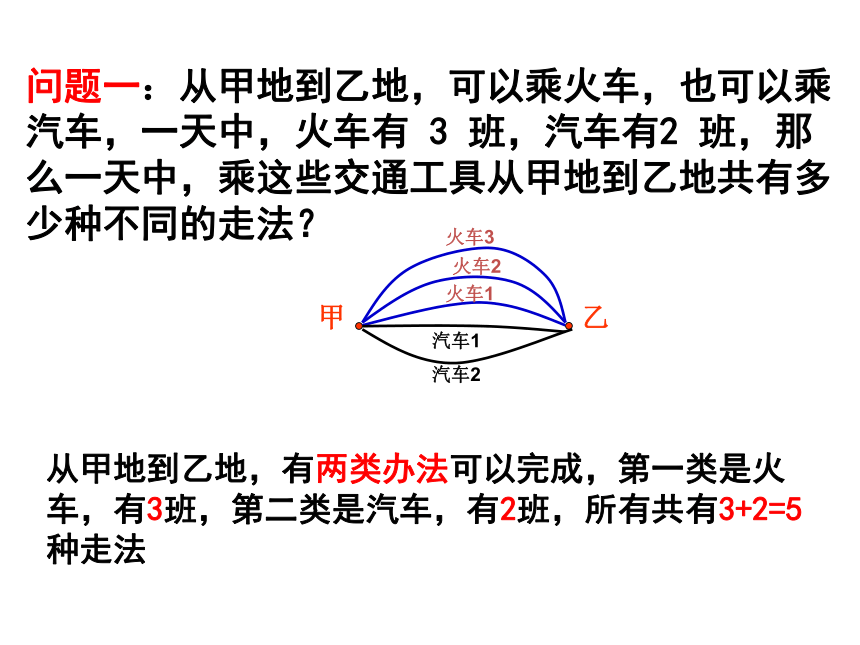
问题一:从甲地到乙地,可以乘火车,也可以乘汽车,一天中,火车有 3 班,汽车有2 班,那么一天中,乘这些交通工具从甲地到乙地共有多少种不同的走法?
从甲地到乙地,有两类办法可以完成,第一类是火车,有3班,第二类是汽车,有2班,所有共有3+2=5种走法
甲
乙
火车1
火车2
火车3
汽车1
汽车2
问题二 在填写高考志愿表时,一名高中生了解到A、B大学都有自己喜欢的强项专业,具体情况如下:
A大学:生物学,化学,医学,物理学,工程学
B大学:数学,会计学,信息技术学,法学
如果这名同学只能选择一个专业,那么他共有多少种选择呢?
共有:5+4=9 种
如果他又发现还有一个C大学也有自己的强项:新闻学,金融学,人力资源学,那么这时他一共有多少种选择呢?
共有:5+4+3=12 种
分类计数原理(加法原理):完成一件事,有n类办法,在第一类办法中有 m1 种不同的方法,在第二类办法中有 m2 种不同的方法,……,在第n类办法中有mn种不同的方法 那么完成这件事
共有 种不同的方法
问题三:从甲地到乙地,要从甲地先乘火车到丙地,再于次日从丙地乘汽车到乙地,一天中,火车有3班,汽车有2班,那么两天中,从甲地到乙地共有多少种不同的走法?
火车1──汽车1;火车1──汽车2
火车2──汽车1;火车2──汽车2
火车3──汽车1;火车3──汽车2
一共有:3×2=6 种
甲
乙
丙
火车3
火车2
火车1
汽车1
汽车2
问题四 我们班有男生20名,女生18名,现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
要选男女各一名代表班级参加比赛,要分两步完成,第一步从男生中选取一名,有20种方法;第二步从女生中选一名,有18种方法。
那么一共有 20×18=360 种
若问:从男、女生及2名课任教师各一名代表班级参加比赛,共有多少种不同的选法?
一共有 20×18×2=720 种
分步计数原理(乘法原理):完成一件事,需要分成n个步骤,做第一步有m1 种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事
共有 种不同的方法
分类计数原理(加法原理):完成一件事,有n类办法,在第一类办法中有 m1 种不同的方法,在第二类办法中有 m2 种不同的方法,……,在第n类办法中有mn种不同的方法 那么
完成这件事共有N=m1+m2+…+mn种不同的方法
你能比较分类计数原理与分步计数原理的异同点?
分步计数原理(乘法原理):完成一件事,需要分成n个步骤,做第一步有m1 种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事
共有N=m1╳m2 ╳ … ╳ mn 种不同的方法
①相同点:计算完成一件事的所有不同的方法种数
②不同点:
分类加法计数原理
(1)“分类”问题
(2) 各类方法不互相依存
(3)任何一类的任何一种方法都可以独立完成这件事
即:一步到位
分步乘法计数原理
(1)“分步”问题
(2)各个步骤相互依存
(2)完成任何其中的一步都不能完成该件事,只有当
各个步骤都完成后,才算完成这件事
即:多步到位
分类计数原理与分步计数原理的异同点
例1.书架的第1层放有4本不同的计算机书,第2层放有
3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同
的取法?
解:(1)完成“从书架上任取1本书”这件事,有3类办法:第1类是从第1层取1本计算机书,有4种方法;第2类是从第2层取1本文艺书,有3种方法;第3类是从第3层取1本体育书,有2种方法,根据分类计数原理,不同取法的种数是4+3+2=9种
(2)完成“从书架的第1、2、3层各取1本书”这件事,可以分成3个步骤完成:第1步从第1层取1本计算机书,有4种方法;第2步从第2层取1本艺术书,有3种方法;第3步从第3层取1本体育书,有2种方法,
根据分步计数原理,不同取法的种数是4╳3╳2=24种
例2.一种号码拨号锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数号码?
解:要确定一个四位数号码,需要分别从四个拨盘中各选一个号码。每个拨号盘上的数字有10种取法,根据分步计数原理,4个拨号盘上各取1个数字组成的四位数字号码的个数是10 ╳ 10 ╳ 10 ╳ 10=10000个
课堂练习
1 . 高中一年级学生3名,高中二年级学生5名,高中三
年级学生4名,
(1)从中任选1人参加接待外宾的活动,有多少种不同
的选法?
(2)从3个年级的学生中各选1人参加接待外宾的活动,
有多少种不同的选法?
解:(1)由分类计数原理得3+5+4=12 种
(2)由分步计数原理得3 ╳ 5 ╳ 4=60 种
2.如果我和我们班的一位同学玩石头剪子布游戏,两个人各出一个手势,那么一共有多少种不同的出法?
解:由分步计数原理得3╳3=9 种
3.从甲地到乙地有2种方法,从乙地到丙地有4种走法,从甲地不经过乙地到丙地有三种走法,则从甲地到丙地的不同走法共有多少种?
解:共有2╳4+3=11种
4.乘积
展开后共有多少项?
解:确定一个乘积结果aibjck,需要分三步完成,由分步计数原理可得
共有:3╳4╳5=60 项。
5.小明写了3封信,到了邮局后发现有并排的4只邮筒,那么他不同的投信方法有多少种?
能力挑战
6.甲、乙、丙三个班各有三好学生3、5、2名,现准备推选2名来自不同班的三好学生去参加校三好学生代表大会,共有多少种不同的推选方法?
我们的收获
1.分类计数(加法)原理
2.分步计数(乘法)原理
10.1计数原理
如果我和我们班的一位同学玩石头剪子布游戏,两个人各出一个手势,那么一共有多少种不同的出法?
问题一:从甲地到乙地,可以乘火车,也可以乘汽车,一天中,火车有 3 班,汽车有2 班,那么一天中,乘这些交通工具从甲地到乙地共有多少种不同的走法?
从甲地到乙地,有两类办法可以完成,第一类是火车,有3班,第二类是汽车,有2班,所有共有3+2=5种走法
甲
乙
火车1
火车2
火车3
汽车1
汽车2
问题二 在填写高考志愿表时,一名高中生了解到A、B大学都有自己喜欢的强项专业,具体情况如下:
A大学:生物学,化学,医学,物理学,工程学
B大学:数学,会计学,信息技术学,法学
如果这名同学只能选择一个专业,那么他共有多少种选择呢?
共有:5+4=9 种
如果他又发现还有一个C大学也有自己的强项:新闻学,金融学,人力资源学,那么这时他一共有多少种选择呢?
共有:5+4+3=12 种
分类计数原理(加法原理):完成一件事,有n类办法,在第一类办法中有 m1 种不同的方法,在第二类办法中有 m2 种不同的方法,……,在第n类办法中有mn种不同的方法 那么完成这件事
共有 种不同的方法
问题三:从甲地到乙地,要从甲地先乘火车到丙地,再于次日从丙地乘汽车到乙地,一天中,火车有3班,汽车有2班,那么两天中,从甲地到乙地共有多少种不同的走法?
火车1──汽车1;火车1──汽车2
火车2──汽车1;火车2──汽车2
火车3──汽车1;火车3──汽车2
一共有:3×2=6 种
甲
乙
丙
火车3
火车2
火车1
汽车1
汽车2
问题四 我们班有男生20名,女生18名,现要从中选出男、女生各一名代表班级参加比赛,共有多少种不同的选法?
要选男女各一名代表班级参加比赛,要分两步完成,第一步从男生中选取一名,有20种方法;第二步从女生中选一名,有18种方法。
那么一共有 20×18=360 种
若问:从男、女生及2名课任教师各一名代表班级参加比赛,共有多少种不同的选法?
一共有 20×18×2=720 种
分步计数原理(乘法原理):完成一件事,需要分成n个步骤,做第一步有m1 种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事
共有 种不同的方法
分类计数原理(加法原理):完成一件事,有n类办法,在第一类办法中有 m1 种不同的方法,在第二类办法中有 m2 种不同的方法,……,在第n类办法中有mn种不同的方法 那么
完成这件事共有N=m1+m2+…+mn种不同的方法
你能比较分类计数原理与分步计数原理的异同点?
分步计数原理(乘法原理):完成一件事,需要分成n个步骤,做第一步有m1 种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事
共有N=m1╳m2 ╳ … ╳ mn 种不同的方法
①相同点:计算完成一件事的所有不同的方法种数
②不同点:
分类加法计数原理
(1)“分类”问题
(2) 各类方法不互相依存
(3)任何一类的任何一种方法都可以独立完成这件事
即:一步到位
分步乘法计数原理
(1)“分步”问题
(2)各个步骤相互依存
(2)完成任何其中的一步都不能完成该件事,只有当
各个步骤都完成后,才算完成这件事
即:多步到位
分类计数原理与分步计数原理的异同点
例1.书架的第1层放有4本不同的计算机书,第2层放有
3本不同的文艺书,第3层放有2本不同的体育书,
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同
的取法?
解:(1)完成“从书架上任取1本书”这件事,有3类办法:第1类是从第1层取1本计算机书,有4种方法;第2类是从第2层取1本文艺书,有3种方法;第3类是从第3层取1本体育书,有2种方法,根据分类计数原理,不同取法的种数是4+3+2=9种
(2)完成“从书架的第1、2、3层各取1本书”这件事,可以分成3个步骤完成:第1步从第1层取1本计算机书,有4种方法;第2步从第2层取1本艺术书,有3种方法;第3步从第3层取1本体育书,有2种方法,
根据分步计数原理,不同取法的种数是4╳3╳2=24种
例2.一种号码拨号锁有4个拨号盘,每个拨号盘上有从0到9共10个数字,这4个拨号盘可以组成多少个四位数号码?
解:要确定一个四位数号码,需要分别从四个拨盘中各选一个号码。每个拨号盘上的数字有10种取法,根据分步计数原理,4个拨号盘上各取1个数字组成的四位数字号码的个数是10 ╳ 10 ╳ 10 ╳ 10=10000个
课堂练习
1 . 高中一年级学生3名,高中二年级学生5名,高中三
年级学生4名,
(1)从中任选1人参加接待外宾的活动,有多少种不同
的选法?
(2)从3个年级的学生中各选1人参加接待外宾的活动,
有多少种不同的选法?
解:(1)由分类计数原理得3+5+4=12 种
(2)由分步计数原理得3 ╳ 5 ╳ 4=60 种
2.如果我和我们班的一位同学玩石头剪子布游戏,两个人各出一个手势,那么一共有多少种不同的出法?
解:由分步计数原理得3╳3=9 种
3.从甲地到乙地有2种方法,从乙地到丙地有4种走法,从甲地不经过乙地到丙地有三种走法,则从甲地到丙地的不同走法共有多少种?
解:共有2╳4+3=11种
4.乘积
展开后共有多少项?
解:确定一个乘积结果aibjck,需要分三步完成,由分步计数原理可得
共有:3╳4╳5=60 项。
5.小明写了3封信,到了邮局后发现有并排的4只邮筒,那么他不同的投信方法有多少种?
能力挑战
6.甲、乙、丙三个班各有三好学生3、5、2名,现准备推选2名来自不同班的三好学生去参加校三好学生代表大会,共有多少种不同的推选方法?
我们的收获
1.分类计数(加法)原理
2.分步计数(乘法)原理
