云南省玉溪市一中2024-2025学年高二上学期第二次月考数学试题(含答案)
文档属性
| 名称 | 云南省玉溪市一中2024-2025学年高二上学期第二次月考数学试题(含答案) | 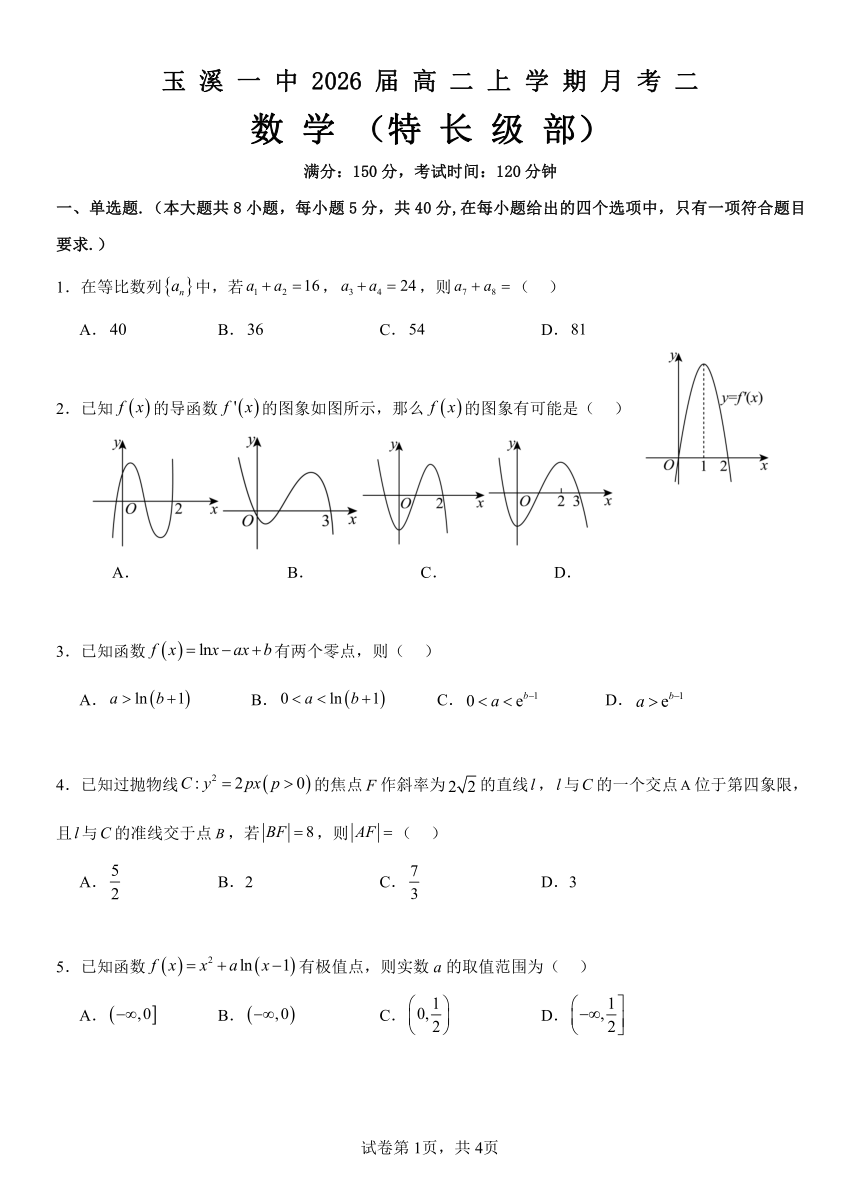 | |
| 格式 | |||
| 文件大小 | 394.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 15:33:00 | ||
图片预览




文档简介
玉 溪 一 中 2026 届 高 二 上 学 期 月 考 二
数 学 (特 长 级 部)
满分:150 分,考试时间:120 分钟
一、单选题.(本大题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中,只有一项符合题目
要求.)
1.在等比数列 an 中,若 a1 a2 16, a3 a4 24,则 a7 a8 ( )
A.40 B.36 C.54 D.81
2.已知 f x 的导函数 f ' x 的图象如图所示,那么 f x 的图象有可能是( )
A. B. C. D.
3.已知函数 f x lnx ax b有两个零点,则( )
A. a ln b 1 B.0 a ln b 1 C.0 a eb 1 D. a eb 1
4 2.已知过抛物线C : y 2px p 0 的焦点 F作斜率为 2 2的直线 l, l与C的一个交点A位于第四象限,
且 l与C的准线交于点 B,若 BF 8,则 AF ( )
5 7
A. B.2 C. D.3
2 3
5 f x x2.已知函数 a ln x 1 有极值点,则实数 a的取值范围为( )
A. , 0 , 0 B. C. 0,
1 1
D. ,
2 2
试卷第 1页,共 4页
{#{QQABLYQkExgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
6.在数列 an 中, an an 1 2n,则数列 an 前 24项和 S24的值为( )
A.144 B.312 C.288 D.156
7.已知圆C : (x 5)2 (y 3)2 3,直线 l : y ax 1,点M 、N为圆C上的两个动点,若直线 l上存在点 P,
使得 MPN 120 ,则 a的最大值为( )
7 6 21 20
A. B. C. D.
6 7 20 21
8.已知数列 an 满足 an 1 an 1 2an 2,a1 1,Sn是 an 的前 n项和.若 Sm 2024,则正整数m的所
有可能取值的个数为( )
A.48 B.50 C.52 D.54
二、多选题.(本大题共 3 小题,每小题 6 分,共 18 分, 在每小题给出的四个选项中,有多项符合题目要
求,全部选对得 6分,部分选对的得部分分,有选错的得 0 分.)
x2 y2 π π 9.已知双曲线 2 2 1(a 0,b 0)一条渐近线与实轴夹角为 ,且 , ,则离心率 e的可能取值a b 6 4
是( )
A 3 2. B 6. C. 2 D. 3
4 2
10.斐波那契数列又称“兔子数列”,在现代物理、化学等领域都有着广泛的应用.斐波那契数列 an 可以用
如下方法定义: F1 F2 1,Fn Fn 1 Fn 2 n 3,n N* .则( )
A. F12 145 B. F 2n FnFn 1 FnFn 1
C F 2 F 2 F 2. 1 2 n FnFn 1 D. F1 F2 Fn Fn 2 F2
11.已知 , ( )是函数 f (x) x3 ax2 bx 1 (a,b R)两个不同的零点,且 1, x1是函数 f (x)
的极大值点, x2是函数 f (x)的极小值点,则( )
A. 1是 f (x)的零点 B.1是 f (x)的零点 C. x1 D. x2
试卷第 2页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
三、填空题.(本大题共 3 小题,每小题 5 分,共 15 分.)
12.已知公差不为 0的等差数列 an 的前 n项和为 Sn,若 S9 3 a2 a4 am ,则m .
π π
13.在平行六面体 ABCD A1B1C1D1,中, AD BD, A1AD , A1AB= , AD BD AA3 4 1
1,则
A1C .
14.设 P x, y 是曲线 y cos x(0 x )上一动点,则 x+2y的最大值为 .
2
四、解答题.(本大题共 5 小题,共 77 分.写出必要的文字说明、证明过程或演算步骤)
15 13 2 2x.(本小题满分 分)已知函数 f x x e .
(1)求函数 f x 的单调区间;
(2)讨论方程 f x m(m R)解的个数.
3
16.(本小题满分 15分)已知数列 an 的前 n项和为 Sn, a1 且 S 2a2 n n 1
3 .
(1)求数列 an 的通项公式;
n2 n
(2)若bn ,求使bn取得最大值时的 n的值.an
试卷第 3页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
17.(本小题满分 15分)如图,在三棱柱 ABC A B C 中,平面 AA C C 平面 ABC,
AB AC BC AA1 2,A1B 6.
(1)设 D为 AC中点,证明: AC⊥平面 A1DB ;
(2)求平面 A1AB1与平面 ACC1A1夹角的余弦值.
18.(本小题满分 17分)已知函数 f (x) a ln(x 1), g(x) x 2 2x .
(1)如果函数 f (x)在 (2, f (2))处的切线,也是 g(x)的切线,求实数 a的值.
1
(2)若F(x) g(x) f (x)在 1,e 1
存在极小值 F x
e 0
,试求 F x0 的范围.
19.(本小题满分 17分)已知在平面直角坐标系 xOy中,椭圆G的中心在坐标原点O,焦点在 x轴上,焦
3
距等于 2 6 ,离心率为
2
(1)求椭圆G的标准方程;
1
(2)若直线 y x m(m 0)与椭圆G交于 M、N两点,求证: |OM |2 |ON |2 为定值;
2
(3)记 B为椭圆上顶点,过点 B作相互垂直的两条直线 BP,BQ分别与椭圆G相交于 P,Q两点.设直线 BP
的斜率为 k且 k 0,若 | BP | | BQ |,求 k的值.
试卷第 4页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
玉 溪 一 中 2026 届 高 二 上 学 期 月 考 二
数学(特长级部)参考答案
一、单选题
题号 1 2 3 4 5 6 7 8
答案 C D C B B C D D
二、多选题
题号 9 10 11
答案 BC BCD AD
三、填空题
12.9 13. 2 14. 36
四、解答题
15.(1) f x 2x 2的定义域为R , f x 2xe x 2e2x x x2 2e2x,
由�� � � �,可得 1 x 0,由 f x 0,可得 x 1或 � �,
∴函数 f x 的单调递减区间是 1,0 ,单调递增区间是 , 1 , 0, . ……6分
(2)由(1)可知函数 f x 在 , 1 , � ∞ 上单调递增;函数 f x 在 1,0 上单调递减,
∴ f x 1在 x 1时函数取极大值: f 1 2 ; f x 在 x 0时函数取极小值: f 0 0,e
又∵ x2 0, e x 0 2 2x ,∴ f x x e 0,
可得函数的大致图象,
∴当m 0时, f x m有 0个解;
1
当m 0或m 时, f x m有 1个解;
e2
0 m 1当 2 时, f x me 有 3个解;
1
当m 2 时, f x m有 2个解. ……13分e
答案第 1页,共 4页
{#{QQABLYQkExgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
16. (1)由 Sn 2an 1 3,可得: Sn 1 2an 3(n 2)两式相减得: an Sn Sn 1 2an 1 2an
a
n 2 n 1
3
即 , a , ……4分n 2
a 3 a 3
又因为 S 31 2a2 3且 S1 a1 ,所以 a
9 2 n 1
2 ,所以 a 2,综上, n 1,
2 4 1 a 2
,
n
a 3 . a a qn 1 3
n
所以 n 为首项和公比均为 的等比数列 n 1 ……7分2 2
2 n2 ( )由(1)可得,所以bn 3 n
2 n ,
2 n2b n 2 n 1
n 2时,由 n 1,可得 n 5;故当 n 5,b4 b ,bn 1 3 n2 n 3 n 1 5
当n 5时,b5 b6 b7 因此b2 b3 b4 b5 b6 b7
4 4 8
又 Q b1 ,b2 6 , b1 b2,即b1 b b b b b b ,3 9 3 2 3 4 5 6 7
320
综上, n 4或 n 5时,bn的取得最大值 . ……15分81
17.(1)证明:因为D为 AC中点,且 AB AC BC 2,所以在V ABC中,有 BD AC,且 BD 3,
又平面 ACC1A1 平面 ABC,且平面 ACC1A1 平面 ABC AC, BD 平面 ABC ,
所以 BD 平面 ACC1A1,又 A1D 平面 ACC1A1,则 BD A1D,
由 A1B 6,BD 3,得 A1D 3,
因为 AD 1, AA1 2, A1D 3,所以由勾股定理,得 AC A1D,
又 AC BD, A1D BD D, A1D,BD 平面 A1DB,所以 AC 平面 A1DB; ……7分
(2)如图所示,以(1)中的D为原点,建立空间直角坐标系D xyz,
可得 A(1,0,0),A1(0,0, 3),B(0, 3,0),
则 AA1 1,0, 3 , AB 1, 3,0 ,
设平面 A1AB1的法向量为 n (x, y, z),
n AA
1
x 3z 0
由 ,令 x 3,得 y 1,z 1,所以 n 3,1,1 ,
n AB x 3y 0
答案第 2页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
由(1)知,BD 平面 ACC1A1,所以平面 ACC1A1的一个法向量为 BD (0, 3,0),
记平面 A1AB1与平面 ACC A
| n BD | 3 5
1 1的夹角为 ,则 cos ,| n || BD | 5 3 5
5
所以平面 A1AB1与平面 ACC1A1夹角的余弦值为 . …… 15分
5
a
18.(1) f (2) 0, f (x) , f (2) a,故 f (x)在 (2, f (2))处的切线为 y a x 2 ,
x 1
y a x 2 也是 g(x)的切线,
故方程 a x 2 x2 2x 2只有一个解,即 x a 2 x 2a 0只有一个解,
a 2 2 8a 0,解得a 2 . …… 7分
2 x 1 2(2) F (x) g(x) f (x) x2 2x a ln x 1 , F (x) 2x 2 a a ,
x 1 x 1
当 a 0时, F (x) 0,F (x)无极值点,不符合题意;
a
当 a 0时,在 1,1 上, F (x) 0, F (x)单调递减;
2
a
在 1 , 上, F (x) 0, F (x)单调递增;
2
故 F (x) a 2的极小值点 x0 1 ,则 a 2 x0 1 , …… 12分2
故 F x0 x 20 2x0 2 x0 1
2 ln x0 1 ,
设 t x0 1, x
1
0 1,e 1
1 2 2
,则 t ,e e e
,此时F x0 t 1 2t ln t,
设 h t t 2 1 2t 2 ln t,则 h t 4t ln t,
t 1 ,1 时, h t 0, h t 单调递增; t 1,e 时, h t 0, h t 单调递减;
e
h 1 3
2 2 2
e e2
1,h e e 1,h 1 0 ,故 h t e 1,0 ,即 F x0 e 1,0 ……17分
19.(1 3 c)由已知得 c 6,又 e , a 2 2,又b2 a2 c2 2 .
2 a
G x
2 y2
所以椭圆 的方程为 1 . ……4分
8 2
答案第 3页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
1
(2)依题意,设M x1, y1 ,N
y x mx2 , y2 ,联立直线与椭圆G有 2 ,消元得:x2 2mx 2m2 4 0
2 2 x 4y 8
当 16 4m2 0,即m2 4且m 0 2时, x1 x2 2m, x1x2 2m 4,
x2 x2|OM |2 |ON |2 x2 1 2 2
3 2 2
1 2 1 x2 2 1 4 x1 x2 4 3 x x 2 2x 8 8 4 4 1 2 1x2
3
4 4m2 4m2 8 10,即 |OM |2 |ON |2 10为定值. ……10分4
(3)设 P xP , yP ,N xQ , yQ ,设直线 BP的方程为 y kx 2(k 0),
x2 y2
1 1
则直线 BQ的方程为 y x 2 ,由 8 2 ,消去 y 1 4k 2得 x2 8 2kx 0,k
y kx 2
x 8 2k | BP | 1 k2 x x 8 2k 1 k
2
P , ,1 4k 2 B P 1 4k 2
x2 y2
1
8 2 4 8 2x 2
由 得 1
x22 0, x
8 2k
x Q | BQ | 1
1 x x 8 2 1 k, ,
k k k 2 4 k 2 B
Q 2
y 2 4 k
k
2 2
Q | BP | | BQ | 8 2 1 k 8 2k 1 k, ,
4 k 2 1 4k 2
整理得: k 3 4k 2 4k 1 0 2, (k 1) k 3k 1 0, k 1 k 3 5或 . …… 17分
2
答案第 4页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
数 学 (特 长 级 部)
满分:150 分,考试时间:120 分钟
一、单选题.(本大题共 8 小题,每小题 5 分,共 40 分,在每小题给出的四个选项中,只有一项符合题目
要求.)
1.在等比数列 an 中,若 a1 a2 16, a3 a4 24,则 a7 a8 ( )
A.40 B.36 C.54 D.81
2.已知 f x 的导函数 f ' x 的图象如图所示,那么 f x 的图象有可能是( )
A. B. C. D.
3.已知函数 f x lnx ax b有两个零点,则( )
A. a ln b 1 B.0 a ln b 1 C.0 a eb 1 D. a eb 1
4 2.已知过抛物线C : y 2px p 0 的焦点 F作斜率为 2 2的直线 l, l与C的一个交点A位于第四象限,
且 l与C的准线交于点 B,若 BF 8,则 AF ( )
5 7
A. B.2 C. D.3
2 3
5 f x x2.已知函数 a ln x 1 有极值点,则实数 a的取值范围为( )
A. , 0 , 0 B. C. 0,
1 1
D. ,
2 2
试卷第 1页,共 4页
{#{QQABLYQkExgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
6.在数列 an 中, an an 1 2n,则数列 an 前 24项和 S24的值为( )
A.144 B.312 C.288 D.156
7.已知圆C : (x 5)2 (y 3)2 3,直线 l : y ax 1,点M 、N为圆C上的两个动点,若直线 l上存在点 P,
使得 MPN 120 ,则 a的最大值为( )
7 6 21 20
A. B. C. D.
6 7 20 21
8.已知数列 an 满足 an 1 an 1 2an 2,a1 1,Sn是 an 的前 n项和.若 Sm 2024,则正整数m的所
有可能取值的个数为( )
A.48 B.50 C.52 D.54
二、多选题.(本大题共 3 小题,每小题 6 分,共 18 分, 在每小题给出的四个选项中,有多项符合题目要
求,全部选对得 6分,部分选对的得部分分,有选错的得 0 分.)
x2 y2 π π 9.已知双曲线 2 2 1(a 0,b 0)一条渐近线与实轴夹角为 ,且 , ,则离心率 e的可能取值a b 6 4
是( )
A 3 2. B 6. C. 2 D. 3
4 2
10.斐波那契数列又称“兔子数列”,在现代物理、化学等领域都有着广泛的应用.斐波那契数列 an 可以用
如下方法定义: F1 F2 1,Fn Fn 1 Fn 2 n 3,n N* .则( )
A. F12 145 B. F 2n FnFn 1 FnFn 1
C F 2 F 2 F 2. 1 2 n FnFn 1 D. F1 F2 Fn Fn 2 F2
11.已知 , ( )是函数 f (x) x3 ax2 bx 1 (a,b R)两个不同的零点,且 1, x1是函数 f (x)
的极大值点, x2是函数 f (x)的极小值点,则( )
A. 1是 f (x)的零点 B.1是 f (x)的零点 C. x1 D. x2
试卷第 2页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
三、填空题.(本大题共 3 小题,每小题 5 分,共 15 分.)
12.已知公差不为 0的等差数列 an 的前 n项和为 Sn,若 S9 3 a2 a4 am ,则m .
π π
13.在平行六面体 ABCD A1B1C1D1,中, AD BD, A1AD , A1AB= , AD BD AA3 4 1
1,则
A1C .
14.设 P x, y 是曲线 y cos x(0 x )上一动点,则 x+2y的最大值为 .
2
四、解答题.(本大题共 5 小题,共 77 分.写出必要的文字说明、证明过程或演算步骤)
15 13 2 2x.(本小题满分 分)已知函数 f x x e .
(1)求函数 f x 的单调区间;
(2)讨论方程 f x m(m R)解的个数.
3
16.(本小题满分 15分)已知数列 an 的前 n项和为 Sn, a1 且 S 2a2 n n 1
3 .
(1)求数列 an 的通项公式;
n2 n
(2)若bn ,求使bn取得最大值时的 n的值.an
试卷第 3页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
17.(本小题满分 15分)如图,在三棱柱 ABC A B C 中,平面 AA C C 平面 ABC,
AB AC BC AA1 2,A1B 6.
(1)设 D为 AC中点,证明: AC⊥平面 A1DB ;
(2)求平面 A1AB1与平面 ACC1A1夹角的余弦值.
18.(本小题满分 17分)已知函数 f (x) a ln(x 1), g(x) x 2 2x .
(1)如果函数 f (x)在 (2, f (2))处的切线,也是 g(x)的切线,求实数 a的值.
1
(2)若F(x) g(x) f (x)在 1,e 1
存在极小值 F x
e 0
,试求 F x0 的范围.
19.(本小题满分 17分)已知在平面直角坐标系 xOy中,椭圆G的中心在坐标原点O,焦点在 x轴上,焦
3
距等于 2 6 ,离心率为
2
(1)求椭圆G的标准方程;
1
(2)若直线 y x m(m 0)与椭圆G交于 M、N两点,求证: |OM |2 |ON |2 为定值;
2
(3)记 B为椭圆上顶点,过点 B作相互垂直的两条直线 BP,BQ分别与椭圆G相交于 P,Q两点.设直线 BP
的斜率为 k且 k 0,若 | BP | | BQ |,求 k的值.
试卷第 4页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
玉 溪 一 中 2026 届 高 二 上 学 期 月 考 二
数学(特长级部)参考答案
一、单选题
题号 1 2 3 4 5 6 7 8
答案 C D C B B C D D
二、多选题
题号 9 10 11
答案 BC BCD AD
三、填空题
12.9 13. 2 14. 36
四、解答题
15.(1) f x 2x 2的定义域为R , f x 2xe x 2e2x x x2 2e2x,
由�� � � �,可得 1 x 0,由 f x 0,可得 x 1或 � �,
∴函数 f x 的单调递减区间是 1,0 ,单调递增区间是 , 1 , 0, . ……6分
(2)由(1)可知函数 f x 在 , 1 , � ∞ 上单调递增;函数 f x 在 1,0 上单调递减,
∴ f x 1在 x 1时函数取极大值: f 1 2 ; f x 在 x 0时函数取极小值: f 0 0,e
又∵ x2 0, e x 0 2 2x ,∴ f x x e 0,
可得函数的大致图象,
∴当m 0时, f x m有 0个解;
1
当m 0或m 时, f x m有 1个解;
e2
0 m 1当 2 时, f x me 有 3个解;
1
当m 2 时, f x m有 2个解. ……13分e
答案第 1页,共 4页
{#{QQABLYQkExgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
16. (1)由 Sn 2an 1 3,可得: Sn 1 2an 3(n 2)两式相减得: an Sn Sn 1 2an 1 2an
a
n 2 n 1
3
即 , a , ……4分n 2
a 3 a 3
又因为 S 31 2a2 3且 S1 a1 ,所以 a
9 2 n 1
2 ,所以 a 2,综上, n 1,
2 4 1 a 2
,
n
a 3 . a a qn 1 3
n
所以 n 为首项和公比均为 的等比数列 n 1 ……7分2 2
2 n2 ( )由(1)可得,所以bn 3 n
2 n ,
2 n2b n 2 n 1
n 2时,由 n 1,可得 n 5;故当 n 5,b4 b ,bn 1 3 n2 n 3 n 1 5
当n 5时,b5 b6 b7 因此b2 b3 b4 b5 b6 b7
4 4 8
又 Q b1 ,b2 6 , b1 b2,即b1 b b b b b b ,3 9 3 2 3 4 5 6 7
320
综上, n 4或 n 5时,bn的取得最大值 . ……15分81
17.(1)证明:因为D为 AC中点,且 AB AC BC 2,所以在V ABC中,有 BD AC,且 BD 3,
又平面 ACC1A1 平面 ABC,且平面 ACC1A1 平面 ABC AC, BD 平面 ABC ,
所以 BD 平面 ACC1A1,又 A1D 平面 ACC1A1,则 BD A1D,
由 A1B 6,BD 3,得 A1D 3,
因为 AD 1, AA1 2, A1D 3,所以由勾股定理,得 AC A1D,
又 AC BD, A1D BD D, A1D,BD 平面 A1DB,所以 AC 平面 A1DB; ……7分
(2)如图所示,以(1)中的D为原点,建立空间直角坐标系D xyz,
可得 A(1,0,0),A1(0,0, 3),B(0, 3,0),
则 AA1 1,0, 3 , AB 1, 3,0 ,
设平面 A1AB1的法向量为 n (x, y, z),
n AA
1
x 3z 0
由 ,令 x 3,得 y 1,z 1,所以 n 3,1,1 ,
n AB x 3y 0
答案第 2页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
由(1)知,BD 平面 ACC1A1,所以平面 ACC1A1的一个法向量为 BD (0, 3,0),
记平面 A1AB1与平面 ACC A
| n BD | 3 5
1 1的夹角为 ,则 cos ,| n || BD | 5 3 5
5
所以平面 A1AB1与平面 ACC1A1夹角的余弦值为 . …… 15分
5
a
18.(1) f (2) 0, f (x) , f (2) a,故 f (x)在 (2, f (2))处的切线为 y a x 2 ,
x 1
y a x 2 也是 g(x)的切线,
故方程 a x 2 x2 2x 2只有一个解,即 x a 2 x 2a 0只有一个解,
a 2 2 8a 0,解得a 2 . …… 7分
2 x 1 2(2) F (x) g(x) f (x) x2 2x a ln x 1 , F (x) 2x 2 a a ,
x 1 x 1
当 a 0时, F (x) 0,F (x)无极值点,不符合题意;
a
当 a 0时,在 1,1 上, F (x) 0, F (x)单调递减;
2
a
在 1 , 上, F (x) 0, F (x)单调递增;
2
故 F (x) a 2的极小值点 x0 1 ,则 a 2 x0 1 , …… 12分2
故 F x0 x 20 2x0 2 x0 1
2 ln x0 1 ,
设 t x0 1, x
1
0 1,e 1
1 2 2
,则 t ,e e e
,此时F x0 t 1 2t ln t,
设 h t t 2 1 2t 2 ln t,则 h t 4t ln t,
t 1 ,1 时, h t 0, h t 单调递增; t 1,e 时, h t 0, h t 单调递减;
e
h 1 3
2 2 2
e e2
1,h e e 1,h 1 0 ,故 h t e 1,0 ,即 F x0 e 1,0 ……17分
19.(1 3 c)由已知得 c 6,又 e , a 2 2,又b2 a2 c2 2 .
2 a
G x
2 y2
所以椭圆 的方程为 1 . ……4分
8 2
答案第 3页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
1
(2)依题意,设M x1, y1 ,N
y x mx2 , y2 ,联立直线与椭圆G有 2 ,消元得:x2 2mx 2m2 4 0
2 2 x 4y 8
当 16 4m2 0,即m2 4且m 0 2时, x1 x2 2m, x1x2 2m 4,
x2 x2|OM |2 |ON |2 x2 1 2 2
3 2 2
1 2 1 x2 2 1 4 x1 x2 4 3 x x 2 2x 8 8 4 4 1 2 1x2
3
4 4m2 4m2 8 10,即 |OM |2 |ON |2 10为定值. ……10分4
(3)设 P xP , yP ,N xQ , yQ ,设直线 BP的方程为 y kx 2(k 0),
x2 y2
1 1
则直线 BQ的方程为 y x 2 ,由 8 2 ,消去 y 1 4k 2得 x2 8 2kx 0,k
y kx 2
x 8 2k | BP | 1 k2 x x 8 2k 1 k
2
P , ,1 4k 2 B P 1 4k 2
x2 y2
1
8 2 4 8 2x 2
由 得 1
x22 0, x
8 2k
x Q | BQ | 1
1 x x 8 2 1 k, ,
k k k 2 4 k 2 B
Q 2
y 2 4 k
k
2 2
Q | BP | | BQ | 8 2 1 k 8 2k 1 k, ,
4 k 2 1 4k 2
整理得: k 3 4k 2 4k 1 0 2, (k 1) k 3k 1 0, k 1 k 3 5或 . …… 17分
2
答案第 4页,共 4页
{#{QQABLYQEkxgggiQiAgAAAaIAACQI5gqCAAwwmngwCCEEgMQQsokGhCiLCegCMSRgOVRANFAKAIRACAyAQCNRANBAIBAA=}A#=} }#}
同课章节目录
