青岛版八年级下册10.3 一次函数的性质 课件(共23张PPT)
文档属性
| 名称 | 青岛版八年级下册10.3 一次函数的性质 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 08:16:35 | ||
图片预览






文档简介
(共23张PPT)
10.3一次函数的性质
初中数学 八年级下册 青岛出版社
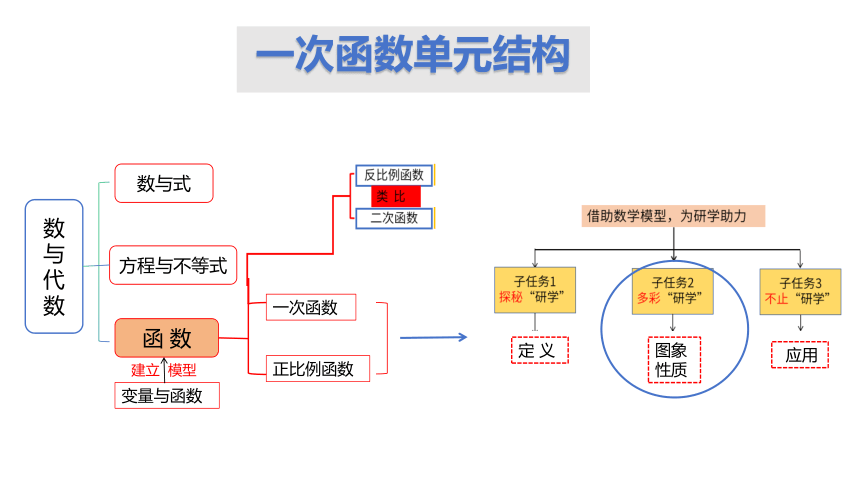
一次函数单元结构
数与式
方程与不等式
函 数
数
与
代数
变量与函数
建立 模型
一次函数
正比例函数
定 义
图象性质
应用
学习目标
通过预习导入和新知探究,借助图象观察、猜想、验证,归纳,探索一次函数的性质和k、b的符号与与一次函数的图象之间的关系,体会从特殊到一般的数学思想。
通过典例导引、即时检测等应用一次函数的性质解决问题,体会数形结合和分类讨论思想,提高分析问题、解决问题的能力。
1
2
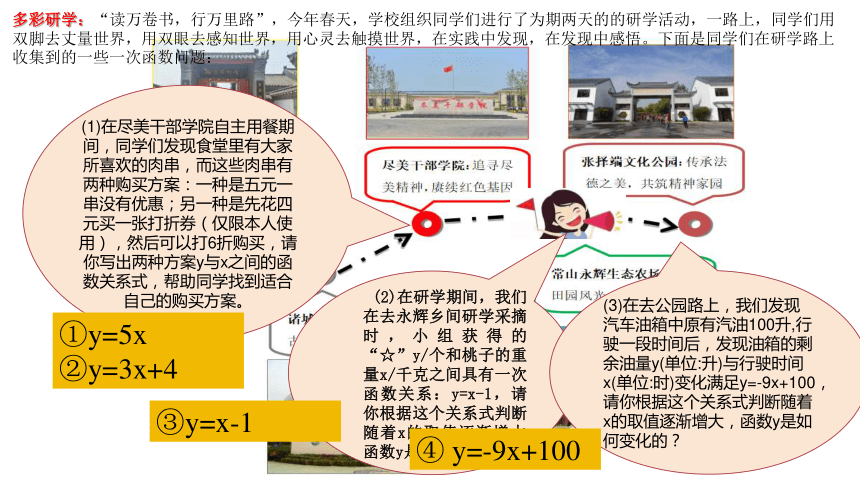
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(2)在研学期间,我们在去永辉乡间研学采摘时,小组获得的“☆”y/个和桃子的重量x/千克之间具有一次函数关系:y=x-1,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
③y=x-1
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(2)在研学期间,我们在去永辉乡间研学采摘时,小组获得的“☆”y/个和桃子的重量x/千克之间具有一次函数关系:y=x-1,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
③y=x-1
(3)在去公园路上,我们发现汽车油箱中原有汽油100升,行驶一段时间后,发现油箱的剩余油量y(单位:升)与行驶时间x(单位:时)变化满足y=-9x+100,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
④ y=-9x+100
①y=5x
②y=3x+4
③y=x-1
④ y=-9x+100
在一次函数y=kx+b中,你认为K和b的符号
可以分为几类?体现了什么数学思想?
K>0
K<0
一
二
四
三
x
y=3x+4
-4
0
4
5
3
2
1
2
3
-1
-2
-1
-2
-3
1
y
y=x-1
y=5x
1.图象从左向右是什么变化趋势(升高还是降低)?
2.设P(x,y)是直线的一个动点,随着P点从左往右移动,横坐标x和纵坐标y发生怎样的变化?
3.当k>0时,其他一次函数是否也具有上述性质?
任务一:探索一次函数的性质和k、b的符号与一次函数的图象之间的关系
分类讨论
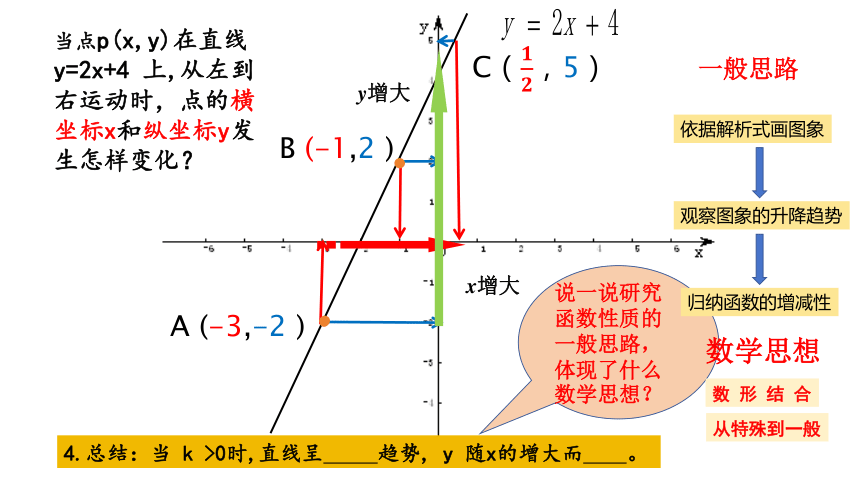
A (-3,-2 )
B (-1,2 )
x增大
y增大
当点p(x,y)在直线y=2x+4 上,从左到右运动时,点的横坐标x和纵坐标y发生怎样变化?
C(,5)
4.总结:当 k >0时,直线呈 趋势, y 随x的增大而 。
依据解析式画图象
说一说研究函数性质的一般思路,体现了什么数学思想?
观察图象的升降趋势
归纳函数的增减性
数 形 结 合
从特殊到一般
一般思路
数学思想
5.观察解析式,类比 k >0时一次函数性质的探究思路,总结当 k <0时,直线呈 趋势, y 随x的增大而 。
6.能力提升:直线倾斜程度与K之间的关系。
x
一
三
四
二
结论:
|k|越大,直线越陡,越靠近y轴,相应的函数值上升或下降得越快。
数形结合
任务一:探索一次函数的性质和k、b的符号与一次函数的图象之间的关系
0
4
5
3
2
1
2
3
-1
-2
4
-1
-2
-3
1
y
y=-3x-1
y=-x+2
分类讨论
类比:
1.图象从左向右是什么变化趋势(升高还是降低)?
2.设P(x,y)是直线的一个动点,随着P点从左往右移动,横坐标x和纵坐标y发生怎样的变化?
3.当k>0时,其他一次函数是否也具有上述性质?
活动2:探究k、b的符号与一次函数的图象之间的关系
1.通过活动一我们知道当k >0时直线呈 趋势, k < O 时直线呈 趋势;上节中我们学习了b >0 时图象与y轴交于 半轴,b=0时图象与y轴交于 ,b < O时图象与y轴交于 半轴。
2.对于一次函数y=kx+b的图象,其中的k值与b值分别决定的是什么?
任务一:探索一次函数的性质和k、b的符号与一次函数的图象之间的关系
3.请利用上述结论画出对应一次函数的草图并判断经过的象限
x
y
0
x
y
0
y
x
0
x
y
0
x
y
0
x
y
0
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
增大
减小
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(2)在研学期间,我们在去永辉乡间研学采摘时,小组获得的“☆”y/个和桃子的重量x/千克之间具有一次函数关系:y=x-1,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
③y=x-1
(3)在去公园路上,我们发现汽车油箱中原有汽油100升,行驶一段时间后,发现油箱的剩余油量y(单位:升)与行驶时间x(单位:时)变化满足y=-9x+100,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
④ y=-9x+100
①y=5x
②y=3x+4
x
已知一次函数 y=(m+2) x + 3 ,当 m为何值时,y随x的增大而减小?
解:根据一次函数的性质,
当m+2<0时,y随x的增大而减小.
解不等式m+2<0,得m<-2.
所以,当m<-2时,y随x的增大而减小.
评价一:(对应目标1)
评价一
得分:
每题10分,共20分
已知一次函数y=kx-k,且y随x的增大而增大,试探索的图象经过哪几个象限?
解:
因为一次函数y=kx-k的y随x的增大而增大,所以k>0;
b=-k<0,这条直线经过第一、三、四象限.
评价二:(对应目标1)
评价一
得分:
每题10分,共20分
活动1:合作完成例题,方法尽量多
例1: (1)如果点(-2,m)和(0.5,n)都在直线y=3x+4上,至少用两种方法比较m和n的大小。
(2)(优生优培,选做)如果点(-2,m)和(0.5,n)都在直线y=kx+b(k<0)上,比较m和n的大小。
任务二:应用一次函数的性质解决问题
法一:直接代入,求出m、n的值进比较
法二:应用一次函数的增减性
法三:数形结合
1.点A(3,y1)和点B(-2,y2)都在直线y=-2x+3上,则y1和y2的大小关系是 ( )
A.y1>y2 B.y1评价:(对应目标2)
评价一
得分:
每题5分,共10分
B
2.(多选)下列结论中正确的有( )
A 点M(x1,y1)和N(x2,y2)都在直线y=2x-1上,若x1>x2,则y1>y2
B 直线y=-3x-4经过一、二、四象限
C 直线y=3x-1不经过第二象限
D 直线y=-x-4和直线y=x-4交点在y轴上
ACD
数形结合
分类讨论
依据解析式画图象
观察图象的升降趋势
归纳函数的增减性
从特殊
到一般
一般思路
数学思想
当堂检测得分:
每题10分,共40分
A组
1.下列函数中,y的值随x值的增大而增大的函数是( )
A.y= -2x B.y= -2x+1 C.y=x-2 D.y= -x-2
2.当1<k<2时,一次函数y=kx﹣2x+k的图象一定不过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知(x1,y1)和(x2,y2)是直线y=-3x上的两点,且x1>x2,则y1与y2大小关系是( )
A.y1>y2 B.y14.已知函数y= 是一次函数且y随x的增大而增大,求m的取值 .
C
C
B
m=4
当堂检测得分:
每题10分,共30分
B组
5.若一次函数y=kx+3的图象经与y=-4x平行,那么这个函数的表达式为_________,y的值随x 的增大而_________。
6.如果直线y=kx+b经过一、三、四象限,那么直线y=-bx+k经过哪几个象限?
7.王老师让同学考虑一个一次函数,请小亮、小莹、大刚、王强分别对这个函数提出一个性质:
小亮:函数图象经过第二象限,不经过第三象限;
小莹:当x>0时,y<0;
大刚:y随着x的增大而减小;
王强:当x=-2时,y=3.
请画出同时适合上面四个条件的一个一次函数的图象
y=-4x+3
减小
一、二、三
当堂检测得分:
10+20分,共30分
8.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是( )
A.0 B.2 C.3 D.4
9.己知关于x的一次函数y=mx+4m 2,
(1)若这个函数的图象经过原点,求m的值;
(2)若这个函数的图象不过第四象限,求m的取值范围;
(3)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标。
C组
B
m=
m≥
(-4,-2)
课后作业
类比一次函数性质的研究思路,研究函数y=x2+1的性质。
10.3一次函数的性质
初中数学 八年级下册 青岛出版社
一次函数单元结构
数与式
方程与不等式
函 数
数
与
代数
变量与函数
建立 模型
一次函数
正比例函数
定 义
图象性质
应用
学习目标
通过预习导入和新知探究,借助图象观察、猜想、验证,归纳,探索一次函数的性质和k、b的符号与与一次函数的图象之间的关系,体会从特殊到一般的数学思想。
通过典例导引、即时检测等应用一次函数的性质解决问题,体会数形结合和分类讨论思想,提高分析问题、解决问题的能力。
1
2
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(2)在研学期间,我们在去永辉乡间研学采摘时,小组获得的“☆”y/个和桃子的重量x/千克之间具有一次函数关系:y=x-1,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
③y=x-1
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(2)在研学期间,我们在去永辉乡间研学采摘时,小组获得的“☆”y/个和桃子的重量x/千克之间具有一次函数关系:y=x-1,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
③y=x-1
(3)在去公园路上,我们发现汽车油箱中原有汽油100升,行驶一段时间后,发现油箱的剩余油量y(单位:升)与行驶时间x(单位:时)变化满足y=-9x+100,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
④ y=-9x+100
①y=5x
②y=3x+4
③y=x-1
④ y=-9x+100
在一次函数y=kx+b中,你认为K和b的符号
可以分为几类?体现了什么数学思想?
K>0
K<0
一
二
四
三
x
y=3x+4
-4
0
4
5
3
2
1
2
3
-1
-2
-1
-2
-3
1
y
y=x-1
y=5x
1.图象从左向右是什么变化趋势(升高还是降低)?
2.设P(x,y)是直线的一个动点,随着P点从左往右移动,横坐标x和纵坐标y发生怎样的变化?
3.当k>0时,其他一次函数是否也具有上述性质?
任务一:探索一次函数的性质和k、b的符号与一次函数的图象之间的关系
分类讨论
A (-3,-2 )
B (-1,2 )
x增大
y增大
当点p(x,y)在直线y=2x+4 上,从左到右运动时,点的横坐标x和纵坐标y发生怎样变化?
C(,5)
4.总结:当 k >0时,直线呈 趋势, y 随x的增大而 。
依据解析式画图象
说一说研究函数性质的一般思路,体现了什么数学思想?
观察图象的升降趋势
归纳函数的增减性
数 形 结 合
从特殊到一般
一般思路
数学思想
5.观察解析式,类比 k >0时一次函数性质的探究思路,总结当 k <0时,直线呈 趋势, y 随x的增大而 。
6.能力提升:直线倾斜程度与K之间的关系。
x
一
三
四
二
结论:
|k|越大,直线越陡,越靠近y轴,相应的函数值上升或下降得越快。
数形结合
任务一:探索一次函数的性质和k、b的符号与一次函数的图象之间的关系
0
4
5
3
2
1
2
3
-1
-2
4
-1
-2
-3
1
y
y=-3x-1
y=-x+2
分类讨论
类比:
1.图象从左向右是什么变化趋势(升高还是降低)?
2.设P(x,y)是直线的一个动点,随着P点从左往右移动,横坐标x和纵坐标y发生怎样的变化?
3.当k>0时,其他一次函数是否也具有上述性质?
活动2:探究k、b的符号与一次函数的图象之间的关系
1.通过活动一我们知道当k >0时直线呈 趋势, k < O 时直线呈 趋势;上节中我们学习了b >0 时图象与y轴交于 半轴,b=0时图象与y轴交于 ,b < O时图象与y轴交于 半轴。
2.对于一次函数y=kx+b的图象,其中的k值与b值分别决定的是什么?
任务一:探索一次函数的性质和k、b的符号与一次函数的图象之间的关系
3.请利用上述结论画出对应一次函数的草图并判断经过的象限
x
y
0
x
y
0
y
x
0
x
y
0
x
y
0
x
y
0
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
增大
减小
多彩研学:“读万卷书,行万里路”,今年春天,学校组织同学们进行了为期两天的的研学活动,一路上,同学们用双脚去丈量世界,用双眼去感知世界,用心灵去触摸世界,在实践中发现,在发现中感悟。下面是同学们在研学路上收集到的一些一次函数问题:
(2)在研学期间,我们在去永辉乡间研学采摘时,小组获得的“☆”y/个和桃子的重量x/千克之间具有一次函数关系:y=x-1,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
(1)在尽美干部学院自主用餐期间,同学们发现食堂里有大家所喜欢的肉串,而这些肉串有两种购买方案:一种是五元一串没有优惠;另一种是先花四元买一张打折券(仅限本人使用),然后可以打6折购买,请你写出两种方案y与x之间的函数关系式,帮助同学找到适合自己的购买方案。
①y=5x
②y=3x+4
③y=x-1
(3)在去公园路上,我们发现汽车油箱中原有汽油100升,行驶一段时间后,发现油箱的剩余油量y(单位:升)与行驶时间x(单位:时)变化满足y=-9x+100,请你根据这个关系式判断随着x的取值逐渐增大,函数y是如何变化的?
④ y=-9x+100
①y=5x
②y=3x+4
x
已知一次函数 y=(m+2) x + 3 ,当 m为何值时,y随x的增大而减小?
解:根据一次函数的性质,
当m+2<0时,y随x的增大而减小.
解不等式m+2<0,得m<-2.
所以,当m<-2时,y随x的增大而减小.
评价一:(对应目标1)
评价一
得分:
每题10分,共20分
已知一次函数y=kx-k,且y随x的增大而增大,试探索的图象经过哪几个象限?
解:
因为一次函数y=kx-k的y随x的增大而增大,所以k>0;
b=-k<0,这条直线经过第一、三、四象限.
评价二:(对应目标1)
评价一
得分:
每题10分,共20分
活动1:合作完成例题,方法尽量多
例1: (1)如果点(-2,m)和(0.5,n)都在直线y=3x+4上,至少用两种方法比较m和n的大小。
(2)(优生优培,选做)如果点(-2,m)和(0.5,n)都在直线y=kx+b(k<0)上,比较m和n的大小。
任务二:应用一次函数的性质解决问题
法一:直接代入,求出m、n的值进比较
法二:应用一次函数的增减性
法三:数形结合
1.点A(3,y1)和点B(-2,y2)都在直线y=-2x+3上,则y1和y2的大小关系是 ( )
A.y1>y2 B.y1
评价一
得分:
每题5分,共10分
B
2.(多选)下列结论中正确的有( )
A 点M(x1,y1)和N(x2,y2)都在直线y=2x-1上,若x1>x2,则y1>y2
B 直线y=-3x-4经过一、二、四象限
C 直线y=3x-1不经过第二象限
D 直线y=-x-4和直线y=x-4交点在y轴上
ACD
数形结合
分类讨论
依据解析式画图象
观察图象的升降趋势
归纳函数的增减性
从特殊
到一般
一般思路
数学思想
当堂检测得分:
每题10分,共40分
A组
1.下列函数中,y的值随x值的增大而增大的函数是( )
A.y= -2x B.y= -2x+1 C.y=x-2 D.y= -x-2
2.当1<k<2时,一次函数y=kx﹣2x+k的图象一定不过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知(x1,y1)和(x2,y2)是直线y=-3x上的两点,且x1>x2,则y1与y2大小关系是( )
A.y1>y2 B.y1
C
C
B
m=4
当堂检测得分:
每题10分,共30分
B组
5.若一次函数y=kx+3的图象经与y=-4x平行,那么这个函数的表达式为_________,y的值随x 的增大而_________。
6.如果直线y=kx+b经过一、三、四象限,那么直线y=-bx+k经过哪几个象限?
7.王老师让同学考虑一个一次函数,请小亮、小莹、大刚、王强分别对这个函数提出一个性质:
小亮:函数图象经过第二象限,不经过第三象限;
小莹:当x>0时,y<0;
大刚:y随着x的增大而减小;
王强:当x=-2时,y=3.
请画出同时适合上面四个条件的一个一次函数的图象
y=-4x+3
减小
一、二、三
当堂检测得分:
10+20分,共30分
8.对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是( )
A.0 B.2 C.3 D.4
9.己知关于x的一次函数y=mx+4m 2,
(1)若这个函数的图象经过原点,求m的值;
(2)若这个函数的图象不过第四象限,求m的取值范围;
(3)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标。
C组
B
m=
m≥
(-4,-2)
课后作业
类比一次函数性质的研究思路,研究函数y=x2+1的性质。
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
