人教版八年级下册 17.2 勾股定理的逆定理 课件(共22张PPT)
文档属性
| 名称 | 人教版八年级下册 17.2 勾股定理的逆定理 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
【大单元教学】八年级数学下册(人教版)
17 勾股定理
勾股定理的逆定理
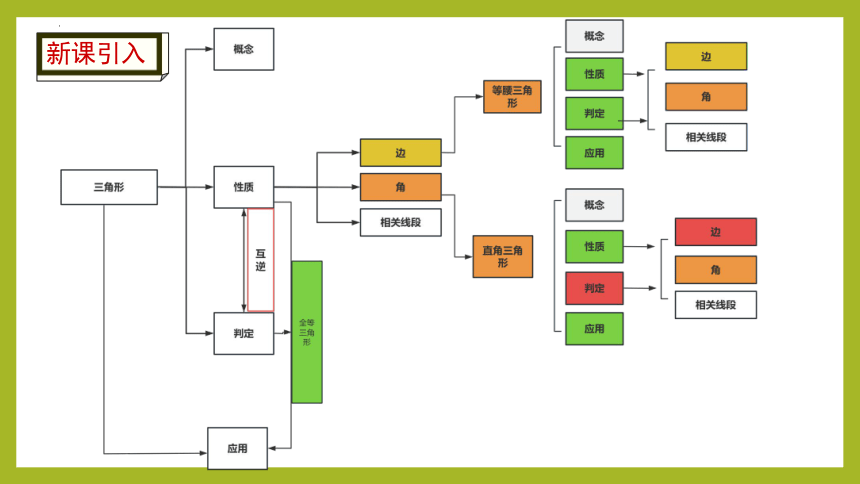
新课引入
从角的方面考虑,满足什么条件能得到直角三角形?
有两个角互余的三角形是直角三角形。
新课引入
猜想:从边的方面考虑,满足什么条件能得到直角三角形呢?
新课引入
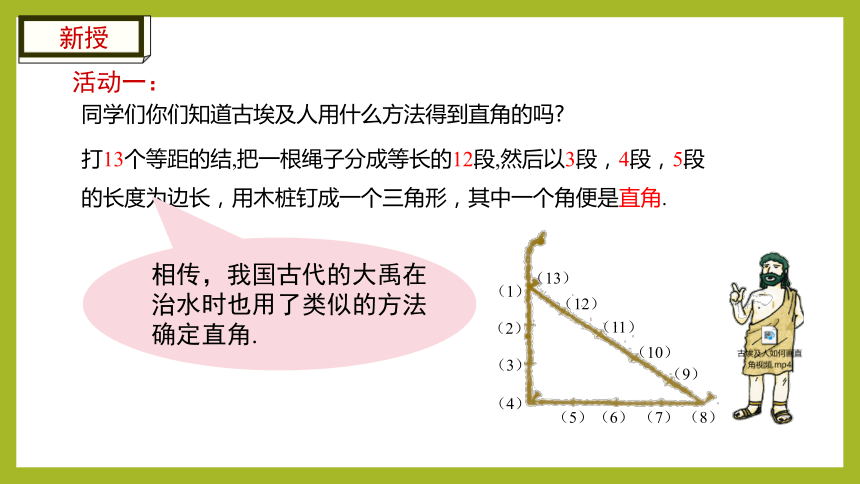
同学们你们知道古埃及人用什么方法得到直角的吗
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
相传,我国古代的大禹在治水时也用了类似的方法确定直角.
活动一:
新授
问题1 小组协作:根据古埃及人的方法将手中24cm和30cm的绳子分别围成三角形三边长为6cm 、8cm 、10cm;5cm 、12cm 、13cm的三角形,并进行测量验证它是否是直角三角形?思考它们的边之间有什么数量关系?
新授 活动一:
是直角三角形,
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
问题2 通过刚刚动手测量的结果,我们猜想如果三角形ABC三边长为a,b,c,边满足什么条件能判定此三角形是直角三角形?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
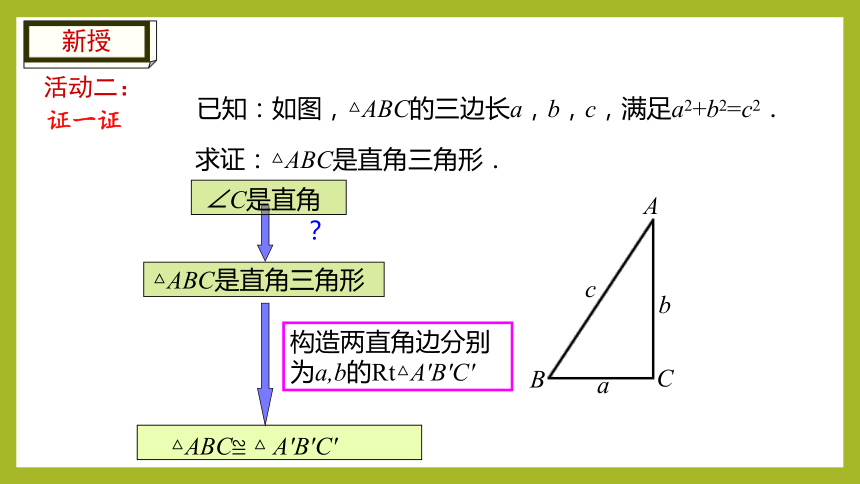
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
证一证
活动二:
新授
A
B
C
a
b
c
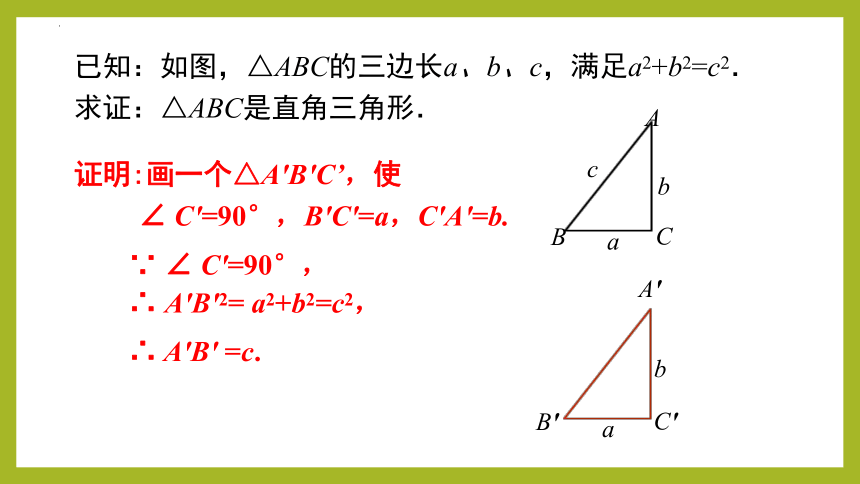
已知:如图,△ABC的三边长a、b、c,满足a2+b2=c2.
求证:△ABC是直角三角形.
证明:画一个△A'B'C’,使
∠ C'=90°,B'C'=a,C'A'=b.
∵ ∠ C'=90°,
∴ A'B'2= a2+b2=c2,
∴ A'B' =c.
A'
B'
C'
a
A
B
C
a
b
c
A'
B'
C'
a
c
∴ △ ABC ≌△ A'B'C'(SSS).
∴ ∠C=∠C'=90°.
BC=a=B'C’,
CA=b=C'A’,
AB=c=A'B'.
在△ABC和△A'B'C'中
勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
特别说明:
活动三:
归纳总结
上述操作, 你得到的结论是什么?它能不能成为直角三角 形的判定方法? 类比勾股定理,你能不能说出它的几何语言?
新授
下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=2.5 , b=6 ,c=6.5;
解:(1)∵2.52+62=42.25,6.52=42.25,∴2.52+62=6.52,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
(2) a=13 ,b=14 ,c=15.
(2)∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,∴这个三角形不是直角三角形.
根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
归纳
跟练
命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
命题2 如果三角形ABC的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
我们把像这样,题设和结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
新授
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.
勾股定理与勾股定理的逆定理为互逆定理.
1.说出下列命题的逆命题,这些逆命题成立吗?
(1)全等三角形的对应角相等;
对应角相等的三角形全等 .
(2)在角的内部,到角的两边距离相等的点在角的平分
线上.
在角平分线上的点到角的两边距离相等.
不成立
成立
跟练
应用基础篇
1.(1)规划耕地后, 小明家被分得了如下图,所示
的田地。为了更精准的准备物资,小明需要知道这
块耕地的面积。你能帮他解决问题吗?
(2)小明家还有一块不规则的田地,其边长如图
所示, ∠A=90°。计算该田地的面积。
定义
性质
角:
边:(勾股定理逆定理)
判定
归纳
A
B
C
a
b
c
应用
角:
边:(勾股定理) a2+b2=c2
猜想,验证,归纳
勾股定理的逆定理
知识回顾
探究思路
猜想,验证,归纳
1.如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形。
2.原命题,逆命题,互逆命题,互逆定理。
1.★如右图,现有一块废铁板, AC =24cm,AB =18cm,现有一把长为30cm 的刻度尺,你能否检测 AB 是否垂直于 AC?说出你的设计方案。
2 . ★★如右图,一块形如四边形 ABCD 的草地中, AB =3m,BC = 4m ,CD =12m,DA =13m,且∠ABC =90°, 要以 AC、CD、DA 为 边制作围栏,问围栏长多少米,草地面积多大?
课后巩固
3.★★★今年第 6 号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力。如图 7 台风“烟花” 中心沿东西方向 AB 由 A 向 B 移动,已知点 C 为一海港,且点 C 与直线 AB 上的两点 A、B 的距离分别为 AC =600km ,BC =800km,又 AB =1000km,以台风中心为圆心, 周围 500km 以内为受影响区域。
学生自评表 重点知识掌握情况(满分30分) l 理解勾股定理逆定理的证明过程(10分)
l 运用勾股定理逆定理解决问题 (10分)
l 理解互逆命题及互逆定理定义(10分)
课堂活动参与情况(满分40分) l 参与打绳结、画图等活动的积极性及猜想验证的有效性(10分)
l 在推理证明过程中展现的逻辑思维和严谨性(10分)
l 能否有效运用数形结合思想解决问题(10分)
l 在概念学习和逻辑构建方面的表现(10分)
自我感受满意程度(满分30分) l 感觉自己态度是否积极,能否保持高度专注(10分)
l 感觉自己独立思考与探索精神怎样(10分)
l 学习兴趣是否浓厚,能否将所学知识应用于实际问题(10分)
给老师建议: 总分:
谢谢大家
【大单元教学】八年级数学下册(人教版)
17 勾股定理
勾股定理的逆定理
新课引入
从角的方面考虑,满足什么条件能得到直角三角形?
有两个角互余的三角形是直角三角形。
新课引入
猜想:从边的方面考虑,满足什么条件能得到直角三角形呢?
新课引入
同学们你们知道古埃及人用什么方法得到直角的吗
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
打13个等距的结,把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
相传,我国古代的大禹在治水时也用了类似的方法确定直角.
活动一:
新授
问题1 小组协作:根据古埃及人的方法将手中24cm和30cm的绳子分别围成三角形三边长为6cm 、8cm 、10cm;5cm 、12cm 、13cm的三角形,并进行测量验证它是否是直角三角形?思考它们的边之间有什么数量关系?
新授 活动一:
是直角三角形,
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
问题2 通过刚刚动手测量的结果,我们猜想如果三角形ABC三边长为a,b,c,边满足什么条件能判定此三角形是直角三角形?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
△ABC≌ △ A′B′C′
?
∠C是直角
△ABC是直角三角形
A
B
C
a
b
c
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
构造两直角边分别为a,b的Rt△A′B′C′
证一证
活动二:
新授
A
B
C
a
b
c
已知:如图,△ABC的三边长a、b、c,满足a2+b2=c2.
求证:△ABC是直角三角形.
证明:画一个△A'B'C’,使
∠ C'=90°,B'C'=a,C'A'=b.
∵ ∠ C'=90°,
∴ A'B'2= a2+b2=c2,
∴ A'B' =c.
A'
B'
C'
a
A
B
C
a
b
c
A'
B'
C'
a
c
∴ △ ABC ≌△ A'B'C'(SSS).
∴ ∠C=∠C'=90°.
BC=a=B'C’,
CA=b=C'A’,
AB=c=A'B'.
在△ABC和△A'B'C'中
勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
特别说明:
活动三:
归纳总结
上述操作, 你得到的结论是什么?它能不能成为直角三角 形的判定方法? 类比勾股定理,你能不能说出它的几何语言?
新授
下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=2.5 , b=6 ,c=6.5;
解:(1)∵2.52+62=42.25,6.52=42.25,∴2.52+62=6.52,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
(2) a=13 ,b=14 ,c=15.
(2)∵132+142=365,152=225,
∴132+142≠152,不符合勾股定理的逆定理,∴这个三角形不是直角三角形.
根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
归纳
跟练
命题1 如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
命题2 如果三角形ABC的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
我们把像这样,题设和结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
新授
一般地,原命题成立时,它的逆命题既可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.
勾股定理与勾股定理的逆定理为互逆定理.
1.说出下列命题的逆命题,这些逆命题成立吗?
(1)全等三角形的对应角相等;
对应角相等的三角形全等 .
(2)在角的内部,到角的两边距离相等的点在角的平分
线上.
在角平分线上的点到角的两边距离相等.
不成立
成立
跟练
应用基础篇
1.(1)规划耕地后, 小明家被分得了如下图,所示
的田地。为了更精准的准备物资,小明需要知道这
块耕地的面积。你能帮他解决问题吗?
(2)小明家还有一块不规则的田地,其边长如图
所示, ∠A=90°。计算该田地的面积。
定义
性质
角:
边:(勾股定理逆定理)
判定
归纳
A
B
C
a
b
c
应用
角:
边:(勾股定理) a2+b2=c2
猜想,验证,归纳
勾股定理的逆定理
知识回顾
探究思路
猜想,验证,归纳
1.如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形。
2.原命题,逆命题,互逆命题,互逆定理。
1.★如右图,现有一块废铁板, AC =24cm,AB =18cm,现有一把长为30cm 的刻度尺,你能否检测 AB 是否垂直于 AC?说出你的设计方案。
2 . ★★如右图,一块形如四边形 ABCD 的草地中, AB =3m,BC = 4m ,CD =12m,DA =13m,且∠ABC =90°, 要以 AC、CD、DA 为 边制作围栏,问围栏长多少米,草地面积多大?
课后巩固
3.★★★今年第 6 号台风“烟花”登录我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力。如图 7 台风“烟花” 中心沿东西方向 AB 由 A 向 B 移动,已知点 C 为一海港,且点 C 与直线 AB 上的两点 A、B 的距离分别为 AC =600km ,BC =800km,又 AB =1000km,以台风中心为圆心, 周围 500km 以内为受影响区域。
学生自评表 重点知识掌握情况(满分30分) l 理解勾股定理逆定理的证明过程(10分)
l 运用勾股定理逆定理解决问题 (10分)
l 理解互逆命题及互逆定理定义(10分)
课堂活动参与情况(满分40分) l 参与打绳结、画图等活动的积极性及猜想验证的有效性(10分)
l 在推理证明过程中展现的逻辑思维和严谨性(10分)
l 能否有效运用数形结合思想解决问题(10分)
l 在概念学习和逻辑构建方面的表现(10分)
自我感受满意程度(满分30分) l 感觉自己态度是否积极,能否保持高度专注(10分)
l 感觉自己独立思考与探索精神怎样(10分)
l 学习兴趣是否浓厚,能否将所学知识应用于实际问题(10分)
给老师建议: 总分:
谢谢大家
