青岛版九年级上册 2.5解直角三角形的应用 课件(共20张PPT)
文档属性
| 名称 | 青岛版九年级上册 2.5解直角三角形的应用 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 901.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 08:36:57 | ||
图片预览






文档简介
(共20张PPT)
九年级上册第二章
2.5 解直角三角形的应用
视角问题
情境导入
有一位小朋友,正抬头仰望高高
飘扬的五星红旗,这时她陷入了沉
思:我怎样才能测出旗杆的高度?
如果给你足够的工具,聪明的你会
用所学知识测出旗杆的高度吗?
学习目标
1.通过概念的学习,了解仰角、俯角的意义,能根据实际问题转化成数学模型.
2.通过例题的学习,会用解直角三角形的有关知识解某些简单的实际问题.
3.通过本节课,进一步体会转化思想和方程思想.
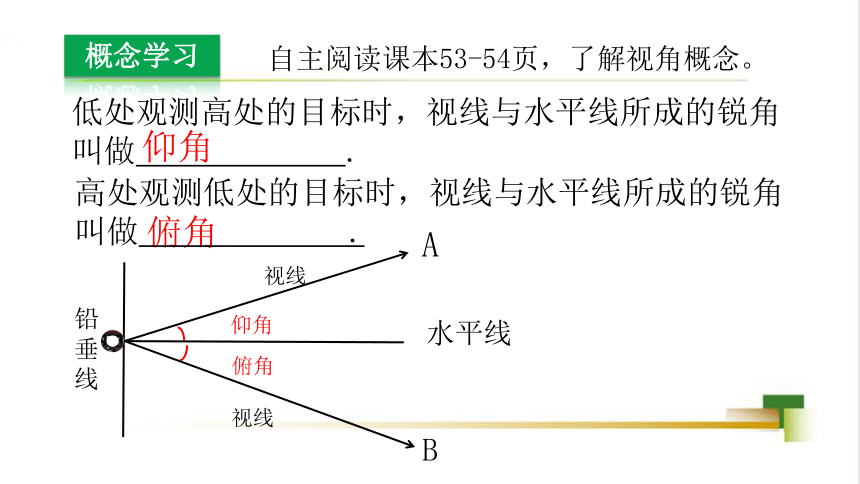
概念学习
低处观测高处的目标时,视线与水平线所成的锐角叫做 .
自主阅读课本53-54页,了解视角概念。
仰角
俯角
铅垂线
水平线
A
视线
仰角
高处观测低处的目标时,视线与水平线所成的锐角叫做 .
俯角
B
视线
概念学习
关键词解读:仰角是视线在水平线上方的夹角;俯角是视线在水平线下方的夹角.
(2019河北)如图,从点C观测点D的仰角是( ).
(变式)从点D观测点A的俯角是( ).
水平地面
A
C
D
E
B
F
∠DCE
∠FDA
典例引领
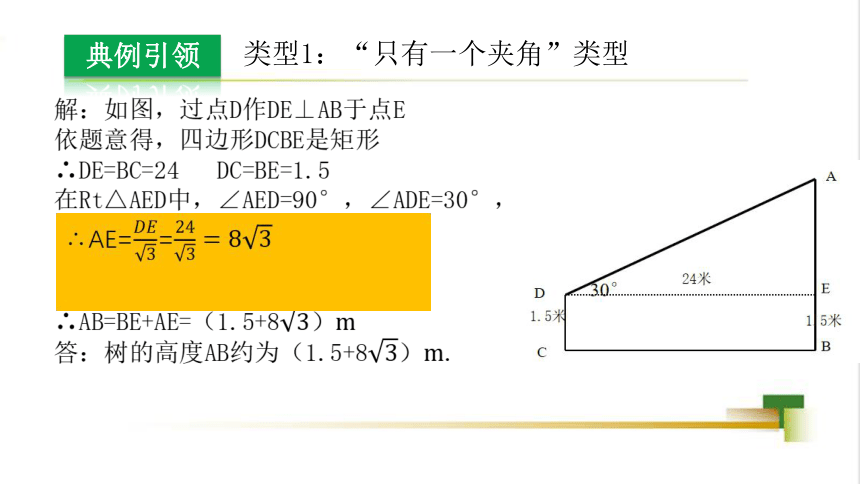
【例1】一位同学站在离旗杆24米处,测得旗杆顶端的仰角恰为30°,若两眼离地面1.5米,则旗杆的高度是否可求?若可求,求出旗杆的高,若不可求,说明理由.(结果保留根号)
类型1:“只有一个夹角”类型
1.构
2.找
3.解
转化思想
在RT△ADE中,∠AED=90°,∠ADE=30°,DE=24m
tan30°=即AE=DEtan30°=24
∴AE==
典例引领
类型1:“只有一个夹角”类型
解:如图,过点D作DE⊥AB于点E
依题意得,四边形DCBE是矩形
∴DE=BC=24 DC=BE=1.5
在Rt△AED中,∠AED=90°,∠ADE=30°,∵tan30°=
∴AE=DE·tan30°=24×=8
∴AB=BE+AE=(1.5+8)m
答:树的高度AB约为(1.5+8)m.
∴AE==
典例引领
类型2:“两个夹角”类型(同一地点看不同点)
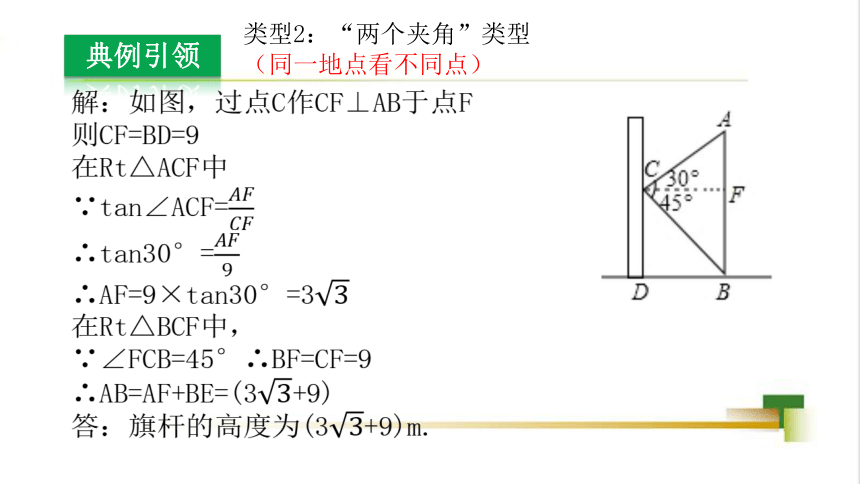
【例2】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°. 已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).
转化思想
典例引领
解:如图,过点C作CF⊥AB于点F
则CF=BD=9
在Rt△ACF中
∵tan∠ACF=
∴tan30°=
∴AF=9×tan30°=3
在Rt△BCF中,∵∠FCB=45°∴BF=CF=9
∴AB=AF+BE=(3+9)
答:旗杆的高度为(3+9)m.
类型2:“两个夹角”类型(同一地点看不同点)
变式训练
【变式】如图,要测量铁塔的高AB,在地面上选取一点C,在AC两点间选取一点D,测得CD=14m,在C,D两点处分别用测角仪测得铁塔顶端B的仰角α=30°和β=45°.测角仪支架的高为1.2m,求铁塔的高(结果保留根号).
转化思想
方程思想
类型2:“两个夹角”类型
(不同地点看同一地点)
解:由题意可知:AA1=CC1=DD1=1.2m,CD=C1D1=14m。
设A1B= x m,
∴AB=AA1+A1B=7(+1)+1.2=7+8.2≈20.3(m)
∴铁塔的高约为20.3m。
变式训练
类型2:“两个夹角”类型(不同地点看同一地点)
归纳总结
这节课你学到了什么?自我反思后,小组内交流.
课堂小结
达标检测
1.如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米.
A. 50sin35°
B. 50cos35°
C.
D.
C
达标检测
2.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( ).
A. 8(3-)m
B. 8(3)m
C. 6(3-)m
D. 6(3+)m
A
达标检测
3.如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线AB长为100m,从A处看风筝的仰角为30°,小明的父母从C处看风筝的仰角为50°.
(1)风筝离地面多少m?
D
解(1)如图,过B作BD⊥AC
在Rt△ABD中,
∵sinA==
∴BD==50m
∴风筝离地面50m
达标检测
3.如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线AB长为100m,从A处看风筝的仰角为30°,小明的父母从C处看风筝的仰角为50°.
(1)风筝离地面多少m?
(2)AC相距多少m?(结果保留小数点后一位,参考数据:sin30°=0.5,cos30°=0.866,tan30°=0.577,sin50°=0.776,cos50°=0.643,tan50°=1.192)
D
50m
达标检测
D
(2)在Rt△ABD中,
∵cosA=0.866
∴AD==86.6m
在Rt△CBD中,
∵tanC 1.192
∴CD=41.95m
∴AC=AD+CD=128.55128.6m
∴AC相距128.6m.
要求:
1.完成【基础达标作业】和【综合提升作业】;
2.学有余力的同学完成【核心素养作业】.
课后作业
再见
九年级上册第二章
2.5 解直角三角形的应用
视角问题
情境导入
有一位小朋友,正抬头仰望高高
飘扬的五星红旗,这时她陷入了沉
思:我怎样才能测出旗杆的高度?
如果给你足够的工具,聪明的你会
用所学知识测出旗杆的高度吗?
学习目标
1.通过概念的学习,了解仰角、俯角的意义,能根据实际问题转化成数学模型.
2.通过例题的学习,会用解直角三角形的有关知识解某些简单的实际问题.
3.通过本节课,进一步体会转化思想和方程思想.
概念学习
低处观测高处的目标时,视线与水平线所成的锐角叫做 .
自主阅读课本53-54页,了解视角概念。
仰角
俯角
铅垂线
水平线
A
视线
仰角
高处观测低处的目标时,视线与水平线所成的锐角叫做 .
俯角
B
视线
概念学习
关键词解读:仰角是视线在水平线上方的夹角;俯角是视线在水平线下方的夹角.
(2019河北)如图,从点C观测点D的仰角是( ).
(变式)从点D观测点A的俯角是( ).
水平地面
A
C
D
E
B
F
∠DCE
∠FDA
典例引领
【例1】一位同学站在离旗杆24米处,测得旗杆顶端的仰角恰为30°,若两眼离地面1.5米,则旗杆的高度是否可求?若可求,求出旗杆的高,若不可求,说明理由.(结果保留根号)
类型1:“只有一个夹角”类型
1.构
2.找
3.解
转化思想
在RT△ADE中,∠AED=90°,∠ADE=30°,DE=24m
tan30°=即AE=DEtan30°=24
∴AE==
典例引领
类型1:“只有一个夹角”类型
解:如图,过点D作DE⊥AB于点E
依题意得,四边形DCBE是矩形
∴DE=BC=24 DC=BE=1.5
在Rt△AED中,∠AED=90°,∠ADE=30°,∵tan30°=
∴AE=DE·tan30°=24×=8
∴AB=BE+AE=(1.5+8)m
答:树的高度AB约为(1.5+8)m.
∴AE==
典例引领
类型2:“两个夹角”类型(同一地点看不同点)
【例2】如图,在数学活动课上,小丽为了测量校园内旗杆AB的高度,站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°. 已知旗杆与教学楼的距离BD=9m,请你帮她求出旗杆的高度(结果保留根号).
转化思想
典例引领
解:如图,过点C作CF⊥AB于点F
则CF=BD=9
在Rt△ACF中
∵tan∠ACF=
∴tan30°=
∴AF=9×tan30°=3
在Rt△BCF中,∵∠FCB=45°∴BF=CF=9
∴AB=AF+BE=(3+9)
答:旗杆的高度为(3+9)m.
类型2:“两个夹角”类型(同一地点看不同点)
变式训练
【变式】如图,要测量铁塔的高AB,在地面上选取一点C,在AC两点间选取一点D,测得CD=14m,在C,D两点处分别用测角仪测得铁塔顶端B的仰角α=30°和β=45°.测角仪支架的高为1.2m,求铁塔的高(结果保留根号).
转化思想
方程思想
类型2:“两个夹角”类型
(不同地点看同一地点)
解:由题意可知:AA1=CC1=DD1=1.2m,CD=C1D1=14m。
设A1B= x m,
∴AB=AA1+A1B=7(+1)+1.2=7+8.2≈20.3(m)
∴铁塔的高约为20.3m。
变式训练
类型2:“两个夹角”类型(不同地点看同一地点)
归纳总结
这节课你学到了什么?自我反思后,小组内交流.
课堂小结
达标检测
1.如图,AB表示一条跳台滑雪赛道,在点A处测得起点B的仰角为35°,底端点C与顶端点B的距离为50米,则赛道AB的长度为( )米.
A. 50sin35°
B. 50cos35°
C.
D.
C
达标检测
2.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16m,则这棵树CD的高度是( ).
A. 8(3-)m
B. 8(3)m
C. 6(3-)m
D. 6(3+)m
A
达标检测
3.如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线AB长为100m,从A处看风筝的仰角为30°,小明的父母从C处看风筝的仰角为50°.
(1)风筝离地面多少m?
D
解(1)如图,过B作BD⊥AC
在Rt△ABD中,
∵sinA==
∴BD==50m
∴风筝离地面50m
达标检测
3.如图,小明同学在民族广场A处放风筝,风筝位于B处,风筝线AB长为100m,从A处看风筝的仰角为30°,小明的父母从C处看风筝的仰角为50°.
(1)风筝离地面多少m?
(2)AC相距多少m?(结果保留小数点后一位,参考数据:sin30°=0.5,cos30°=0.866,tan30°=0.577,sin50°=0.776,cos50°=0.643,tan50°=1.192)
D
50m
达标检测
D
(2)在Rt△ABD中,
∵cosA=0.866
∴AD==86.6m
在Rt△CBD中,
∵tanC 1.192
∴CD=41.95m
∴AC=AD+CD=128.55128.6m
∴AC相距128.6m.
要求:
1.完成【基础达标作业】和【综合提升作业】;
2.学有余力的同学完成【核心素养作业】.
课后作业
再见
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
