2.5《二次函数与一元二次方程》第1课时 课件
文档属性
| 名称 | 2.5《二次函数与一元二次方程》第1课时 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 15:32:24 | ||
图片预览






文档简介
(共18张PPT)
2.5 二次函数
与
一元二次方程
---李晶
北师大版九年级数学下册第二章
学习环节:
一、新知探究1:
二、及时巩固;
三、新知探究2;
四、及时巩固;
五、课堂小结;
六、闯关提升。
新知探究1
一元二次方程ax2+bx+c=0的两个根x1、x2, 与抛物线y=ax2+bx+c与x轴的两个交点坐标之间的关系?
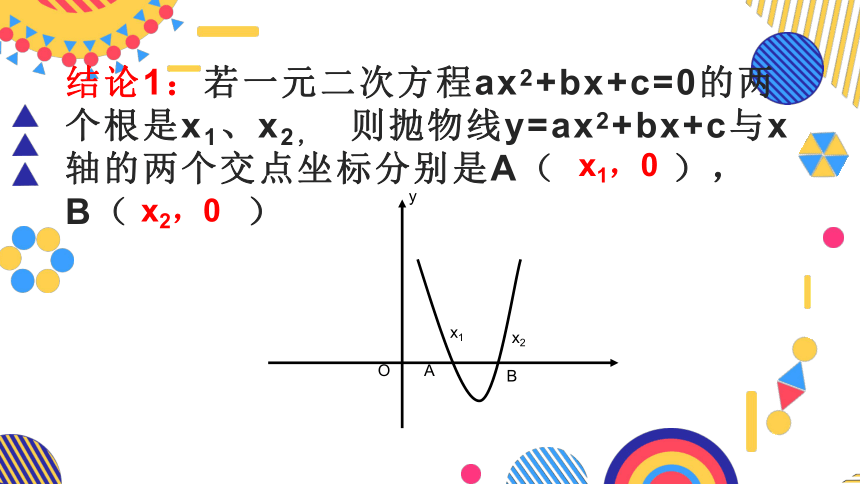
结论1:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ),
B( )
x1,0
x2,0
O
A
B
x1
x2
y
及时巩固1
1、求二次函数 的图像与x轴的交点坐标
2、二次函数y=ax2+bx+c与
x轴的两个交点坐标如图所示,
则ax2+bx+c=0的两个根是?
O
A
B
2
4
y
新知探究2
抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?
结论2:
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、 b2-4ac >0 一元二次方程ax2+bx+c=0
有两个不等的实数根
与x轴有两个交点——相交。
抛物线y=ax2+bx+c
2、 b2-4ac =0 一元二次方程ax2+bx+c=0
有两个相等的实数根
与x轴有唯一公共点——相切(顶点)。
抛物线y=ax2+bx+c
3、 b2-4ac <0 一元二次方程ax2+bx+c=0
没有实数根
与x轴没有公共点——相离。
及时巩固2
二次函数 的图像与x轴有几个交点?
课堂小结1若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ),
B( )
x1,0
x2,0
O
A
B
x1
x2
y
2:
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、 b2-4ac >0 一元二次方程ax2+bx+c=0
有两个不等的实数根
与x轴有两个交点——相交。
抛物线y=ax2+bx+c
2、 b2-4ac =0 一元二次方程ax2+bx+c=0
有两个相等的实数根
与x轴有唯一公共点——相切(顶点)。
抛物线y=ax2+bx+c
3、 b2-4ac <0 一元二次方程ax2+bx+c=0
没有实数根
与x轴没有公共点——相离。
闯关提升
初级闯关 1、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。(1)y=6x2-2x+1
(2)y=-15x2+14x+8
(3)y=x2-4x+4
不相交
相交
(相交)
中级闯关 已知二次函数 的图像与x轴有两个交点,求m的取值范围
终级闯关 已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值,并求出交点坐标。
(2)若抛物线与直线y=-4只有一个交点,求 m的值,并求出交点坐标。
(3)y=x+2m只有一个交点,求m的值,并求出交点坐标。
终级闯关 已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值,并求出交点坐标。
终级闯关 已知抛物线y=x2+2x+m+1。
(2)若抛物线与直线y=-4只有一个交点,求 m的值,并求出交点坐标。
终级闯关 已知抛物线y=x2+2x+m+1。
(3)y=x+2m只有一个交点,求m的值,并求出交点坐标。
极限挑战 如果二次函数y=x2-kx-1+k与x轴两个交点为A、B,设此抛物线与y轴的交点为C,(1)当k=6时,求S△ABC .
(2)当S△ABC=21时,求 k的值。
10
-5或8
详细答案见下页
2.5 二次函数
与
一元二次方程
---李晶
北师大版九年级数学下册第二章
学习环节:
一、新知探究1:
二、及时巩固;
三、新知探究2;
四、及时巩固;
五、课堂小结;
六、闯关提升。
新知探究1
一元二次方程ax2+bx+c=0的两个根x1、x2, 与抛物线y=ax2+bx+c与x轴的两个交点坐标之间的关系?
结论1:若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ),
B( )
x1,0
x2,0
O
A
B
x1
x2
y
及时巩固1
1、求二次函数 的图像与x轴的交点坐标
2、二次函数y=ax2+bx+c与
x轴的两个交点坐标如图所示,
则ax2+bx+c=0的两个根是?
O
A
B
2
4
y
新知探究2
抛物线与X 轴的交点个数能不能用一元二次方程的知识来说明呢?
结论2:
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、 b2-4ac >0 一元二次方程ax2+bx+c=0
有两个不等的实数根
与x轴有两个交点——相交。
抛物线y=ax2+bx+c
2、 b2-4ac =0 一元二次方程ax2+bx+c=0
有两个相等的实数根
与x轴有唯一公共点——相切(顶点)。
抛物线y=ax2+bx+c
3、 b2-4ac <0 一元二次方程ax2+bx+c=0
没有实数根
与x轴没有公共点——相离。
及时巩固2
二次函数 的图像与x轴有几个交点?
课堂小结1若一元二次方程ax2+bx+c=0的两个根是x1、x2, 则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A( ),
B( )
x1,0
x2,0
O
A
B
x1
x2
y
2:
抛物线y=ax2+bx+c
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
1、 b2-4ac >0 一元二次方程ax2+bx+c=0
有两个不等的实数根
与x轴有两个交点——相交。
抛物线y=ax2+bx+c
2、 b2-4ac =0 一元二次方程ax2+bx+c=0
有两个相等的实数根
与x轴有唯一公共点——相切(顶点)。
抛物线y=ax2+bx+c
3、 b2-4ac <0 一元二次方程ax2+bx+c=0
没有实数根
与x轴没有公共点——相离。
闯关提升
初级闯关 1、判断下列各抛物线是否与x轴相交,如果相交,求出交点的坐标。(1)y=6x2-2x+1
(2)y=-15x2+14x+8
(3)y=x2-4x+4
不相交
相交
(相交)
中级闯关 已知二次函数 的图像与x轴有两个交点,求m的取值范围
终级闯关 已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值,并求出交点坐标。
(2)若抛物线与直线y=-4只有一个交点,求 m的值,并求出交点坐标。
(3)y=x+2m只有一个交点,求m的值,并求出交点坐标。
终级闯关 已知抛物线y=x2+2x+m+1。
(1)若抛物线与x轴只有一个交点,求m的值,并求出交点坐标。
终级闯关 已知抛物线y=x2+2x+m+1。
(2)若抛物线与直线y=-4只有一个交点,求 m的值,并求出交点坐标。
终级闯关 已知抛物线y=x2+2x+m+1。
(3)y=x+2m只有一个交点,求m的值,并求出交点坐标。
极限挑战 如果二次函数y=x2-kx-1+k与x轴两个交点为A、B,设此抛物线与y轴的交点为C,(1)当k=6时,求S△ABC .
(2)当S△ABC=21时,求 k的值。
10
-5或8
详细答案见下页
