3.2《圆的对称性》戚纪
图片预览






文档简介
(共19张PPT)
§3.2 圆的对称性
北师大版 数学 九年级下册
深圳市罗湖区翠园初级中学 戚纪
学习目标:
了解圆的轴对称性和中心对称性及相关性质。
掌握圆心角、弧、弦之间相等关系定理及应用。
知识点1:圆的对称性
什么是轴对称图形?
什么叫中心对称图形?
答:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。
答:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
知识点1:圆的对称性
什么是轴对称图形?
什么叫中心对称图形?
答:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。
答:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
知识点1:圆的对称性
1、圆是轴对称图形吗?如果是,它的对称轴是什么?
2、圆是中心对称图形吗?如果是,它的对称中心是什么?
圆
中心对称
轴对称
旋转不变性
【想一想】
一个圆绕着它的圆心旋转任意一个角度,还能与原来的图形重合吗?
对称轴是任意一条经过圆心的直线。
对称中心是圆心。
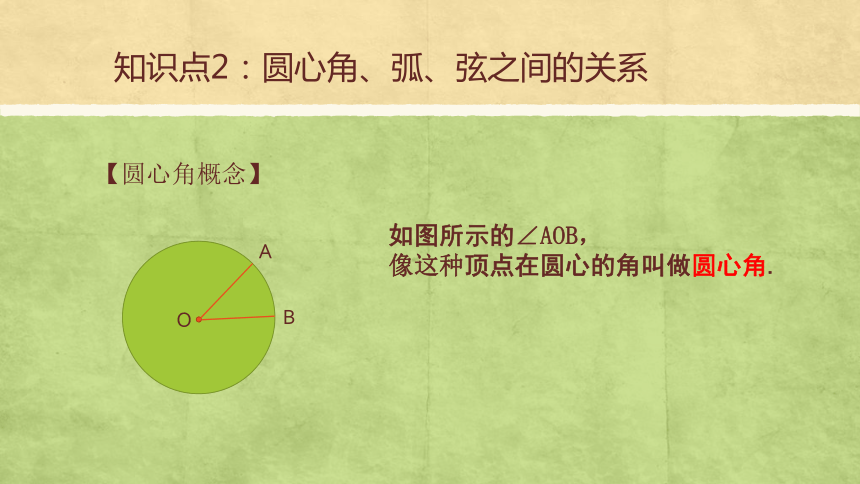
知识点2:圆心角、弧、弦之间的关系
【圆心角概念】
A
B
O
如图所示的∠AOB,
像这种顶点在圆心的角叫做圆心角.
A
B
O
A
B
O
A
B
O
A
B
O
①
②
③
④
【辨一辨】判别上图中的角是不是圆心角?
√
知识点2:圆心角、弧、弦之间的关系
·
A
B
【想一想】如图,在等圆⊙O和⊙O‘中,分别作相等的圆心角∠AOB和∠A’O’B’ ,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得OA与O‘A’重合。你能发现哪些等量关系?说一说你的理由。
O
·
A'
B'
O'
等量关系:
∠AOB=∠A’O’B’(已知)
OA=OB=O’A’=O’B’(半径)
∠A= ∠B=∠A’ =∠B’
AB=A’B’
知识点2:圆心角、弧、弦之间的关系
·
A
B
【想一想】如图,在等圆⊙O和⊙O‘中,分别作相等的圆心角∠AOB和∠A’O’B’ ,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得OA与O‘A’重合。你能发现哪些等量关系?说一说你的理由。
O
·
A'
B'
O'
知识点2:圆心角、弧、弦之间的关系
·
A
B
A'
B'
【想一想】如图,在等圆⊙O和⊙O‘中,分别作相等的圆心角∠AOB和∠A’O’B’ ,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得OA与O‘A’重合。你能发现哪些等量关系?说一说你的理由。
O
∵半径OA与O’A’重合,∠AOB=∠A’O’B’
∴半径OB与O’B’重合。
∵点A与点A’重合,点B与点B’重合,
∴ AB与A’B’重合 ,弦AB与弦A’B’重合。
⌒
⌒
∴AB=A’B’ , AB=A’B’ 。
⌒
⌒
(O′)
知识点2:圆心角、弧、弦之间的关系
在 等圆中,相等的圆心角所对的弧相等,所对的弦相等.
同圆或
知识点2:圆心角定理
几何语言:
∴ AB=A’B’ , AB=A’B’
⌒
⌒
∵ ∠AOB=∠A’O’B’
·
A
B
O
·
A'
B'
O'
几何画板中的圆心角、弧、弦之间的关系
等对等定理
O
A
B
C
D
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
(1)∵ ∠AOB=∠COD
几何语言:
O
A
B
C
D
∴ AB=CD , AB=CD
⌒
⌒
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
(2)∵ AB=CD
∴ AB=CD ,∠AOB=∠COD
⌒
⌒
(3)∵ AB=CD
⌒
⌒
∴ AB=CD ,∠AOB=∠COD
等对等定理
如图,在⊙O中,
例:如图,AB、DE是⊙O的直径,C是⊙O上的一点,且AD=CE。BE与CE的大小有什么关系?为什么?
⌒
⌒
B
E
O
D
A
C
BE=CE;理由是:
∵ ∠AOD=∠BOE
∴ AD=BE
⌒
⌒
又∵ AD=CE
⌒
⌒
∴ BE=CE
⌒
⌒
∴ BE=CE
答:
练习1:如图,A、B、C、D是⊙O上的四点, AB=DC ,△ABC与△DCB全等吗?为什么?
·
O
A
B
C
D
答:
全等;理由是:
∵ AB=DC
∴ AC=DB
又∵AB=DC,BC=CB
∴ AB=DC
⌒
⌒
⌒
∴ AB+BC=DC+BC
⌒
⌒
⌒
∴ AC=DB
⌒
⌒
∴ △ABC≌△DCB(SSS)
+
·
O
D
C
A
B
F
E
练习2:如图,在⊙O中, AB,CD是两条弦 ,OE⊥AB,OF⊥CD,垂足分别为E,F。
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系?AB与CD的大小有什么关系? ∠AOB=∠COD呢?为什么?
⌒
⌒
解: (1)OE=OF;理由是:
在⊙O中,OA=OB=OC=OD
∵ OE⊥AB,OF⊥CD
∴ ∠AEO=∠CFO=90°,∠AOE=∠BOE= ∠AOB,
∠COF=∠DOF= ∠COD
∵ ∠AOB=∠COD
∴ ∠AOE= ∠COF
又∵ ∠AEO=∠CFO,OA=OC
∴△AOE≌△COF(AAS)
∴OE=OF
从圆心到弦的距离叫弦心距。
·
O
D
C
A
B
F
E
练习2:如图,在⊙O中, AB,CD是两条弦 ,OE⊥AB,OF⊥CD,垂足分别为E,F。
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系?AB与CD的大小有什么关系? ∠AOB=∠COD呢?为什么?
⌒
⌒
(2)∵ OE⊥AB,OF⊥CD
∴ ∠AEO=∠CFO=90°
∵ OE=OF,OA=OC
∴Rt△AOE≌Rt△COF(HL)
∴AE=CF
同理得,Rt△BOE≌Rt△DOF
∴BE=DF
∴AE+ BE =CF+DF
∴AB=CD
∴AB=CD,∠AOB=∠COD
⌒
⌒
≌
≌
≌
≌
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
1、圆的特殊对称性。
2、在同圆或等圆中,圆心 角、弧、弦之间的关系。
小结:
·
§3.2 圆的对称性
北师大版 数学 九年级下册
深圳市罗湖区翠园初级中学 戚纪
学习目标:
了解圆的轴对称性和中心对称性及相关性质。
掌握圆心角、弧、弦之间相等关系定理及应用。
知识点1:圆的对称性
什么是轴对称图形?
什么叫中心对称图形?
答:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。
答:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
知识点1:圆的对称性
什么是轴对称图形?
什么叫中心对称图形?
答:如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形。
答:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形。
知识点1:圆的对称性
1、圆是轴对称图形吗?如果是,它的对称轴是什么?
2、圆是中心对称图形吗?如果是,它的对称中心是什么?
圆
中心对称
轴对称
旋转不变性
【想一想】
一个圆绕着它的圆心旋转任意一个角度,还能与原来的图形重合吗?
对称轴是任意一条经过圆心的直线。
对称中心是圆心。
知识点2:圆心角、弧、弦之间的关系
【圆心角概念】
A
B
O
如图所示的∠AOB,
像这种顶点在圆心的角叫做圆心角.
A
B
O
A
B
O
A
B
O
A
B
O
①
②
③
④
【辨一辨】判别上图中的角是不是圆心角?
√
知识点2:圆心角、弧、弦之间的关系
·
A
B
【想一想】如图,在等圆⊙O和⊙O‘中,分别作相等的圆心角∠AOB和∠A’O’B’ ,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得OA与O‘A’重合。你能发现哪些等量关系?说一说你的理由。
O
·
A'
B'
O'
等量关系:
∠AOB=∠A’O’B’(已知)
OA=OB=O’A’=O’B’(半径)
∠A= ∠B=∠A’ =∠B’
AB=A’B’
知识点2:圆心角、弧、弦之间的关系
·
A
B
【想一想】如图,在等圆⊙O和⊙O‘中,分别作相等的圆心角∠AOB和∠A’O’B’ ,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得OA与O‘A’重合。你能发现哪些等量关系?说一说你的理由。
O
·
A'
B'
O'
知识点2:圆心角、弧、弦之间的关系
·
A
B
A'
B'
【想一想】如图,在等圆⊙O和⊙O‘中,分别作相等的圆心角∠AOB和∠A’O’B’ ,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得OA与O‘A’重合。你能发现哪些等量关系?说一说你的理由。
O
∵半径OA与O’A’重合,∠AOB=∠A’O’B’
∴半径OB与O’B’重合。
∵点A与点A’重合,点B与点B’重合,
∴ AB与A’B’重合 ,弦AB与弦A’B’重合。
⌒
⌒
∴AB=A’B’ , AB=A’B’ 。
⌒
⌒
(O′)
知识点2:圆心角、弧、弦之间的关系
在 等圆中,相等的圆心角所对的弧相等,所对的弦相等.
同圆或
知识点2:圆心角定理
几何语言:
∴ AB=A’B’ , AB=A’B’
⌒
⌒
∵ ∠AOB=∠A’O’B’
·
A
B
O
·
A'
B'
O'
几何画板中的圆心角、弧、弦之间的关系
等对等定理
O
A
B
C
D
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
(1)∵ ∠AOB=∠COD
几何语言:
O
A
B
C
D
∴ AB=CD , AB=CD
⌒
⌒
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
(2)∵ AB=CD
∴ AB=CD ,∠AOB=∠COD
⌒
⌒
(3)∵ AB=CD
⌒
⌒
∴ AB=CD ,∠AOB=∠COD
等对等定理
如图,在⊙O中,
例:如图,AB、DE是⊙O的直径,C是⊙O上的一点,且AD=CE。BE与CE的大小有什么关系?为什么?
⌒
⌒
B
E
O
D
A
C
BE=CE;理由是:
∵ ∠AOD=∠BOE
∴ AD=BE
⌒
⌒
又∵ AD=CE
⌒
⌒
∴ BE=CE
⌒
⌒
∴ BE=CE
答:
练习1:如图,A、B、C、D是⊙O上的四点, AB=DC ,△ABC与△DCB全等吗?为什么?
·
O
A
B
C
D
答:
全等;理由是:
∵ AB=DC
∴ AC=DB
又∵AB=DC,BC=CB
∴ AB=DC
⌒
⌒
⌒
∴ AB+BC=DC+BC
⌒
⌒
⌒
∴ AC=DB
⌒
⌒
∴ △ABC≌△DCB(SSS)
+
·
O
D
C
A
B
F
E
练习2:如图,在⊙O中, AB,CD是两条弦 ,OE⊥AB,OF⊥CD,垂足分别为E,F。
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系?AB与CD的大小有什么关系? ∠AOB=∠COD呢?为什么?
⌒
⌒
解: (1)OE=OF;理由是:
在⊙O中,OA=OB=OC=OD
∵ OE⊥AB,OF⊥CD
∴ ∠AEO=∠CFO=90°,∠AOE=∠BOE= ∠AOB,
∠COF=∠DOF= ∠COD
∵ ∠AOB=∠COD
∴ ∠AOE= ∠COF
又∵ ∠AEO=∠CFO,OA=OC
∴△AOE≌△COF(AAS)
∴OE=OF
从圆心到弦的距离叫弦心距。
·
O
D
C
A
B
F
E
练习2:如图,在⊙O中, AB,CD是两条弦 ,OE⊥AB,OF⊥CD,垂足分别为E,F。
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系?AB与CD的大小有什么关系? ∠AOB=∠COD呢?为什么?
⌒
⌒
(2)∵ OE⊥AB,OF⊥CD
∴ ∠AEO=∠CFO=90°
∵ OE=OF,OA=OC
∴Rt△AOE≌Rt△COF(HL)
∴AE=CF
同理得,Rt△BOE≌Rt△DOF
∴BE=DF
∴AE+ BE =CF+DF
∴AB=CD
∴AB=CD,∠AOB=∠COD
⌒
⌒
≌
≌
≌
≌
推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
1、圆的特殊对称性。
2、在同圆或等圆中,圆心 角、弧、弦之间的关系。
小结:
·
