3.6.1直线和圆的位置关系ls
图片预览





文档简介
(共20张PPT)
3.6.1 直线与圆的位置关系
罗湖外语实验学校
雷珊珊
1.如图:平面内点与圆的位置关系有:____、___、_____.
.A
. B
.C
(1)C点在圆内
(2)B点在圆上
(3)A点在圆外
2. 设⊙O的半径为r,点到圆心O的距离为d,那么:
O
r
d__r
d__r
d__r
>
=
<
圆外
圆上
圆内
一、知识回顾
(1)如果把太阳看作圆,地平线看作直线,你能用图形表示出上面地平线与圆之间的位置关系吗?
同学们在海边看过日出吗?请你用数学的眼光来欣赏 这幅“海上日出”图(多媒体出示) .
二、创设情境 引入新课
●O
a(地平线)
●O
●O
●O
●O
(2)观察下图中地平线与太阳的位置关系,说说直线与圆的公共点个数如何变化?由此你能得出直线和圆的位置关系分为几种情况?
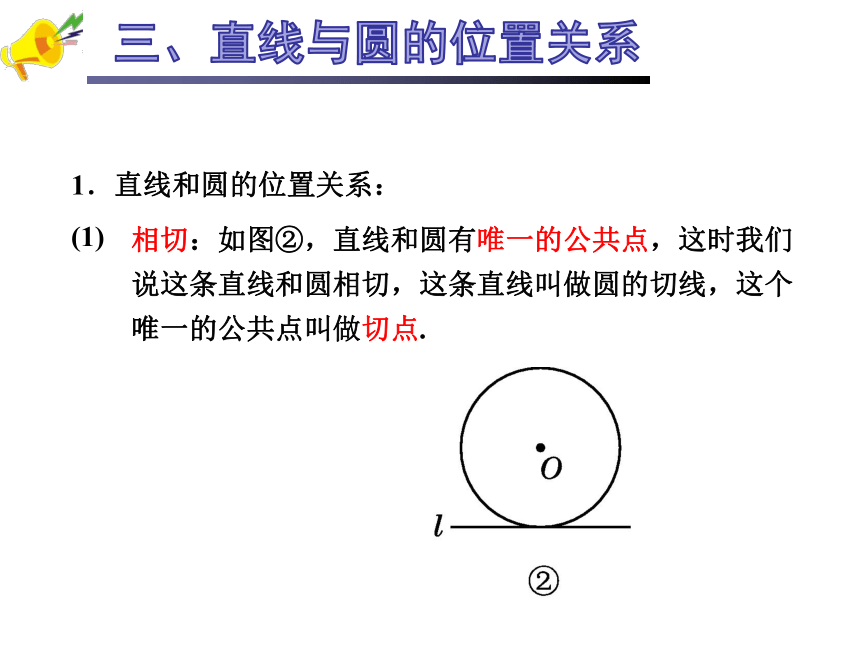
1.直线和圆的位置关系:
(1)
相切:如图②,直线和圆有唯一的公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
三、直线与圆的位置关系
(3)相离:如图③,直线和圆没有公共点,这时我们说这条直
线和圆相离.
知1-讲
(2)相交: 如图①,直线和圆有两个公共点,这时我们
说这条直线和圆相交,公共点叫做交点,这条直线
叫做圆的割线.
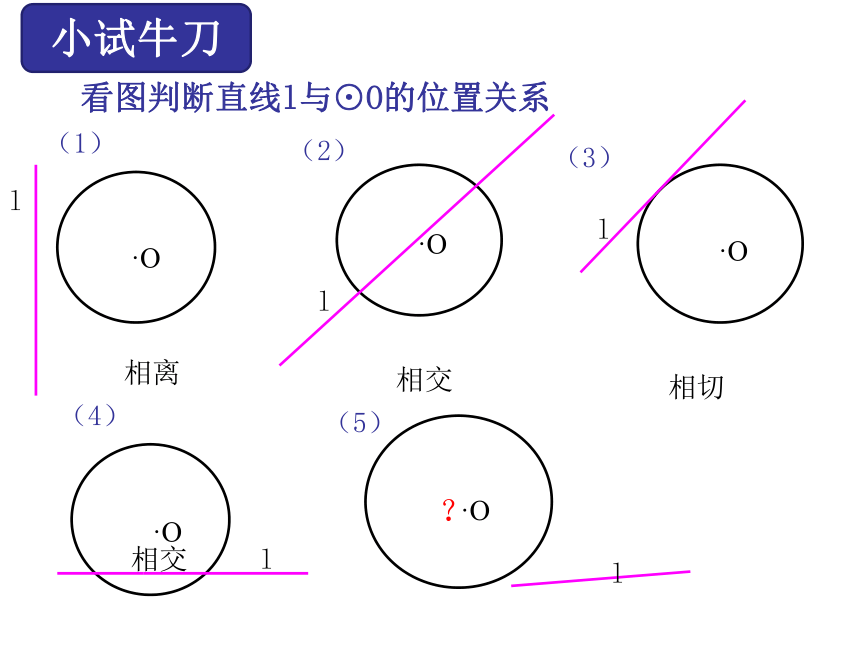
看图判断直线l与⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
小试牛刀
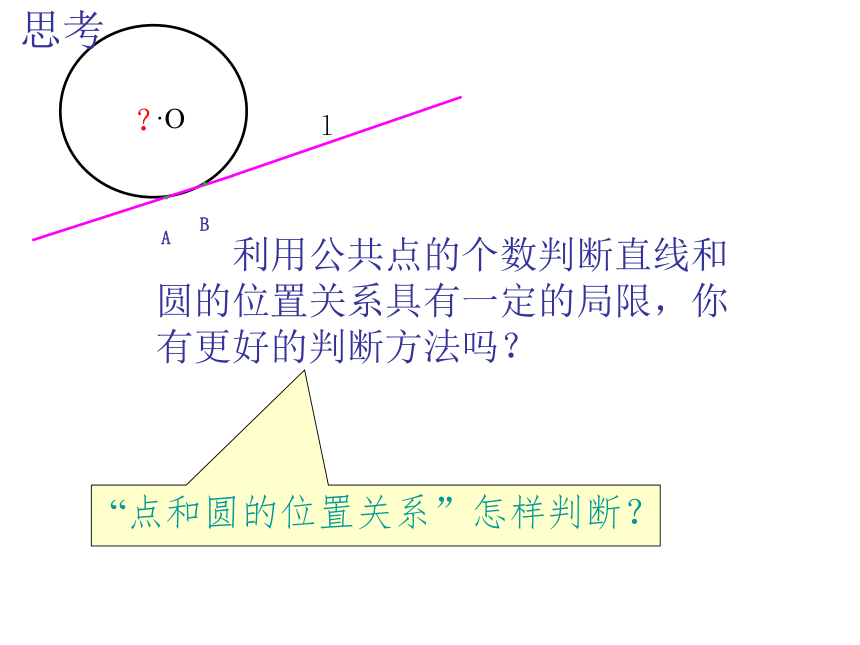
思考
?
l
利用公共点的个数判断直线和圆的位置关系具有一定的局限,你有更好的判断方法吗?
·O
·
A
·
B
“点和圆的位置关系”怎样判断?
.O
l
┐
d
r
.o
l
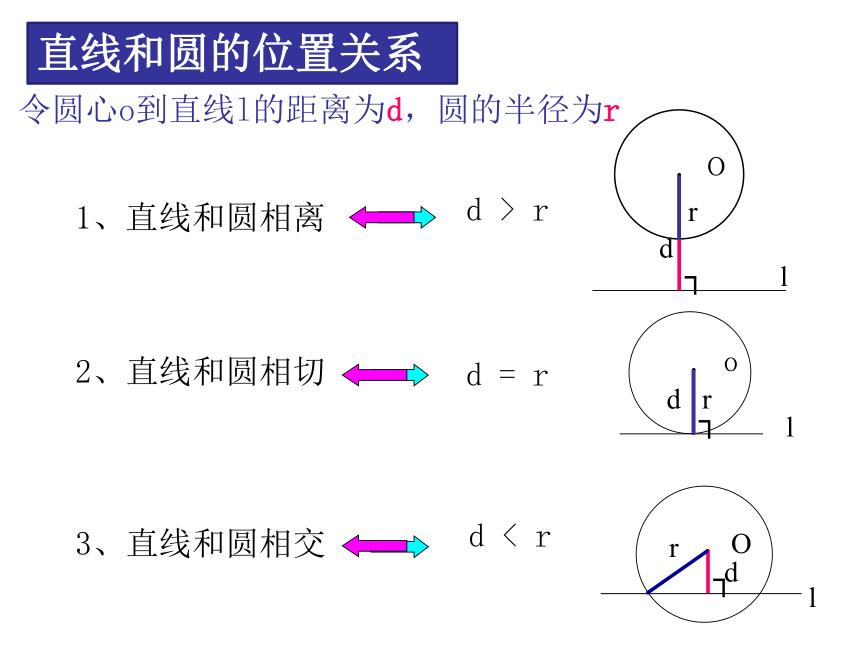
2、直线和圆相切
┐
d
r
d = r
.O
l
3、直线和圆相交
d < r
d
┐
r
1、直线和圆相离
d > r
直线和圆的位置关系
令圆心o到直线l的距离为d,圆的半径为r
1.已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .
2.直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .
d>5
r>8
3.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
C
小试牛刀
思考:求圆心A到X轴、
Y轴的距离各是多少
A.(-3,-4)
O
X
Y
4、已知⊙A的直径为6,点A的坐标为
(-3,-4),则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。
B
C
4
3
相离
相切
判断直线和圆的位置关系的方法有两种(如图): (1)根据定义中公共点的个数;
(2)根据d与r的数量关系.
温馨提示:
位置关系 基本图形 公共点个数 数量关系
相 交 2个 d相 切 1个 d=r
相 离 0个 d如图,直线CD与⊙O相切于点A,直径AB与直线CD有怎样的位置关系 说说你的理由.
答:直径AB垂直于直线CD.
理由:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.
C
D
B
●O
A
四、切线的性质
切线的性质定理:
定理 圆的切线垂直于过切点的半径.
老师提示:常用辅助线
根据切线的性质定理证明两线垂直时,常作过切点的半径.
符号语言:
∵CD是⊙O的切线,A是切点,
OA是⊙O的半径,
∴CD⊥OA.
C
D
B
●O
A
基本图形
切线的性质定理推论:
(1)经过圆心且垂直于切线的直线必过切点。
(2)经过切点且垂直于切线的直线必过圆心。
归纳: (1)垂直于切线
(2)过切点
(3)过圆心
圆中一条直线满足三个条件中任意2个,一定满则第三个
如图,在△ABC中,AB=1,AC= ,点O在AB的延长线上,AC切⊙O于点C.求:
(1)⊙O的半径;
(2)∠A的度数.
连接OC,易得Rt△OAC,运用勾股定理求⊙O的
半径.在Rt△OAC中,利用锐角三角函数求∠A
的度数.
导引:
小试牛刀
知2-讲
(1)连接OC.
∵AC切⊙O于点C,∴OC⊥AC,
设⊙O的半径为r,则OC=OB=r.
∴OA=OB+AB=1+r.
在Rt△OAC中,OA2=OC2+AC2,
即(1+r)2=r2+( )2,解得r=1.故⊙O的半径为1.
(2)由(1)得OC=1,OA=2.
在Rt△OAC中,sin A= ,∴∠A=30°.
解:
五、课堂小结
本节课你学到了什么?
六、作业布置
课本P91 习题3.7
六、作业布置
课本P87 习题3.6
3.6.1 直线与圆的位置关系
罗湖外语实验学校
雷珊珊
1.如图:平面内点与圆的位置关系有:____、___、_____.
.A
. B
.C
(1)C点在圆内
(2)B点在圆上
(3)A点在圆外
2. 设⊙O的半径为r,点到圆心O的距离为d,那么:
O
r
d__r
d__r
d__r
>
=
<
圆外
圆上
圆内
一、知识回顾
(1)如果把太阳看作圆,地平线看作直线,你能用图形表示出上面地平线与圆之间的位置关系吗?
同学们在海边看过日出吗?请你用数学的眼光来欣赏 这幅“海上日出”图(多媒体出示) .
二、创设情境 引入新课
●O
a(地平线)
●O
●O
●O
●O
(2)观察下图中地平线与太阳的位置关系,说说直线与圆的公共点个数如何变化?由此你能得出直线和圆的位置关系分为几种情况?
1.直线和圆的位置关系:
(1)
相切:如图②,直线和圆有唯一的公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
三、直线与圆的位置关系
(3)相离:如图③,直线和圆没有公共点,这时我们说这条直
线和圆相离.
知1-讲
(2)相交: 如图①,直线和圆有两个公共点,这时我们
说这条直线和圆相交,公共点叫做交点,这条直线
叫做圆的割线.
看图判断直线l与⊙O的位置关系
(1)
(2)
(3)
(4)
(5)
相离
相切
相交
相交
?
l
l
l
l
l
·O
·O
·O
·O
·O
小试牛刀
思考
?
l
利用公共点的个数判断直线和圆的位置关系具有一定的局限,你有更好的判断方法吗?
·O
·
A
·
B
“点和圆的位置关系”怎样判断?
.O
l
┐
d
r
.o
l
2、直线和圆相切
┐
d
r
d = r
.O
l
3、直线和圆相交
d < r
d
┐
r
1、直线和圆相离
d > r
直线和圆的位置关系
令圆心o到直线l的距离为d,圆的半径为r
1.已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .
2.直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .
d>5
r>8
3.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
C
小试牛刀
思考:求圆心A到X轴、
Y轴的距离各是多少
A.(-3,-4)
O
X
Y
4、已知⊙A的直径为6,点A的坐标为
(-3,-4),则X轴与⊙A的位置关系是_____, Y轴与⊙A的位置关系是______。
B
C
4
3
相离
相切
判断直线和圆的位置关系的方法有两种(如图): (1)根据定义中公共点的个数;
(2)根据d与r的数量关系.
温馨提示:
位置关系 基本图形 公共点个数 数量关系
相 交 2个 d
相 离 0个 d
答:直径AB垂直于直线CD.
理由:
∵右图是轴对称图形,AB是对称轴,
∴沿直线AB对折图形时,AC与AD重合,因此,∠BAC=∠BAD=90°.
C
D
B
●O
A
四、切线的性质
切线的性质定理:
定理 圆的切线垂直于过切点的半径.
老师提示:常用辅助线
根据切线的性质定理证明两线垂直时,常作过切点的半径.
符号语言:
∵CD是⊙O的切线,A是切点,
OA是⊙O的半径,
∴CD⊥OA.
C
D
B
●O
A
基本图形
切线的性质定理推论:
(1)经过圆心且垂直于切线的直线必过切点。
(2)经过切点且垂直于切线的直线必过圆心。
归纳: (1)垂直于切线
(2)过切点
(3)过圆心
圆中一条直线满足三个条件中任意2个,一定满则第三个
如图,在△ABC中,AB=1,AC= ,点O在AB的延长线上,AC切⊙O于点C.求:
(1)⊙O的半径;
(2)∠A的度数.
连接OC,易得Rt△OAC,运用勾股定理求⊙O的
半径.在Rt△OAC中,利用锐角三角函数求∠A
的度数.
导引:
小试牛刀
知2-讲
(1)连接OC.
∵AC切⊙O于点C,∴OC⊥AC,
设⊙O的半径为r,则OC=OB=r.
∴OA=OB+AB=1+r.
在Rt△OAC中,OA2=OC2+AC2,
即(1+r)2=r2+( )2,解得r=1.故⊙O的半径为1.
(2)由(1)得OC=1,OA=2.
在Rt△OAC中,sin A= ,∴∠A=30°.
解:
五、课堂小结
本节课你学到了什么?
六、作业布置
课本P91 习题3.7
六、作业布置
课本P87 习题3.6
