3.5确定圆的条件课件ls
图片预览


文档简介
(共18张PPT)
3.5 确定圆的条件
罗湖外语实验学校
雷珊珊
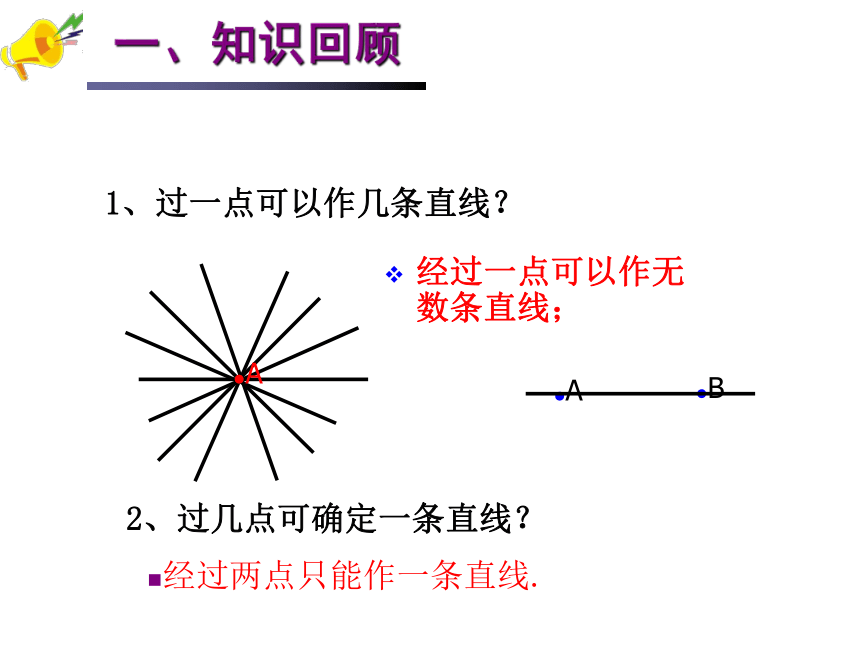
1、过一点可以作几条直线?
经过一点可以作无数条直线;
●A
2、过几点可确定一条直线?
经过两点只能作一条直线.
●A
●B
一、知识回顾
过几点可以确定一个圆呢?
思考:构成圆的基本要素有那些
两个条件:
圆心
半径
二、确定圆的条件
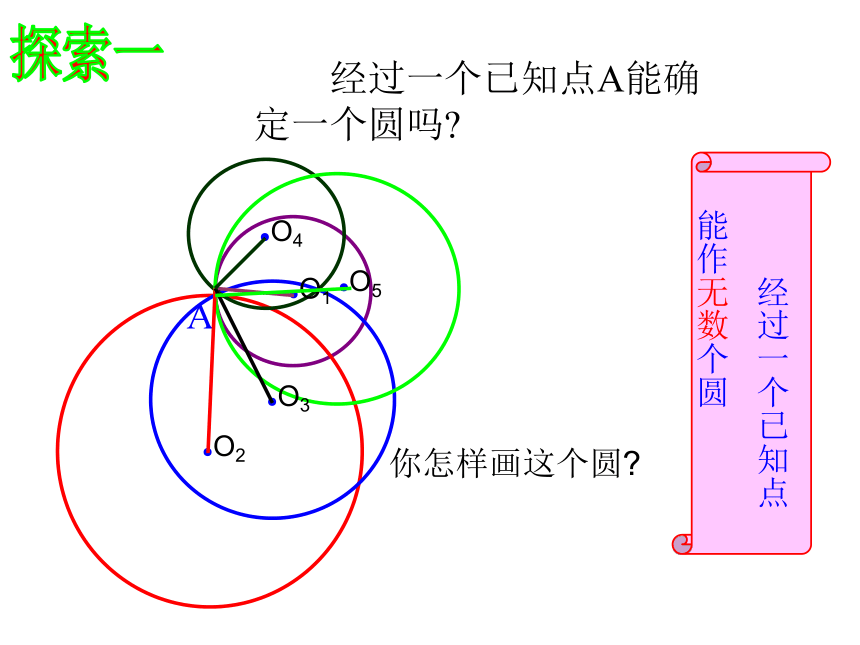
探索一
经过一个已知点A能确定一个圆吗
A
经过一个已知点
能作无数个圆
你怎样画这个圆
●O1
●O2
●O3
●O5
●O4
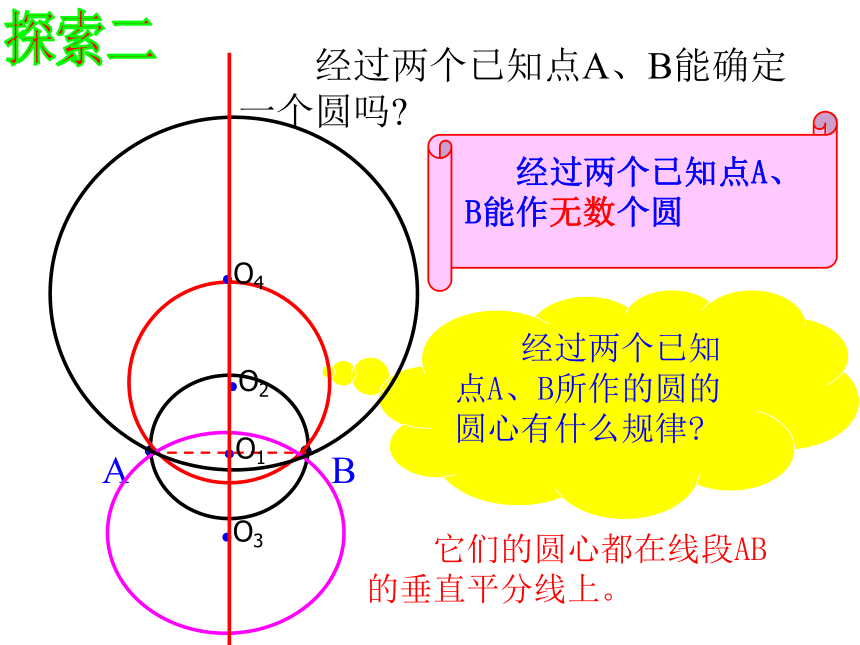
探索二
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心有什么规律
它们的圆心都在线段AB的垂直平分线上。
●O1
●O2
●O3
●O4
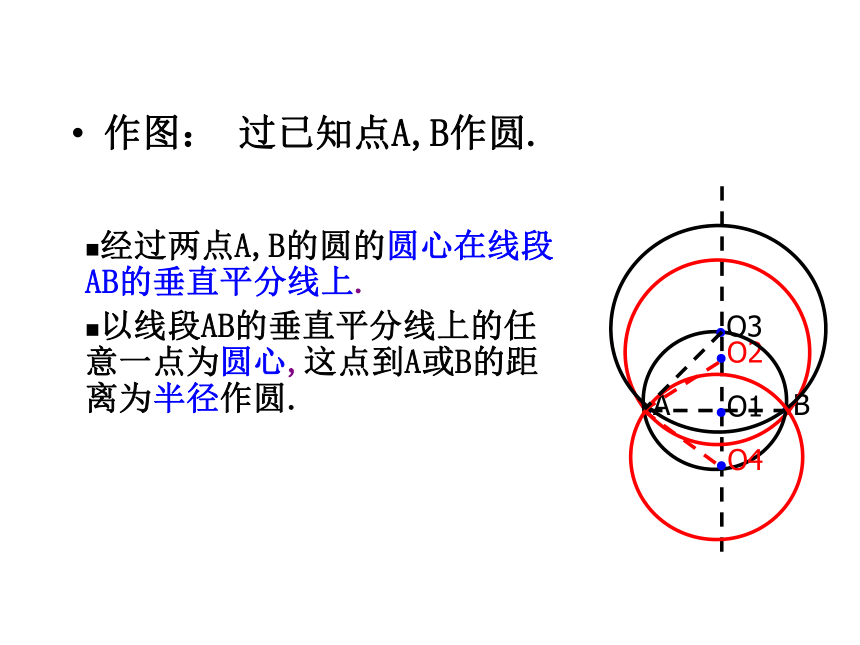
作图: 过已知点A,B作圆.
经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
●A
●B
●O2
●O1
●O3
●O4
探索三
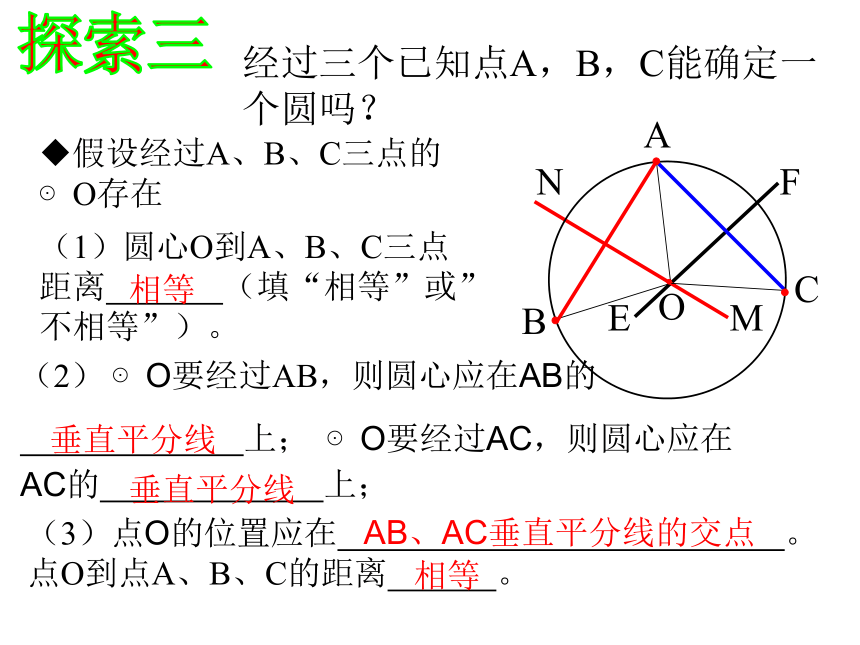
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2) ⊙O要经过AB,则圆心应在AB的
上; ⊙O要经过AC,则圆心应在AC的 上;
(3)点O的位置应在 。点O到点A、B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
AB、AC垂直平分线的交点
A
B
C
过如下三点能不能做圆 为什么
讨论
画一画
已知:不在同一直线上的三点A、B、C
求作: ⊙O使它经过点A、B、C
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
定理:
不在同一直线上的三点确定一个圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,
它到三角形的三个顶点的距离相等。
C
A
B
O
三、三个概念
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
(图一)
(图二)
(图三)
自主探究
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
如何将一个如图所示的破损的圆盘复原?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
1、如图,请找出图中圆的圆心,并写出你找圆心的方法
A
B
C
O
四、当堂检测
2.下列命题不正确的是
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
3.三角形的外心具有的性质是
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
4.等腰三角形底边上的高与一腰的垂直平分线的交点是
A.重心 B.垂心 C.外心 D.无法确定.
C
B
C
5.思考:任意四个点是不是可以作一个圆?请举例说明.
不一定
1. 四点在一条直线上不能作圆;
3. 四点中任意三点不在一条直线可能作圆也可能作不出一个圆.
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
2. 三点在同一直线上, 另一点不在这条直线上不能作圆;
本节课你学到了什么?
五、课堂小结
六、作业布置
课本P87 习题3.6
3.5 确定圆的条件
罗湖外语实验学校
雷珊珊
1、过一点可以作几条直线?
经过一点可以作无数条直线;
●A
2、过几点可确定一条直线?
经过两点只能作一条直线.
●A
●B
一、知识回顾
过几点可以确定一个圆呢?
思考:构成圆的基本要素有那些
两个条件:
圆心
半径
二、确定圆的条件
探索一
经过一个已知点A能确定一个圆吗
A
经过一个已知点
能作无数个圆
你怎样画这个圆
●O1
●O2
●O3
●O5
●O4
探索二
经过两个已知点A、B能确定一个圆吗
A
B
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心有什么规律
它们的圆心都在线段AB的垂直平分线上。
●O1
●O2
●O3
●O4
作图: 过已知点A,B作圆.
经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
●A
●B
●O2
●O1
●O3
●O4
探索三
经过三个已知点A,B,C能确定一个圆吗?
假设经过A、B、C三点的⊙O存在
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”)。
(2) ⊙O要经过AB,则圆心应在AB的
上; ⊙O要经过AC,则圆心应在AC的 上;
(3)点O的位置应在 。点O到点A、B、C的距离 。
N
M
F
E
O
A
B
C
相等
垂直平分线
垂直平分线
相等
AB、AC垂直平分线的交点
A
B
C
过如下三点能不能做圆 为什么
讨论
画一画
已知:不在同一直线上的三点A、B、C
求作: ⊙O使它经过点A、B、C
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆。
O
N
M
F
E
A
B
C
定理:
不在同一直线上的三点确定一个圆
经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形。
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,
它到三角形的三个顶点的距离相等。
C
A
B
O
三、三个概念
画出过以下三角形的顶点的圆
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
(图一)
(图二)
(图三)
自主探究
锐角三角形的外心位于三角形内.
直角三角形的外心位于直角三角形斜边中点.
钝角三角形的外心位于三角形外.
如何将一个如图所示的破损的圆盘复原?
方法:
1、在圆弧上任取三点A、B、C。
2、作线段AB、BC的垂直平分线,其交点O即为圆心。
3、以点O为圆心,OC长为半径作圆。
⊙O即为所求。
A
B
C
O
1、如图,请找出图中圆的圆心,并写出你找圆心的方法
A
B
C
O
四、当堂检测
2.下列命题不正确的是
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
3.三角形的外心具有的性质是
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
4.等腰三角形底边上的高与一腰的垂直平分线的交点是
A.重心 B.垂心 C.外心 D.无法确定.
C
B
C
5.思考:任意四个点是不是可以作一个圆?请举例说明.
不一定
1. 四点在一条直线上不能作圆;
3. 四点中任意三点不在一条直线可能作圆也可能作不出一个圆.
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
2. 三点在同一直线上, 另一点不在这条直线上不能作圆;
本节课你学到了什么?
五、课堂小结
六、作业布置
课本P87 习题3.6
