第三章圆3.3垂径定理课件
图片预览


文档简介
(共15张PPT)
3.3垂径定理
2.它的对称轴是什么
是
圆的对称轴是任意一条经过圆心的直线
3.你能找到多少条对称轴?
它有无数条对称轴.
●O
1.圆是轴对称图形吗?
知识回顾
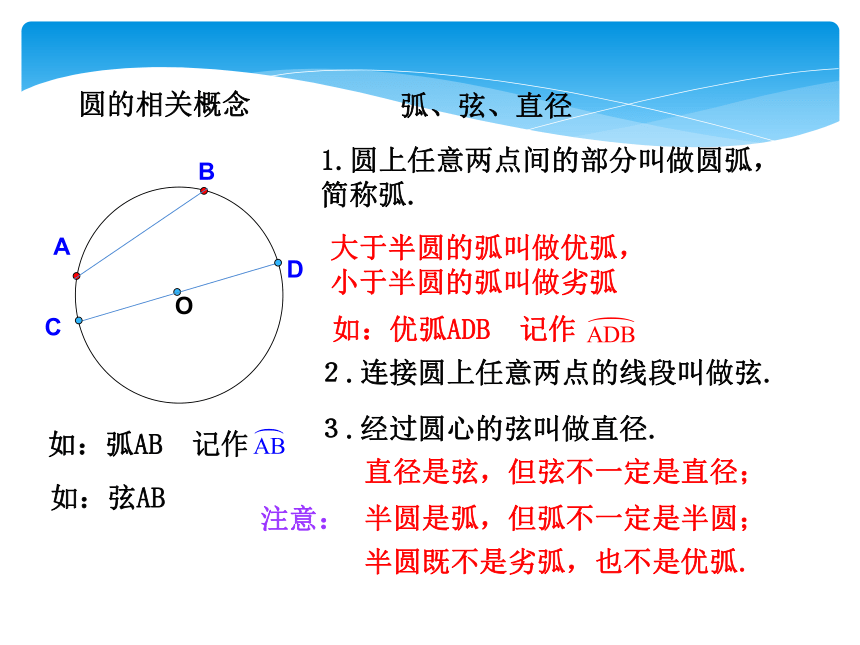
1.圆上任意两点间的部分叫做圆弧,简称弧.
大于半圆的弧叫做优弧,
小于半圆的弧叫做劣弧
2.连接圆上任意两点的线段叫做弦.
如:弦AB
3.经过圆心的弦叫做直径.
直径是弦,但弦不一定是直径;
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧.
弧、弦、直径
注意:
A
B
O
D
C
圆的相关概念
如:优弧ADB 记作
如:弧AB 记作
③AM=BM,
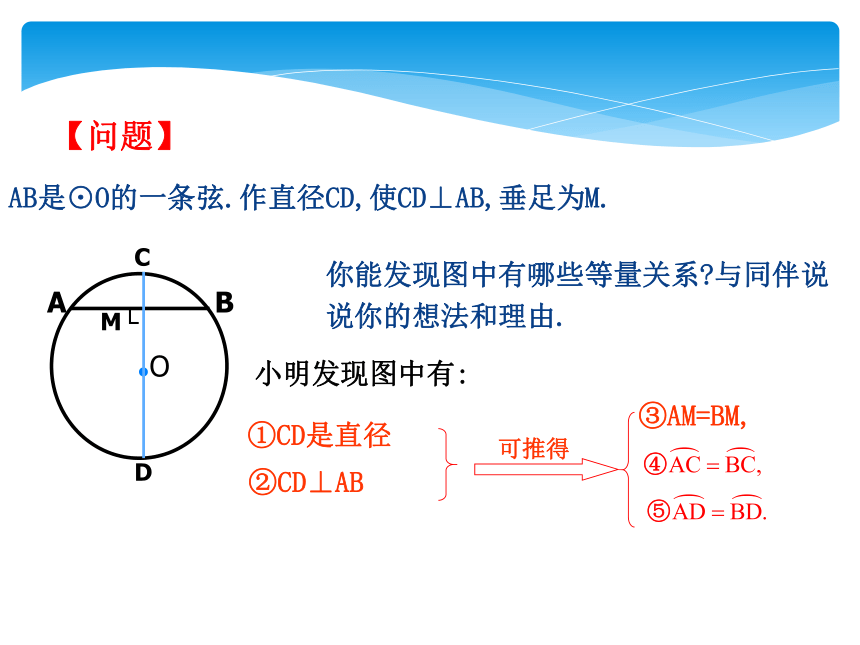
AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
●O
小明发现图中有:
A
B
C
D
M└
①CD是直径
②CD⊥AB
可推得
【问题】
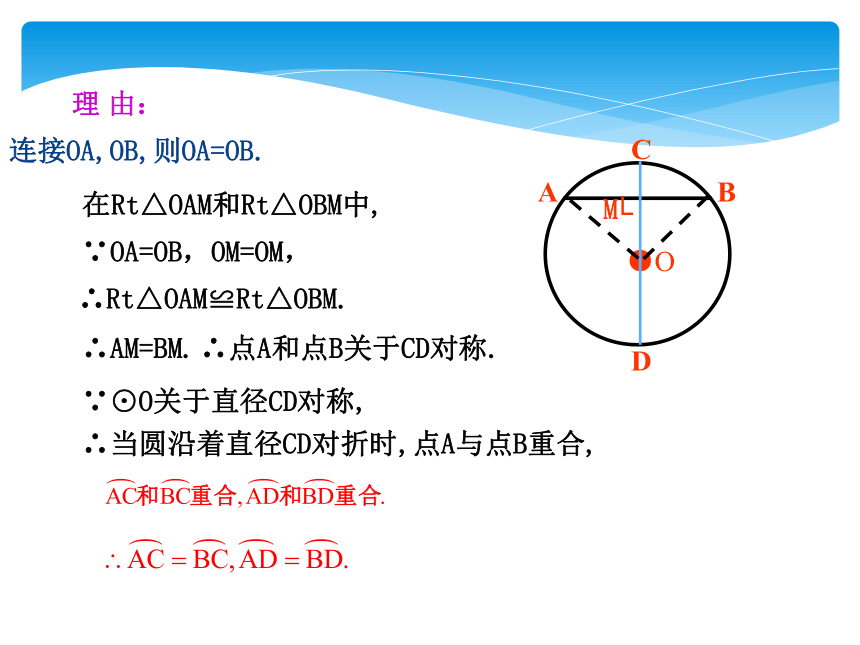
连接OA,OB,则OA=OB.
●O
A
B
C
D
└
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
理 由:
M
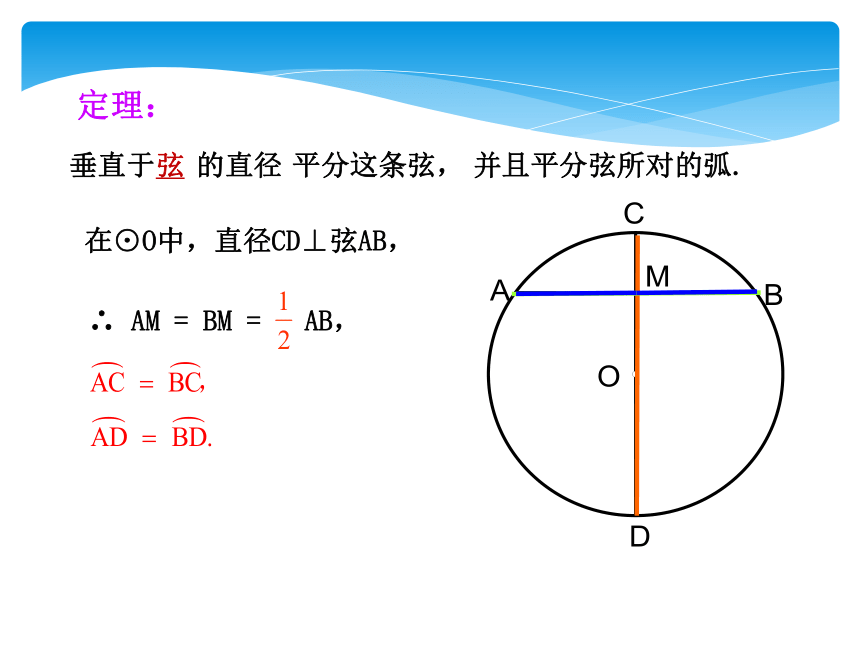
垂直于
平分这条弦,
并且平分弦所对的弧.
弦
的直径
在⊙O中,直径CD⊥弦AB,
∴ AM = BM = AB,
定理:
┗
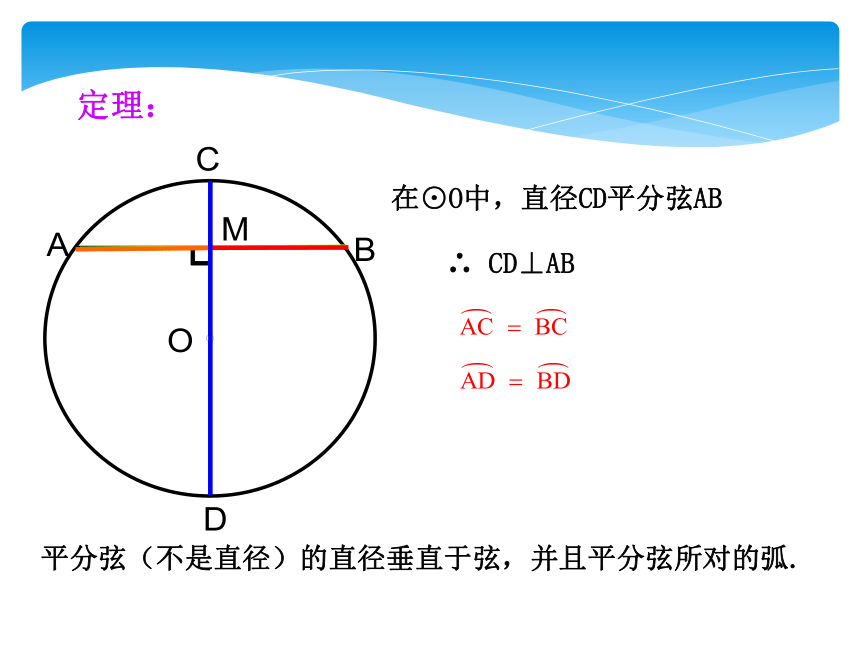
在⊙O中,直径CD平分弦AB
∴ CD⊥AB
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
定理:
弦
(不是直径)
并且平分弦所对的弧
平分
的直径
垂直于弦,
结论:
例.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB.
└
【例题】
解:连接OA,
在⊙O中,直径CD⊥AB,
∴ AB =2AM,
△OMA是直角三角形.
∵ CD = 20,
∴ AO = CO = 10.
∴ OM = OC – CM = 10 – 4 = 6.
在Rt △OMA中,AO = 10,OM = 6,
根据勾股定理,得:
∴
∴ AB = 2AM = 2 × 8 = 16.
└
例.如图,一条公路的转弯处是一段圆弧(即图中 ,点
O是 所在圆的圆心),其中CD=600m,E是 上一点,且
OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
└
解:连接OC.
已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm B.7 cm
C.12 cm D.17 cm或7 cm
图(1) 图(2)
答案:D
练习
【规律方法】运用垂径定理及其推论解决一些数学问题.最常见的辅助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂线,构造直角三角形,利用勾股定理解决问题.
1.圆的相关概念,弦、弧、优弧、劣弧.
2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
通过本课时的学习,需要我们掌握:
善良和谦虚是永远不应令人厌恶的两种品德。
——斯蒂文生
3.3垂径定理
2.它的对称轴是什么
是
圆的对称轴是任意一条经过圆心的直线
3.你能找到多少条对称轴?
它有无数条对称轴.
●O
1.圆是轴对称图形吗?
知识回顾
1.圆上任意两点间的部分叫做圆弧,简称弧.
大于半圆的弧叫做优弧,
小于半圆的弧叫做劣弧
2.连接圆上任意两点的线段叫做弦.
如:弦AB
3.经过圆心的弦叫做直径.
直径是弦,但弦不一定是直径;
半圆是弧,但弧不一定是半圆;
半圆既不是劣弧,也不是优弧.
弧、弦、直径
注意:
A
B
O
D
C
圆的相关概念
如:优弧ADB 记作
如:弧AB 记作
③AM=BM,
AB是⊙O的一条弦.作直径CD,使CD⊥AB,垂足为M.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
●O
小明发现图中有:
A
B
C
D
M└
①CD是直径
②CD⊥AB
可推得
【问题】
连接OA,OB,则OA=OB.
●O
A
B
C
D
└
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
理 由:
M
垂直于
平分这条弦,
并且平分弦所对的弧.
弦
的直径
在⊙O中,直径CD⊥弦AB,
∴ AM = BM = AB,
定理:
┗
在⊙O中,直径CD平分弦AB
∴ CD⊥AB
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
定理:
弦
(不是直径)
并且平分弦所对的弧
平分
的直径
垂直于弦,
结论:
例.如图,在⊙O中,CD是直径,AB是弦,且CD⊥AB,已知CD = 20,CM = 4,求AB.
└
【例题】
解:连接OA,
在⊙O中,直径CD⊥AB,
∴ AB =2AM,
△OMA是直角三角形.
∵ CD = 20,
∴ AO = CO = 10.
∴ OM = OC – CM = 10 – 4 = 6.
在Rt △OMA中,AO = 10,OM = 6,
根据勾股定理,得:
∴
∴ AB = 2AM = 2 × 8 = 16.
└
例.如图,一条公路的转弯处是一段圆弧(即图中 ,点
O是 所在圆的圆心),其中CD=600m,E是 上一点,且
OE⊥CD,垂足为F,EF=90m,求这段弯路的半径.
└
解:连接OC.
已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,则AB,CD之间的距离为( )
A.17cm B.7 cm
C.12 cm D.17 cm或7 cm
图(1) 图(2)
答案:D
练习
【规律方法】运用垂径定理及其推论解决一些数学问题.最常见的辅助线是连接圆上的点与圆心构成半径,及过圆心作弦的垂线,构造直角三角形,利用勾股定理解决问题.
1.圆的相关概念,弦、弧、优弧、劣弧.
2.垂径定理及推论、圆的对称性.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
通过本课时的学习,需要我们掌握:
善良和谦虚是永远不应令人厌恶的两种品德。
——斯蒂文生
