3.4 圆周角和圆心角的关系第1课时 教案
文档属性
| 名称 | 3.4 圆周角和圆心角的关系第1课时 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 14.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 00:00:00 | ||
图片预览



文档简介
第三章 圆
3.4 圆周角和圆心角的关系第一课时
一、学情分析
学生的知识技能基础:学生在上一节的内容中已掌握了圆心角的定义及圆心角的性质。掌握了在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。初步了解研究图形的方法,如折叠、轴对称、旋转、证明等。
学生的活动经验基础:在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
2、教材分析
《圆周角与圆心角之间的关系》是北师大版九年级下册第三章第3小节的内容,是学生学习了圆心、半径、直径、弦、弧,圆心角等概念以及圆的对称性的基础上,用推理论证的方法研究圆周角与圆心角之间的关系。它在与圆有关推理、论证和计算中应用广泛,是本章重点内容之一。
三、教学任务分析
本节共分2个课时,这是第1课时,主要研究圆周角和圆心角的关系(圆周角定理),具体地说,本节课的教学目标为:
知识与技能
1.了解圆周角的概念。
2.理解圆周角定理的证明。
过程与方法
1.经历探索圆周角和圆心角的关系的过程,学会以特殊情况为基础,通过转化来解决一般性问题的方法,渗透分类的数学思想。
2.体会由特殊到一般、分类、化归思想,并能熟练的应用“圆周角与圆心角之间的关系”进行论证和计算。
情感态度与价值观
通过观察、猜想、验证推理,培养学生探索问题的能力和方法。
教学重点:圆周角概念及圆周角定理。
教学难点:认识圆周角定理需分三种情况证明的必要性,感悟圆周角定理证明中的分类、转化的数学思想。
三、教学过程分析
本节课分为五个教学环节:创设问题情境引入新课、新知学习(关于圆周角的定义、圆周角定理)、练习、课堂小结、布置作业.
第一环节 (1)复习引入
1.圆心角的定义
答:顶点在圆心的角叫圆心角.
2.圆心角和它所对的弧的关系
答:在同圆或等圆中,相等的圆心角所对的弧也相等。
(2)创设问题情境,引入新课
通过一个视频,国足在2017年俄罗斯世预赛12强赛第6轮的比赛中战胜韩国,引出足球射门这一情景:
情境:在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。如图,当他站在B,D,E的位置射球时对球门AC的张角的大小相等吗?为你能观察到这三个角有什么共同特征吗
第二环节 新知学习
合作探究一 圆周角的定义
(一)圆周角的定义的学习
你观察到这几个角有什么共同特征呢?
可以发现,它的顶点在圆上,它的两边分别与圆还有另一个交点。像这样的角,叫做圆周角。
你能仿照圆心角的概念给圆周角下一个定义吗?
圆周角定义: 顶点在圆上,并且两边分别与圆 还有另一个交点的角叫圆周角.
追踪练习:
(1)顶点在圆上的角是圆周角吗?
(2)角的两边都和圆相交的角是圆周角吗?
判断下列图示中,各图形中的角是不是圆周角?并说明理由。
通过学生完成练习自己总结出圆周角的特征。
圆周角有两个特征:
①角的顶点在圆上;
两边在圆内的部分是圆的两条弦。
(二)圆周角定理的学习
我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
归纳同学们的意见我们得到以下几种情况:
合作探究2 圆周角的性质
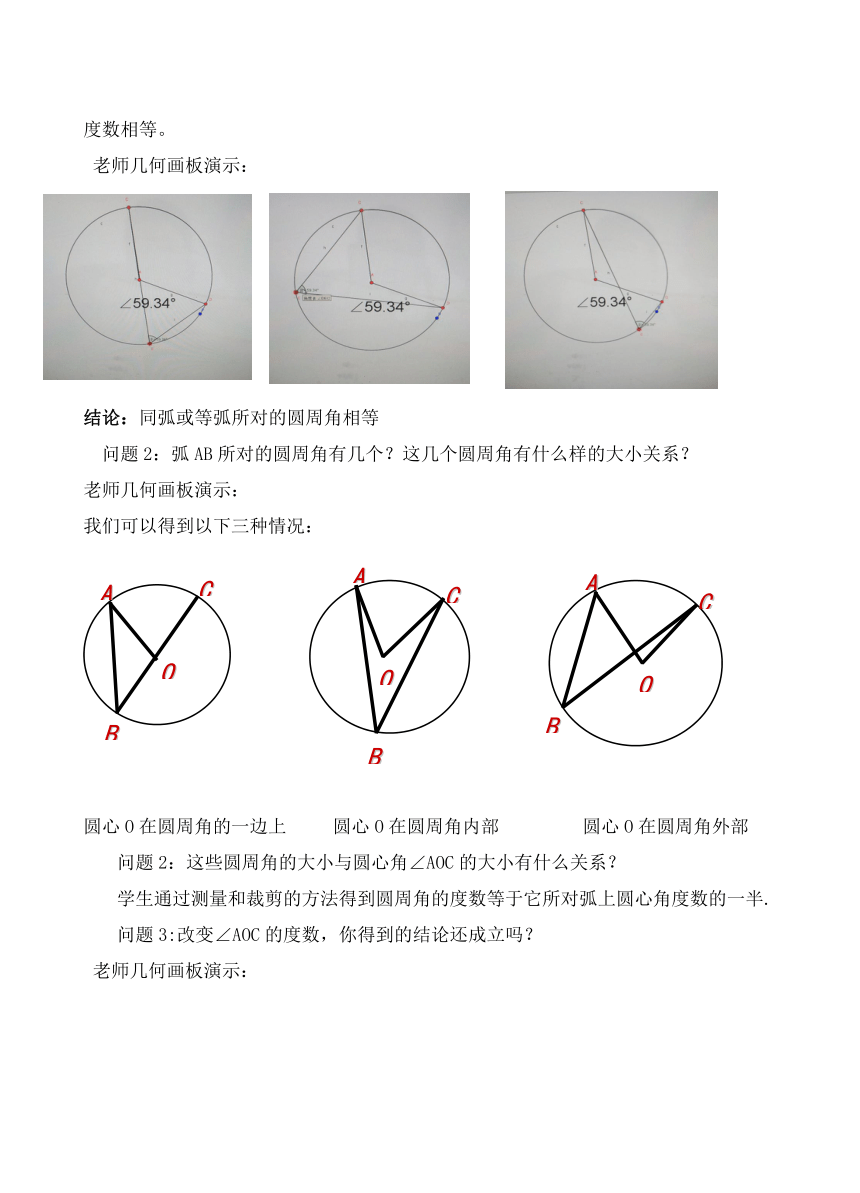
问题1:弧AB所对的圆周角有几个?这几个圆周角有什么样的大小关系?
学生先通过测量和剪拼的方法得到同一条弧所对的圆周角有无数个,这些圆周角的度数相等。
老师几何画板演示:
结论:同弧或等弧所对的圆周角相等
问题2:弧AB所对的圆周角有几个?这几个圆周角有什么样的大小关系?
老师几何画板演示:
我们可以得到以下三种情况:
圆心O在圆周角的一边上 圆心O在圆周角内部 圆心O在圆周角外部
问题2:这些圆周角的大小与圆心角∠AOC的大小有什么关系?
学生通过测量和裁剪的方法得到圆周角的度数等于它所对弧上圆心角度数的一半.
问题3:改变∠AOC的度数,你得到的结论还成立吗?
老师几何画板演示:
结论:(1)圆周角的度数等于它所对弧上圆心角度数的一半.
(2)同弧或等弧所对的圆周角相等
下面大家一起来证明我们等到的第一个结论是否正确
情况一:当圆心(O)在∠B的一边上时, ∠B与∠AOC的大小关系?
学生合作交流并在白板上由学生讲解板书证明过程.
结论:当圆心在圆周角一边上时,圆周角的度数等于它所对弧上圆心角度数的一半。
情况二:当圆心O在圆周角∠B的内部时,∠B与∠AOC的大小关系
提示:能否转化为1的情况
学生合作交流并在白板上由学生讲解板书证明过程.
结论:当圆心在圆周角内部时,圆周角的度数等于它所对弧上圆心角度数的一半.
情况三:当圆心结论:圆周角的度数等于它所对弧上圆心角度数的一半.
O在∠B的外部时,∠B与∠AOC的大小关系
学生合作交流并在白板上由学生讲解板书证明过程.
结论:当圆心在圆周角外部时,圆周角的度数等于它所对弧上圆心角度数的一半.
圆周角定理:
圆周角的度数等于它所对弧上圆心角度数的一半.
能否应用圆周角定理证明我们得到的第二个结论呢?
学生通过同弧或等弧所对的圆心角相等以及圆周角定理得到结论2是一个真命题.
推论:同弧或等弧所对的圆周角相等.
第三环节 当堂检测:
1.如图,∠BAC=40°,则∠BOC= ________ 。
2.如图,点B、C在⊙O上,且BO=BC,则圆周角∠BAC等于_____.
3.如图,A、B、C、D是⊙O上的四点,且∠BCD=100 °,则∠BOD=_____, ∠BAD____.
4.如图,在⊙O中,弦AB、CD相交于点E,∠ACD=40°, ∠CEB=75°,则∠CDB=______.
5.如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC.∠1= ∠2有什么大小关系?请说明理由?
第4题 第5题
第四环节 课堂小结:
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
3.圆周角定理推论:同弧(或等弧)所对的圆周角相等
第五环节 作业布置
必做题:教材80页第1题,第2题.
选做题:教材80页第3题
四、教学反思
把射门游戏问题抽象为数学问题,研究圆周角和圆心角的关系,研究圆周角和圆心角的关系,应该说,学生解决这一问题是有一定难度的,尽管如此,教学时仍应给学生留有时间和空间,让他们进行思考。让学生经历观察、想象、推理、操作、描述、交流等过程,多种角度直观体验数学模型,而这也正符合本章学习的主要目标。
A
C
B
A
O
C
A
B
C
O
B
A
C
O
3.4 圆周角和圆心角的关系第一课时
一、学情分析
学生的知识技能基础:学生在上一节的内容中已掌握了圆心角的定义及圆心角的性质。掌握了在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。初步了解研究图形的方法,如折叠、轴对称、旋转、证明等。
学生的活动经验基础:在以前的数学学习中学生已经经历了很多合作学习的过程,具有了一定的合作学习的经验,具备了一定的合作与交流的能力。
2、教材分析
《圆周角与圆心角之间的关系》是北师大版九年级下册第三章第3小节的内容,是学生学习了圆心、半径、直径、弦、弧,圆心角等概念以及圆的对称性的基础上,用推理论证的方法研究圆周角与圆心角之间的关系。它在与圆有关推理、论证和计算中应用广泛,是本章重点内容之一。
三、教学任务分析
本节共分2个课时,这是第1课时,主要研究圆周角和圆心角的关系(圆周角定理),具体地说,本节课的教学目标为:
知识与技能
1.了解圆周角的概念。
2.理解圆周角定理的证明。
过程与方法
1.经历探索圆周角和圆心角的关系的过程,学会以特殊情况为基础,通过转化来解决一般性问题的方法,渗透分类的数学思想。
2.体会由特殊到一般、分类、化归思想,并能熟练的应用“圆周角与圆心角之间的关系”进行论证和计算。
情感态度与价值观
通过观察、猜想、验证推理,培养学生探索问题的能力和方法。
教学重点:圆周角概念及圆周角定理。
教学难点:认识圆周角定理需分三种情况证明的必要性,感悟圆周角定理证明中的分类、转化的数学思想。
三、教学过程分析
本节课分为五个教学环节:创设问题情境引入新课、新知学习(关于圆周角的定义、圆周角定理)、练习、课堂小结、布置作业.
第一环节 (1)复习引入
1.圆心角的定义
答:顶点在圆心的角叫圆心角.
2.圆心角和它所对的弧的关系
答:在同圆或等圆中,相等的圆心角所对的弧也相等。
(2)创设问题情境,引入新课
通过一个视频,国足在2017年俄罗斯世预赛12强赛第6轮的比赛中战胜韩国,引出足球射门这一情景:
情境:在射门游戏中,球员射中球门的难易与他所处的位置B对球门AC的张角(∠ABC)有关。如图,当他站在B,D,E的位置射球时对球门AC的张角的大小相等吗?为你能观察到这三个角有什么共同特征吗
第二环节 新知学习
合作探究一 圆周角的定义
(一)圆周角的定义的学习
你观察到这几个角有什么共同特征呢?
可以发现,它的顶点在圆上,它的两边分别与圆还有另一个交点。像这样的角,叫做圆周角。
你能仿照圆心角的概念给圆周角下一个定义吗?
圆周角定义: 顶点在圆上,并且两边分别与圆 还有另一个交点的角叫圆周角.
追踪练习:
(1)顶点在圆上的角是圆周角吗?
(2)角的两边都和圆相交的角是圆周角吗?
判断下列图示中,各图形中的角是不是圆周角?并说明理由。
通过学生完成练习自己总结出圆周角的特征。
圆周角有两个特征:
①角的顶点在圆上;
两边在圆内的部分是圆的两条弦。
(二)圆周角定理的学习
我们先研究一条弧所对的圆周角与它所对的圆心角之间的关系。
请同学们在圆上确定一条劣弧,画出它所对的圆心角与圆周角。
归纳同学们的意见我们得到以下几种情况:
合作探究2 圆周角的性质
问题1:弧AB所对的圆周角有几个?这几个圆周角有什么样的大小关系?
学生先通过测量和剪拼的方法得到同一条弧所对的圆周角有无数个,这些圆周角的度数相等。
老师几何画板演示:
结论:同弧或等弧所对的圆周角相等
问题2:弧AB所对的圆周角有几个?这几个圆周角有什么样的大小关系?
老师几何画板演示:
我们可以得到以下三种情况:
圆心O在圆周角的一边上 圆心O在圆周角内部 圆心O在圆周角外部
问题2:这些圆周角的大小与圆心角∠AOC的大小有什么关系?
学生通过测量和裁剪的方法得到圆周角的度数等于它所对弧上圆心角度数的一半.
问题3:改变∠AOC的度数,你得到的结论还成立吗?
老师几何画板演示:
结论:(1)圆周角的度数等于它所对弧上圆心角度数的一半.
(2)同弧或等弧所对的圆周角相等
下面大家一起来证明我们等到的第一个结论是否正确
情况一:当圆心(O)在∠B的一边上时, ∠B与∠AOC的大小关系?
学生合作交流并在白板上由学生讲解板书证明过程.
结论:当圆心在圆周角一边上时,圆周角的度数等于它所对弧上圆心角度数的一半。
情况二:当圆心O在圆周角∠B的内部时,∠B与∠AOC的大小关系
提示:能否转化为1的情况
学生合作交流并在白板上由学生讲解板书证明过程.
结论:当圆心在圆周角内部时,圆周角的度数等于它所对弧上圆心角度数的一半.
情况三:当圆心结论:圆周角的度数等于它所对弧上圆心角度数的一半.
O在∠B的外部时,∠B与∠AOC的大小关系
学生合作交流并在白板上由学生讲解板书证明过程.
结论:当圆心在圆周角外部时,圆周角的度数等于它所对弧上圆心角度数的一半.
圆周角定理:
圆周角的度数等于它所对弧上圆心角度数的一半.
能否应用圆周角定理证明我们得到的第二个结论呢?
学生通过同弧或等弧所对的圆心角相等以及圆周角定理得到结论2是一个真命题.
推论:同弧或等弧所对的圆周角相等.
第三环节 当堂检测:
1.如图,∠BAC=40°,则∠BOC= ________ 。
2.如图,点B、C在⊙O上,且BO=BC,则圆周角∠BAC等于_____.
3.如图,A、B、C、D是⊙O上的四点,且∠BCD=100 °,则∠BOD=_____, ∠BAD____.
4.如图,在⊙O中,弦AB、CD相交于点E,∠ACD=40°, ∠CEB=75°,则∠CDB=______.
5.如图,OA、OB、OC都是⊙O的半径,∠AOB=2 ∠BOC.∠1= ∠2有什么大小关系?请说明理由?
第4题 第5题
第四环节 课堂小结:
1.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
3.圆周角定理推论:同弧(或等弧)所对的圆周角相等
第五环节 作业布置
必做题:教材80页第1题,第2题.
选做题:教材80页第3题
四、教学反思
把射门游戏问题抽象为数学问题,研究圆周角和圆心角的关系,研究圆周角和圆心角的关系,应该说,学生解决这一问题是有一定难度的,尽管如此,教学时仍应给学生留有时间和空间,让他们进行思考。让学生经历观察、想象、推理、操作、描述、交流等过程,多种角度直观体验数学模型,而这也正符合本章学习的主要目标。
A
C
B
A
O
C
A
B
C
O
B
A
C
O
