20.2数据的波动程度同步练习(含解析)
文档属性
| 名称 | 20.2数据的波动程度同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 580.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 17:33:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
20.2数据的波动程度
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,
方差分别是,,,.在本次射击测试中,成绩最
稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.在统计中,样本的方差可以近似的反映总体的( )
A.最大值与最小值 B.平均状态
C.分布规律 D.波动大小
3.体育课上,某班两名同学分别进行10次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的( )
A.平均数 B.众数 C.中位数 D.方差
4.在2017年的初中数学竞赛中,我校有5位同学获奖,他们的成绩分别是88,86,91,88,92.则由这组数据得到的以下结论,错误的是( )
A.极差为6 B.平均数为89 C.众数为88 D.中位数为91
5.教练组对运动员正式比赛前的5次训练成绩进行分析,判断谁的成绩更加稳定,一般需要考察这5次成绩的 ( )
A.平均数或中位数 B.众数或频率 C.方差或极差 D.频数或众数
6.甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,据此分析,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )
统计量 甲 乙 丙 丁
平均数 9.2 9.1 9.3 9.1
方差 0.60 0.62 0.50 0.44
A.甲 B.乙 C.丙 D.丁
7.一组数据3、4、4、5,若添加一个数4得到一组新数据,则前后两组数据的统计量会变小的是( )
A.平均数 B.中位数 C.众数 D.方差
8.一次中学生田径运动会上,21名参加男子跳高项目的运动员成绩统计如下:
成绩(m) 1.50 1.55 1.60 1.65 1.70
人数 ■ 8 6 ■ 1
其中有两个数据被雨水淋湿模糊不清了,则在这组数据中能确定的统计量是()
A.平均数 B.中位数 C.众数 D.方差
9.初中生每天的睡眠时间应为9个小时.鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则下列说法正确的是( )
A.鹏鹏这一周睡眠时间的中位数是7小时
B.鹏鹏这一周睡眠时间的众数是7小时
C.鹏鹏这一周睡眠时间的极差是4小时
D.鹏鹏这一周睡眠时间的平均数是8小时
10.从甲、乙、丙、丁四人中选出一人参加射击比赛,经过初赛统计,他们的平均成绩都是9环,方差分别是,,,,结合以上数据,你认为派谁参加比赛更合适( )
A.甲 B.乙 C.丙 D.丁
11.甲、乙两位同学进行“汉字拼写”训练,他们5次训练成绩的平均数均为90分,方差分别为,,则下列对两位同学成绩的稳定性描述正确的是( )
A.甲更稳定 B.乙更稳定 C.一样稳定 D.无法确定
12.某奶茶小店某月每日营业额(单位:元)中随机抽取部分数据,根据方差公式,得则下列说法正确的是( )
A.样本的容量是4 B.该组数据的中位数是400
C.该组数据的众数是300 D.
二、填空题
13.学完方差的知识后,小明了解了他最要好的四个朋友的身高,分别是176cm,174cm,177cm,173cm,那么小明四个好朋友身高的方差是 .
14.从甲、乙、丙三人中选拔一人参加职业技能大赛,经过几轮初赛选拔,他们的平均成绩都是87.9分,方差分别是s甲2=3.83,s乙2=2.71,s丙2=1.52.若选取成绩稳定的一人参加比赛,你认为适合参加比赛的选手是 .
15.已知一组数据0,1,2,2,x,3的平均数是2,则这组数据的方差是 .
16.一个样本容量为50的样本最大值为127,最小值为60,组距为10,则可分成 组.
17.一组数据为0,1,2,3,4,则这组数据的方差是 .
三、解答题
18.从甲、乙两台包装机包装的质量为300g的袋装食品中各抽取10袋,测得其实际质量如下(单位:g)
甲:301,300,305,302,303,302,300,300,298,299
乙:305,302,300,300,300,300,298,299,301,305
(1)分别计算甲、乙这两个样本的平均数和方差;
(2)比较这两台包装机包装质量的稳定性.
19.为了调查甲,乙两台包装机分装标准质量为奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
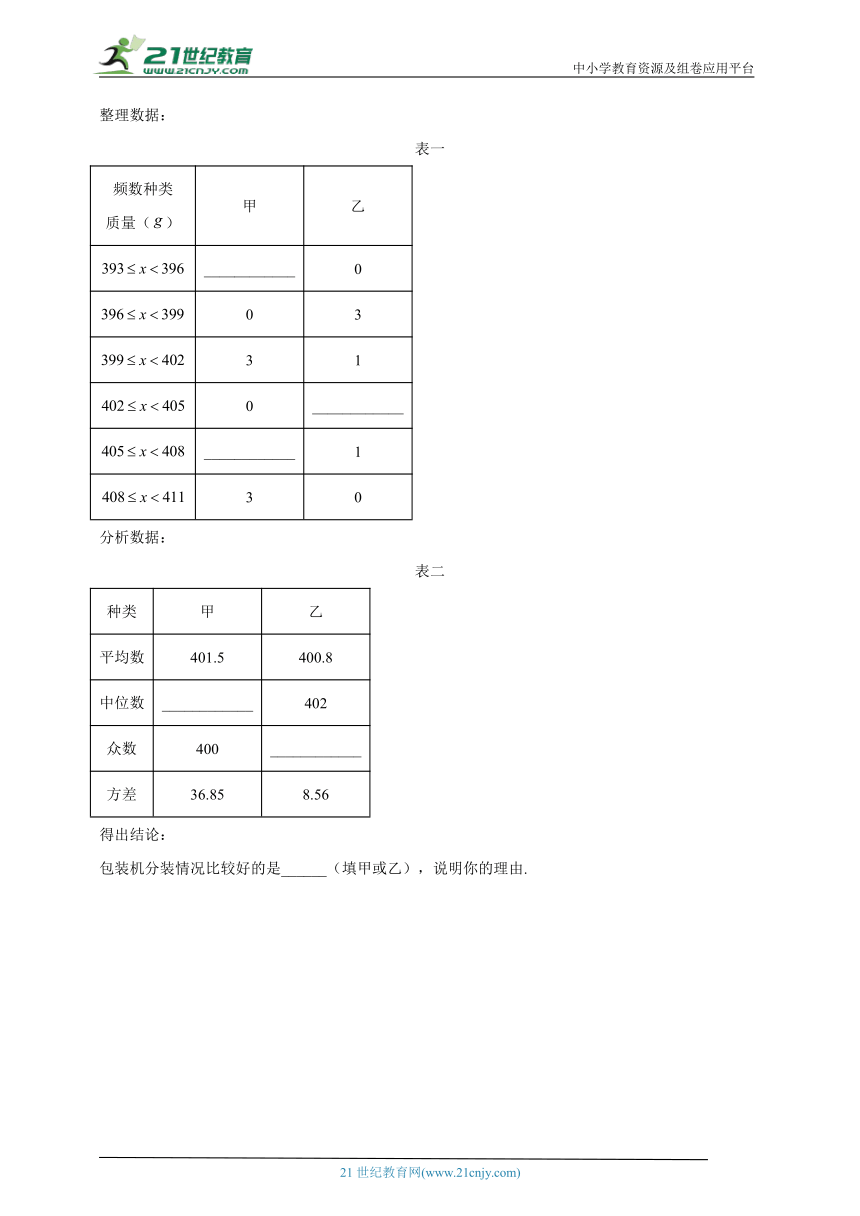
整理数据:
表一
频数种类 质量() 甲 乙
____________ 0
0 3
3 1
0 ____________
____________ 1
3 0
分析数据:
表二
种类 甲 乙
平均数 401.5 400.8
中位数 ____________ 402
众数 400 ____________
方差 36.85 8.56
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.
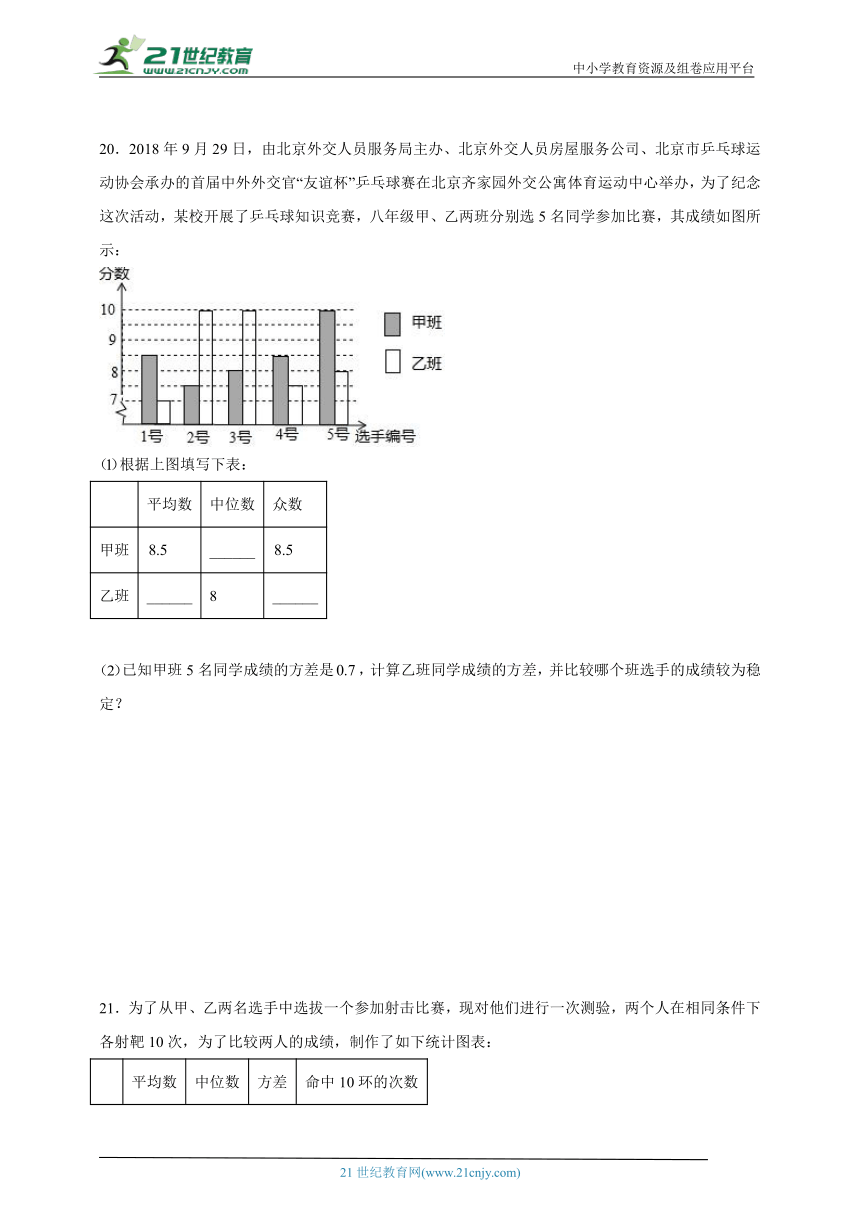
20.2018年9月29日,由北京外交人员服务局主办、北京外交人员房屋服务公司、北京市乒乓球运动协会承办的首届中外外交官“友谊杯”乒乓球赛在北京齐家园外交公寓体育运动中心举办,为了纪念这次活动,某校开展了乒乓球知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其成绩如图所示:
根据上图填写下表:
平均数 中位数 众数
甲班 ______
乙班 ______ 8 ______
已知甲班5名同学成绩的方差是,计算乙班同学成绩的方差,并比较哪个班选手的成绩较为稳定?
21.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
平均数 中位数 方差 命中10环的次数
甲 7 0
乙 7.5 5.4
甲、乙射击成绩折线图
(1)请补全上述图表(请直接在表中填空和补全折线图)
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由
22.八(6)班组织了一次经典朗读比赛,甲、乙两队各9人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 10 10 10
乙 10 8 7 9 8 10 10 9 10
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选 队.
23.已知直线分别与轴、轴交于点,点,点为这条直线上的点,轴于点,轴于点.
(1)①将下表中的空格填写完整:
1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6
6 5 4 3 2 1 0
4 4 4 4
②根据表格中的数据,下列判断正确的是 .
A. ,B. ,C..
(2)当点在第一象限时,解答下列问题:
①求证:矩形的周长是一个定值,并求这个定值;
②设矩形的面积为,求证:.
(3)当点在第四象限时,直接写出,满足的等式关系.
24.已知样本甲为a1、a2、a3样本乙为b1、b2、b3,若a1-b2=a2-b2=a3-b3,那么样本甲与样本乙的方差有什么关系,并证明你的结论.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D C D D C C D
题号 11 12
答案 A C
1.C
【分析】方差越小,成绩越稳定,据此判断即可.
【详解】解:∵0.43<0.90<1.22<1.68,∴丙成绩最稳定,
故选C
【点睛】本题考查了方差的相关知识,属于基础题型,掌握判断的方法是解题的关键.
2.D
【分析】本题考查方差的意义,根据方差越小,数据的波动越小,即可得到答案.
【详解】解:∵在统计中,方差可以近似的反映数据的波动程度,方差越大,数据的波动越大,
∴D选项符合方差定义.
故选:D.
3.D
【分析】根据方差的意义:是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.故要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生了10次短跑训练成绩的方差.
【详解】由于方差能反映数据的稳定性,需要比较这两名学生了10次短跑训练成绩的方差.
故选D.
【点睛】考查了统计量的选择,用到的知识点是方差的意义,掌握方差所表示的意义是解题的关键.
4.D
【分析】根据极差、中位数、众数和平均数的概念分别进行求解,即可得出答案.
【详解】、这组数据的极差是,正确;
、这组数据的平均数是,正确;
、这组数据的众数是,正确;
、这组数据的中位数是,错误.
故选.
【点睛】本题考查了极差、中位数、众数和平均数的知识,掌握各知识点的概念是解题的关键.
5.C
【详解】根据方差的意义:方差是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.同时,极差是最大与最小值的差,也反映波动越大小;故要判断谁的成绩更加稳定;一般要考查这5次成绩的方差或极差.
故选C.
6.D
【分析】根据方差的意义可作出判断,方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定;
【详解】每人10次射击成绩的平均数均是9.2环,方差依次为0.60、0.62、0.50、0.44,丁的方差最小,
成绩最稳定的是丁;
故选:D
【点睛】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.D
【分析】本题考查了平均数,众数,中位数,方差的定义,分别求出两组数据的平均数,众数,中位数,方差,进行比较即可.
【详解】解:原数据3、4、4、5,
平均数为,中位数为,众数为4,
方差为,
新数据3、4、4、4、5,
平均数为,中位数为,众数为4,
方差为,
,
则前后两组数据的统计量会变小的是方差,
故选:D.
8.C
【分析】根据数据的总个数以及1.50m和1.65m的人数和,可确定众数.
【详解】解:∵一共有21个数据,
∴1.50m和1.65m的人数和为21-(8+6+1)=6<8,
∴这组数据的众数为1.55m,
故选:C.
【点睛】本题主要考查数据分析的内容,掌握众数的概念是解题的关键.
9.C
【分析】根据众数,中位数,平均数、极差的定义解答即可.
【详解】解:由图可知,鹏鹏这一周睡眠时间这组数中出现7和8都是两次,所以众数是7和8.
把数据从小到大排列,中位数是第4个数,所以中位数是8.
平均数是(6+8+7+7+9+10+8)÷7=,所以平均数是.
最大为10,最小为6,极差为10-6=4,
故A、B、D错误,C正确.
故选:C.
【点睛】本题考查了折线统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键,也考查了极差、中位数、平均数、众数的相关知识.
10.D
【分析】根据方差的大小,可进行求解.
【详解】解:由题意得:;
∴应该派丁参加比赛更合适;
故选D.
【点睛】本题主要考查方差的意义,熟练掌握方差越小,数据越稳定是解题的关键.
11.A
【分析】本题主要考查方差,熟练掌握方差是解题的关键;此题可根据方差的性质“方差越小,数据的波动越小”进行求解.
【详解】解:∵,
∴甲更稳定,
故选A.
12.C
【分析】分别求出样本容量、中位数、众数、方差后,即可做出判断.
【详解】A.由题意可知,样本容量为,故选项错误,不符合题意;
B.由题意可知,该组数据共有10个,处在中间的两个都是300,故中位数为,故选项错误,不符合题意;
C.该组数据出现次数最多的是300,共出现5次,故众数为300,故选项正确,符合题意;
D.由题意可得,平均数,
方差为,
故选项错误,不符合题意.
故选:C.
【点睛】此题考查了样本容量、中位数、众数、方差等知识点,熟练掌握各统计量的求法是解题的关键.
13.cm
【分析】先计算出四个数据的平均数,再代入方差的公式计算求值.
【详解】∵(176+174+177+173)=175(cm),∴S2[(176﹣175)2+(174﹣175)2+(177﹣175)2+(173﹣175)2](1+1+4+4)(cm2).
故答案为cm2.
【点睛】本题考查了方差的计算.若n个数据x1,x2,…xn的平均数为,则方差S2[(x1)2+(x2)2+…+(xn)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.丙
【分析】根据方差表示数据的波动大小的量即可解答.
【详解】解:∵平均成绩都是87.9分,s甲2=3.83,s乙2=2.71,s丙2=1.52,
∴s丙2<s乙2<s甲2,
∴选手丙的成绩更稳定,即适合参加比赛的选手是丙.
故答案为:丙.
【点睛】本题考查了方差的意义,理解方差是表示数据波动大小的量是解答本题的关键.
15..
【详解】已知数据0,1,2,2,x,3的平均数是2,
由平均数的公式计算可得(0+1+2+2+x+3)÷6=2,
解得x=4,
再根据方差的公式可得,
这组数据的方差= [(2﹣0)2+(2﹣1)2+(2﹣2)2+(2﹣2)2+(2﹣4)2+(2﹣3)2]=.
16.7
【分析】先计算出样本的极差,再除以组距,最后向上一位取整即可得出组数.
【详解】解:∵样本最大值为127,最小值为60,
∴极差为127﹣60=67,
∵组距为10,
∴67÷10=6.7,
∴此样本可分成7组,
故答案为:7.
【点睛】本题考查频数分布表中组数的确定,关键是求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
17.2
【分析】先根据平均数的定义确定平均数,再根据方差公式进行计算即可求出答案.
【详解】这组数据的平均数是:,
则方差;
故答案为2.
【点睛】此题考查方差,解题关键在于掌握方差的计算公式.
18.(1)甲平均数301,乙平均数301,甲方差3.2,乙方差4.2;(2)甲包装机包装质量的稳定性好,见解析
【分析】(1)根据平均数就是对每组数求和后除以数的个数;根据方差公式计算即可;
(2)方差大说明这组数据波动大,方差小则波动小,就比较稳定.依此判断即可.
【详解】解:(1)=(1+0+5+2+3+2+0+0﹣2﹣1)+300=301,
=(5+2+0+0+0+0﹣2﹣1+1+5)+300=301,
=[(301﹣301)2+(301﹣300)2+(301﹣305)2+(301﹣302)2+(301﹣303)2+(301﹣302)2+(301﹣300)2+(301﹣300)2+(301﹣298)2+(301﹣299)2]=3.2;
=[(301﹣305)2+(301﹣302)2+(301﹣300)2+(301﹣300)2+(301﹣300)2+(301﹣300)2+(301﹣298)2+(301﹣299)2+(301﹣301)2+(301﹣305)2]=4.2;
(2)∵<,
∴甲包装机包装质量的稳定性好.
【点睛】本题考查了平均数和方差,正确掌握平均数及方差的求解公式是解题的关键.
19.整理数据:3,1,5;分析数据:400,402;得出结论:乙,理由详见解析.
【分析】整理数据:根据所给的数据填写表格一即可;分析数据:根据中位数、众数的定义求解即可;得出结论:结合表二中的数据解答即可.
【详解】整理数据:
表一中,
甲组:393≤x<396的有3个,405≤x<408的有1个;
乙组:402≤x<405的有5个;
故答案为3,1,5;
分析数据:
表二中,
甲组:把10个数据按照从小到大顺序排列为:393,394,395,400,400,400,406,408,409,410,
中位数为中间两个数据的平均数==400,
乙组:出现次数最多的数据是402,
∴众数是402;
故答案为400,402;
得出结论:
包装机分装情况比较好的是乙;理由如下:
由表二知,乙包装机分装的奶粉质量的方差小,分装质量比较稳定,
所以包装机分装情况比较好的是乙.
故答案为乙(答案不唯一,合理即可).
【点睛】本题考查了众数、中位数以及方差,掌握众数、中位数以及方差的定义及数据的整理是解题的关键.
20.(1),,10;(2)甲班.
【分析】(1)把甲班5名同学的成绩从小到大排列,找出最中间的数即可求出甲班的中位数,根据平均数的计算公式列出算式,求出乙班5名同学的成绩的平均数,找出乙班出现的次数最多的数即可求出乙班的众数.
(2)求出乙班同学的方差再与甲班5名同学成绩的方差比较即可.
【详解】(1)把甲班5名同学的成绩从小到大排列为:7.5,8,8.5,8.5,10,最中间的数是8.5,则甲班的中位数是8.5,乙班5名同学的成绩的平均数是(7+10+10+7.5+8)÷5=8.5,10出现的次数最多,则乙班的众数是10.
故答案为8.5,8.5,10.
(2)乙班同学的方差为:[(7﹣8.5)2+2×(10﹣8.5)2+(7.5﹣8.5)2+(8﹣8.5)2]=1.6.
∵甲班5名同学成绩的方差是0.7,0.7<1.6,∴甲班选手的成绩较为稳定.
【点睛】本题考查了方差、中位数、众数、平均数,关键是熟练掌握了方差、中位数、众数、平均数的概念和计算方法.
21.(1)见解析
(2)甲胜出,方差小,见解析
【分析】(1)分别利用中位数以及方差和平均数求法得出即可;
(2)根据(1)计算出的甲乙两人的方差,比较大小即可做出判断.
【详解】(1)根据折线统计图得:
乙的射击成绩为:2,4,6,8,7,7,8,9,9,10,
则平均数为:×(2+4+6+8+7+7+8+9+9+10)=7(环),
甲的射击成绩为9,6,7,6,5,7,7,?,8,9,平均数为7环,
则甲第八环成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),
所以甲的10次成绩为:9,6,7,6,5,7,7,6,8,9,
把这些数从小到大排列为5,6,6,6,7,7,7,8,9,9,
则中位数是:=7(环),
甲的方差为:;
乙命中10环的次数为1.
补统计表如下:
平均数 中位数 方差 命中10环的次数
甲 7 7 1.6 0
乙 7 7.5 5.4 1
补全折线统计图如下:
(2)由甲的方差小于乙的方差,甲比较稳定,故甲胜出.
【点睛】此题考查了折线统计图,中位数,方差,平均数,以及统计表,掌握相关统计量的计算方法是解本题的关键.
22.(1)10,9;(2)1;(3)乙.
【详解】试题分析:本题考查方差、中位数、众数等众数,记住这些知识是解决问题的关键,方差越小成绩越稳定,属于中考常考题型.
(1)根据中位数的定义即可解决.
(2)根据平均数、方差公式计算即可.
(3)根据方差越小成绩越稳定作出判断.
试题解析:(1)甲队成绩的中位数是10分,乙队成绩的中位数分9.
故答案分别为10,9.
(2)==9.
s乙2=[(10-9)2+(8-9)2+(7-9)2+(9-9)2+(8-9)2+(10-9)2+(10-9)2+(9-9)2+(10-9)2]=1,
(3)∵s甲2=,s乙2=1,
∴s乙2<s甲2,
∴乙的成绩稳定,选乙队.
故答案为乙.
考点:1.方差;2.中位数;3.众数.
23.(1)①4,4,4,4,4;②A、B、C;(2)①矩形的周长是一个定值,周长为8;②见解析;(3)
【分析】(1)①把表中对应的值相加即可完成;
②根据数据的平均数和方差计算公式计算即可;
(2)①设点Q的坐标为,由点Q在第一象限,则,,从而可求得矩形OPQR的周长,且可知周长为定值;
②计算4-S,并判断其符号即可;
(3)设点Q的坐标为,由点Q在第四象限,则,,则的关系.
【详解】(1)①填表如下:
1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6
6 5 4 3 2 1 0
4 4 4 4 4 4 4 4 4
②,故A正确;
∴,故B正确;
∵
∴
故C正确;
故答案为:A、B、C
(2)①设,
∵点在第一象限,
∴,,
∴,
∴矩形的周长是一个定值,周长为8;
②∵
∴.
(3)设点Q的坐标为,
∵点Q在第四象限,
∴,,
∴.
【点睛】本题考查了数据的平均数、方差,点在直线上的坐标特征,图形的面积与周长,各象限点的坐标特点等知识,掌握这些知识是解答本题的关键.同时要注意,点的坐标与点到两坐标轴的距离既有联系又有区别.
24.相等,证明详见解析.
【分析】样本甲与样本乙的方差相等,设a1-b2=a2-b2=a3-b3=k,则a1=b2+k,a2=b2+k,a3=b3+k,根据将一组数据中每个数据的值都加上(或减去)同一个常数,这组数据的波动大小不变,方差不变即可证明结论.
【详解】样本甲与样本乙的方差相等,
证明:设a1-b2=a2-b2=a3-b3=k,则a1=b2+k,a2=b2+k,a3=b3+k,
∴样本甲的数据可以看作样本乙的每一个数据加k,
∵将一组数据中每个数据的值都加上(或减去)同一个常数,这组数据的波动大小不变,方差不变,
∴样本甲与样本乙的方差相等.
【点睛】本题考查了方差公式的运用,熟知将一组数据中每个数据的值都加上(或减去)同一个常数,这组数据的波动大小不变,方差不变是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
20.2数据的波动程度
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,
方差分别是,,,.在本次射击测试中,成绩最
稳定的是( )
A.甲 B.乙 C.丙 D.丁
2.在统计中,样本的方差可以近似的反映总体的( )
A.最大值与最小值 B.平均状态
C.分布规律 D.波动大小
3.体育课上,某班两名同学分别进行10次短跑训练,要判断哪一名同学的成绩比较稳定,通常需要比较这两名学生成绩的( )
A.平均数 B.众数 C.中位数 D.方差
4.在2017年的初中数学竞赛中,我校有5位同学获奖,他们的成绩分别是88,86,91,88,92.则由这组数据得到的以下结论,错误的是( )
A.极差为6 B.平均数为89 C.众数为88 D.中位数为91
5.教练组对运动员正式比赛前的5次训练成绩进行分析,判断谁的成绩更加稳定,一般需要考察这5次成绩的 ( )
A.平均数或中位数 B.众数或频率 C.方差或极差 D.频数或众数
6.甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,据此分析,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )
统计量 甲 乙 丙 丁
平均数 9.2 9.1 9.3 9.1
方差 0.60 0.62 0.50 0.44
A.甲 B.乙 C.丙 D.丁
7.一组数据3、4、4、5,若添加一个数4得到一组新数据,则前后两组数据的统计量会变小的是( )
A.平均数 B.中位数 C.众数 D.方差
8.一次中学生田径运动会上,21名参加男子跳高项目的运动员成绩统计如下:
成绩(m) 1.50 1.55 1.60 1.65 1.70
人数 ■ 8 6 ■ 1
其中有两个数据被雨水淋湿模糊不清了,则在这组数据中能确定的统计量是()
A.平均数 B.中位数 C.众数 D.方差
9.初中生每天的睡眠时间应为9个小时.鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则下列说法正确的是( )
A.鹏鹏这一周睡眠时间的中位数是7小时
B.鹏鹏这一周睡眠时间的众数是7小时
C.鹏鹏这一周睡眠时间的极差是4小时
D.鹏鹏这一周睡眠时间的平均数是8小时
10.从甲、乙、丙、丁四人中选出一人参加射击比赛,经过初赛统计,他们的平均成绩都是9环,方差分别是,,,,结合以上数据,你认为派谁参加比赛更合适( )
A.甲 B.乙 C.丙 D.丁
11.甲、乙两位同学进行“汉字拼写”训练,他们5次训练成绩的平均数均为90分,方差分别为,,则下列对两位同学成绩的稳定性描述正确的是( )
A.甲更稳定 B.乙更稳定 C.一样稳定 D.无法确定
12.某奶茶小店某月每日营业额(单位:元)中随机抽取部分数据,根据方差公式,得则下列说法正确的是( )
A.样本的容量是4 B.该组数据的中位数是400
C.该组数据的众数是300 D.
二、填空题
13.学完方差的知识后,小明了解了他最要好的四个朋友的身高,分别是176cm,174cm,177cm,173cm,那么小明四个好朋友身高的方差是 .
14.从甲、乙、丙三人中选拔一人参加职业技能大赛,经过几轮初赛选拔,他们的平均成绩都是87.9分,方差分别是s甲2=3.83,s乙2=2.71,s丙2=1.52.若选取成绩稳定的一人参加比赛,你认为适合参加比赛的选手是 .
15.已知一组数据0,1,2,2,x,3的平均数是2,则这组数据的方差是 .
16.一个样本容量为50的样本最大值为127,最小值为60,组距为10,则可分成 组.
17.一组数据为0,1,2,3,4,则这组数据的方差是 .
三、解答题
18.从甲、乙两台包装机包装的质量为300g的袋装食品中各抽取10袋,测得其实际质量如下(单位:g)
甲:301,300,305,302,303,302,300,300,298,299
乙:305,302,300,300,300,300,298,299,301,305
(1)分别计算甲、乙这两个样本的平均数和方差;
(2)比较这两台包装机包装质量的稳定性.
19.为了调查甲,乙两台包装机分装标准质量为奶粉的情况,质检员进行了抽样调查,过程如下.请补全表一、表二中的空,并回答提出的问题.
收集数据:
从甲、乙包装机分装的奶粉中各自随机抽取10袋,测得实际质量(单位:)如下:
甲:394,400,408,406,410,409,400,400,393,395
乙:402,404,396,403,402,405,397,399,402,398
整理数据:
表一
频数种类 质量() 甲 乙
____________ 0
0 3
3 1
0 ____________
____________ 1
3 0
分析数据:
表二
种类 甲 乙
平均数 401.5 400.8
中位数 ____________ 402
众数 400 ____________
方差 36.85 8.56
得出结论:
包装机分装情况比较好的是______(填甲或乙),说明你的理由.
20.2018年9月29日,由北京外交人员服务局主办、北京外交人员房屋服务公司、北京市乒乓球运动协会承办的首届中外外交官“友谊杯”乒乓球赛在北京齐家园外交公寓体育运动中心举办,为了纪念这次活动,某校开展了乒乓球知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其成绩如图所示:
根据上图填写下表:
平均数 中位数 众数
甲班 ______
乙班 ______ 8 ______
已知甲班5名同学成绩的方差是,计算乙班同学成绩的方差,并比较哪个班选手的成绩较为稳定?
21.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
平均数 中位数 方差 命中10环的次数
甲 7 0
乙 7.5 5.4
甲、乙射击成绩折线图
(1)请补全上述图表(请直接在表中填空和补全折线图)
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由
22.八(6)班组织了一次经典朗读比赛,甲、乙两队各9人的比赛成绩如下表(10分制):
甲 7 8 9 7 10 10 10 10 10
乙 10 8 7 9 8 10 10 9 10
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选 队.
23.已知直线分别与轴、轴交于点,点,点为这条直线上的点,轴于点,轴于点.
(1)①将下表中的空格填写完整:
1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6
6 5 4 3 2 1 0
4 4 4 4
②根据表格中的数据,下列判断正确的是 .
A. ,B. ,C..
(2)当点在第一象限时,解答下列问题:
①求证:矩形的周长是一个定值,并求这个定值;
②设矩形的面积为,求证:.
(3)当点在第四象限时,直接写出,满足的等式关系.
24.已知样本甲为a1、a2、a3样本乙为b1、b2、b3,若a1-b2=a2-b2=a3-b3,那么样本甲与样本乙的方差有什么关系,并证明你的结论.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D C D D C C D
题号 11 12
答案 A C
1.C
【分析】方差越小,成绩越稳定,据此判断即可.
【详解】解:∵0.43<0.90<1.22<1.68,∴丙成绩最稳定,
故选C
【点睛】本题考查了方差的相关知识,属于基础题型,掌握判断的方法是解题的关键.
2.D
【分析】本题考查方差的意义,根据方差越小,数据的波动越小,即可得到答案.
【详解】解:∵在统计中,方差可以近似的反映数据的波动程度,方差越大,数据的波动越大,
∴D选项符合方差定义.
故选:D.
3.D
【分析】根据方差的意义:是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.故要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生了10次短跑训练成绩的方差.
【详解】由于方差能反映数据的稳定性,需要比较这两名学生了10次短跑训练成绩的方差.
故选D.
【点睛】考查了统计量的选择,用到的知识点是方差的意义,掌握方差所表示的意义是解题的关键.
4.D
【分析】根据极差、中位数、众数和平均数的概念分别进行求解,即可得出答案.
【详解】、这组数据的极差是,正确;
、这组数据的平均数是,正确;
、这组数据的众数是,正确;
、这组数据的中位数是,错误.
故选.
【点睛】本题考查了极差、中位数、众数和平均数的知识,掌握各知识点的概念是解题的关键.
5.C
【详解】根据方差的意义:方差是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.同时,极差是最大与最小值的差,也反映波动越大小;故要判断谁的成绩更加稳定;一般要考查这5次成绩的方差或极差.
故选C.
6.D
【分析】根据方差的意义可作出判断,方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定;
【详解】每人10次射击成绩的平均数均是9.2环,方差依次为0.60、0.62、0.50、0.44,丁的方差最小,
成绩最稳定的是丁;
故选:D
【点睛】本题考查方差的意义,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7.D
【分析】本题考查了平均数,众数,中位数,方差的定义,分别求出两组数据的平均数,众数,中位数,方差,进行比较即可.
【详解】解:原数据3、4、4、5,
平均数为,中位数为,众数为4,
方差为,
新数据3、4、4、4、5,
平均数为,中位数为,众数为4,
方差为,
,
则前后两组数据的统计量会变小的是方差,
故选:D.
8.C
【分析】根据数据的总个数以及1.50m和1.65m的人数和,可确定众数.
【详解】解:∵一共有21个数据,
∴1.50m和1.65m的人数和为21-(8+6+1)=6<8,
∴这组数据的众数为1.55m,
故选:C.
【点睛】本题主要考查数据分析的内容,掌握众数的概念是解题的关键.
9.C
【分析】根据众数,中位数,平均数、极差的定义解答即可.
【详解】解:由图可知,鹏鹏这一周睡眠时间这组数中出现7和8都是两次,所以众数是7和8.
把数据从小到大排列,中位数是第4个数,所以中位数是8.
平均数是(6+8+7+7+9+10+8)÷7=,所以平均数是.
最大为10,最小为6,极差为10-6=4,
故A、B、D错误,C正确.
故选:C.
【点睛】本题考查了折线统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键,也考查了极差、中位数、平均数、众数的相关知识.
10.D
【分析】根据方差的大小,可进行求解.
【详解】解:由题意得:;
∴应该派丁参加比赛更合适;
故选D.
【点睛】本题主要考查方差的意义,熟练掌握方差越小,数据越稳定是解题的关键.
11.A
【分析】本题主要考查方差,熟练掌握方差是解题的关键;此题可根据方差的性质“方差越小,数据的波动越小”进行求解.
【详解】解:∵,
∴甲更稳定,
故选A.
12.C
【分析】分别求出样本容量、中位数、众数、方差后,即可做出判断.
【详解】A.由题意可知,样本容量为,故选项错误,不符合题意;
B.由题意可知,该组数据共有10个,处在中间的两个都是300,故中位数为,故选项错误,不符合题意;
C.该组数据出现次数最多的是300,共出现5次,故众数为300,故选项正确,符合题意;
D.由题意可得,平均数,
方差为,
故选项错误,不符合题意.
故选:C.
【点睛】此题考查了样本容量、中位数、众数、方差等知识点,熟练掌握各统计量的求法是解题的关键.
13.cm
【分析】先计算出四个数据的平均数,再代入方差的公式计算求值.
【详解】∵(176+174+177+173)=175(cm),∴S2[(176﹣175)2+(174﹣175)2+(177﹣175)2+(173﹣175)2](1+1+4+4)(cm2).
故答案为cm2.
【点睛】本题考查了方差的计算.若n个数据x1,x2,…xn的平均数为,则方差S2[(x1)2+(x2)2+…+(xn)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
14.丙
【分析】根据方差表示数据的波动大小的量即可解答.
【详解】解:∵平均成绩都是87.9分,s甲2=3.83,s乙2=2.71,s丙2=1.52,
∴s丙2<s乙2<s甲2,
∴选手丙的成绩更稳定,即适合参加比赛的选手是丙.
故答案为:丙.
【点睛】本题考查了方差的意义,理解方差是表示数据波动大小的量是解答本题的关键.
15..
【详解】已知数据0,1,2,2,x,3的平均数是2,
由平均数的公式计算可得(0+1+2+2+x+3)÷6=2,
解得x=4,
再根据方差的公式可得,
这组数据的方差= [(2﹣0)2+(2﹣1)2+(2﹣2)2+(2﹣2)2+(2﹣4)2+(2﹣3)2]=.
16.7
【分析】先计算出样本的极差,再除以组距,最后向上一位取整即可得出组数.
【详解】解:∵样本最大值为127,最小值为60,
∴极差为127﹣60=67,
∵组距为10,
∴67÷10=6.7,
∴此样本可分成7组,
故答案为:7.
【点睛】本题考查频数分布表中组数的确定,关键是求出最大值和最小值的差,然后除以组距,用进一法取整数值就是组数.
17.2
【分析】先根据平均数的定义确定平均数,再根据方差公式进行计算即可求出答案.
【详解】这组数据的平均数是:,
则方差;
故答案为2.
【点睛】此题考查方差,解题关键在于掌握方差的计算公式.
18.(1)甲平均数301,乙平均数301,甲方差3.2,乙方差4.2;(2)甲包装机包装质量的稳定性好,见解析
【分析】(1)根据平均数就是对每组数求和后除以数的个数;根据方差公式计算即可;
(2)方差大说明这组数据波动大,方差小则波动小,就比较稳定.依此判断即可.
【详解】解:(1)=(1+0+5+2+3+2+0+0﹣2﹣1)+300=301,
=(5+2+0+0+0+0﹣2﹣1+1+5)+300=301,
=[(301﹣301)2+(301﹣300)2+(301﹣305)2+(301﹣302)2+(301﹣303)2+(301﹣302)2+(301﹣300)2+(301﹣300)2+(301﹣298)2+(301﹣299)2]=3.2;
=[(301﹣305)2+(301﹣302)2+(301﹣300)2+(301﹣300)2+(301﹣300)2+(301﹣300)2+(301﹣298)2+(301﹣299)2+(301﹣301)2+(301﹣305)2]=4.2;
(2)∵<,
∴甲包装机包装质量的稳定性好.
【点睛】本题考查了平均数和方差,正确掌握平均数及方差的求解公式是解题的关键.
19.整理数据:3,1,5;分析数据:400,402;得出结论:乙,理由详见解析.
【分析】整理数据:根据所给的数据填写表格一即可;分析数据:根据中位数、众数的定义求解即可;得出结论:结合表二中的数据解答即可.
【详解】整理数据:
表一中,
甲组:393≤x<396的有3个,405≤x<408的有1个;
乙组:402≤x<405的有5个;
故答案为3,1,5;
分析数据:
表二中,
甲组:把10个数据按照从小到大顺序排列为:393,394,395,400,400,400,406,408,409,410,
中位数为中间两个数据的平均数==400,
乙组:出现次数最多的数据是402,
∴众数是402;
故答案为400,402;
得出结论:
包装机分装情况比较好的是乙;理由如下:
由表二知,乙包装机分装的奶粉质量的方差小,分装质量比较稳定,
所以包装机分装情况比较好的是乙.
故答案为乙(答案不唯一,合理即可).
【点睛】本题考查了众数、中位数以及方差,掌握众数、中位数以及方差的定义及数据的整理是解题的关键.
20.(1),,10;(2)甲班.
【分析】(1)把甲班5名同学的成绩从小到大排列,找出最中间的数即可求出甲班的中位数,根据平均数的计算公式列出算式,求出乙班5名同学的成绩的平均数,找出乙班出现的次数最多的数即可求出乙班的众数.
(2)求出乙班同学的方差再与甲班5名同学成绩的方差比较即可.
【详解】(1)把甲班5名同学的成绩从小到大排列为:7.5,8,8.5,8.5,10,最中间的数是8.5,则甲班的中位数是8.5,乙班5名同学的成绩的平均数是(7+10+10+7.5+8)÷5=8.5,10出现的次数最多,则乙班的众数是10.
故答案为8.5,8.5,10.
(2)乙班同学的方差为:[(7﹣8.5)2+2×(10﹣8.5)2+(7.5﹣8.5)2+(8﹣8.5)2]=1.6.
∵甲班5名同学成绩的方差是0.7,0.7<1.6,∴甲班选手的成绩较为稳定.
【点睛】本题考查了方差、中位数、众数、平均数,关键是熟练掌握了方差、中位数、众数、平均数的概念和计算方法.
21.(1)见解析
(2)甲胜出,方差小,见解析
【分析】(1)分别利用中位数以及方差和平均数求法得出即可;
(2)根据(1)计算出的甲乙两人的方差,比较大小即可做出判断.
【详解】(1)根据折线统计图得:
乙的射击成绩为:2,4,6,8,7,7,8,9,9,10,
则平均数为:×(2+4+6+8+7+7+8+9+9+10)=7(环),
甲的射击成绩为9,6,7,6,5,7,7,?,8,9,平均数为7环,
则甲第八环成绩为70-(9+6+7+6+5+7+7+8+9)=6(环),
所以甲的10次成绩为:9,6,7,6,5,7,7,6,8,9,
把这些数从小到大排列为5,6,6,6,7,7,7,8,9,9,
则中位数是:=7(环),
甲的方差为:;
乙命中10环的次数为1.
补统计表如下:
平均数 中位数 方差 命中10环的次数
甲 7 7 1.6 0
乙 7 7.5 5.4 1
补全折线统计图如下:
(2)由甲的方差小于乙的方差,甲比较稳定,故甲胜出.
【点睛】此题考查了折线统计图,中位数,方差,平均数,以及统计表,掌握相关统计量的计算方法是解本题的关键.
22.(1)10,9;(2)1;(3)乙.
【详解】试题分析:本题考查方差、中位数、众数等众数,记住这些知识是解决问题的关键,方差越小成绩越稳定,属于中考常考题型.
(1)根据中位数的定义即可解决.
(2)根据平均数、方差公式计算即可.
(3)根据方差越小成绩越稳定作出判断.
试题解析:(1)甲队成绩的中位数是10分,乙队成绩的中位数分9.
故答案分别为10,9.
(2)==9.
s乙2=[(10-9)2+(8-9)2+(7-9)2+(9-9)2+(8-9)2+(10-9)2+(10-9)2+(9-9)2+(10-9)2]=1,
(3)∵s甲2=,s乙2=1,
∴s乙2<s甲2,
∴乙的成绩稳定,选乙队.
故答案为乙.
考点:1.方差;2.中位数;3.众数.
23.(1)①4,4,4,4,4;②A、B、C;(2)①矩形的周长是一个定值,周长为8;②见解析;(3)
【分析】(1)①把表中对应的值相加即可完成;
②根据数据的平均数和方差计算公式计算即可;
(2)①设点Q的坐标为,由点Q在第一象限,则,,从而可求得矩形OPQR的周长,且可知周长为定值;
②计算4-S,并判断其符号即可;
(3)设点Q的坐标为,由点Q在第四象限,则,,则的关系.
【详解】(1)①填表如下:
1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6
6 5 4 3 2 1 0
4 4 4 4 4 4 4 4 4
②,故A正确;
∴,故B正确;
∵
∴
故C正确;
故答案为:A、B、C
(2)①设,
∵点在第一象限,
∴,,
∴,
∴矩形的周长是一个定值,周长为8;
②∵
∴.
(3)设点Q的坐标为,
∵点Q在第四象限,
∴,,
∴.
【点睛】本题考查了数据的平均数、方差,点在直线上的坐标特征,图形的面积与周长,各象限点的坐标特点等知识,掌握这些知识是解答本题的关键.同时要注意,点的坐标与点到两坐标轴的距离既有联系又有区别.
24.相等,证明详见解析.
【分析】样本甲与样本乙的方差相等,设a1-b2=a2-b2=a3-b3=k,则a1=b2+k,a2=b2+k,a3=b3+k,根据将一组数据中每个数据的值都加上(或减去)同一个常数,这组数据的波动大小不变,方差不变即可证明结论.
【详解】样本甲与样本乙的方差相等,
证明:设a1-b2=a2-b2=a3-b3=k,则a1=b2+k,a2=b2+k,a3=b3+k,
∴样本甲的数据可以看作样本乙的每一个数据加k,
∵将一组数据中每个数据的值都加上(或减去)同一个常数,这组数据的波动大小不变,方差不变,
∴样本甲与样本乙的方差相等.
【点睛】本题考查了方差公式的运用,熟知将一组数据中每个数据的值都加上(或减去)同一个常数,这组数据的波动大小不变,方差不变是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
