20.3课题学习体质健康测试中的数据分析同步练习(含解析)
文档属性
| 名称 | 20.3课题学习体质健康测试中的数据分析同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 897.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 17:33:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
20.3课题学习体质健康测试中的数据分析
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价 元 元 元 元
数目 本 本 本 本
下列说法正确的是( )
A.该班级所售图书的总收入是元 B.在该班级所传图书价格组成的一组数据中,中位数是元
C.在该班级所售图书价格组成的一组数据中,众数是元 D.在该班级所售图书价格组成的一组数据中,平均数是元
2.某班40名学生右眼视力的检查结果如下表所示:
视力 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2
人数 1 2 3 2 3 4 4 6 10 4 1
这组数据的众数和中位数分别是( )
A.5.0,4.7 B.4.9,4.9 C.4.9,4.7 D.5.0,4.9
3.在刚刚结束的中考英语听力、口语测试中,某班口语成绩情况如图所示,则下列说法正确的是( )
A.中位数是9 B.众数为16 C.平均分为7.78 D.方差为2
4.下表是食品营养成分表的一部分(每100克食品中可食部分营养成分的含量)
蔬菜种类 绿豆芽 白 菜 油 菜 卷心菜 菠 菜 韭 菜 胡萝卜(红)
碳水化合物(克) 4 3 4 4 2 4 7
在表中提供的碳水化合物的克数所组成的数据中,中位数,平均数是( )
A.3 ;5 B.4 ;4 C.2 ;3 D.3;7
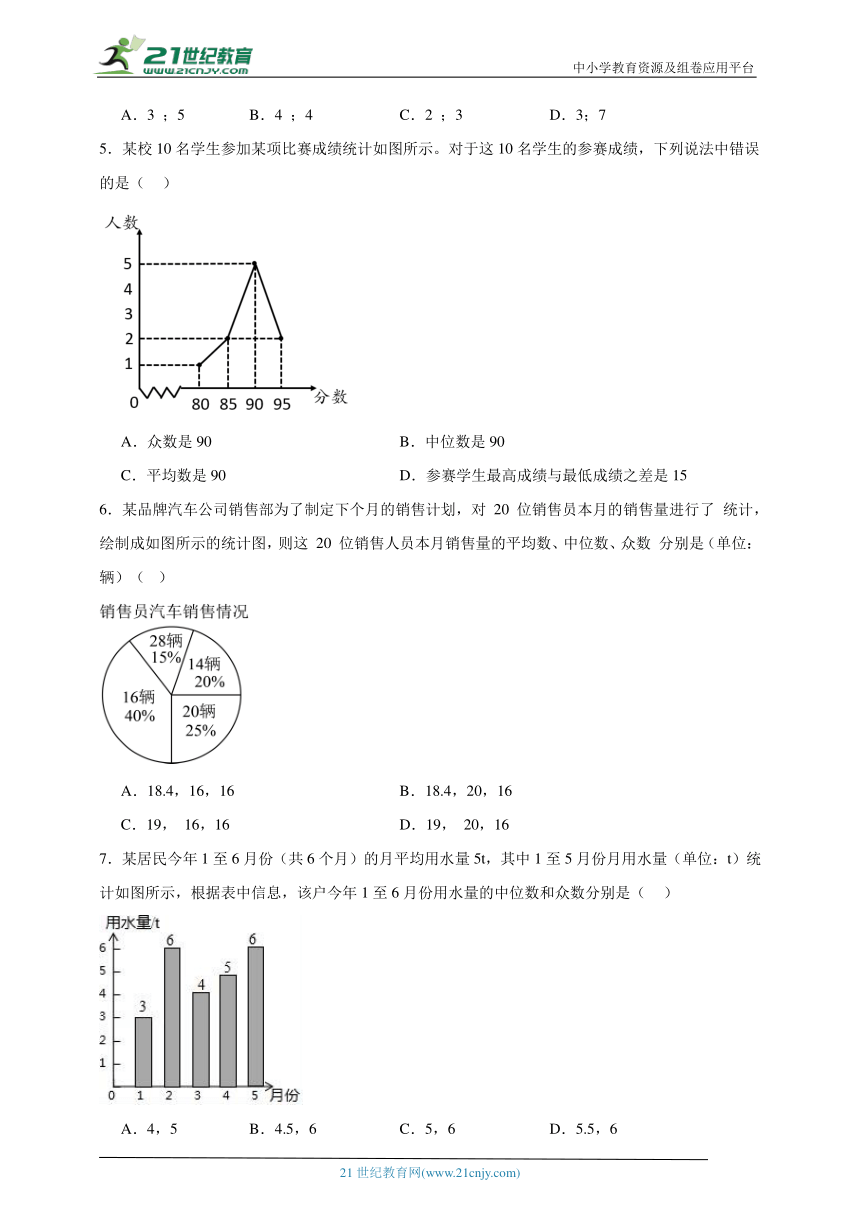
5.某校10名学生参加某项比赛成绩统计如图所示。对于这10名学生的参赛成绩,下列说法中错误的是( )
A.众数是90 B.中位数是90
C.平均数是90 D.参赛学生最高成绩与最低成绩之差是15
6.某品牌汽车公司销售部为了制定下个月的销售计划,对 20 位销售员本月的销售量进行了 统计,绘制成如图所示的统计图,则这 20 位销售人员本月销售量的平均数、中位数、众数 分别是(单位:辆)( )
A.18.4,16,16 B.18.4,20,16
C.19, 16,16 D.19, 20,16
7.某居民今年1至6月份(共6个月)的月平均用水量5t,其中1至5月份月用水量(单位:t)统计如图所示,根据表中信息,该户今年1至6月份用水量的中位数和众数分别是( )
A.4,5 B.4.5,6 C.5,6 D.5.5,6
8.为了了解阳光居民小区“全民健身”活动的开展情况,某志愿者随机调查了该小区50名成年居民一周的体育锻炼时间,并将数据进行整理后绘制成如图所示的统计图,则这50人一周体育锻炼时间的众数是( )
A.6小时 B.20人 C.10小时 D.3人
9.如图是根据某地4月上旬每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是( ).
A.5° 5° 4° B.5° 5° 4.5° C.2.8° 5° 4° D.2.8° 5° 4.5°
10.一组学生的身高是(单位:米),则这组学生身高数据的极差是( )
A.2 B. C. D.0
11.李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间(小时) 2 2.5 3 3.5 4
学生人数(名) 1 2 8 6 3
则关于这20名学生阅读小时数的说法正确的是( )
A.众数是8 B.中位数是3
C.平均数是3 D.方差是0.34
12.某学校七年级1班统计了全班同学在1~8月份的课外阅读数量(单位:本),绘制了右边的折线统计图,下列说法正确的是( )
A.极差是47 B.中位数是58 C.众数是42 D.极差大于平均数
二、填空题
13.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是 ,众数是 ,中位数是 .
14.某校901班共有50名同学,如图是该次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数),则测试成绩的中位数所在的组别是 .
15.样本数据3,6,a,4,2的平均数是5,则这个样本的方差是
16.某生产线在同一时间只能生产一笔订单,即在完成一笔订单后才能开始生产下一笔订单中的产品.一笔订单的“相对等待时间”定义为该笔订单的等待时间与生产线完成该订单所需时间之比.例如,该生产线完成第一笔订单用时5小时,之后完成第二笔订单用时2小时,则第一笔订单的“相对等待时间”为0,第二笔订单的“相对等待时间”为.现有甲、乙、丙三笔订单管理员估测这三笔订单的生产时间(单位:小时)依次为a,b,c,其中,则使三笔订单“相对等待时间”之和最小的生产顺序是 .
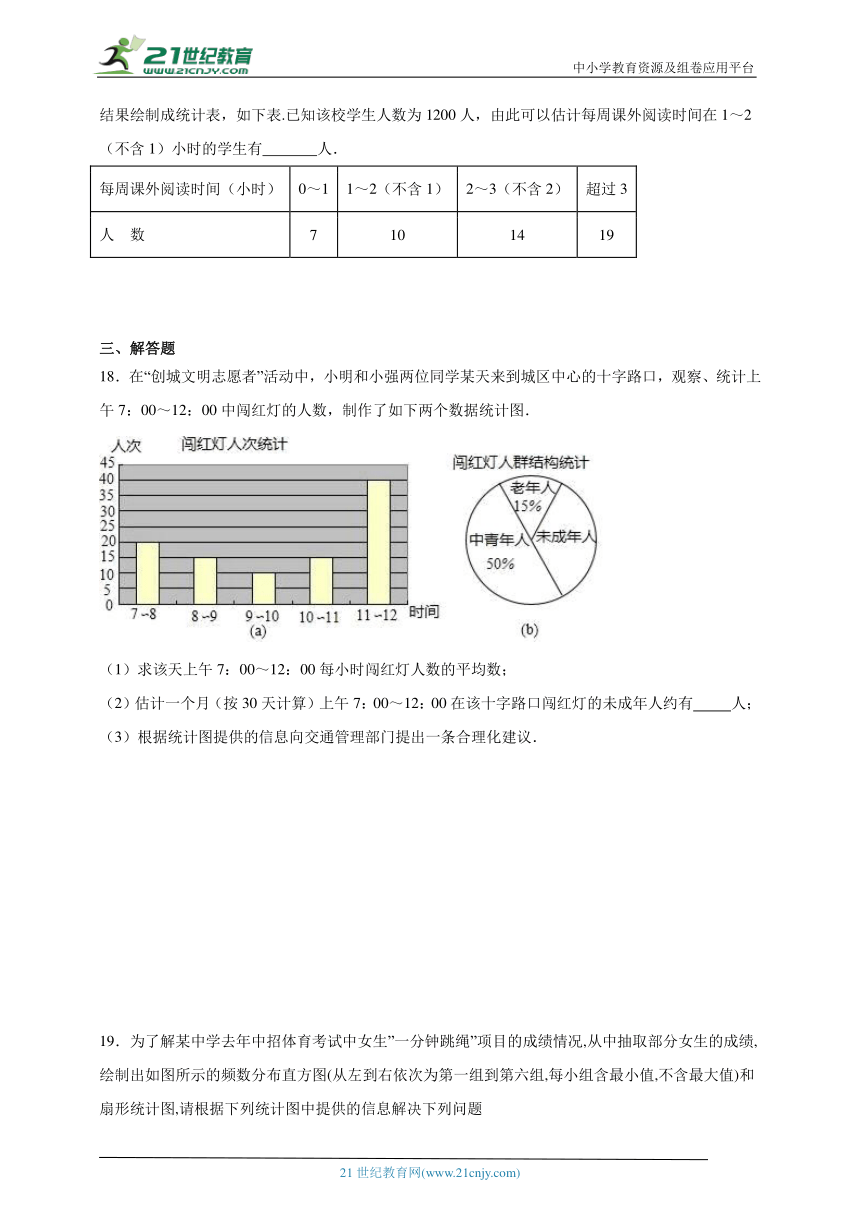
17.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表,如下表.已知该校学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有 人.
每周课外阅读时间(小时) 0~1 1~2(不含1) 2~3(不含2) 超过3
人 数 7 10 14 19
三、解答题
18.在“创城文明志愿者”活动中,小明和小强两位同学某天来到城区中心的十字路口,观察、统计上午7:00~12:00中闯红灯的人数,制作了如下两个数据统计图.
(1)求该天上午7:00~12:00每小时闯红灯人数的平均数;
(2)估计一个月(按30天计算)上午7:00~12:00在该十字路口闯红灯的未成年人约有 人;
(3)根据统计图提供的信息向交通管理部门提出一条合理化建议.
19.为了解某中学去年中招体育考试中女生”一分钟跳绳”项目的成绩情况,从中抽取部分女生的成绩,绘制出如图所示的频数分布直方图(从左到右依次为第一组到第六组,每小组含最小值,不含最大值)和扇形统计图,请根据下列统计图中提供的信息解决下列问题
(1)本次抽取的女生总人数为 第六小组人数占总人数的百分比为 请补全频数分布直方图;
(2)题中样本数据的中位数落在第 组内;
(3)若“一分钟跳绳”不低于130次的成绩为优秀,这个学校九年级共有女生560人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数.
20.在学校组织的“迎新年,做守法好公民”的知识竞赛中,每班参加比赛的人数相同,成绩分为四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将某年级的1班和2班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中,2班成绩在级以上(包括级)的人数为____人;
(2)请你将表格补充完整:
班级 平均数(分) 中位数(分) 众数(分)
1班 90
2班 87.6 100
(3)请从下列不同角度对这次竞赛成绩的结果进行分析;
①从平均数和中位数的角度来比较1班和2班的分成绩;
②从平均数和众数的角度来比较1班和2班的成绩;
③从级以上(包括级)的人数的角度来比较1班和2班的成绩.
21.某公司为了了解员工每人所创年利润情况,公司从各部门抽取部分员工对每年所创年利润情况进行统计,并绘制如图所示的统计图.
(1)求抽取员工总人数,并将图补充完整;
(2)每人所创年利润的众数是________,每人所创年利润的中位数是________,平均数是________;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?
22.在读书节活动中,某校为了解学生参加活动的情况,随机调查了部分学生每人参加活动的项数.根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为________,图①中的值为________;
(2)求统计的这组项数数据的平均数、众数和中位数.
(3)若全校有名学生,我们把参加个以上(包含个)活动的学生称为“积极学生”,则全校“积极学生”有多少人?
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B C A D A A B
题号 11 12
答案 B B
1.A
【分析】把所有数据相加可对A进行判断;利用中位数和众数的定义对B、C进行判断;利用平均数的计算公式计算出这组数据的平均,从而可对D进行判断.
【详解】A、该班级所售图书的总收入为3×14+4×11+5×10+6×15=226,所以A选项正确;
B、共50本书,第25个数为4,第26个数为5,所以这组数据的中位数为4.5,所以B选项错误;
C、这组数据的众数为6,所以C选项错误;
D、这组数据的平均数为,所以D选项错误.
故选:A.
【点睛】本题考查计算中位数,众数和平均数,熟练掌握它们的计算方法是解题的关键.
2.D
【分析】众数是一组数据中出现次数最多的数据,注意众数可以不止一个;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.
【详解】解:众数是一组数据中出现次数最多的数,在这一组数据中5.0是出现次数最多的,故众数是5.0;
而将这组数据从小到大的顺序排列后,处于中间位置的那两个数的是4.9和4.9,那么由中位数的定义可知,这组数据的中位数是4.9.
故选D.
【点睛】本题考查中位数和众数,解题的关键是熟练掌握中位数和众数的定义.
3.A
【分析】根据中位数,众数,平均数,方差等知识即可判断;
【详解】观察图象可知,共有50个学生,从低到高排列后,中位数是25位与26位的平均数,即为9.
故选A.
【点睛】本题考查中位数,众数,平均数,方差的定义,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.B
【分析】本题考查的是样本平均数和中位数的求法,掌握中位数以及平均数的求法是解题的关键.
【详解】解:将它们进行从小到大的排列为:2,3,4,4,4,4,7,
处于中间位置的数是4,
因此它们的中位数是4.
这组数据的总和为:,
而这组数据一共有7个数,
因此它们的平均数是.
故选:B.
5.C
【分析】根据众数、中位数、平均数、极差的定义和统计图中提供的数据分别列出算式,求出答案.
【详解】解:∵90出现了5次,出现的次数最多,∴众数是90;
故A正确;
∵共有10个数,∴中位数是第5、6个数的平均数,
∴中位数是(90+90)÷2=90;
故B正确;
∵平均数是(80×1+85×2+90×5+95×2)÷10=89;
故C错误;
参赛学生最高成绩与最低成绩之差是:95-80=15;
故D正确.
故选:C.
【点睛】此题考查了折线统计图,用到的知识点是众数、中位数、平均数、极差,关键是能从统计图中获得有关数据,求出众数、中位数、平均数、极差.
6.A
【分析】根据扇形统计图给出的数据,先求出销售各辆的人数,再根据平均数、中位数和众数的定义分别进行求解即可.
【详解】解:根据题意得:
销售16辆的人数是:20×40%=8(人),
销售28辆的人数是:20×15%=3(人),
销售14辆的人数是:20×20%=4(人),
销售20辆的人数是:20×25%=5(人),
则这20位销售人员本月销售量的平均数是:;
把这些数从小到大排列,最中间的数是第10、11个数,
则中位数是:,
∵销售16辆的人数最多,
∴这组数据的众数是16.
故选A.
【点睛】此题考查了平均数、中位数和众数,用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.
7.D
【分析】先根据平均数的定义求出6月份的用水量,再根据中位数和众数的定义求解可得.
【详解】解:根据题意知6月份的用水量为5×6-(3+6+4+5+6)=6(t),
∴1至6月份用水量从小到大排列为:3、4、5、6、6、6,
则该户今年1至6月份用水量的中位数为=5.5、众数为6,
故选D.
【点睛】本题主要考查众数和中位数,解题的关键是根据平均数定义求出6月份用水量及众数和中位数的定义.
8.A
【分析】在这50人中,参加6个小时体育锻炼的人数最多,则众数为6小时.
【详解】解:由条形统计图知锻炼时间为6小时的人数最多,有20人,
所以这50人一周体育锻炼时间的众数是6小时,
故选A.
【点睛】本题考查众数的意义,求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.
9.A
【详解】根据极差就是这组数中最大值与最小值的差;在一组数据中出现次数最多的数据叫众数;平均数就是把所有数据加起来再除以它们的个数.
这段时间最低气温的极差是6-1=5℃;
众数是5℃;
平均数℃.
故选A.
10.B
【分析】根据极差是数据中的最大值减去最小值,进行计算即可.
【详解】解:∵数据中最大数是,最小数是,
∴极差是.
故选:B.
11.B
【分析】A、根据众数的定义找出出现次数最多的数;B、根据中位数的定义将这组数据从小到大重新排列,求出最中间的2个数的平均数,即可得出中位数;C、根据加权平均数公式代入计算可得;D、根据方差公式计算即可.
【详解】解: A、由统计表得:众数为3,不是8,所以此选项不正确;
B、随机调查了20名学生,所以中位数是第10个和第11个学生的阅读小时数,都是3,故中位数是3,所以此选项正确;
C、平均数=,所以此选项不正确;
D、S2=×[(2﹣3.35)2+2(2.5﹣3.35)2+8(3﹣3.35)2+6(3.5﹣3.35)2+3(4﹣3.35)2]==0.2825,所以此选项不正确;
故选B.
【点睛】本题考查方差;加权平均数;中位数;众数.
12.B
【详解】解:A. 极差为:83 28=55,故错误;
B. 中位数为:(58+58)÷2=58,正确;
C. ∵58出现的次数最多,是2次,
∴众数为:58,故错误;
D.计算可知平均数为56.25大于极差.故错误.
故选B.
13. 6.8 6.5 6.5
【分析】根据条形统计图,即可知道每一名同学家庭中一年的月均用水量.再根据加权平均数的计算方法、中位数和众数的概念进行求解;
【详解】观察条形图,可知这组样本数据的平均数是: =6.8,
即这组样本数据的平均数为6.8(t).
在这组样本数据中,6.5出现了4次,出现的次数最多,
这组数据的众数是6.5(t).
将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是6.5,
有6.5+6.52=6.5,
即这组数据的中位数是6.5(t).
故答案为6.8,6.5,6.5.
【点睛】此题考查众数,中位数,加权平均数,条形统计图,解题关键在于看懂图中数据.
14.第4组
【分析】将数按从小到大顺序排列,再选取中位数即可
【详解】解:由题意可知,共50个数据,中位数为第25和第26个数的平均数,
所以这个样本的中位数在第4组.
故答案为第4组.
【点睛】本题考查中位数定义,基础知识扎实是本题解题关键
15.8
【详解】依题意得:a=5×5-3-6-4-2=10,
方差S2=[(3-5)2+(6-5)2+(10-5)2+(4-5)2+(2-5)2]=×40=8.
16.先生产丙产品,再生产乙产品,最后生产甲产品
【分析】按“相对等待时间”为该笔订单的等待时间与生产线完成该订单所需时间之比,要想“相对等待时间”之和最小,则生产线需要将生产时间最长的产品排在最后生产,生产时间最短的产品排在最前生产,这样订单的等待时间最短即可求解.
【详解】解:按按“相对等待时间”为该笔订单的等待时间与生产线完成该订单所需时间之比,要想“相对等待时间”之和最小,则生产线需要将生产时间最长的产品排在最后生产,生产时间最短的产品排在最前生产,这样订单的等待时间最短,
由题意可知:甲、乙、丙三笔订单的生产时间从短到长为排列为:丙、乙、甲,
∴优先生产丙产品,其次生产乙产品,最后生产甲产品,此时三笔订单“相对等待时间”之和最小,
故答案为:先生产丙产品,再生产乙产品,最后生产甲产品.
【点睛】本题属于新定义题型,按照题意中的方法或要求来解题,读懂题意,明确题意中的“相对等待时间”这个概念是解决本类题的关键.
17.240
【详解】试题分析:先求出每周课外阅读时间在1~2(不含1)小时的学生所占的百分比,再乘以全校的人数,即可得出答案.
解:根据题意得:
1200×=240(人),
答:估计每周课外阅读时间在1~2(不含1)小时的学生有240人;
故答案为240.
考点:用样本估计总体.
18.(1)20(人);(2)1050;(3)加强对11~12点时段的交通管理和交通安全教育.
【分析】(1)用闯红灯的总人数除以时间,即可解答
(2)题目意思是要用样本估计总体,那先要知道天闯红灯的未成年人占总人数的百分比和总人数,用样本的百分比估计总体的百分比,根据部分数量=总体数量x百分比x天数,即可;
(3)根据题目意思,结合两个统计图和计算的数据,只要说的合理就行
【详解】解:(1)该天上午7:00~12:00每小时闯红灯人数的平均数是:(20+15+10+15+40)÷5=20(人);
(2)30×(20×5)×(1﹣50%﹣15%)=1050(人).
故答案为1050;
(3)加强对11~12点时段的交通管理和交通安全教育.
【点睛】此题考查加权平均数,算术平均数,条形统计图,扇形统计图,解题关键在于看懂图中数据
19.(1)50,8%,频数分布直方图补充见解析;(2)三;(3)估计该校九年级女生“一分钟跳绳”成绩优秀的人数为224人
【分析】(1)根据第二小组的人数以及百分比求出总体个数,再求出第四小组人数 即可解决问题.
(2)根据中位数的定义即可解决问题.
(3)用样本估计总体的思想即可解决问题.
【详解】解:(1)由两幅统计图中的信息可得:被抽查总数为:10÷20%=50(人),
∴第六组人数占总数人数的百分比为:4÷50×100%=8%,
第四组的人数为:50-4-10-16-6-4=10,
频数分布直方图补充如下
故答案是:50人、8%;
(2) 因为总人数为50,
所以中位数是第25、26个数据的平均数,
而第25、26个数据都落在第三组,
所以中位数落在第三组,
故答案为三;
(3)随机抽取的样本中,不低于130次的有20人,
则总体560人中优秀的有×560=224(人)
答:估计该校九年级女生“一分钟跳绳”成绩优秀的人数为224人
20.(1)21(2)见解析(3)①一班成绩好②二班成绩好③一班成绩好
【分析】(1)用总人数×二班成绩在C级以上(包括C级)的人数所占百分比即可;
(2)从扇形统计图中的数据求出各个等级的人数,按找中位数和众数的方法得出中位数和众数;
(3)根据(1)(2)的计算结果分析比较.
【详解】(1)根据统计图可得:
级所占的百分比是:
总人数是:
竞赛中二班成绩在级以上(包括级)的人数为
(人)
(2)根据图形可得:
一班数据90出现12次,出现次数最多,所以众数为90
二班100分的有人
90分的有人
80分的有人
70分的有人
按从小到大顺序排殒,中位数为80
班级 平均数(分) 中位数(分) 众数(分)
1班 87.6 90 90
2班 87.6 80 100
(3)①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班成绩好
②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好
③从级以上(包括级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班成绩好
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.除此之外,本题也考查了对平均数、中位数、众数的认识.
21.(1)见解析(2)8万元,8万元,8.12万元(3)384人
【分析】试题分析:(1)根据扇形中各部分所占的百分比的和是1,即可求得3万元的员工所占的百分比,然后根据百分比的意义求得直方图中缺少部分的人数;
(2)根据众数、中位数以及平均数的定义求解;
(3)利用总数1200乘以对应的比例即可求解.
【详解】试题解析:(1)3万元的员工的百分比为:1﹣36%﹣20%﹣12%﹣24%=8%,
抽取员工总数为:4÷8%=50(人)
5万元的员工人数为:50×24%=12(人)
8万元的员工人数为:50×36%=18(人)
(2)每人所创年利润的众数是 8万元,每人所创年利润的中位数是8万元,
平均数是:(3×4+5×12+8×18+10×10+15×6)=8.12万元.
故答案为8万元,8万元,8.12万元.
(3)1200×=384(人).
答:在公司1200员工中有384人可以评为优秀员工.
【点睛】考点: 条形统计图;用样本估计总体;扇形统计图;加权平均数;中位数.
22.(1);
(2)平均数是,众数是,中位数是
(3)人
【分析】本题考查数据的收集、处理、分析和统计,解题的关键是掌握平均数,众数,中位数的定义,即可.
(1)根据条形统计图和扇形统计图,即可求出总人数;
(2)根据平均数,众数,中位数的定义,即可;
(3)根据样本估计总体,即可.
【详解】(1)由题意得,参加两项的学生人数是人,占总人数的,
∴总人数为:(人);
∵参加项的学生人数是人,
∴占比为:;
故答案为:;.
(2)平均数为:;
∵在这组数据中,出现了次,出现了次,出现了次,出现了次,
∴众数为:;
∵将该组数据按从小到大的顺序排列,其中处于中间的两个数为,
∴,
∴中位数为:.
(3)∵参加个以上(包含个)活动的“积极学生”有人,
∴全校有名学生中,全校“积极学生”为(人).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
20.3课题学习体质健康测试中的数据分析
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.学校举行图书节义卖活动,将所售款项捐给其他贫困学生,在这次义卖活动中,某班级售书情况如下表:
售价 元 元 元 元
数目 本 本 本 本
下列说法正确的是( )
A.该班级所售图书的总收入是元 B.在该班级所传图书价格组成的一组数据中,中位数是元
C.在该班级所售图书价格组成的一组数据中,众数是元 D.在该班级所售图书价格组成的一组数据中,平均数是元
2.某班40名学生右眼视力的检查结果如下表所示:
视力 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2
人数 1 2 3 2 3 4 4 6 10 4 1
这组数据的众数和中位数分别是( )
A.5.0,4.7 B.4.9,4.9 C.4.9,4.7 D.5.0,4.9
3.在刚刚结束的中考英语听力、口语测试中,某班口语成绩情况如图所示,则下列说法正确的是( )
A.中位数是9 B.众数为16 C.平均分为7.78 D.方差为2
4.下表是食品营养成分表的一部分(每100克食品中可食部分营养成分的含量)
蔬菜种类 绿豆芽 白 菜 油 菜 卷心菜 菠 菜 韭 菜 胡萝卜(红)
碳水化合物(克) 4 3 4 4 2 4 7
在表中提供的碳水化合物的克数所组成的数据中,中位数,平均数是( )
A.3 ;5 B.4 ;4 C.2 ;3 D.3;7
5.某校10名学生参加某项比赛成绩统计如图所示。对于这10名学生的参赛成绩,下列说法中错误的是( )
A.众数是90 B.中位数是90
C.平均数是90 D.参赛学生最高成绩与最低成绩之差是15
6.某品牌汽车公司销售部为了制定下个月的销售计划,对 20 位销售员本月的销售量进行了 统计,绘制成如图所示的统计图,则这 20 位销售人员本月销售量的平均数、中位数、众数 分别是(单位:辆)( )
A.18.4,16,16 B.18.4,20,16
C.19, 16,16 D.19, 20,16
7.某居民今年1至6月份(共6个月)的月平均用水量5t,其中1至5月份月用水量(单位:t)统计如图所示,根据表中信息,该户今年1至6月份用水量的中位数和众数分别是( )
A.4,5 B.4.5,6 C.5,6 D.5.5,6
8.为了了解阳光居民小区“全民健身”活动的开展情况,某志愿者随机调查了该小区50名成年居民一周的体育锻炼时间,并将数据进行整理后绘制成如图所示的统计图,则这50人一周体育锻炼时间的众数是( )
A.6小时 B.20人 C.10小时 D.3人
9.如图是根据某地4月上旬每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是( ).
A.5° 5° 4° B.5° 5° 4.5° C.2.8° 5° 4° D.2.8° 5° 4.5°
10.一组学生的身高是(单位:米),则这组学生身高数据的极差是( )
A.2 B. C. D.0
11.李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间(小时) 2 2.5 3 3.5 4
学生人数(名) 1 2 8 6 3
则关于这20名学生阅读小时数的说法正确的是( )
A.众数是8 B.中位数是3
C.平均数是3 D.方差是0.34
12.某学校七年级1班统计了全班同学在1~8月份的课外阅读数量(单位:本),绘制了右边的折线统计图,下列说法正确的是( )
A.极差是47 B.中位数是58 C.众数是42 D.极差大于平均数
二、填空题
13.我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图,则这10个样本数据的平均数是 ,众数是 ,中位数是 .
14.某校901班共有50名同学,如图是该次体育模拟测试成绩的频数分布直方图(满分为30分,成绩均为整数),则测试成绩的中位数所在的组别是 .
15.样本数据3,6,a,4,2的平均数是5,则这个样本的方差是
16.某生产线在同一时间只能生产一笔订单,即在完成一笔订单后才能开始生产下一笔订单中的产品.一笔订单的“相对等待时间”定义为该笔订单的等待时间与生产线完成该订单所需时间之比.例如,该生产线完成第一笔订单用时5小时,之后完成第二笔订单用时2小时,则第一笔订单的“相对等待时间”为0,第二笔订单的“相对等待时间”为.现有甲、乙、丙三笔订单管理员估测这三笔订单的生产时间(单位:小时)依次为a,b,c,其中,则使三笔订单“相对等待时间”之和最小的生产顺序是 .
17.某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表,如下表.已知该校学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有 人.
每周课外阅读时间(小时) 0~1 1~2(不含1) 2~3(不含2) 超过3
人 数 7 10 14 19
三、解答题
18.在“创城文明志愿者”活动中,小明和小强两位同学某天来到城区中心的十字路口,观察、统计上午7:00~12:00中闯红灯的人数,制作了如下两个数据统计图.
(1)求该天上午7:00~12:00每小时闯红灯人数的平均数;
(2)估计一个月(按30天计算)上午7:00~12:00在该十字路口闯红灯的未成年人约有 人;
(3)根据统计图提供的信息向交通管理部门提出一条合理化建议.
19.为了解某中学去年中招体育考试中女生”一分钟跳绳”项目的成绩情况,从中抽取部分女生的成绩,绘制出如图所示的频数分布直方图(从左到右依次为第一组到第六组,每小组含最小值,不含最大值)和扇形统计图,请根据下列统计图中提供的信息解决下列问题
(1)本次抽取的女生总人数为 第六小组人数占总人数的百分比为 请补全频数分布直方图;
(2)题中样本数据的中位数落在第 组内;
(3)若“一分钟跳绳”不低于130次的成绩为优秀,这个学校九年级共有女生560人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数.
20.在学校组织的“迎新年,做守法好公民”的知识竞赛中,每班参加比赛的人数相同,成绩分为四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将某年级的1班和2班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中,2班成绩在级以上(包括级)的人数为____人;
(2)请你将表格补充完整:
班级 平均数(分) 中位数(分) 众数(分)
1班 90
2班 87.6 100
(3)请从下列不同角度对这次竞赛成绩的结果进行分析;
①从平均数和中位数的角度来比较1班和2班的分成绩;
②从平均数和众数的角度来比较1班和2班的成绩;
③从级以上(包括级)的人数的角度来比较1班和2班的成绩.
21.某公司为了了解员工每人所创年利润情况,公司从各部门抽取部分员工对每年所创年利润情况进行统计,并绘制如图所示的统计图.
(1)求抽取员工总人数,并将图补充完整;
(2)每人所创年利润的众数是________,每人所创年利润的中位数是________,平均数是________;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?
22.在读书节活动中,某校为了解学生参加活动的情况,随机调查了部分学生每人参加活动的项数.根据统计的结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(1)本次接受调查的学生人数为________,图①中的值为________;
(2)求统计的这组项数数据的平均数、众数和中位数.
(3)若全校有名学生,我们把参加个以上(包含个)活动的学生称为“积极学生”,则全校“积极学生”有多少人?
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A D A B C A D A A B
题号 11 12
答案 B B
1.A
【分析】把所有数据相加可对A进行判断;利用中位数和众数的定义对B、C进行判断;利用平均数的计算公式计算出这组数据的平均,从而可对D进行判断.
【详解】A、该班级所售图书的总收入为3×14+4×11+5×10+6×15=226,所以A选项正确;
B、共50本书,第25个数为4,第26个数为5,所以这组数据的中位数为4.5,所以B选项错误;
C、这组数据的众数为6,所以C选项错误;
D、这组数据的平均数为,所以D选项错误.
故选:A.
【点睛】本题考查计算中位数,众数和平均数,熟练掌握它们的计算方法是解题的关键.
2.D
【分析】众数是一组数据中出现次数最多的数据,注意众数可以不止一个;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数.
【详解】解:众数是一组数据中出现次数最多的数,在这一组数据中5.0是出现次数最多的,故众数是5.0;
而将这组数据从小到大的顺序排列后,处于中间位置的那两个数的是4.9和4.9,那么由中位数的定义可知,这组数据的中位数是4.9.
故选D.
【点睛】本题考查中位数和众数,解题的关键是熟练掌握中位数和众数的定义.
3.A
【分析】根据中位数,众数,平均数,方差等知识即可判断;
【详解】观察图象可知,共有50个学生,从低到高排列后,中位数是25位与26位的平均数,即为9.
故选A.
【点睛】本题考查中位数,众数,平均数,方差的定义,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.B
【分析】本题考查的是样本平均数和中位数的求法,掌握中位数以及平均数的求法是解题的关键.
【详解】解:将它们进行从小到大的排列为:2,3,4,4,4,4,7,
处于中间位置的数是4,
因此它们的中位数是4.
这组数据的总和为:,
而这组数据一共有7个数,
因此它们的平均数是.
故选:B.
5.C
【分析】根据众数、中位数、平均数、极差的定义和统计图中提供的数据分别列出算式,求出答案.
【详解】解:∵90出现了5次,出现的次数最多,∴众数是90;
故A正确;
∵共有10个数,∴中位数是第5、6个数的平均数,
∴中位数是(90+90)÷2=90;
故B正确;
∵平均数是(80×1+85×2+90×5+95×2)÷10=89;
故C错误;
参赛学生最高成绩与最低成绩之差是:95-80=15;
故D正确.
故选:C.
【点睛】此题考查了折线统计图,用到的知识点是众数、中位数、平均数、极差,关键是能从统计图中获得有关数据,求出众数、中位数、平均数、极差.
6.A
【分析】根据扇形统计图给出的数据,先求出销售各辆的人数,再根据平均数、中位数和众数的定义分别进行求解即可.
【详解】解:根据题意得:
销售16辆的人数是:20×40%=8(人),
销售28辆的人数是:20×15%=3(人),
销售14辆的人数是:20×20%=4(人),
销售20辆的人数是:20×25%=5(人),
则这20位销售人员本月销售量的平均数是:;
把这些数从小到大排列,最中间的数是第10、11个数,
则中位数是:,
∵销售16辆的人数最多,
∴这组数据的众数是16.
故选A.
【点睛】此题考查了平均数、中位数和众数,用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.
7.D
【分析】先根据平均数的定义求出6月份的用水量,再根据中位数和众数的定义求解可得.
【详解】解:根据题意知6月份的用水量为5×6-(3+6+4+5+6)=6(t),
∴1至6月份用水量从小到大排列为:3、4、5、6、6、6,
则该户今年1至6月份用水量的中位数为=5.5、众数为6,
故选D.
【点睛】本题主要考查众数和中位数,解题的关键是根据平均数定义求出6月份用水量及众数和中位数的定义.
8.A
【分析】在这50人中,参加6个小时体育锻炼的人数最多,则众数为6小时.
【详解】解:由条形统计图知锻炼时间为6小时的人数最多,有20人,
所以这50人一周体育锻炼时间的众数是6小时,
故选A.
【点睛】本题考查众数的意义,求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据.
9.A
【详解】根据极差就是这组数中最大值与最小值的差;在一组数据中出现次数最多的数据叫众数;平均数就是把所有数据加起来再除以它们的个数.
这段时间最低气温的极差是6-1=5℃;
众数是5℃;
平均数℃.
故选A.
10.B
【分析】根据极差是数据中的最大值减去最小值,进行计算即可.
【详解】解:∵数据中最大数是,最小数是,
∴极差是.
故选:B.
11.B
【分析】A、根据众数的定义找出出现次数最多的数;B、根据中位数的定义将这组数据从小到大重新排列,求出最中间的2个数的平均数,即可得出中位数;C、根据加权平均数公式代入计算可得;D、根据方差公式计算即可.
【详解】解: A、由统计表得:众数为3,不是8,所以此选项不正确;
B、随机调查了20名学生,所以中位数是第10个和第11个学生的阅读小时数,都是3,故中位数是3,所以此选项正确;
C、平均数=,所以此选项不正确;
D、S2=×[(2﹣3.35)2+2(2.5﹣3.35)2+8(3﹣3.35)2+6(3.5﹣3.35)2+3(4﹣3.35)2]==0.2825,所以此选项不正确;
故选B.
【点睛】本题考查方差;加权平均数;中位数;众数.
12.B
【详解】解:A. 极差为:83 28=55,故错误;
B. 中位数为:(58+58)÷2=58,正确;
C. ∵58出现的次数最多,是2次,
∴众数为:58,故错误;
D.计算可知平均数为56.25大于极差.故错误.
故选B.
13. 6.8 6.5 6.5
【分析】根据条形统计图,即可知道每一名同学家庭中一年的月均用水量.再根据加权平均数的计算方法、中位数和众数的概念进行求解;
【详解】观察条形图,可知这组样本数据的平均数是: =6.8,
即这组样本数据的平均数为6.8(t).
在这组样本数据中,6.5出现了4次,出现的次数最多,
这组数据的众数是6.5(t).
将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是6.5,
有6.5+6.52=6.5,
即这组数据的中位数是6.5(t).
故答案为6.8,6.5,6.5.
【点睛】此题考查众数,中位数,加权平均数,条形统计图,解题关键在于看懂图中数据.
14.第4组
【分析】将数按从小到大顺序排列,再选取中位数即可
【详解】解:由题意可知,共50个数据,中位数为第25和第26个数的平均数,
所以这个样本的中位数在第4组.
故答案为第4组.
【点睛】本题考查中位数定义,基础知识扎实是本题解题关键
15.8
【详解】依题意得:a=5×5-3-6-4-2=10,
方差S2=[(3-5)2+(6-5)2+(10-5)2+(4-5)2+(2-5)2]=×40=8.
16.先生产丙产品,再生产乙产品,最后生产甲产品
【分析】按“相对等待时间”为该笔订单的等待时间与生产线完成该订单所需时间之比,要想“相对等待时间”之和最小,则生产线需要将生产时间最长的产品排在最后生产,生产时间最短的产品排在最前生产,这样订单的等待时间最短即可求解.
【详解】解:按按“相对等待时间”为该笔订单的等待时间与生产线完成该订单所需时间之比,要想“相对等待时间”之和最小,则生产线需要将生产时间最长的产品排在最后生产,生产时间最短的产品排在最前生产,这样订单的等待时间最短,
由题意可知:甲、乙、丙三笔订单的生产时间从短到长为排列为:丙、乙、甲,
∴优先生产丙产品,其次生产乙产品,最后生产甲产品,此时三笔订单“相对等待时间”之和最小,
故答案为:先生产丙产品,再生产乙产品,最后生产甲产品.
【点睛】本题属于新定义题型,按照题意中的方法或要求来解题,读懂题意,明确题意中的“相对等待时间”这个概念是解决本类题的关键.
17.240
【详解】试题分析:先求出每周课外阅读时间在1~2(不含1)小时的学生所占的百分比,再乘以全校的人数,即可得出答案.
解:根据题意得:
1200×=240(人),
答:估计每周课外阅读时间在1~2(不含1)小时的学生有240人;
故答案为240.
考点:用样本估计总体.
18.(1)20(人);(2)1050;(3)加强对11~12点时段的交通管理和交通安全教育.
【分析】(1)用闯红灯的总人数除以时间,即可解答
(2)题目意思是要用样本估计总体,那先要知道天闯红灯的未成年人占总人数的百分比和总人数,用样本的百分比估计总体的百分比,根据部分数量=总体数量x百分比x天数,即可;
(3)根据题目意思,结合两个统计图和计算的数据,只要说的合理就行
【详解】解:(1)该天上午7:00~12:00每小时闯红灯人数的平均数是:(20+15+10+15+40)÷5=20(人);
(2)30×(20×5)×(1﹣50%﹣15%)=1050(人).
故答案为1050;
(3)加强对11~12点时段的交通管理和交通安全教育.
【点睛】此题考查加权平均数,算术平均数,条形统计图,扇形统计图,解题关键在于看懂图中数据
19.(1)50,8%,频数分布直方图补充见解析;(2)三;(3)估计该校九年级女生“一分钟跳绳”成绩优秀的人数为224人
【分析】(1)根据第二小组的人数以及百分比求出总体个数,再求出第四小组人数 即可解决问题.
(2)根据中位数的定义即可解决问题.
(3)用样本估计总体的思想即可解决问题.
【详解】解:(1)由两幅统计图中的信息可得:被抽查总数为:10÷20%=50(人),
∴第六组人数占总数人数的百分比为:4÷50×100%=8%,
第四组的人数为:50-4-10-16-6-4=10,
频数分布直方图补充如下
故答案是:50人、8%;
(2) 因为总人数为50,
所以中位数是第25、26个数据的平均数,
而第25、26个数据都落在第三组,
所以中位数落在第三组,
故答案为三;
(3)随机抽取的样本中,不低于130次的有20人,
则总体560人中优秀的有×560=224(人)
答:估计该校九年级女生“一分钟跳绳”成绩优秀的人数为224人
20.(1)21(2)见解析(3)①一班成绩好②二班成绩好③一班成绩好
【分析】(1)用总人数×二班成绩在C级以上(包括C级)的人数所占百分比即可;
(2)从扇形统计图中的数据求出各个等级的人数,按找中位数和众数的方法得出中位数和众数;
(3)根据(1)(2)的计算结果分析比较.
【详解】(1)根据统计图可得:
级所占的百分比是:
总人数是:
竞赛中二班成绩在级以上(包括级)的人数为
(人)
(2)根据图形可得:
一班数据90出现12次,出现次数最多,所以众数为90
二班100分的有人
90分的有人
80分的有人
70分的有人
按从小到大顺序排殒,中位数为80
班级 平均数(分) 中位数(分) 众数(分)
1班 87.6 90 90
2班 87.6 80 100
(3)①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班成绩好
②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好
③从级以上(包括级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班成绩好
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.除此之外,本题也考查了对平均数、中位数、众数的认识.
21.(1)见解析(2)8万元,8万元,8.12万元(3)384人
【分析】试题分析:(1)根据扇形中各部分所占的百分比的和是1,即可求得3万元的员工所占的百分比,然后根据百分比的意义求得直方图中缺少部分的人数;
(2)根据众数、中位数以及平均数的定义求解;
(3)利用总数1200乘以对应的比例即可求解.
【详解】试题解析:(1)3万元的员工的百分比为:1﹣36%﹣20%﹣12%﹣24%=8%,
抽取员工总数为:4÷8%=50(人)
5万元的员工人数为:50×24%=12(人)
8万元的员工人数为:50×36%=18(人)
(2)每人所创年利润的众数是 8万元,每人所创年利润的中位数是8万元,
平均数是:(3×4+5×12+8×18+10×10+15×6)=8.12万元.
故答案为8万元,8万元,8.12万元.
(3)1200×=384(人).
答:在公司1200员工中有384人可以评为优秀员工.
【点睛】考点: 条形统计图;用样本估计总体;扇形统计图;加权平均数;中位数.
22.(1);
(2)平均数是,众数是,中位数是
(3)人
【分析】本题考查数据的收集、处理、分析和统计,解题的关键是掌握平均数,众数,中位数的定义,即可.
(1)根据条形统计图和扇形统计图,即可求出总人数;
(2)根据平均数,众数,中位数的定义,即可;
(3)根据样本估计总体,即可.
【详解】(1)由题意得,参加两项的学生人数是人,占总人数的,
∴总人数为:(人);
∵参加项的学生人数是人,
∴占比为:;
故答案为:;.
(2)平均数为:;
∵在这组数据中,出现了次,出现了次,出现了次,出现了次,
∴众数为:;
∵将该组数据按从小到大的顺序排列,其中处于中间的两个数为,
∴,
∴中位数为:.
(3)∵参加个以上(包含个)活动的“积极学生”有人,
∴全校有名学生中,全校“积极学生”为(人).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
