29.1投影同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
29.1投影
学校:___________姓名:___________班级:___________考号:___________
一、单选题
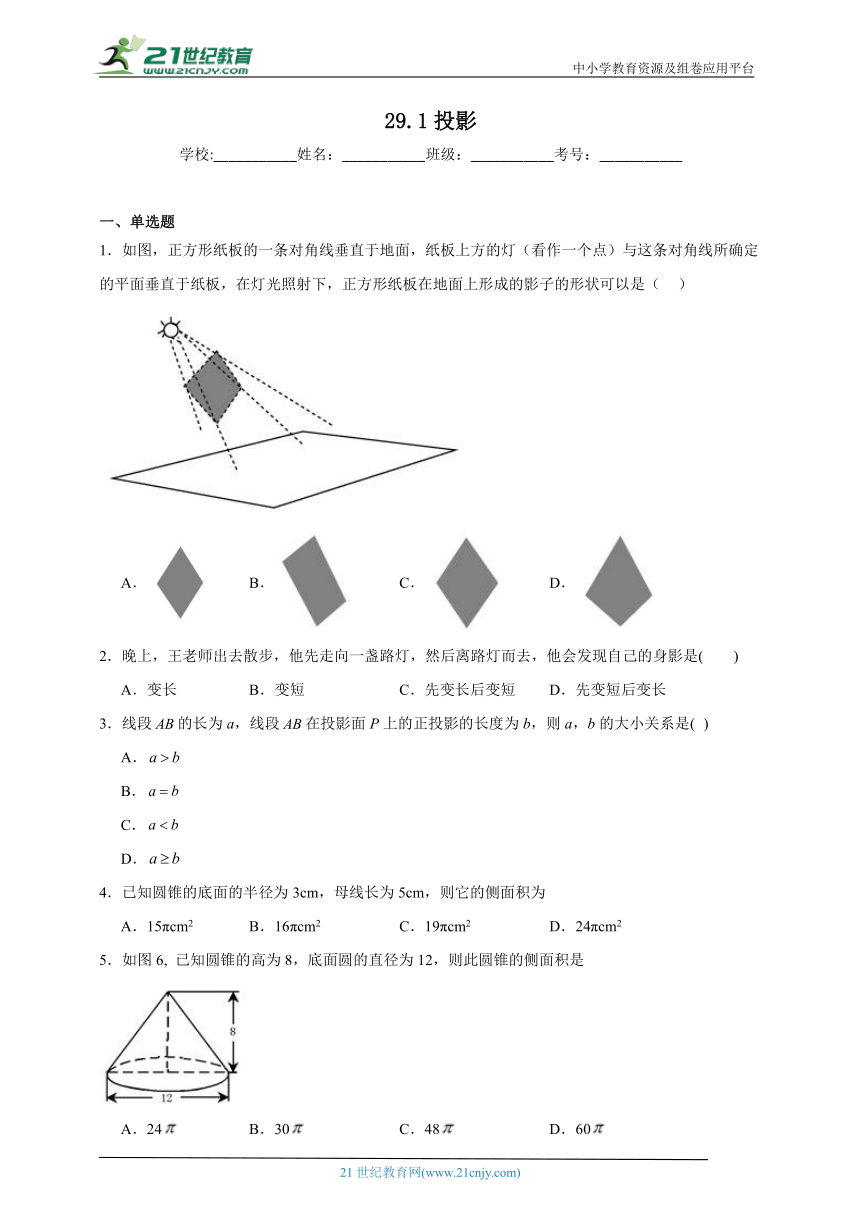
1.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
2.晚上,王老师出去散步,他先走向一盏路灯,然后离路灯而去,他会发现自己的身影是( )
A.变长 B.变短 C.先变长后变短 D.先变短后变长
3.线段的长为a,线段在投影面P上的正投影的长度为b,则a,b的大小关系是( )
A.
B.
C.
D.
4.已知圆锥的底面的半径为3cm,母线长为5cm,则它的侧面积为
A.15πcm2 B.16πcm2 C.19πcm2 D.24πcm2
5.如图6, 已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是
A.24 B.30 C.48 D.60
6.下列哪种光线形成的投影是平行投影( )
A.太阳 B.探照灯 C.手电筒 D.路灯
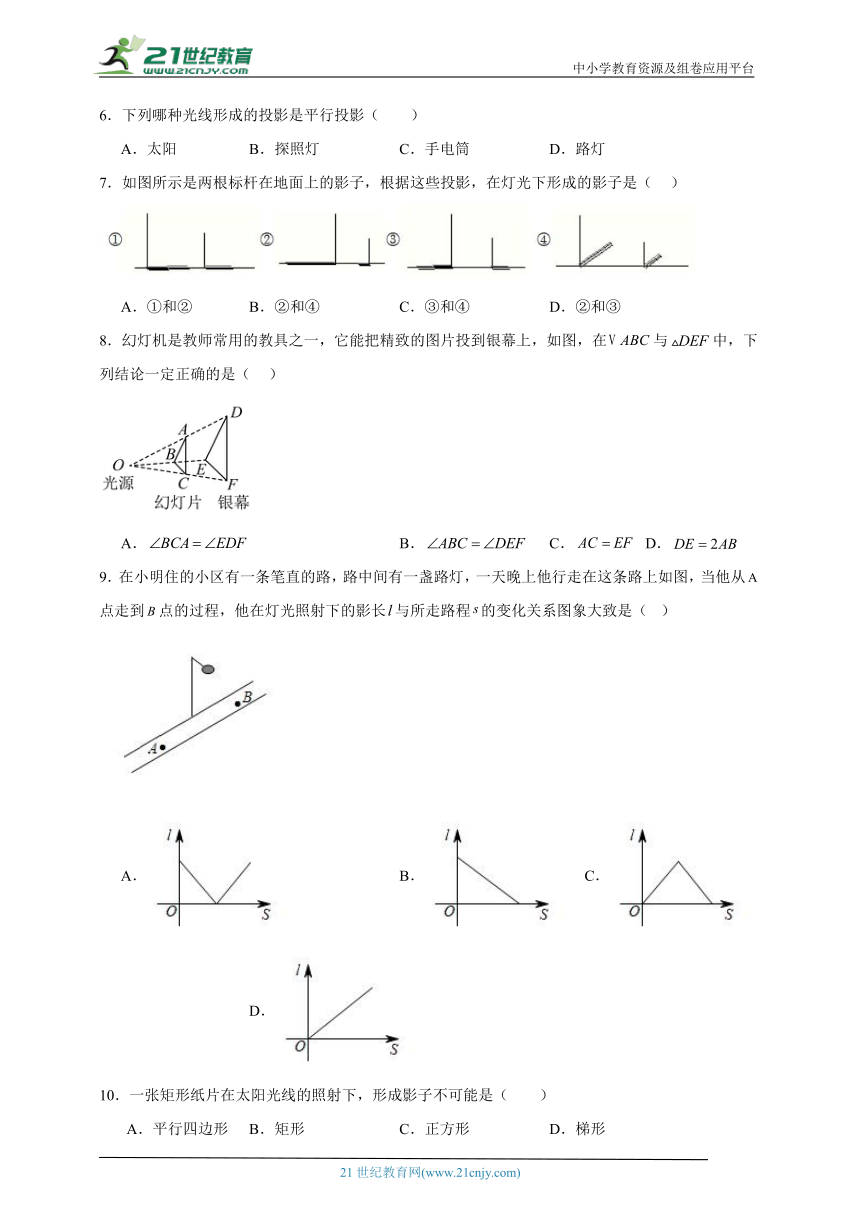
7.如图所示是两根标杆在地面上的影子,根据这些投影,在灯光下形成的影子是( )
A.①和② B.②和④ C.③和④ D.②和③
8.幻灯机是教师常用的教具之一,它能把精致的图片投到银幕上,如图,在与中,下列结论一定正确的是( )
A. B. C. D.
9.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上他行走在这条路上如图,当他从点走到点的过程,他在灯光照射下的影长与所走路程的变化关系图象大致是( )
A. B. C. D.
10.一张矩形纸片在太阳光线的照射下,形成影子不可能是( )
A.平行四边形 B.矩形 C.正方形 D.梯形
11.张强的身高和李华的身高一样,那么在同一路灯下( )
A.小明的影子比小强的影子长 B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
12.一个正五棱柱如下图摆放,光线由上到下照射此正五棱柱时的正投影是( )
A. B. C. D.
二、填空题
13.大型礼堂中的座位都呈阶梯状安放,这样安放的道理是 .
14.如图,同一时刻小诚和大树的影子长分别为和,已知小诚身高,则大树的高度为 m.
15.路灯下行人的影子属于 投影.(填“平行”或“中心”)
16.小明家的客厅有一张直径为1米,高0.75米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中点D的坐标为,则点E的坐标是 .
17.一般地,用光线照射物体,在某个平面 (地面、墙壁等) 上得到的影子叫做物体的 .照射光线叫做 ,投影所在的平面叫做 .
三、解答题
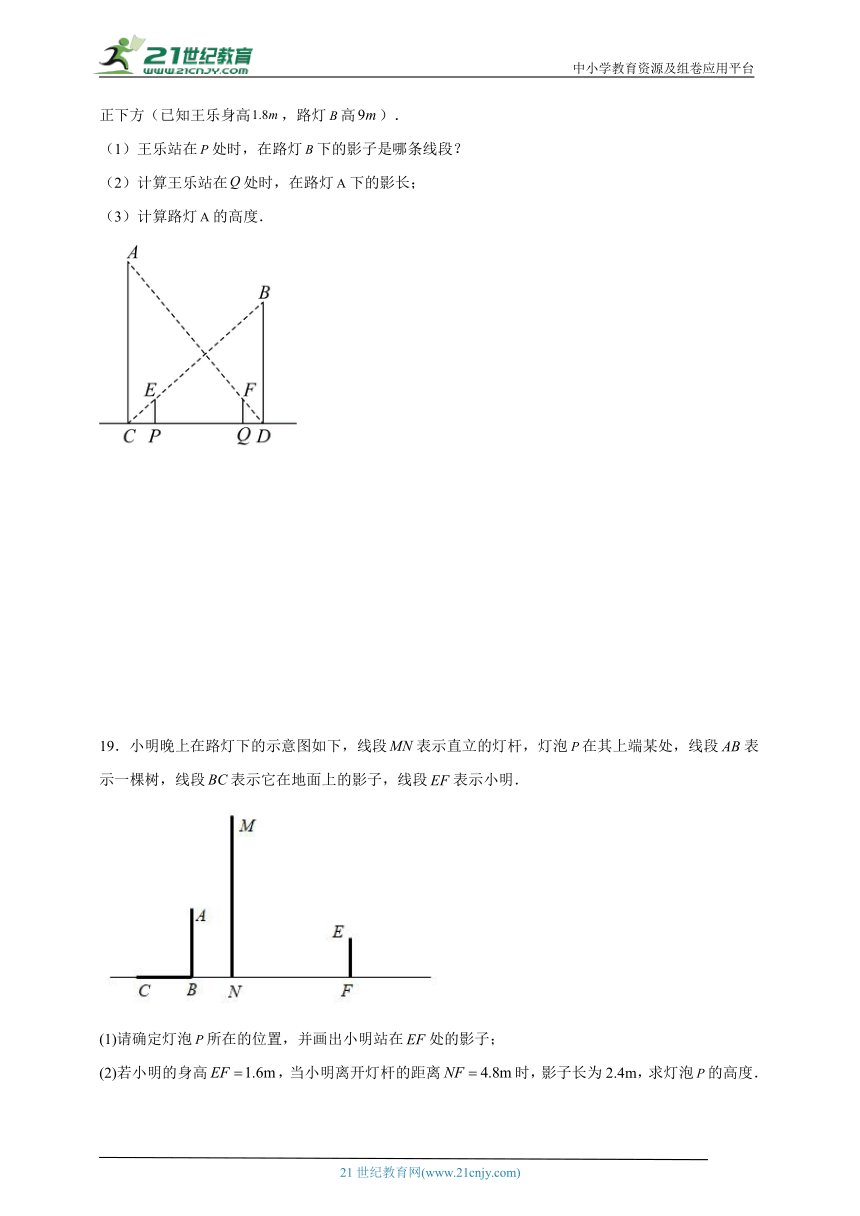
18.如图,王乐同学在晩上由路灯走向路灯.当他行到处时发现,他往路灯下的影长为2m,且恰好位于路灯的正下方,接着他又走了到处,此时他在路灯下的影子恰好位于路灯的正下方(已知王乐身高,路灯高).
(1)王乐站在处时,在路灯下的影子是哪条线段?
(2)计算王乐站在处时,在路灯下的影长;
(3)计算路灯的高度.
19.小明晚上在路灯下的示意图如下,线段表示直立的灯杆,灯泡在其上端某处,线段表示一棵树,线段表示它在地面上的影子,线段表示小明.
(1)请确定灯泡所在的位置,并画出小明站在处的影子;
(2)若小明的身高,当小明离开灯杆的距离时,影子长为2.4m,求灯泡的高度.
20.小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.数学活动小组的同学对该塔进行了测量,测量方法如下:如图,小铭在小雁塔的影子顶端处竖直立一根木棒,并测得此时木棒的影长;然后,小希在的延长线上找出一点,使得、、三点在同一直线上,并测得.已知图中所有点均在同一平面内,木棒,,,请根据以上测量数据,求小雁塔的高度.
21.如图,是小亮晚上散步回家的场景,图中线段表示站立在路灯左侧的小亮,线段表示直立在地面上的路灯,点P表示照明灯的位置.当小亮与路灯之间的距离时,其身后的影长为,已知小亮的身高为,当小亮步行至路灯右侧且距路灯的点D处时,小亮身前的影长是多少米?(结果用分数表示)
22.如图,亮亮、明明利用家门口路灯的灯光来测量该路灯的高度,明明在A处时,亮亮测得明明的影长为2米,明明向前走2米到B处时,亮亮测得明明的影长为1米,已知明明的身高,为米,
(1)求路灯高
(2)在此路灯下,明明在直线上运动,明明应由点A前进或后退多少米,亮亮恰好测得明明的影长是其身高的2倍.
23.操作与研究:如图,被平行于的光线照射,于D,在投影面上.
(1)指出图中线段的投影是______,线段的投影是______.
(2)问题情景:如图1,中,,,我们可以利用与相似证明,这个结论我们称之为射影定理,请证明这个定理.
(3)拓展运用:如图2,正方形的边长为15,点O是对角线、的交点,点E在上,过点C作,垂足为F,连接;试利用射影定理证明;
24.操作与研究∶如图,被平行于的光线照射,于,在投影面上.
(1)指出图中的投影是什么,与的投影呢?
(2)探究∶ 如图1,中,,,我们可以利用与相似证明, 这个结论我们称之为射影定理,试证明这个定理.
(3)【结论运用】如图2,正方形的边长为,点是对角线的交点,点在上,过点作,垂足为,连接,
①试利用射影定理证明;
②若,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D A D A D B A D
题号 11 12
答案 D B
1.D
【分析】因为中心投影物体的高和影长成比例,正确的区分中心投影和平行投影,依次分析选项即可找到符合题意的选项
【详解】因为正方形的对角线互相垂直,且一条对角线垂直地面,光源与对角线组成的平面垂直于地面,则有影子的对角线仍然互相垂直,且由于光源在平板的上方,则上方的边长影子会更长一些,
故选D
【点睛】本题考查了中心投影的概念,应用,利用中心投影的特点,理解中心投影物体的高和影长成比例是解题的关键.
2.D
【分析】由题意可得王老师离光源是由远到近再到远的过程,根据中心投影的特点,即可得到身影的变化特点.
【详解】王老师经过一盏路灯的过程中,王老师离光源是由远到近再到远的过程,所以他在地上的影子先变短后变长.
故选D.
【点睛】本题考查了中心投影的特点和规律.中心投影的特点是:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
3.D
【分析】本题考查了平行投影,分三种情况考虑即可;
【详解】当线段平行于投影面放置时,;当线段倾斜于投影面放置时,;当线段垂直于投影面放置时,.
综上知,.
故选D
4.A
【详解】试题分析:S==15π.
考点:圆锥的侧面积计算.
5.D
【详解】由图可知,圆锥半径为6,高为8,∴母线长为10,∴圆锥的侧面积是=
==,故选D
6.A
【分析】中心投影是指把光由一点向外散射形成的投影,平行投影是在一束平行光线照射下形成的投影,根据定义逐一分析即可得到答案.
【详解】解:太阳光线形成的投影是平行投影,
探照灯,手电筒,路灯形成的投影是中心投影,
故选A
【点睛】本题考查的是平行投影与中心投影的含义及应用,根据定义熟练判断中心投影与平行投影是解题的关键.
7.D
【分析】根据光线相交的是灯光光线,光线平行的不是灯光光线逐个判断.
【详解】连接并延长每个标杆影子的末端与标杆的顶端,射线相交的是灯光下形成的影子,不相交的不是灯光下形成的影子.
故选:D.
【点睛】本题考查了中心投影,熟练掌握中心投影的定义是解决此类问题的关键.
8.B
【分析】根据投影的性质:投影后的图像与投影前的图像相似,逐个判断即可得到答案;
【详解】解:由题意可得,
,
∴,故A错误,
,故B正确,
,故C,D不一定成立,
故选B;
【点睛】本题考查投影的性质:投影后的图像与投影前的图像相似.
9.A
【分析】根据中心投影的特点,当他从A点走到路灯下时,影长l逐渐变小,当从路灯下走到B点时,影长l逐渐变长,从而可对四个选项进行判断.
【详解】解:当他从A点走到路灯下时,影长l逐渐变小,当从路灯下走到B点时,影长l逐渐变长, 即随S的逐渐增大,l先由大变小,再由小变大,
故选:A.
【点睛】此题主要考查了函数图象以及中心投影的性质,得出l随s的变化规律是解决问题的关键.
10.D
【分析】根据平行投影的性质求解可得.
【详解】解:一张矩形纸片在太阳光线的照射下,形成影子可能是平行四边形、矩形、正方形,不可能是梯形,
故选D.
【点睛】本题主要考查平行投影,解题的关键是掌握平行投影的性质.
11.D
【分析】在同一路灯下由于位置不同,影长也不同;根据相关知识可解本题判断谁的影子长.
【详解】解: 张强的身高和李华的身高一样,在同一路灯下他们的影长与他们到路灯的距离有关,所以无法判断谁的影子长.
故选:D.
【点睛】本题综合考查了平行投影和中心投影的特点和规律,关键是要掌握好这规律;
12.B
【分析】正投影即投影线垂直于顶面产生的投影,据此直接选择即可.
【详解】光线由上向下照射,此正五棱柱的正投影是
故选:B.
【点睛】此题考查平行投影,解题关键此五棱柱的正投影与顶面的形状大小完全相同.
13.减小盲区
【分析】大型礼堂中为了后排观众能有更好的观看效果,而将前后排座位安排成阶梯状,是为了增大视角,减少盲区,可据此进行判断.
【详解】解:大型礼堂中的座位都呈阶梯状安放,可以增加后排观众的视角,减少盲区,以便得到更好的观看效果.
故答案为减小盲区.
【点睛】此题考查视角、盲区的相关知识,利用数学知识解决实际问题是中学数学的重要内容.
14.3
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似;
【详解】根据相同时刻的物高与影长成比例,设树的高度为,
则解得,
故这棵树的高是3米,
故答案为:3.
【点睛】本题主要考查同一时刻物高和影长成正比,考查利用所学知识解决实际问题的能力.
15.中心
【分析】根据中心投影的概念填写即可.中心投影是指把光由一点向外散射形成的投影.
【详解】解:路灯发出的光线可以看成是从一点发出的光线,像这样的光线所形成的投影叫做中心投影,故路灯下人的影子是中心投影.
故答案为:中心.
【点睛】本题主要考查了中心投影的概念,做题的关键是熟练掌握中心投影的概念,区别中心投影和平行投影概念.
16.
【分析】根据相似三角形的相似比等于对应高的比,列方程求出DE,进而求出OE,确定点E的坐标.
【详解】解:过点B作BF⊥x轴,垂足为F,
由题意得,BF=0.75,BC=1,
∵BCDE,
∴△ABC∽△ADE,
∴=,
即:,
解得:DE=1.6,
∴OE=2+1.6=3.6,
∴E(3.6,0),
故答案为:(3.6,0).
【点睛】考查中心投影的意义,将中心投影的问题转化为相似三角形的问题进行解答是常用的方法.
17. 投影 投影线 投影面
【解析】略
18.(1)线段CP为王乐在路灯B下的影子;(2)王乐站在Q处时,在路灯A下的影长为1.5m;(3)路灯A的高度为12m
【分析】(1)影长为光线与物高相交得到的阴影部分;
(2)易得Rt△CEP∽Rt△CBD,利用对应边成比例可得QD长;
(3)易得Rt△DFQ∽Rt△DAC,利用对应边成比例可得AC长,也就是路灯A的高度.
【详解】解:(1)线段CP为王乐在路灯B下的影子.
(2)由题意得Rt△CEP∽Rt△CBD,
∴,
解得:QD=1.5m.
所以王乐站在Q处时,在路灯A下的影长为1.5m
(3)由题意得Rt△QDF∽Rt△CDA,
∴,
∴,
解得:AC=12m.
所以路灯A的高度为12m.
【点睛】本题考查了中心投影及相似的判定和性质,利用两三角形相似,对应边成比例来求线段的长.
19.(1)详见解析
(2)4.8m
【分析】(1)连接并延长交于点,即为灯泡的位置,连接并延长,交于点,即为明的影子;
(2)根据相似三角形的判断和性质求出即可.
【详解】(1)解:如图点为灯泡,线段为小明的影子
(2)解:,,
,
,
,
灯泡的高度为.
【点睛】本题考查了作图—中心投影,相似三角形的判定和性质,解题的关键是根据题意画出图形,构造相似三角形,再根据相似三角形的性质求解.
20.
【分析】本题考查相似三角形的判定和性质,平行投影.先证,推出;再根据平行投影的性质,推出,,进而可得,代入数值求出,进而可得小雁塔的高度.
【详解】解:,,
,
又,
,
;
由平行投影可知,
,
又,
,
,
,即,
解得,
代入,得,
解得,
即小雁塔的高度为.
21.小亮身前的影长是米
【分析】本题主要考查了相似三角形的判定以及性质,连接并延长,与地面交于点E,再连接并延长,与地面交于点F,先设米,由,和都垂直于地面,可得出,,由相似三角形的性质得出,先求出的值,当米时,设小亮的影长是y米,由相似三角形的性质得出,代入即可求出y值,即小亮身前的影长.
【详解】解:如答图,连接并延长,与地面交于点E,再连接并延长,与地面交于点F,
先设米,
,和都垂直于地面,
∴,
,,
则当米时,米,
,即,
;
当米时,设小亮的影长是y米,
,
,
.
答:小亮身前的影长是米.
22.(1)的长为米
(2)明明应由点A前进米,亮亮恰好测得明明的影长是其身高的2倍
【分析】本题考查了相似三角形的应用;
(1)由题意首先判定,,然后根据相似三角形的对应边成比例解答;
(2)根据中心投影可得离点光源越远,则影长越长,设明明应由点A前进米,则,,可得,进而根据相似三角形的对应边成比例,即可求解.
【详解】(1)解:由题意知,则.
∴,即,
同理,,
∴,即,
解得:,
∴灯高的长为米;
(2)解:如图所示,依题意,
根据中心投影可得离点光源越远,则影长越长则明明应由点A前进,
设明明应由点A前进米,则,
依题意,
∴,
∴,
解得:,
答:明明应由点A前进米,亮亮恰好测得明明的影长是其身高的2倍.
23.(1),
(2)详见解析
(3)详见解析
【分析】(1)根据题意,即可得到答案;
(2)证明,得到,即可证明定理;
(3)利用射影定理,得到,,进而得到,即可证明.
【详解】(1)解:根据题意,图中线段的投影是,线段的投影是,
故答案为:,;
(2)证明:如图,
∵,,
∴,
而,
∴,
∴,
∴;
(3)证明:如图,
∵四边形为正方形,
∴,,
∴,
∵,
∴,
∴,
即,而,
∴
【点睛】本题考查了正方形的性质,相似三角形的判定和性质,勾股定理、射影定理等知识,解题关键是掌握相似三角形的判定和性质,理解射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.
24.(1)的投影是,的投影是点,的投影是
(2)证明过程见详解
(3)①证明过程见详解;②
【分析】(1)根据投影的定义,即可求解;
(2)根据中,,,可得,是公共角,由三角形相似的判定及性质即可求证;
(3)①根据射影定理可得,,且,根据三角形相似的判定方法即可求解;②先计算,,,的长度,在根据①中的结论即可求解.
【详解】(1)解:根据题意得,的投影是,的投影是点,的投影是.
(2)证明:∵中,,,
∴,,
∴,且是公共角,
∴,
∴,
∴.
(3)解:①证明:∵四边形是正方形,
∴,
∴,
中,
∵,,
∴,
∴,即,且(公共角),
∴;
②∵,且,
∴,,
在中,,
在中,,
∵,
∴,即,
∴.
【点睛】本题主要考查正方形,直角三角形,相似三角形的综合,掌握正方形的性质,直角三角形中判定三角形的相似,以及相似三角形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
29.1投影
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
2.晚上,王老师出去散步,他先走向一盏路灯,然后离路灯而去,他会发现自己的身影是( )
A.变长 B.变短 C.先变长后变短 D.先变短后变长
3.线段的长为a,线段在投影面P上的正投影的长度为b,则a,b的大小关系是( )
A.
B.
C.
D.
4.已知圆锥的底面的半径为3cm,母线长为5cm,则它的侧面积为
A.15πcm2 B.16πcm2 C.19πcm2 D.24πcm2
5.如图6, 已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是
A.24 B.30 C.48 D.60
6.下列哪种光线形成的投影是平行投影( )
A.太阳 B.探照灯 C.手电筒 D.路灯
7.如图所示是两根标杆在地面上的影子,根据这些投影,在灯光下形成的影子是( )
A.①和② B.②和④ C.③和④ D.②和③
8.幻灯机是教师常用的教具之一,它能把精致的图片投到银幕上,如图,在与中,下列结论一定正确的是( )
A. B. C. D.
9.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上他行走在这条路上如图,当他从点走到点的过程,他在灯光照射下的影长与所走路程的变化关系图象大致是( )
A. B. C. D.
10.一张矩形纸片在太阳光线的照射下,形成影子不可能是( )
A.平行四边形 B.矩形 C.正方形 D.梯形
11.张强的身高和李华的身高一样,那么在同一路灯下( )
A.小明的影子比小强的影子长 B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长 D.无法判断谁的影子长
12.一个正五棱柱如下图摆放,光线由上到下照射此正五棱柱时的正投影是( )
A. B. C. D.
二、填空题
13.大型礼堂中的座位都呈阶梯状安放,这样安放的道理是 .
14.如图,同一时刻小诚和大树的影子长分别为和,已知小诚身高,则大树的高度为 m.
15.路灯下行人的影子属于 投影.(填“平行”或“中心”)
16.小明家的客厅有一张直径为1米,高0.75米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中点D的坐标为,则点E的坐标是 .
17.一般地,用光线照射物体,在某个平面 (地面、墙壁等) 上得到的影子叫做物体的 .照射光线叫做 ,投影所在的平面叫做 .
三、解答题
18.如图,王乐同学在晩上由路灯走向路灯.当他行到处时发现,他往路灯下的影长为2m,且恰好位于路灯的正下方,接着他又走了到处,此时他在路灯下的影子恰好位于路灯的正下方(已知王乐身高,路灯高).
(1)王乐站在处时,在路灯下的影子是哪条线段?
(2)计算王乐站在处时,在路灯下的影长;
(3)计算路灯的高度.
19.小明晚上在路灯下的示意图如下,线段表示直立的灯杆,灯泡在其上端某处,线段表示一棵树,线段表示它在地面上的影子,线段表示小明.
(1)请确定灯泡所在的位置,并画出小明站在处的影子;
(2)若小明的身高,当小明离开灯杆的距离时,影子长为2.4m,求灯泡的高度.
20.小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.数学活动小组的同学对该塔进行了测量,测量方法如下:如图,小铭在小雁塔的影子顶端处竖直立一根木棒,并测得此时木棒的影长;然后,小希在的延长线上找出一点,使得、、三点在同一直线上,并测得.已知图中所有点均在同一平面内,木棒,,,请根据以上测量数据,求小雁塔的高度.
21.如图,是小亮晚上散步回家的场景,图中线段表示站立在路灯左侧的小亮,线段表示直立在地面上的路灯,点P表示照明灯的位置.当小亮与路灯之间的距离时,其身后的影长为,已知小亮的身高为,当小亮步行至路灯右侧且距路灯的点D处时,小亮身前的影长是多少米?(结果用分数表示)
22.如图,亮亮、明明利用家门口路灯的灯光来测量该路灯的高度,明明在A处时,亮亮测得明明的影长为2米,明明向前走2米到B处时,亮亮测得明明的影长为1米,已知明明的身高,为米,
(1)求路灯高
(2)在此路灯下,明明在直线上运动,明明应由点A前进或后退多少米,亮亮恰好测得明明的影长是其身高的2倍.
23.操作与研究:如图,被平行于的光线照射,于D,在投影面上.
(1)指出图中线段的投影是______,线段的投影是______.
(2)问题情景:如图1,中,,,我们可以利用与相似证明,这个结论我们称之为射影定理,请证明这个定理.
(3)拓展运用:如图2,正方形的边长为15,点O是对角线、的交点,点E在上,过点C作,垂足为F,连接;试利用射影定理证明;
24.操作与研究∶如图,被平行于的光线照射,于,在投影面上.
(1)指出图中的投影是什么,与的投影呢?
(2)探究∶ 如图1,中,,,我们可以利用与相似证明, 这个结论我们称之为射影定理,试证明这个定理.
(3)【结论运用】如图2,正方形的边长为,点是对角线的交点,点在上,过点作,垂足为,连接,
①试利用射影定理证明;
②若,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D A D A D B A D
题号 11 12
答案 D B
1.D
【分析】因为中心投影物体的高和影长成比例,正确的区分中心投影和平行投影,依次分析选项即可找到符合题意的选项
【详解】因为正方形的对角线互相垂直,且一条对角线垂直地面,光源与对角线组成的平面垂直于地面,则有影子的对角线仍然互相垂直,且由于光源在平板的上方,则上方的边长影子会更长一些,
故选D
【点睛】本题考查了中心投影的概念,应用,利用中心投影的特点,理解中心投影物体的高和影长成比例是解题的关键.
2.D
【分析】由题意可得王老师离光源是由远到近再到远的过程,根据中心投影的特点,即可得到身影的变化特点.
【详解】王老师经过一盏路灯的过程中,王老师离光源是由远到近再到远的过程,所以他在地上的影子先变短后变长.
故选D.
【点睛】本题考查了中心投影的特点和规律.中心投影的特点是:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
3.D
【分析】本题考查了平行投影,分三种情况考虑即可;
【详解】当线段平行于投影面放置时,;当线段倾斜于投影面放置时,;当线段垂直于投影面放置时,.
综上知,.
故选D
4.A
【详解】试题分析:S==15π.
考点:圆锥的侧面积计算.
5.D
【详解】由图可知,圆锥半径为6,高为8,∴母线长为10,∴圆锥的侧面积是=
==,故选D
6.A
【分析】中心投影是指把光由一点向外散射形成的投影,平行投影是在一束平行光线照射下形成的投影,根据定义逐一分析即可得到答案.
【详解】解:太阳光线形成的投影是平行投影,
探照灯,手电筒,路灯形成的投影是中心投影,
故选A
【点睛】本题考查的是平行投影与中心投影的含义及应用,根据定义熟练判断中心投影与平行投影是解题的关键.
7.D
【分析】根据光线相交的是灯光光线,光线平行的不是灯光光线逐个判断.
【详解】连接并延长每个标杆影子的末端与标杆的顶端,射线相交的是灯光下形成的影子,不相交的不是灯光下形成的影子.
故选:D.
【点睛】本题考查了中心投影,熟练掌握中心投影的定义是解决此类问题的关键.
8.B
【分析】根据投影的性质:投影后的图像与投影前的图像相似,逐个判断即可得到答案;
【详解】解:由题意可得,
,
∴,故A错误,
,故B正确,
,故C,D不一定成立,
故选B;
【点睛】本题考查投影的性质:投影后的图像与投影前的图像相似.
9.A
【分析】根据中心投影的特点,当他从A点走到路灯下时,影长l逐渐变小,当从路灯下走到B点时,影长l逐渐变长,从而可对四个选项进行判断.
【详解】解:当他从A点走到路灯下时,影长l逐渐变小,当从路灯下走到B点时,影长l逐渐变长, 即随S的逐渐增大,l先由大变小,再由小变大,
故选:A.
【点睛】此题主要考查了函数图象以及中心投影的性质,得出l随s的变化规律是解决问题的关键.
10.D
【分析】根据平行投影的性质求解可得.
【详解】解:一张矩形纸片在太阳光线的照射下,形成影子可能是平行四边形、矩形、正方形,不可能是梯形,
故选D.
【点睛】本题主要考查平行投影,解题的关键是掌握平行投影的性质.
11.D
【分析】在同一路灯下由于位置不同,影长也不同;根据相关知识可解本题判断谁的影子长.
【详解】解: 张强的身高和李华的身高一样,在同一路灯下他们的影长与他们到路灯的距离有关,所以无法判断谁的影子长.
故选:D.
【点睛】本题综合考查了平行投影和中心投影的特点和规律,关键是要掌握好这规律;
12.B
【分析】正投影即投影线垂直于顶面产生的投影,据此直接选择即可.
【详解】光线由上向下照射,此正五棱柱的正投影是
故选:B.
【点睛】此题考查平行投影,解题关键此五棱柱的正投影与顶面的形状大小完全相同.
13.减小盲区
【分析】大型礼堂中为了后排观众能有更好的观看效果,而将前后排座位安排成阶梯状,是为了增大视角,减少盲区,可据此进行判断.
【详解】解:大型礼堂中的座位都呈阶梯状安放,可以增加后排观众的视角,减少盲区,以便得到更好的观看效果.
故答案为减小盲区.
【点睛】此题考查视角、盲区的相关知识,利用数学知识解决实际问题是中学数学的重要内容.
14.3
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似;
【详解】根据相同时刻的物高与影长成比例,设树的高度为,
则解得,
故这棵树的高是3米,
故答案为:3.
【点睛】本题主要考查同一时刻物高和影长成正比,考查利用所学知识解决实际问题的能力.
15.中心
【分析】根据中心投影的概念填写即可.中心投影是指把光由一点向外散射形成的投影.
【详解】解:路灯发出的光线可以看成是从一点发出的光线,像这样的光线所形成的投影叫做中心投影,故路灯下人的影子是中心投影.
故答案为:中心.
【点睛】本题主要考查了中心投影的概念,做题的关键是熟练掌握中心投影的概念,区别中心投影和平行投影概念.
16.
【分析】根据相似三角形的相似比等于对应高的比,列方程求出DE,进而求出OE,确定点E的坐标.
【详解】解:过点B作BF⊥x轴,垂足为F,
由题意得,BF=0.75,BC=1,
∵BCDE,
∴△ABC∽△ADE,
∴=,
即:,
解得:DE=1.6,
∴OE=2+1.6=3.6,
∴E(3.6,0),
故答案为:(3.6,0).
【点睛】考查中心投影的意义,将中心投影的问题转化为相似三角形的问题进行解答是常用的方法.
17. 投影 投影线 投影面
【解析】略
18.(1)线段CP为王乐在路灯B下的影子;(2)王乐站在Q处时,在路灯A下的影长为1.5m;(3)路灯A的高度为12m
【分析】(1)影长为光线与物高相交得到的阴影部分;
(2)易得Rt△CEP∽Rt△CBD,利用对应边成比例可得QD长;
(3)易得Rt△DFQ∽Rt△DAC,利用对应边成比例可得AC长,也就是路灯A的高度.
【详解】解:(1)线段CP为王乐在路灯B下的影子.
(2)由题意得Rt△CEP∽Rt△CBD,
∴,
解得:QD=1.5m.
所以王乐站在Q处时,在路灯A下的影长为1.5m
(3)由题意得Rt△QDF∽Rt△CDA,
∴,
∴,
解得:AC=12m.
所以路灯A的高度为12m.
【点睛】本题考查了中心投影及相似的判定和性质,利用两三角形相似,对应边成比例来求线段的长.
19.(1)详见解析
(2)4.8m
【分析】(1)连接并延长交于点,即为灯泡的位置,连接并延长,交于点,即为明的影子;
(2)根据相似三角形的判断和性质求出即可.
【详解】(1)解:如图点为灯泡,线段为小明的影子
(2)解:,,
,
,
,
灯泡的高度为.
【点睛】本题考查了作图—中心投影,相似三角形的判定和性质,解题的关键是根据题意画出图形,构造相似三角形,再根据相似三角形的性质求解.
20.
【分析】本题考查相似三角形的判定和性质,平行投影.先证,推出;再根据平行投影的性质,推出,,进而可得,代入数值求出,进而可得小雁塔的高度.
【详解】解:,,
,
又,
,
;
由平行投影可知,
,
又,
,
,
,即,
解得,
代入,得,
解得,
即小雁塔的高度为.
21.小亮身前的影长是米
【分析】本题主要考查了相似三角形的判定以及性质,连接并延长,与地面交于点E,再连接并延长,与地面交于点F,先设米,由,和都垂直于地面,可得出,,由相似三角形的性质得出,先求出的值,当米时,设小亮的影长是y米,由相似三角形的性质得出,代入即可求出y值,即小亮身前的影长.
【详解】解:如答图,连接并延长,与地面交于点E,再连接并延长,与地面交于点F,
先设米,
,和都垂直于地面,
∴,
,,
则当米时,米,
,即,
;
当米时,设小亮的影长是y米,
,
,
.
答:小亮身前的影长是米.
22.(1)的长为米
(2)明明应由点A前进米,亮亮恰好测得明明的影长是其身高的2倍
【分析】本题考查了相似三角形的应用;
(1)由题意首先判定,,然后根据相似三角形的对应边成比例解答;
(2)根据中心投影可得离点光源越远,则影长越长,设明明应由点A前进米,则,,可得,进而根据相似三角形的对应边成比例,即可求解.
【详解】(1)解:由题意知,则.
∴,即,
同理,,
∴,即,
解得:,
∴灯高的长为米;
(2)解:如图所示,依题意,
根据中心投影可得离点光源越远,则影长越长则明明应由点A前进,
设明明应由点A前进米,则,
依题意,
∴,
∴,
解得:,
答:明明应由点A前进米,亮亮恰好测得明明的影长是其身高的2倍.
23.(1),
(2)详见解析
(3)详见解析
【分析】(1)根据题意,即可得到答案;
(2)证明,得到,即可证明定理;
(3)利用射影定理,得到,,进而得到,即可证明.
【详解】(1)解:根据题意,图中线段的投影是,线段的投影是,
故答案为:,;
(2)证明:如图,
∵,,
∴,
而,
∴,
∴,
∴;
(3)证明:如图,
∵四边形为正方形,
∴,,
∴,
∵,
∴,
∴,
即,而,
∴
【点睛】本题考查了正方形的性质,相似三角形的判定和性质,勾股定理、射影定理等知识,解题关键是掌握相似三角形的判定和性质,理解射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.
24.(1)的投影是,的投影是点,的投影是
(2)证明过程见详解
(3)①证明过程见详解;②
【分析】(1)根据投影的定义,即可求解;
(2)根据中,,,可得,是公共角,由三角形相似的判定及性质即可求证;
(3)①根据射影定理可得,,且,根据三角形相似的判定方法即可求解;②先计算,,,的长度,在根据①中的结论即可求解.
【详解】(1)解:根据题意得,的投影是,的投影是点,的投影是.
(2)证明:∵中,,,
∴,,
∴,且是公共角,
∴,
∴,
∴.
(3)解:①证明:∵四边形是正方形,
∴,
∴,
中,
∵,,
∴,
∴,即,且(公共角),
∴;
②∵,且,
∴,,
在中,,
在中,,
∵,
∴,即,
∴.
【点睛】本题主要考查正方形,直角三角形,相似三角形的综合,掌握正方形的性质,直角三角形中判定三角形的相似,以及相似三角形的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
