第二十八章 锐角三角函数同步练习(含解析)
文档属性
| 名称 | 第二十八章 锐角三角函数同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 20:39:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二十八章锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题正确的是( )
A.对角线相等四边形是矩形
B.相似三角形的面积比等于相似比
C.在反比例函数图像上,随的增大而增大
D.若一个斜坡的坡度为,则该斜坡的坡角为
2.位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 进行了测量.如图,他们从塔底的点出发,沿水平方向行走了米,到达点,然后沿斜坡继续前进到达点处,已知.在点处用测角仪测得塔顶的仰角为(点,,,,在同一平面内).其中测角仪及其支架高度约为米,斜坡的坡度(或坡比),那么文峰塔的高度约为( )
A.22.5 米 B.24.0 米 C.28.0 米 D.33.3 米
3.如图,为了测量河岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=50°,那么AB等于( )
A.asin50° B.atan50° C.acos50° D.
4.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进16m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A. B. C. D.
5.有一题目:已知外接圆的半径为2,,求的度数.
嘉嘉这样求解:如图,作直径,点在上,∵为直径,∴,在中,∵,∴,∴.
琪琪说:“嘉嘉的答案不全,还有一个不同的值.”
下列判断正确的是( )
A.嘉嘉的答案没有遗漏 B.嘉嘉的结果错误,
C.琪琪的说法错误 D.琪琪的说法正确,还有一个答案为120°
6.如图,在△ABC中,∠A=120°,AB=4,AC=2,则tanB的值是( )
A. B. C. D.
7.如图,平面直角坐标系中有点A(-2,0),直线交轴于点,,直线轴,垂足为D(3,0),点为直线上一点,如果,则点坐标为( )
A. B. C. D.
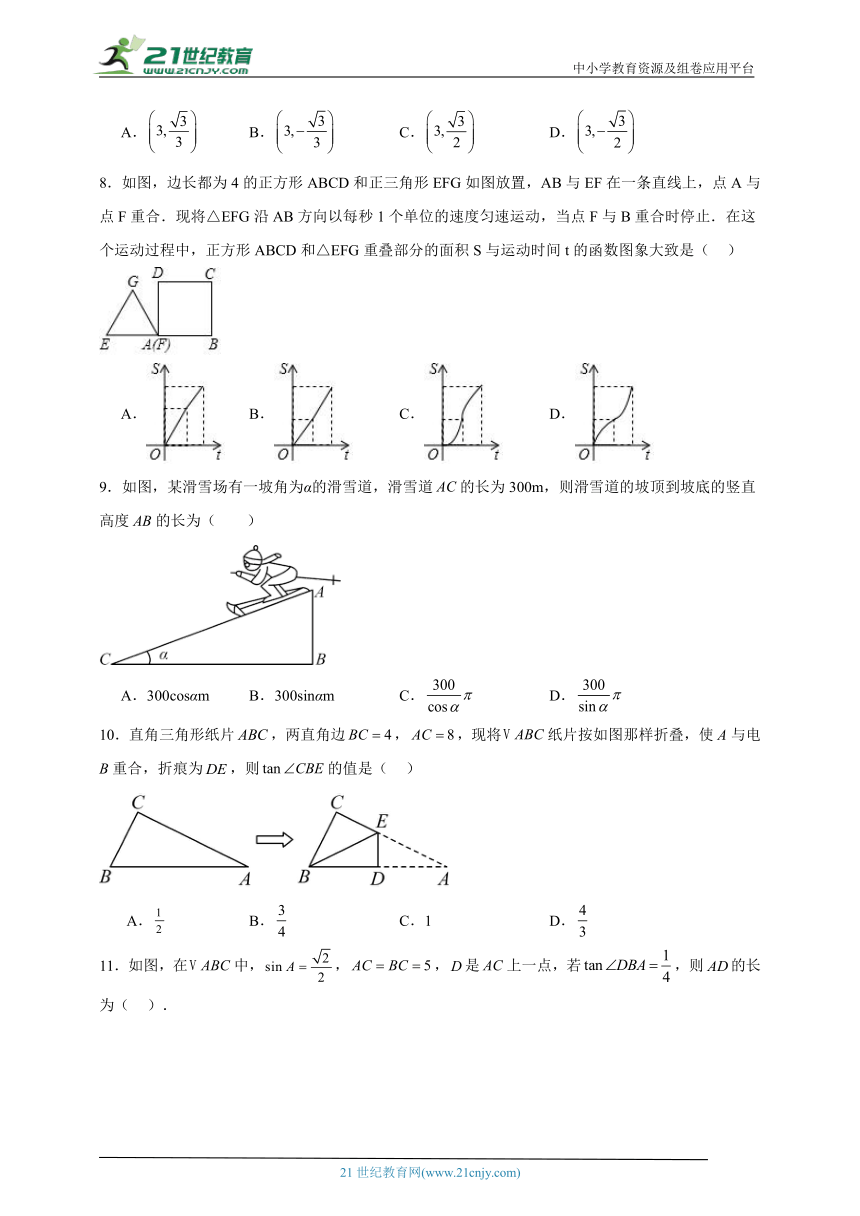
8.如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
A. B. C. D.
9.如图,某滑雪场有一坡角为α的滑雪道,滑雪道的长为300m,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A.300cosαm B.300sinαm C. D.
10.直角三角形纸片,两直角边,,现将纸片按如图那样折叠,使A与电B重合,折痕为,则的值是( )
A. B. C.1 D.
11.如图,在中,,,是上一点,若,则的长为( ).
A. B. C. D.
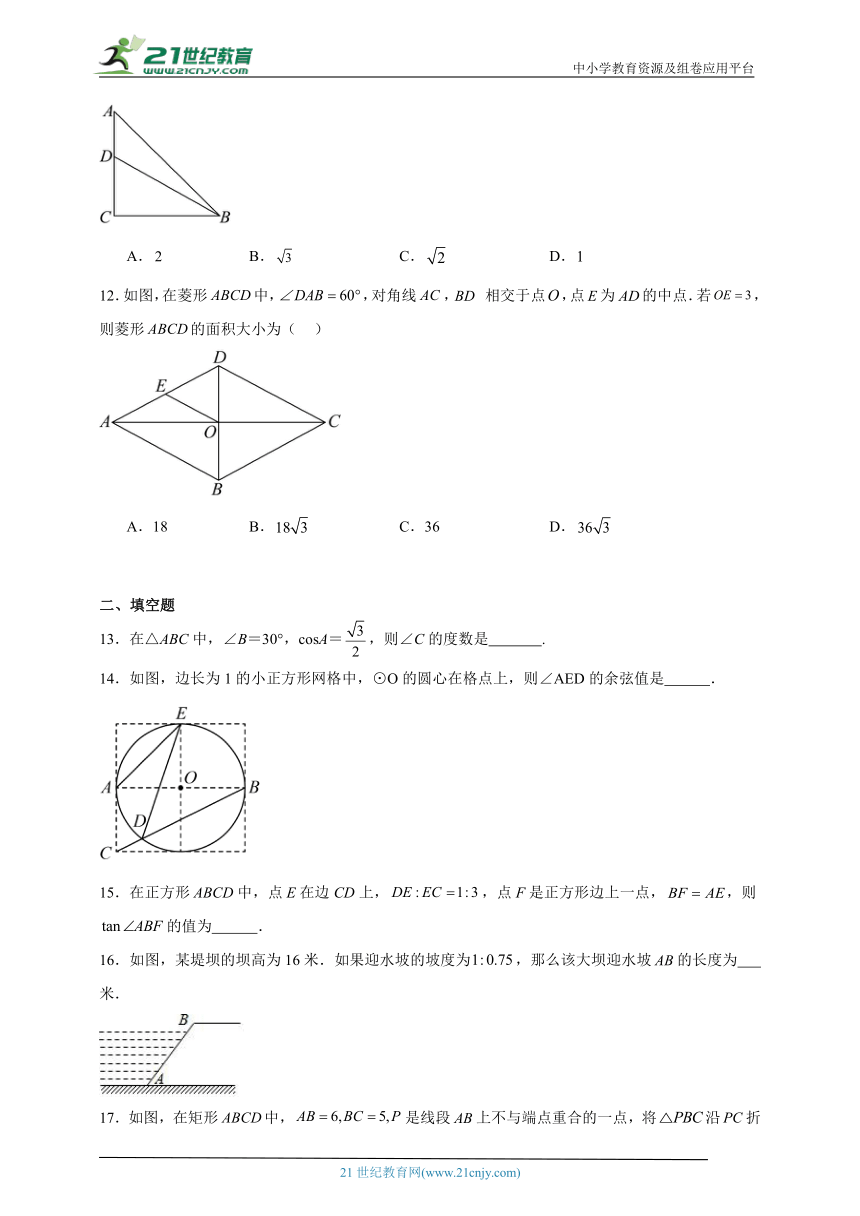
12.如图,在菱形中,,对角线, 相交于点,点为的中点.若,则菱形的面积大小为( )
A.18 B. C.36 D.
二、填空题
13.在△ABC中,∠B=30°,cosA=,则∠C的度数是 .
14.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是 .
15.在正方形ABCD中,点E在边CD上,,点F是正方形边上一点,,则的值为 .
16.如图,某堤坝的坝高为16米.如果迎水坡的坡度为,那么该大坝迎水坡的长度为 米.
17.如图,在矩形中,是线段上不与端点重合的一点,将沿折叠得对应,当点落在矩形的对称轴上时,的长为 .
三、解答题
18.计算:
(1)
(2)
19.如图,是由边长为1的小正方形构成的网格,各个小正方形的顶点称之为格点,点A、C、E、F、M、N均在格点上,根据不同要求,选择格点,画出符合条件的图形;
(1)在图1中,画以AC为一边的△CAB,使∠CAB=45°,点B在小正方形的格点上;
(2)在图2中,画一个以EF为腰的等腰△DEF,使,点D在小正方形的格点上;
(3)在图3中,画一个以MN为一边的△MNP,使tan∠MNP=,点P在小正方形的格点上.
20.综合与实践
某校数学兴趣小组测量校内旗杆的高度,活动记录如下:
活动任务:测量旗杆的高度 【步骤一】设计测量方案小组成员讨论后,画出两种测量方案的图形,如图1,图2.
【步骤二】准备测量工具镜子,皮尺和测倾器,如图3.皮尺的功能是直接测量任意可达到的两点间的距离;测倾器(由度盘,铅锤和支杆组成)的功能是测量目标物的仰角或俯角.(如图3)
【步骤三】实地测量并记录数据 方案一:利用镜子的反射(测量时,所使用的平面镜的大小和厚度均忽略不计,根据光的反射定律,反射角等于入射角,法线,),如图1,小明利用镜子和皮尺测出了旗杆的高度,其测量和求解过程如下: 测量过程: 小明将镜子放在距离旗杆底部的点C处,然后看着镜子沿直线来回移动,直至看到旗杆顶端B在镜子中的像与点C重合,此时小明站在点D处,测得,小明的眼睛离地面的高度. 求解过程: 由测量知,,,. ∵法线,, ∴ ∵①______, ∴. ∴,即. ∴②______().故旗杆的高度为③_______. 方案二:如图2,小亮在测点D处安置测倾器,测得旗杆顶端B的仰角,量出测点D到旗杆的距离,量出测倾器的高度.
(1)补全小明求解过程中①②③所缺的内容;
(2)请你根据方案二求出旗杆的高度(结果精确到).(参考数据:,,)
21.河南周口的高贤寿圣寺塔保存完整,是第七批全国重点文物保护单位.如图所示,高贤寿圣寺塔后有一坡比为的土坡,某测量小组在D点架设测角仪,测得塔顶A的仰角为,已知土坡长为米,坡脚C与塔基B的水平距离米,求高贤寿圣寺塔的高度.
(结果精确到1米,参考数据:,,,)
22.图1是一种阅读支架,图2是其侧面示意图,托板、支撑杆可分别绕点B,D 转动,B 为的中点.研究发现,阅读最佳视觉角度是眼视线与水平面夹角为,小涵想要以此视角使用阅读支架.已知支撑杆长,其与桌面夹角,托板长,点E 是小涵眼睛的位置,是小涵阅读书本的视线,于点F,小涵眼睛与桌面的距离为.请你计算的长度.
(结果精确到,参考数据: )
23.如图,点O为矩形ABCD的对角线AC上一点,以OA为半径的⊙O交AD于点E,交AC于点F,且.
(1)求证:直线CE是⊙O的切线;
(2)若,,求⊙O的半径.
24.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE,
(1)求证:△ABE≌△DFA.
(2)如果AD=10,AB=6,求sin∠EDF的值.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B A D D B C B B
题号 11 12
答案 A B
1.D
【分析】根据矩形的判断定理、相似三角形的性质、反比例函数的性质、坡度的定义及特殊的三角函数值解答即可.
【详解】对角线相等的平行四边形是矩形,故A错误;
相似三角形的面积比等于相似比的平方,故B错误;
在反比例函数图像上,在每个象限内,随的增大而增大,故C错误;
若一个斜坡的坡度为,则tan坡角= ,该斜坡的坡角为,故D正确.
故选:D
【点睛】本题考查的是矩形的判断定理、相似三角形的性质、反比例函数的性质、坡度的定义及特殊的三角函数值,熟练的掌握各图形及函数的性质是关键.
2.C
【详解】过点E作EM⊥AB于点M,
∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=13米,
∴设DG=x,则CG=2.4x.
在Rt△CDG中,∵,即 解得x=5,
∴DG=5米,CG=12米,
∴EG=5+0.5=5.5米,BG=13+12=25米,
∵EM⊥AB,AB⊥BG,EG⊥BG,
∴四边形EGBM是矩形,
∴EM=BG=25米,BM=EG=5.5米,
在Rt△AEM中,
∵
∴米,
∴AB=AM+BM=22.5+5.5=28米.
故选C.
3.B
【分析】根据题意,可得Rt△ABC,同时可知AC与∠ACB.根据三角函数的定义解答.
【详解】根据题意,在Rt△ABC,有AC=a,∠ACB=50°,且tan50°=,
则AB=AC×tan50°=a tan50°,
故选B.
【点睛】本题考查了解直角三角形的应用,要熟练掌握三角函数的定义.
4.A
【分析】利用所给的角的三角函数用AB表示出BD,CB;根据BC﹣DB=CD即可求出建筑物AB的高度.
【详解】解:∵在Rt△ABC中,∠ACB=30°,
∴tan∠ACB=tan30°=,
∴BC==AB,
∵在Rt△ABD中,∠ADB=45°,
∴tan∠ADB=tan45°=,
∴BD==AB.
∵CD=BC﹣BD=16,
∴AB﹣AB=16,
解得:AB=8(+1)m.
故选:A.
【点睛】本题考查了仰角问题,解决此类问题的关键是正确的将仰角转化为直角三角形的内角并选择正确的边角关系解直角三角形.
5.D
【分析】分两种情况,根据圆周角定理和圆内接四边形的性质求解即可.
【详解】解:情形一、如图,作直径,连接DB,点A在上,
∵为直径,半径为2,
∴CD=4,,
在中,∵,CD=4
∴,
∴,
∴.
情形二:如图,作直径,连接DB,点A在劣弧上,
∵为直径,半径为2,
∴CD=4,,
在中,∵,CD=4
∴,
∴,
∵四边形ABDC是圆的内接四边形,
∴
∴
∴琪琪的说法正确,还有一个答案为120°
故选:D
【点睛】本题考查了圆周角定理,圆内接四边形的性质以及解直角三角形等知识点,能综合运用知识点进行推理是解此题的关键.
6.D
【分析】先求出120°的补角为60°,然后再把60°放在直角三角形中,所以过点C作CD⊥AB,交BA的延长线于点D,在Rt△ACD中可求出AD与CD的长,最后在Rt△BDC中利用勾股定理求出BC即可解答.
【详解】解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠CAD=180°-∠BAC=60°,
在Rt△ACD中,AC=2,
∴AD=ACcos60°=2×=1,
CD=ACsin60°=2×=,
∵AB=4,
∴BD=AB+AD=4+1=5,
∴tanB=,
故选:D.
【点睛】本题考查了解直角三角形,勾股定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.B
【分析】根据题意可求出点B坐标,设点C的坐标为(3,t),根据CA=CB,利用两点间的距离公式,列出关系式,求出t的值,即可求出点C的坐标.
【详解】解:∵点A(-2,0),直线交轴于点,,
∴,
∴,
∴点B的坐标为(0,),
设点C的坐标为(3,t),
∵CA=CB,
∴,
解得,
∴点C的坐标为.
故选:B.
【点睛】本题主要考查坐标与图形性质,熟练掌握直角三角形的性质、两点间的距离公式是解答此题的关键.
8.C
【分析】根据题意和函数图象可以写出各段对应的函数解析式,从而可以判断哪个选项中的图象符合题意,本题得以解决.
【详解】解:当时,,即S与t是二次函数关系,有最小值,开口向上,
当时,,即S与t是二次函数关系,开口向下,
由上可得,选项C符合题意,
故选C.
【点睛】考查动点问题的函数过图象,解答本题的关键是明确题意,利用数形结合的思想解答.
9.B
【分析】
本题考查了解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念,熟记锐角三角函数的定义是解题的关键.
根据正弦的定义进行解答即可.
【详解】
解:在中,,,,
∵,
∴,
故选:B.
10.B
【分析】根据折叠的性质得出,设,则,在中,根据勾股定理得出,列出方程求出x的值,最后根据正切的定义,即可解答.
【详解】解:∵沿折叠得到,
∴,
设,则,
在中,根据勾股定理可得:,
即,解得:,
∴,
故选:B.
【点睛】本题主要考查了折叠的性质,勾股定理,正切的定义,解题的关键是掌握折叠前后对应边相等.
11.A
【分析】本题考查了解直角三角形,在直角三角形中,由已知元素求未知元素的过程就是解直角三角形,也考查了等腰直角三角形的性质,作于,由,得,根据等腰直角三角形的性质得到 ,设则,,在中,利用的正切得到,然后由可计算出 ,再利用 ,进行计算即可,解题的关键是添加辅助线构造直角三角形,再利用三角函数求边长.
【详解】作于,如图,
∵,
∴,
∵,
∴,
∴,是等腰直角三角形,
∴,
在中,设,则,
则,
在中,,
∴,
∴,解得:,
∴,
故选:.
12.B
【分析】
由菱形的性质可为直角三角形,根据锐角三角函数值得到、,求、的长,由菱形的面积公式可求解.
【详解】
解:∵四边形是菱形,
,,
为直角三角形,
点为的中点,,
,
,
,
,
,
,
,
∴菱形的面积=
故选:B.
【点睛】本题考查了菱形的性质,锐角三角函数,熟练运用菱形面积公式是本题的关键.
13.120°/120度
【分析】根据特殊角的三角函数值求出∠A的度数,然后根据三角形的内角和求解即可.
【详解】解:∵cosA=,
∴∠A=30 ,
∵∠B=30°,
∴∠C=180 -∠A-∠B=120 .
故答案为120°.
【点睛】此题主要考查了特殊角的三角函数值的应用,关键是熟记三角函数值和角的度数之间的关系,比较简单.
14.
【详解】试题分析:∵∠AED与∠ABC都对,
∴∠AED=∠ABC,
在Rt△ABC中,AB=2,AC=1,
根据勾股定理得:BC=,
则cos∠AED=cos∠ABC= =.
考点:1.圆周角定理;2.勾股定理;3.锐角三角函数的定义.
15.或4
【分析】由正方形的性质得出BC=AB=AD=CD=DE+EC,∠BAD=∠C=∠D=90°;分两种情况:①当点F在AD边上时,求出tan∠ABF即可;②当点F在CD边上时,求出tan∠ABF.
【详解】解:∵四边形ABCD是正方形,
∴AB=AD=CD=DE+EC,∠BAD=∠C=∠D=90°,,
∵,
∴设,则,BC=AB=AD=CD=4x;
分两种情况:
①当点F在AD边上时,如图所示:
在和中,
,
,
,
;
②当点F在CD边上时,如图所示:
在和中,
,
,
,
,
,
;
故答案为:或.
【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,正切的定义,熟练掌握正方形的性质,正切的定义是解题的关键.
16.20
【分析】根据坡度是坡面的铅直高度和水平宽度的比,再根据勾股定理即可求出该大坝迎水坡AB的长度.
【详解】解:如图,过点B作BC垂直于水平面于点C,可知BC=16米,
∵BC:AC=1:0.75,
∴16:AC=1:0.75,
∴AC=12(米),
∴AB==20(米),
答:该大坝迎水坡AB的长度为20米.
故答案为:20.
【点睛】本题考查了解直角三角形的应用-坡度坡角问题,解决本题的关键是掌握坡度坡角定义.
17.或
【分析】本题考查了矩形的性质,勾股定理,折叠性质,解答时分店E落在横对称轴上和纵对称轴上,两种情况计算即可,采用分类讨论的思想是解此题的关键.
【详解】如图当点E落在对称上时,
∵ 矩形中,,沿折叠得对应,
∴,,,
,
∴,,,
设,则,
∴,
解得;
如图当点E落在对称上时,设的交点为Q,
∵ 矩形中,,沿折叠得对应,
∴,,
,
∴,
∴,
∴,
∴是等边三角形,
∴,,,
∴,
∴,
故答案为:或.
18.(1)1
(2)
【分析】本题主要考查了锐角三角函数的混合运算:
(1)先把特殊角锐角三角函数值代入,再计算,即可求解;
(2)先把特殊角锐角三角函数值代入,再计算,即可求解.
【详解】(1)解:
(2)解:
19.(1)见解析;
(2)见解析;
(3)见解析
【分析】(1)利用网格特点,构造△ABC是以AB为底的等腰直角三角形即可;
(2)根据等腰三角形的定义画出即可;
(3)由于tan∠MNP=,则在含∠MNP的直角三角形中,满足对边与邻边之比为1:2即可.
【详解】(1)解:如图1,△ABC为所作:
∵AC=,,,
∴,,
∴△ABC是以AB为斜边的等腰直角三角形,
∴∠CAB=45°,
即△CAB满足要求;
(2)如图2所示:
由勾股定理得,,
∴DE=EF=5,
∴△DEF是等腰三角形,
∵,
∴△DEF满足要求;
(3)如图3所示:
∵,,,
∴
∴△MNP是以MN为斜边的直角三角形,
∴,
即作图符合要求.
【点睛】本题考查了勾股定理及其逆定理、锐角三角比、等腰直角三角形的判定和性质等知识,熟练掌握勾股定理及其逆定理是解题的关键.
20.(1)①(或);②;③
(2)旗杆的高度约为
【分析】(1)本题考查相似三角形的性质与判定,根据题意证明,再利用相似三角形对应边成比例,建立等式求解,即可解题.
(2)本题考查解直角三角形,根据题意得出、,利用,求得,再根据,即可解题.
【详解】(1)解:由测量知,,,,
法线,,
,
,
,
,即,
,
故旗杆的高度为.
故答案为:(或);;;
(2)解:由题知,,,,,
,,
,
,即,解得,
,
旗杆的高度约为.
21.28米
【分析】本题考查了解直角三角形的应用的仰俯角问题,熟练掌握锐角三角函数与边的关系是解题的关键;
过点D分别作于点E,于点F.得四边形是矩形,
在中,根据坡比为,求出(米),(米),,在中,,求出,即可得出塔的高度.
【详解】解:过点D分别作于点E,于点F.
∴四边形是矩形.
∴,.
在中,
∵,
∴,.
∴(米),(米).
∴(米).
在中,,
∴(米).
∴(米).
答:高贤寿圣寺塔AB的高度约为28米.
22.
【分析】本题考查解直角三角形的实际应用,矩形的判定和性质等知识,过点B作,垂足分别为,即得出四边形是矩形,;结合题意,,从而求得,进面可求,最的根据求解即可.
【详解】解:如图,过点B作,垂足分别为.
,
四边形是矩形,
,
在中,,
,
,
,
,
,
在中,,
,
,
.
23.(1)见解析;(2)
【分析】(1)根据矩形的性质及,证明即可;
(2)过点O作于点H,由(1)的结论及求出,继而在中用勾股定理即可求得半径.
【详解】(1)证明:连接OE,
∵矩形ABCD中,,
,
∴,,
,,
∵,
∴,
∴,
∵,
∴,∴,
又∵OE为⊙O半径CE过点E,∴直线CE是⊙O的切线.
(2)过点O作于点H,
则,
∵,,
∴,
∴,
∴,
∴,
在中,
.
【点睛】本题考查了矩形的性质,圆的切线的判定与性质,锐角三角函数,勾股定理,正确的作出辅助线是解题的关键.
24.(1)证明见解析;(2).
【分析】(1)根据矩形的对边平行且相等得到AD=BC=AE,∠DAF=∠AEB.再结合一对直角相等即可证明三角形全等;
(2)根据全等三角形的对应边相等以及勾股定理,可以求得DF,EF的长;再根据勾股定理求得DE的长,运用三角函数定义求解.
【详解】(1)在矩形中,,
.
,
,.
.
(2)由(1)知.
.
在直角中,,
.
在Rt中,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十八章锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题正确的是( )
A.对角线相等四边形是矩形
B.相似三角形的面积比等于相似比
C.在反比例函数图像上,随的增大而增大
D.若一个斜坡的坡度为,则该斜坡的坡角为
2.位于南岸区黄桷垭的文峰塔,有着“平安宝塔”之称.某校数学社团对其高度 进行了测量.如图,他们从塔底的点出发,沿水平方向行走了米,到达点,然后沿斜坡继续前进到达点处,已知.在点处用测角仪测得塔顶的仰角为(点,,,,在同一平面内).其中测角仪及其支架高度约为米,斜坡的坡度(或坡比),那么文峰塔的高度约为( )
A.22.5 米 B.24.0 米 C.28.0 米 D.33.3 米
3.如图,为了测量河岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=50°,那么AB等于( )
A.asin50° B.atan50° C.acos50° D.
4.如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进16m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB的高度等于( )
A. B. C. D.
5.有一题目:已知外接圆的半径为2,,求的度数.
嘉嘉这样求解:如图,作直径,点在上,∵为直径,∴,在中,∵,∴,∴.
琪琪说:“嘉嘉的答案不全,还有一个不同的值.”
下列判断正确的是( )
A.嘉嘉的答案没有遗漏 B.嘉嘉的结果错误,
C.琪琪的说法错误 D.琪琪的说法正确,还有一个答案为120°
6.如图,在△ABC中,∠A=120°,AB=4,AC=2,则tanB的值是( )
A. B. C. D.
7.如图,平面直角坐标系中有点A(-2,0),直线交轴于点,,直线轴,垂足为D(3,0),点为直线上一点,如果,则点坐标为( )
A. B. C. D.
8.如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
A. B. C. D.
9.如图,某滑雪场有一坡角为α的滑雪道,滑雪道的长为300m,则滑雪道的坡顶到坡底的竖直高度AB的长为( )
A.300cosαm B.300sinαm C. D.
10.直角三角形纸片,两直角边,,现将纸片按如图那样折叠,使A与电B重合,折痕为,则的值是( )
A. B. C.1 D.
11.如图,在中,,,是上一点,若,则的长为( ).
A. B. C. D.
12.如图,在菱形中,,对角线, 相交于点,点为的中点.若,则菱形的面积大小为( )
A.18 B. C.36 D.
二、填空题
13.在△ABC中,∠B=30°,cosA=,则∠C的度数是 .
14.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是 .
15.在正方形ABCD中,点E在边CD上,,点F是正方形边上一点,,则的值为 .
16.如图,某堤坝的坝高为16米.如果迎水坡的坡度为,那么该大坝迎水坡的长度为 米.
17.如图,在矩形中,是线段上不与端点重合的一点,将沿折叠得对应,当点落在矩形的对称轴上时,的长为 .
三、解答题
18.计算:
(1)
(2)
19.如图,是由边长为1的小正方形构成的网格,各个小正方形的顶点称之为格点,点A、C、E、F、M、N均在格点上,根据不同要求,选择格点,画出符合条件的图形;
(1)在图1中,画以AC为一边的△CAB,使∠CAB=45°,点B在小正方形的格点上;
(2)在图2中,画一个以EF为腰的等腰△DEF,使,点D在小正方形的格点上;
(3)在图3中,画一个以MN为一边的△MNP,使tan∠MNP=,点P在小正方形的格点上.
20.综合与实践
某校数学兴趣小组测量校内旗杆的高度,活动记录如下:
活动任务:测量旗杆的高度 【步骤一】设计测量方案小组成员讨论后,画出两种测量方案的图形,如图1,图2.
【步骤二】准备测量工具镜子,皮尺和测倾器,如图3.皮尺的功能是直接测量任意可达到的两点间的距离;测倾器(由度盘,铅锤和支杆组成)的功能是测量目标物的仰角或俯角.(如图3)
【步骤三】实地测量并记录数据 方案一:利用镜子的反射(测量时,所使用的平面镜的大小和厚度均忽略不计,根据光的反射定律,反射角等于入射角,法线,),如图1,小明利用镜子和皮尺测出了旗杆的高度,其测量和求解过程如下: 测量过程: 小明将镜子放在距离旗杆底部的点C处,然后看着镜子沿直线来回移动,直至看到旗杆顶端B在镜子中的像与点C重合,此时小明站在点D处,测得,小明的眼睛离地面的高度. 求解过程: 由测量知,,,. ∵法线,, ∴ ∵①______, ∴. ∴,即. ∴②______().故旗杆的高度为③_______. 方案二:如图2,小亮在测点D处安置测倾器,测得旗杆顶端B的仰角,量出测点D到旗杆的距离,量出测倾器的高度.
(1)补全小明求解过程中①②③所缺的内容;
(2)请你根据方案二求出旗杆的高度(结果精确到).(参考数据:,,)
21.河南周口的高贤寿圣寺塔保存完整,是第七批全国重点文物保护单位.如图所示,高贤寿圣寺塔后有一坡比为的土坡,某测量小组在D点架设测角仪,测得塔顶A的仰角为,已知土坡长为米,坡脚C与塔基B的水平距离米,求高贤寿圣寺塔的高度.
(结果精确到1米,参考数据:,,,)
22.图1是一种阅读支架,图2是其侧面示意图,托板、支撑杆可分别绕点B,D 转动,B 为的中点.研究发现,阅读最佳视觉角度是眼视线与水平面夹角为,小涵想要以此视角使用阅读支架.已知支撑杆长,其与桌面夹角,托板长,点E 是小涵眼睛的位置,是小涵阅读书本的视线,于点F,小涵眼睛与桌面的距离为.请你计算的长度.
(结果精确到,参考数据: )
23.如图,点O为矩形ABCD的对角线AC上一点,以OA为半径的⊙O交AD于点E,交AC于点F,且.
(1)求证:直线CE是⊙O的切线;
(2)若,,求⊙O的半径.
24.如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE,
(1)求证:△ABE≌△DFA.
(2)如果AD=10,AB=6,求sin∠EDF的值.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B A D D B C B B
题号 11 12
答案 A B
1.D
【分析】根据矩形的判断定理、相似三角形的性质、反比例函数的性质、坡度的定义及特殊的三角函数值解答即可.
【详解】对角线相等的平行四边形是矩形,故A错误;
相似三角形的面积比等于相似比的平方,故B错误;
在反比例函数图像上,在每个象限内,随的增大而增大,故C错误;
若一个斜坡的坡度为,则tan坡角= ,该斜坡的坡角为,故D正确.
故选:D
【点睛】本题考查的是矩形的判断定理、相似三角形的性质、反比例函数的性质、坡度的定义及特殊的三角函数值,熟练的掌握各图形及函数的性质是关键.
2.C
【详解】过点E作EM⊥AB于点M,
∵斜坡CD的坡度(或坡比)i=1:2.4,BC=CD=13米,
∴设DG=x,则CG=2.4x.
在Rt△CDG中,∵,即 解得x=5,
∴DG=5米,CG=12米,
∴EG=5+0.5=5.5米,BG=13+12=25米,
∵EM⊥AB,AB⊥BG,EG⊥BG,
∴四边形EGBM是矩形,
∴EM=BG=25米,BM=EG=5.5米,
在Rt△AEM中,
∵
∴米,
∴AB=AM+BM=22.5+5.5=28米.
故选C.
3.B
【分析】根据题意,可得Rt△ABC,同时可知AC与∠ACB.根据三角函数的定义解答.
【详解】根据题意,在Rt△ABC,有AC=a,∠ACB=50°,且tan50°=,
则AB=AC×tan50°=a tan50°,
故选B.
【点睛】本题考查了解直角三角形的应用,要熟练掌握三角函数的定义.
4.A
【分析】利用所给的角的三角函数用AB表示出BD,CB;根据BC﹣DB=CD即可求出建筑物AB的高度.
【详解】解:∵在Rt△ABC中,∠ACB=30°,
∴tan∠ACB=tan30°=,
∴BC==AB,
∵在Rt△ABD中,∠ADB=45°,
∴tan∠ADB=tan45°=,
∴BD==AB.
∵CD=BC﹣BD=16,
∴AB﹣AB=16,
解得:AB=8(+1)m.
故选:A.
【点睛】本题考查了仰角问题,解决此类问题的关键是正确的将仰角转化为直角三角形的内角并选择正确的边角关系解直角三角形.
5.D
【分析】分两种情况,根据圆周角定理和圆内接四边形的性质求解即可.
【详解】解:情形一、如图,作直径,连接DB,点A在上,
∵为直径,半径为2,
∴CD=4,,
在中,∵,CD=4
∴,
∴,
∴.
情形二:如图,作直径,连接DB,点A在劣弧上,
∵为直径,半径为2,
∴CD=4,,
在中,∵,CD=4
∴,
∴,
∵四边形ABDC是圆的内接四边形,
∴
∴
∴琪琪的说法正确,还有一个答案为120°
故选:D
【点睛】本题考查了圆周角定理,圆内接四边形的性质以及解直角三角形等知识点,能综合运用知识点进行推理是解此题的关键.
6.D
【分析】先求出120°的补角为60°,然后再把60°放在直角三角形中,所以过点C作CD⊥AB,交BA的延长线于点D,在Rt△ACD中可求出AD与CD的长,最后在Rt△BDC中利用勾股定理求出BC即可解答.
【详解】解:过点C作CD⊥AB,交BA的延长线于点D,
∵∠BAC=120°,
∴∠CAD=180°-∠BAC=60°,
在Rt△ACD中,AC=2,
∴AD=ACcos60°=2×=1,
CD=ACsin60°=2×=,
∵AB=4,
∴BD=AB+AD=4+1=5,
∴tanB=,
故选:D.
【点睛】本题考查了解直角三角形,勾股定理,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
7.B
【分析】根据题意可求出点B坐标,设点C的坐标为(3,t),根据CA=CB,利用两点间的距离公式,列出关系式,求出t的值,即可求出点C的坐标.
【详解】解:∵点A(-2,0),直线交轴于点,,
∴,
∴,
∴点B的坐标为(0,),
设点C的坐标为(3,t),
∵CA=CB,
∴,
解得,
∴点C的坐标为.
故选:B.
【点睛】本题主要考查坐标与图形性质,熟练掌握直角三角形的性质、两点间的距离公式是解答此题的关键.
8.C
【分析】根据题意和函数图象可以写出各段对应的函数解析式,从而可以判断哪个选项中的图象符合题意,本题得以解决.
【详解】解:当时,,即S与t是二次函数关系,有最小值,开口向上,
当时,,即S与t是二次函数关系,开口向下,
由上可得,选项C符合题意,
故选C.
【点睛】考查动点问题的函数过图象,解答本题的关键是明确题意,利用数形结合的思想解答.
9.B
【分析】
本题考查了解直角三角形的应用-坡度坡角问题,掌握坡度坡角的概念,熟记锐角三角函数的定义是解题的关键.
根据正弦的定义进行解答即可.
【详解】
解:在中,,,,
∵,
∴,
故选:B.
10.B
【分析】根据折叠的性质得出,设,则,在中,根据勾股定理得出,列出方程求出x的值,最后根据正切的定义,即可解答.
【详解】解:∵沿折叠得到,
∴,
设,则,
在中,根据勾股定理可得:,
即,解得:,
∴,
故选:B.
【点睛】本题主要考查了折叠的性质,勾股定理,正切的定义,解题的关键是掌握折叠前后对应边相等.
11.A
【分析】本题考查了解直角三角形,在直角三角形中,由已知元素求未知元素的过程就是解直角三角形,也考查了等腰直角三角形的性质,作于,由,得,根据等腰直角三角形的性质得到 ,设则,,在中,利用的正切得到,然后由可计算出 ,再利用 ,进行计算即可,解题的关键是添加辅助线构造直角三角形,再利用三角函数求边长.
【详解】作于,如图,
∵,
∴,
∵,
∴,
∴,是等腰直角三角形,
∴,
在中,设,则,
则,
在中,,
∴,
∴,解得:,
∴,
故选:.
12.B
【分析】
由菱形的性质可为直角三角形,根据锐角三角函数值得到、,求、的长,由菱形的面积公式可求解.
【详解】
解:∵四边形是菱形,
,,
为直角三角形,
点为的中点,,
,
,
,
,
,
,
,
∴菱形的面积=
故选:B.
【点睛】本题考查了菱形的性质,锐角三角函数,熟练运用菱形面积公式是本题的关键.
13.120°/120度
【分析】根据特殊角的三角函数值求出∠A的度数,然后根据三角形的内角和求解即可.
【详解】解:∵cosA=,
∴∠A=30 ,
∵∠B=30°,
∴∠C=180 -∠A-∠B=120 .
故答案为120°.
【点睛】此题主要考查了特殊角的三角函数值的应用,关键是熟记三角函数值和角的度数之间的关系,比较简单.
14.
【详解】试题分析:∵∠AED与∠ABC都对,
∴∠AED=∠ABC,
在Rt△ABC中,AB=2,AC=1,
根据勾股定理得:BC=,
则cos∠AED=cos∠ABC= =.
考点:1.圆周角定理;2.勾股定理;3.锐角三角函数的定义.
15.或4
【分析】由正方形的性质得出BC=AB=AD=CD=DE+EC,∠BAD=∠C=∠D=90°;分两种情况:①当点F在AD边上时,求出tan∠ABF即可;②当点F在CD边上时,求出tan∠ABF.
【详解】解:∵四边形ABCD是正方形,
∴AB=AD=CD=DE+EC,∠BAD=∠C=∠D=90°,,
∵,
∴设,则,BC=AB=AD=CD=4x;
分两种情况:
①当点F在AD边上时,如图所示:
在和中,
,
,
,
;
②当点F在CD边上时,如图所示:
在和中,
,
,
,
,
,
;
故答案为:或.
【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,正切的定义,熟练掌握正方形的性质,正切的定义是解题的关键.
16.20
【分析】根据坡度是坡面的铅直高度和水平宽度的比,再根据勾股定理即可求出该大坝迎水坡AB的长度.
【详解】解:如图,过点B作BC垂直于水平面于点C,可知BC=16米,
∵BC:AC=1:0.75,
∴16:AC=1:0.75,
∴AC=12(米),
∴AB==20(米),
答:该大坝迎水坡AB的长度为20米.
故答案为:20.
【点睛】本题考查了解直角三角形的应用-坡度坡角问题,解决本题的关键是掌握坡度坡角定义.
17.或
【分析】本题考查了矩形的性质,勾股定理,折叠性质,解答时分店E落在横对称轴上和纵对称轴上,两种情况计算即可,采用分类讨论的思想是解此题的关键.
【详解】如图当点E落在对称上时,
∵ 矩形中,,沿折叠得对应,
∴,,,
,
∴,,,
设,则,
∴,
解得;
如图当点E落在对称上时,设的交点为Q,
∵ 矩形中,,沿折叠得对应,
∴,,
,
∴,
∴,
∴,
∴是等边三角形,
∴,,,
∴,
∴,
故答案为:或.
18.(1)1
(2)
【分析】本题主要考查了锐角三角函数的混合运算:
(1)先把特殊角锐角三角函数值代入,再计算,即可求解;
(2)先把特殊角锐角三角函数值代入,再计算,即可求解.
【详解】(1)解:
(2)解:
19.(1)见解析;
(2)见解析;
(3)见解析
【分析】(1)利用网格特点,构造△ABC是以AB为底的等腰直角三角形即可;
(2)根据等腰三角形的定义画出即可;
(3)由于tan∠MNP=,则在含∠MNP的直角三角形中,满足对边与邻边之比为1:2即可.
【详解】(1)解:如图1,△ABC为所作:
∵AC=,,,
∴,,
∴△ABC是以AB为斜边的等腰直角三角形,
∴∠CAB=45°,
即△CAB满足要求;
(2)如图2所示:
由勾股定理得,,
∴DE=EF=5,
∴△DEF是等腰三角形,
∵,
∴△DEF满足要求;
(3)如图3所示:
∵,,,
∴
∴△MNP是以MN为斜边的直角三角形,
∴,
即作图符合要求.
【点睛】本题考查了勾股定理及其逆定理、锐角三角比、等腰直角三角形的判定和性质等知识,熟练掌握勾股定理及其逆定理是解题的关键.
20.(1)①(或);②;③
(2)旗杆的高度约为
【分析】(1)本题考查相似三角形的性质与判定,根据题意证明,再利用相似三角形对应边成比例,建立等式求解,即可解题.
(2)本题考查解直角三角形,根据题意得出、,利用,求得,再根据,即可解题.
【详解】(1)解:由测量知,,,,
法线,,
,
,
,
,即,
,
故旗杆的高度为.
故答案为:(或);;;
(2)解:由题知,,,,,
,,
,
,即,解得,
,
旗杆的高度约为.
21.28米
【分析】本题考查了解直角三角形的应用的仰俯角问题,熟练掌握锐角三角函数与边的关系是解题的关键;
过点D分别作于点E,于点F.得四边形是矩形,
在中,根据坡比为,求出(米),(米),,在中,,求出,即可得出塔的高度.
【详解】解:过点D分别作于点E,于点F.
∴四边形是矩形.
∴,.
在中,
∵,
∴,.
∴(米),(米).
∴(米).
在中,,
∴(米).
∴(米).
答:高贤寿圣寺塔AB的高度约为28米.
22.
【分析】本题考查解直角三角形的实际应用,矩形的判定和性质等知识,过点B作,垂足分别为,即得出四边形是矩形,;结合题意,,从而求得,进面可求,最的根据求解即可.
【详解】解:如图,过点B作,垂足分别为.
,
四边形是矩形,
,
在中,,
,
,
,
,
,
在中,,
,
,
.
23.(1)见解析;(2)
【分析】(1)根据矩形的性质及,证明即可;
(2)过点O作于点H,由(1)的结论及求出,继而在中用勾股定理即可求得半径.
【详解】(1)证明:连接OE,
∵矩形ABCD中,,
,
∴,,
,,
∵,
∴,
∴,
∵,
∴,∴,
又∵OE为⊙O半径CE过点E,∴直线CE是⊙O的切线.
(2)过点O作于点H,
则,
∵,,
∴,
∴,
∴,
∴,
在中,
.
【点睛】本题考查了矩形的性质,圆的切线的判定与性质,锐角三角函数,勾股定理,正确的作出辅助线是解题的关键.
24.(1)证明见解析;(2).
【分析】(1)根据矩形的对边平行且相等得到AD=BC=AE,∠DAF=∠AEB.再结合一对直角相等即可证明三角形全等;
(2)根据全等三角形的对应边相等以及勾股定理,可以求得DF,EF的长;再根据勾股定理求得DE的长,运用三角函数定义求解.
【详解】(1)在矩形中,,
.
,
,.
.
(2)由(1)知.
.
在直角中,,
.
在Rt中,,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
