第二十九章投影与三视图同步练习(含解析)
文档属性
| 名称 | 第二十九章投影与三视图同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 943.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 20:40:25 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十九章投影与三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
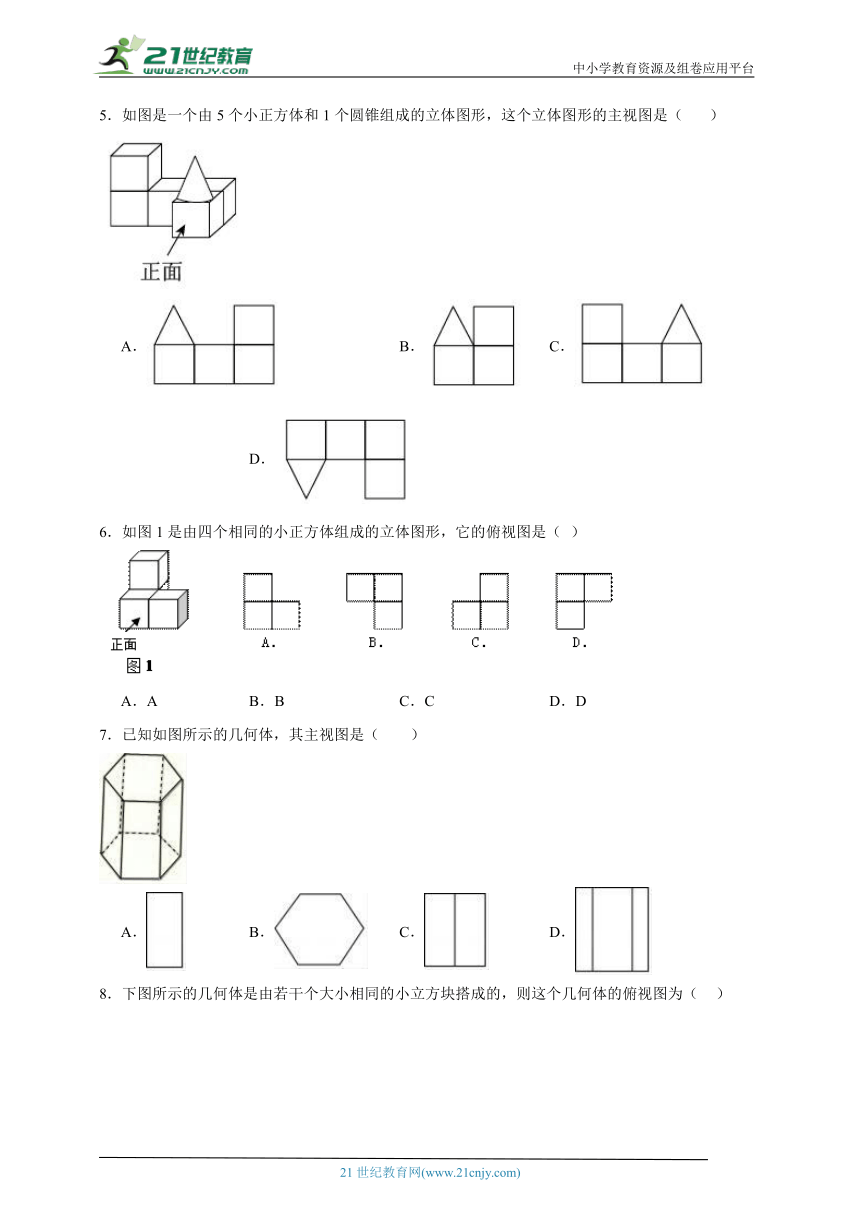
1.两个完全相同的长方体,按如图方式摆放,其主视图为( )
A. B.
C. D.
2.如图,图1是一个底面为正方形的直棱柱;现将图1切割成图2的几何体,则图2的俯视图是( )
A. B. C. D.
3.下列图形中,三视图都相同的是( )
A.圆柱 B.球 C.三棱锥 D.五棱柱
4.如图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),可判断形成该影子的光线为( )
A.该影子实际不可能存在 B.可能是太阳光线也可能是灯光光线
C.太阳光线 D.灯光光线
5.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
6.如图1是由四个相同的小正方体组成的立体图形,它的俯视图是( )
A.A B.B C.C D.D
7.已知如图所示的几何体,其主视图是( )
A. B. C. D.
8.下图所示的几何体是由若干个大小相同的小立方块搭成的,则这个几何体的俯视图为( )
A. B. C. D.
9.一个几何体的主视图和左视图都是矩形,俯视图是圆,则这个几何体是( )
A.三棱柱 B.圆柱 C.三棱柱 D.圆锥
10.如图是由五个相同的小正方体搭成的几何体,它的右视图是( )
A.
B.
C.
D.
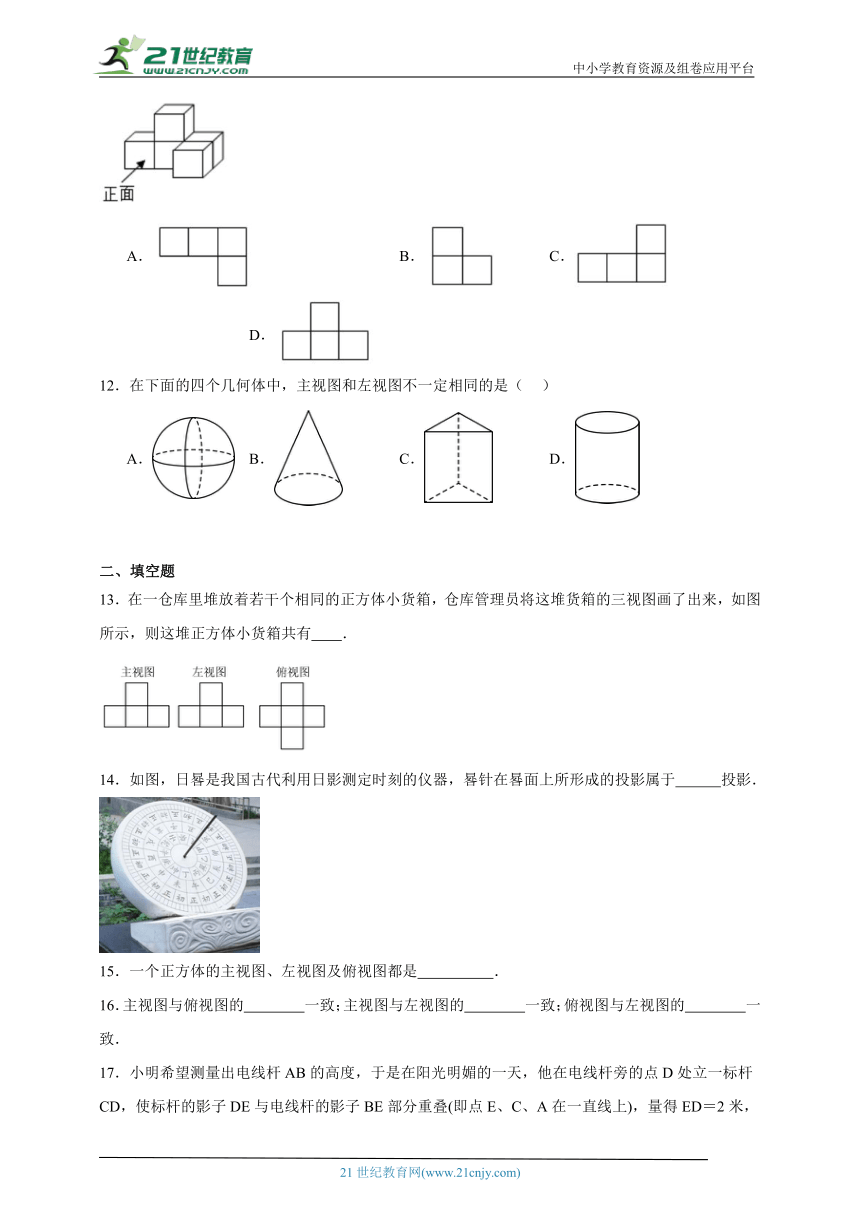
11.如图是由5个大小相同的小正方体搭成的几何体,它的俯视图是( )
A. B. C. D.
12.在下面的四个几何体中,主视图和左视图不一定相同的是( )
A. B. C. D.
二、填空题
13.在一仓库里堆放着若干个相同的正方体小货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体小货箱共有 .
14.如图,日晷是我国古代利用日影测定时刻的仪器,晷针在晷面上所形成的投影属于 投影.
15.一个正方体的主视图、左视图及俯视图都是 .
16.主视图与俯视图的 一致;主视图与左视图的 一致;俯视图与左视图的 一致.
17.小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米,则电线杆AB长为
三、解答题
18.某糖果厂想要为儿童设计一种新型的装糖果的不倒翁,请你根据包装厂设计好的三视图(如图)的尺寸计算其体积.(球的体积公式:其中r为球的半径)
19.分别画出下图中的物体的三视图:
20.如图,路灯下竖立的一根木杆(用线段表示)的影子,小明(用线段表示)的影子是.
(1)请在图中画出路灯的位置(用点P表示);
(2)若此路灯距地面高8米,小红的身高1.6米在距离灯的底部左侧6米N处,此时小红沿方向向左直走,求当小红的影长是5米时,她所走的路程.
21.新学期,小华和小明被选为升旗手,为了更好地完成升旗任务,他想测量学校旗杆的高度. 方案如下:
课题 测量校园旗杆的高度
测量工具 侧倾器、皮尺
测量图例
测量方法 在阳光下,小华站在旗杆影子的顶端处,此刻量出小华的影长;然后,在旗杆落在地面的影子上的点处,安装测倾器,测出旗杆顶端的仰角.
测量数据 小华的影长,小华身高,顶端的仰角为,侧倾器高,,旗台高.
说明 点、、、在同一水平直线上,点、、在同一条直线上,、、均垂直于参考数据:.
请你根据上述信息,求旗杆的高度
22.如图,王琳同学在晚上由路灯走向路灯,当他行到处时发现,他在路灯下的影长为米,且恰好位于路灯的正下方,接着他又走了米到处,此时他在路灯下的影子恰好位于路灯的正下方(已知王琳身高米,路灯高米)
(1)标出王琳站在处在路灯下的影子;
(2)计算王琳站在处在路灯下的影长;
(3)计算路灯的高度.
23.如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
24.求证:一个人在两个高度相同的路灯之间行走,他前后的两个影子的长度之和是一个定值.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D C A D B B B
题号 11 12
答案 A C
1.B
【分析】根据从正面看到的几何体的形状选择即可.
【详解】从正面看到的几何体的形状如图,
故选:B
【点睛】此题考查了简单组合体的三视图,根据几何体正确判断三视图是解题关键,注意:几何体中实际存在但看不到的轮廓线要用虚线画出来.
2.C
【分析】俯视图是从物体上面看到的图形,应把所看到的所有棱都表示在所得图形中.
本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.
【详解】解:从上面看,图2的俯视图是正方形,有一条对角线.
故选:C.
3.B
【分析】根据三视图的基本知识,分析各个几何体的三视图然后可解答.
【详解】解:圆柱,球,三棱锥,五棱柱中,三视图都相同的几何体只有球,在任意方向上的视图都是圆.
故选:B.
【点睛】本题难度一般,主要考查的是三视图的基本知识.解题时也应具有一定的生活经验.
4.D
【分析】根据平行投影和中心投影的特点分析判断即可.
【详解】解:若影子是由太阳光照射形成的,则两条直线一定平行;若影子是由灯光照射形成的,则两条直线一定相交.据此可判断形成该影子的光线为灯光光线.
故选:D.
【点睛】本题主要考查了平行投影和中心投影的特点及规律,解题关键是准确区分平行投影和中心投影.
5.C
【分析】直接根据从正面看到的图形即可求解.
【详解】解:从正面看到的图形为 ,
故选:C
【点睛】本题考查了立体图形的三视图,理解三视图的概念是解题的关键.
6.A
【详解】试题解析:从上边看第一层是一个小正方形,第二层是一个小正方形,右边一个小正方形,
故选A.
7.D
【分析】主视图是三视图中的一种,从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状,据此观察所给的几何体即可得出答案.
【详解】解:从物体正面看,看到的是一个中间有两条竖线的矩形,观察选项,只有D选项符合,
故选:D.
【点睛】本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图,关键是掌握主视图所看的位置.
8.B
【分析】本题考查三视图,根据从上向下看得到的图形为俯视图,进行判断即可.
【详解】解:这个几何体的俯视图为
故选B.
9.B
【详解】试题分析:根据几何体的主视图和左视图都是矩形,得出几何体是柱体,再根据俯视图为圆,易判断该几何体是一个圆柱.
解:一个几何体的主视图和左视图都是矩形,俯视图是圆,符合这个条件的几何体只有圆柱,因此这个几何体是圆柱体.
故选B.
考点:由三视图判断几何体.
10.B
【分析】找到从右面看所得到的图形即可.
【详解】从右面看可得到从左往右两列正方形的个数依次为:1,2,
故选B.
【点睛】本题考查了几何体的视图知识,右视图是从物体的右面看得到的视图.
11.A
【分析】根据从上面看得到的图形是俯视图,可得答案.
【详解】解:从上面看第一列是一个小正方形,第二列是一个小正方形,第三列是两个小正方形,
故选:A.
【点睛】本题考查了简单组合体的三视图,从上面看得到的图形是俯视图.
12.C
【分析】此题主要考查了简单几何体的三视图分别找出每个立体图形的左视图和主视图即可得到答案.
【详解】解:A、球体主视图和左视图都是相同的圆,故此选项不合题意;
B、圆锥主视图和左视图都是相同的三角形,故此选项不合题意;
C、三棱柱主视图和左视图都是长方形,但宽不同,故此选项符合题意;
D、圆柱的主视图和左视图都是相同的长方形,故此选项不合题意;
故选:C.
13.6个
【分析】根据俯视图,以及主视图与左视图,确定出小货箱的数目即可.
【详解】解:根据三视图可得,第一层为5个,第二层为1个(在中间):这堆正方体小货箱共有6箱,
故答案为6
【点睛】此题考查了由三视图判断几何体,熟练掌握三视图的性质是解本题的关键.
14.平行
【分析】根据太阳光是平行光线可以判定晷针在晷面上所形成的投影属于平行投影.
【详解】解:因为太阳光属于平行光线,而日晷利用日影测定时刻,所以晷针在晷面上所形成的投影属于平行投影.
故答案为:平行.
【点睛】本题考查的是平行投影的概念:如果把中心投影法的投射中心移至无穷远处,则各投射线成为相互平行的直线,这种投影法称为平行投影法.
15.正方形
【分析】根据正方体的特征即可得到结果.
【详解】解:一个正方体的主视图、左视图及俯视图都是正方形.
故答案为:正方形
【点睛】本题考查的是正方体的三视图,解答本题的关键是熟记正方体的三视图均是正方形.
16. 长 高 宽
【分析】根据三视图的特征,主视图与俯视图长对正;主视图与左视图高平齐;俯视图与左视图的宽相等进行填空即可.
【详解】∵主视图与俯视图长对正;主视图与左视图高平齐;俯视图与左视图的宽相等,
∴主视图与俯视图的长一致;主视图与左视图的高一致;俯视图与左视图的宽一致.
故答案是:长、高、宽.
【点睛】考查了简单几何体的三视图,掌握三视图的定义是关键.注意所有的看到的棱都应表现在三视图中.
17.4.5
【分析】根据题意求出△ECD∽△EAB,利用相似三角形的对应边成比例即可解答.
【详解】∵CD∥AB,
∴△ECD∽△EAB,
∴ED:EB=CD:AB,
∴2:6=1.5:AB,
∴AB=4.5米.
答:电线杆AB长为4.5米.
故答案为4.5.
【点睛】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出电线杆AB长.
18.不倒翁的体积为:
【分析】由已知中的三视图,我们可以判断出该几何体的形状为:下部是底面半径为的半球,上部为底面半径为,母线长13cm的圆锥组成的组成体,代入圆锥体积公式和球的体积公式,即可得到答案.
【详解】解:此几何体是圆锥和半球的组合体,
如图所示:
∵,,
∴,
∴,
∴上面圆锥的体积为:,
下面半球体积为:
∴该几何体的容积为:.
【点睛】此题主要考查了由三视图判断几何体、几何体体积的计算,正确得出几何体的组成是解题关键.
19.见解析.
【分析】主视图、俯视图、左视图,分别是从物体正面、上面、左面看,所得到的图形.依此作出图中两个物体的三视图.
【详解】主视图: 左视图: 俯视图:
【点睛】本题考查三视图的画法;用到的知识点为:三视图分别是从物体正面,左面,上面看得到的平面图形;注意实际存在又没有被其他棱所挡,在所在方向看不到的棱应用虚线表示.
20.(1)见解析
(2)14米
【分析】本题主要考查了相似三角形的应用:
(1)连接,并延长交于点P,即可;
(2)过点P作于点H,设当小红的影长是5米时,到达点, 表示小红的身高,表示此时的影长,则米,米,,可得,从而得到米,即可求解.
【详解】(1)解:如图,点P即为所求;
(2)解:如图,过点P作于点H,设当小红的影长是5米时,到达点, 表示小红的身高,表示此时的影长,则米,米,,
∴,
∴,
∴,
∴米,
∴米,
即当小红的影长是5米时,她所走的路程14米.
21.旗杆的高度为
【分析】本题考查测高,涉及三角函数测高、利用太阳光测高、解直角三角形、相似三角形的判定与性质等知识,设,在中,解直角三角形得到,从而求出相关线段长,再根据,由相似列式求解即可得到答案,掌握测高题型及解法是解决问题的关键.
【详解】解:过作,如图所示:
设,则,
,
,
在中,,解得,
,即,
在太阳光下,,则,
,解得,
答:旗杆的高度为.
22.(1)线段
(2)米
(3)米
【分析】本题考查相似三角形的应用,
(1)影子为光线与物高相交得到的阴影部分;
(2)证明,利用对应边成比例可得长;
(3)证明,利用对应边成比例可得长,也就是路灯的高度;
解题的关键是掌握:两角对应相等的两三角形相似;相似三角形的对应边成比例.
【详解】(1)解:线段为王琳在站在处路灯下的影子;
(2)根据题意知:,,,,,,,
∴,,
∵,
∴,
∴,
∴,
解得:,
答:王琳站在处在路灯下的影长为米;
(3)由(2)知:,
∵,
∴,
∴,
∴,
解得:,
答:路灯的高度为米.
23.(1)AC的投影是AD,CD的投影是点D,BC的投影是BD;(2)证明见解析.
【详解】试题分析:(1)在平行投影中,投影线垂直于投影面产生的投影叫做正投影,根据正投影的定义求解即可;
(2)①,结合两角对应相等的两三角形相似,可得△BCD∽△BAC,根据相似三角形对应边成比例可证明结论;
②同理可证△ACD∽△CBD,根据相似三角形对应边成比例可证明结论成立.
试题解析:
解:(1)∵CD⊥AB,
而平行光线垂直AB,
∴AC的投影是AD,CD的投影是点D,BC的投影为BD;
(2)①∵∠ACB=90°,CD⊥AB于D,
∴∠ACB=∠CDB=90°.
∵∠B=∠B,
∴△BCD∽△BAC,
∴,
∴BC2=BD AB;
②同理可得:△ACD∽△CBD,
∴,
∴CD2=AD BD.
点睛:本题考查了正投影的定义和相似三角形的判定与性质,熟记正投影的定义是解决(1)的关键,结合图形得出相似三角形是解决(2)的关键.
24.见解析
【分析】根据题意作出图象,利用相似三角形的性质说明即可.
【详解】解:如图所示,CD、EF为路灯高度,AB为该人高度,BM、BN为该人前后的两个影子.
∵AB∥CD,
∴△ABM∽△CDM
∴,
∴,
即 MB=.
同理BN=.
∴MB+BN==常数(定值).
【点睛】本题考查了相似三角形的应用,正确的根据题意作出图形并利用相似三角形的判定和性质推理论证是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十九章投影与三视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.两个完全相同的长方体,按如图方式摆放,其主视图为( )
A. B.
C. D.
2.如图,图1是一个底面为正方形的直棱柱;现将图1切割成图2的几何体,则图2的俯视图是( )
A. B. C. D.
3.下列图形中,三视图都相同的是( )
A.圆柱 B.球 C.三棱锥 D.五棱柱
4.如图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),可判断形成该影子的光线为( )
A.该影子实际不可能存在 B.可能是太阳光线也可能是灯光光线
C.太阳光线 D.灯光光线
5.如图是一个由5个小正方体和1个圆锥组成的立体图形,这个立体图形的主视图是( )
A. B. C. D.
6.如图1是由四个相同的小正方体组成的立体图形,它的俯视图是( )
A.A B.B C.C D.D
7.已知如图所示的几何体,其主视图是( )
A. B. C. D.
8.下图所示的几何体是由若干个大小相同的小立方块搭成的,则这个几何体的俯视图为( )
A. B. C. D.
9.一个几何体的主视图和左视图都是矩形,俯视图是圆,则这个几何体是( )
A.三棱柱 B.圆柱 C.三棱柱 D.圆锥
10.如图是由五个相同的小正方体搭成的几何体,它的右视图是( )
A.
B.
C.
D.
11.如图是由5个大小相同的小正方体搭成的几何体,它的俯视图是( )
A. B. C. D.
12.在下面的四个几何体中,主视图和左视图不一定相同的是( )
A. B. C. D.
二、填空题
13.在一仓库里堆放着若干个相同的正方体小货箱,仓库管理员将这堆货箱的三视图画了出来,如图所示,则这堆正方体小货箱共有 .
14.如图,日晷是我国古代利用日影测定时刻的仪器,晷针在晷面上所形成的投影属于 投影.
15.一个正方体的主视图、左视图及俯视图都是 .
16.主视图与俯视图的 一致;主视图与左视图的 一致;俯视图与左视图的 一致.
17.小明希望测量出电线杆AB的高度,于是在阳光明媚的一天,他在电线杆旁的点D处立一标杆CD,使标杆的影子DE与电线杆的影子BE部分重叠(即点E、C、A在一直线上),量得ED=2米,DB=4米,CD=1.5米,则电线杆AB长为
三、解答题
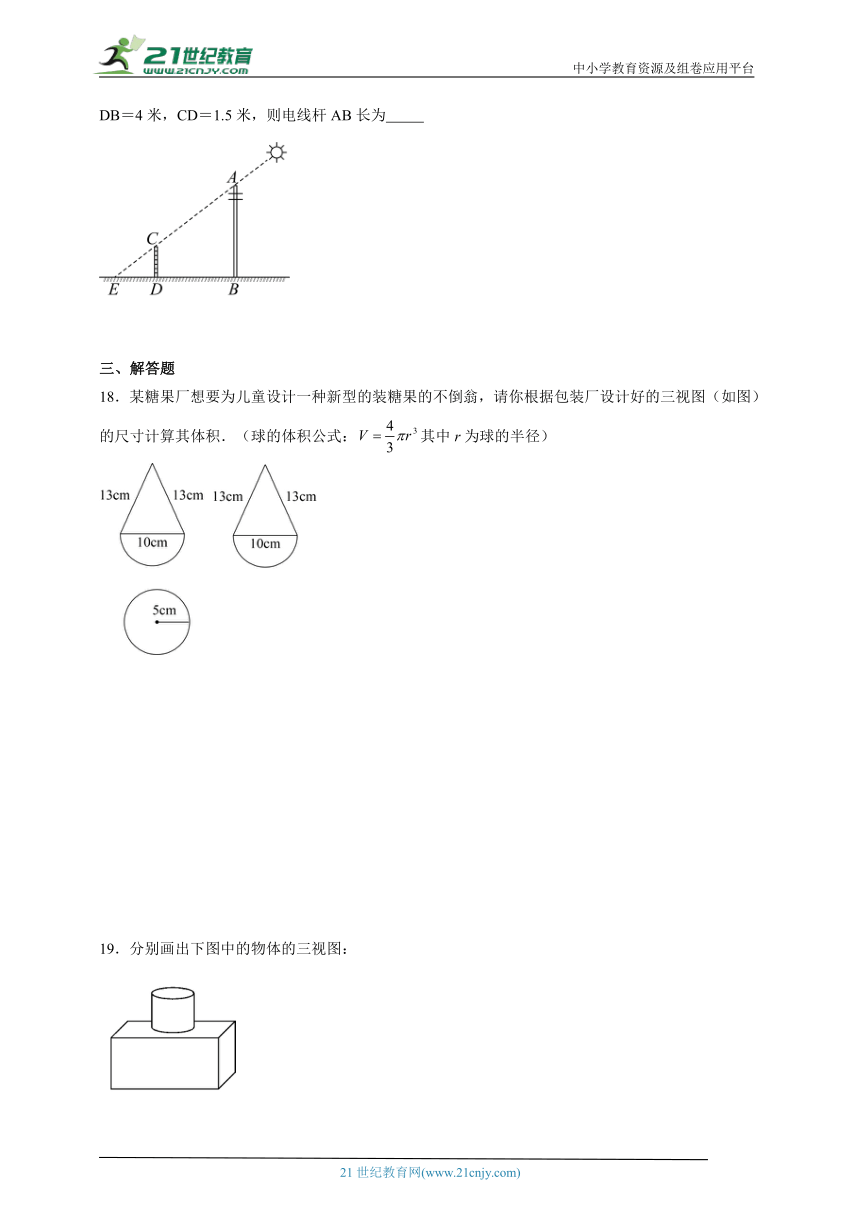
18.某糖果厂想要为儿童设计一种新型的装糖果的不倒翁,请你根据包装厂设计好的三视图(如图)的尺寸计算其体积.(球的体积公式:其中r为球的半径)
19.分别画出下图中的物体的三视图:
20.如图,路灯下竖立的一根木杆(用线段表示)的影子,小明(用线段表示)的影子是.
(1)请在图中画出路灯的位置(用点P表示);
(2)若此路灯距地面高8米,小红的身高1.6米在距离灯的底部左侧6米N处,此时小红沿方向向左直走,求当小红的影长是5米时,她所走的路程.
21.新学期,小华和小明被选为升旗手,为了更好地完成升旗任务,他想测量学校旗杆的高度. 方案如下:
课题 测量校园旗杆的高度
测量工具 侧倾器、皮尺
测量图例
测量方法 在阳光下,小华站在旗杆影子的顶端处,此刻量出小华的影长;然后,在旗杆落在地面的影子上的点处,安装测倾器,测出旗杆顶端的仰角.
测量数据 小华的影长,小华身高,顶端的仰角为,侧倾器高,,旗台高.
说明 点、、、在同一水平直线上,点、、在同一条直线上,、、均垂直于参考数据:.
请你根据上述信息,求旗杆的高度
22.如图,王琳同学在晚上由路灯走向路灯,当他行到处时发现,他在路灯下的影长为米,且恰好位于路灯的正下方,接着他又走了米到处,此时他在路灯下的影子恰好位于路灯的正下方(已知王琳身高米,路灯高米)
(1)标出王琳站在处在路灯下的影子;
(2)计算王琳站在处在路灯下的影长;
(3)计算路灯的高度.
23.如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
24.求证:一个人在两个高度相同的路灯之间行走,他前后的两个影子的长度之和是一个定值.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D C A D B B B
题号 11 12
答案 A C
1.B
【分析】根据从正面看到的几何体的形状选择即可.
【详解】从正面看到的几何体的形状如图,
故选:B
【点睛】此题考查了简单组合体的三视图,根据几何体正确判断三视图是解题关键,注意:几何体中实际存在但看不到的轮廓线要用虚线画出来.
2.C
【分析】俯视图是从物体上面看到的图形,应把所看到的所有棱都表示在所得图形中.
本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.
【详解】解:从上面看,图2的俯视图是正方形,有一条对角线.
故选:C.
3.B
【分析】根据三视图的基本知识,分析各个几何体的三视图然后可解答.
【详解】解:圆柱,球,三棱锥,五棱柱中,三视图都相同的几何体只有球,在任意方向上的视图都是圆.
故选:B.
【点睛】本题难度一般,主要考查的是三视图的基本知识.解题时也应具有一定的生活经验.
4.D
【分析】根据平行投影和中心投影的特点分析判断即可.
【详解】解:若影子是由太阳光照射形成的,则两条直线一定平行;若影子是由灯光照射形成的,则两条直线一定相交.据此可判断形成该影子的光线为灯光光线.
故选:D.
【点睛】本题主要考查了平行投影和中心投影的特点及规律,解题关键是准确区分平行投影和中心投影.
5.C
【分析】直接根据从正面看到的图形即可求解.
【详解】解:从正面看到的图形为 ,
故选:C
【点睛】本题考查了立体图形的三视图,理解三视图的概念是解题的关键.
6.A
【详解】试题解析:从上边看第一层是一个小正方形,第二层是一个小正方形,右边一个小正方形,
故选A.
7.D
【分析】主视图是三视图中的一种,从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状,据此观察所给的几何体即可得出答案.
【详解】解:从物体正面看,看到的是一个中间有两条竖线的矩形,观察选项,只有D选项符合,
故选:D.
【点睛】本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图,关键是掌握主视图所看的位置.
8.B
【分析】本题考查三视图,根据从上向下看得到的图形为俯视图,进行判断即可.
【详解】解:这个几何体的俯视图为
故选B.
9.B
【详解】试题分析:根据几何体的主视图和左视图都是矩形,得出几何体是柱体,再根据俯视图为圆,易判断该几何体是一个圆柱.
解:一个几何体的主视图和左视图都是矩形,俯视图是圆,符合这个条件的几何体只有圆柱,因此这个几何体是圆柱体.
故选B.
考点:由三视图判断几何体.
10.B
【分析】找到从右面看所得到的图形即可.
【详解】从右面看可得到从左往右两列正方形的个数依次为:1,2,
故选B.
【点睛】本题考查了几何体的视图知识,右视图是从物体的右面看得到的视图.
11.A
【分析】根据从上面看得到的图形是俯视图,可得答案.
【详解】解:从上面看第一列是一个小正方形,第二列是一个小正方形,第三列是两个小正方形,
故选:A.
【点睛】本题考查了简单组合体的三视图,从上面看得到的图形是俯视图.
12.C
【分析】此题主要考查了简单几何体的三视图分别找出每个立体图形的左视图和主视图即可得到答案.
【详解】解:A、球体主视图和左视图都是相同的圆,故此选项不合题意;
B、圆锥主视图和左视图都是相同的三角形,故此选项不合题意;
C、三棱柱主视图和左视图都是长方形,但宽不同,故此选项符合题意;
D、圆柱的主视图和左视图都是相同的长方形,故此选项不合题意;
故选:C.
13.6个
【分析】根据俯视图,以及主视图与左视图,确定出小货箱的数目即可.
【详解】解:根据三视图可得,第一层为5个,第二层为1个(在中间):这堆正方体小货箱共有6箱,
故答案为6
【点睛】此题考查了由三视图判断几何体,熟练掌握三视图的性质是解本题的关键.
14.平行
【分析】根据太阳光是平行光线可以判定晷针在晷面上所形成的投影属于平行投影.
【详解】解:因为太阳光属于平行光线,而日晷利用日影测定时刻,所以晷针在晷面上所形成的投影属于平行投影.
故答案为:平行.
【点睛】本题考查的是平行投影的概念:如果把中心投影法的投射中心移至无穷远处,则各投射线成为相互平行的直线,这种投影法称为平行投影法.
15.正方形
【分析】根据正方体的特征即可得到结果.
【详解】解:一个正方体的主视图、左视图及俯视图都是正方形.
故答案为:正方形
【点睛】本题考查的是正方体的三视图,解答本题的关键是熟记正方体的三视图均是正方形.
16. 长 高 宽
【分析】根据三视图的特征,主视图与俯视图长对正;主视图与左视图高平齐;俯视图与左视图的宽相等进行填空即可.
【详解】∵主视图与俯视图长对正;主视图与左视图高平齐;俯视图与左视图的宽相等,
∴主视图与俯视图的长一致;主视图与左视图的高一致;俯视图与左视图的宽一致.
故答案是:长、高、宽.
【点睛】考查了简单几何体的三视图,掌握三视图的定义是关键.注意所有的看到的棱都应表现在三视图中.
17.4.5
【分析】根据题意求出△ECD∽△EAB,利用相似三角形的对应边成比例即可解答.
【详解】∵CD∥AB,
∴△ECD∽△EAB,
∴ED:EB=CD:AB,
∴2:6=1.5:AB,
∴AB=4.5米.
答:电线杆AB长为4.5米.
故答案为4.5.
【点睛】本题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程即可求出电线杆AB长.
18.不倒翁的体积为:
【分析】由已知中的三视图,我们可以判断出该几何体的形状为:下部是底面半径为的半球,上部为底面半径为,母线长13cm的圆锥组成的组成体,代入圆锥体积公式和球的体积公式,即可得到答案.
【详解】解:此几何体是圆锥和半球的组合体,
如图所示:
∵,,
∴,
∴,
∴上面圆锥的体积为:,
下面半球体积为:
∴该几何体的容积为:.
【点睛】此题主要考查了由三视图判断几何体、几何体体积的计算,正确得出几何体的组成是解题关键.
19.见解析.
【分析】主视图、俯视图、左视图,分别是从物体正面、上面、左面看,所得到的图形.依此作出图中两个物体的三视图.
【详解】主视图: 左视图: 俯视图:
【点睛】本题考查三视图的画法;用到的知识点为:三视图分别是从物体正面,左面,上面看得到的平面图形;注意实际存在又没有被其他棱所挡,在所在方向看不到的棱应用虚线表示.
20.(1)见解析
(2)14米
【分析】本题主要考查了相似三角形的应用:
(1)连接,并延长交于点P,即可;
(2)过点P作于点H,设当小红的影长是5米时,到达点, 表示小红的身高,表示此时的影长,则米,米,,可得,从而得到米,即可求解.
【详解】(1)解:如图,点P即为所求;
(2)解:如图,过点P作于点H,设当小红的影长是5米时,到达点, 表示小红的身高,表示此时的影长,则米,米,,
∴,
∴,
∴,
∴米,
∴米,
即当小红的影长是5米时,她所走的路程14米.
21.旗杆的高度为
【分析】本题考查测高,涉及三角函数测高、利用太阳光测高、解直角三角形、相似三角形的判定与性质等知识,设,在中,解直角三角形得到,从而求出相关线段长,再根据,由相似列式求解即可得到答案,掌握测高题型及解法是解决问题的关键.
【详解】解:过作,如图所示:
设,则,
,
,
在中,,解得,
,即,
在太阳光下,,则,
,解得,
答:旗杆的高度为.
22.(1)线段
(2)米
(3)米
【分析】本题考查相似三角形的应用,
(1)影子为光线与物高相交得到的阴影部分;
(2)证明,利用对应边成比例可得长;
(3)证明,利用对应边成比例可得长,也就是路灯的高度;
解题的关键是掌握:两角对应相等的两三角形相似;相似三角形的对应边成比例.
【详解】(1)解:线段为王琳在站在处路灯下的影子;
(2)根据题意知:,,,,,,,
∴,,
∵,
∴,
∴,
∴,
解得:,
答:王琳站在处在路灯下的影长为米;
(3)由(2)知:,
∵,
∴,
∴,
∴,
解得:,
答:路灯的高度为米.
23.(1)AC的投影是AD,CD的投影是点D,BC的投影是BD;(2)证明见解析.
【详解】试题分析:(1)在平行投影中,投影线垂直于投影面产生的投影叫做正投影,根据正投影的定义求解即可;
(2)①,结合两角对应相等的两三角形相似,可得△BCD∽△BAC,根据相似三角形对应边成比例可证明结论;
②同理可证△ACD∽△CBD,根据相似三角形对应边成比例可证明结论成立.
试题解析:
解:(1)∵CD⊥AB,
而平行光线垂直AB,
∴AC的投影是AD,CD的投影是点D,BC的投影为BD;
(2)①∵∠ACB=90°,CD⊥AB于D,
∴∠ACB=∠CDB=90°.
∵∠B=∠B,
∴△BCD∽△BAC,
∴,
∴BC2=BD AB;
②同理可得:△ACD∽△CBD,
∴,
∴CD2=AD BD.
点睛:本题考查了正投影的定义和相似三角形的判定与性质,熟记正投影的定义是解决(1)的关键,结合图形得出相似三角形是解决(2)的关键.
24.见解析
【分析】根据题意作出图象,利用相似三角形的性质说明即可.
【详解】解:如图所示,CD、EF为路灯高度,AB为该人高度,BM、BN为该人前后的两个影子.
∵AB∥CD,
∴△ABM∽△CDM
∴,
∴,
即 MB=.
同理BN=.
∴MB+BN==常数(定值).
【点睛】本题考查了相似三角形的应用,正确的根据题意作出图形并利用相似三角形的判定和性质推理论证是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
