第二十六章 反比例函数同步练习(含解析)
文档属性
| 名称 | 第二十六章 反比例函数同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 20:43:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
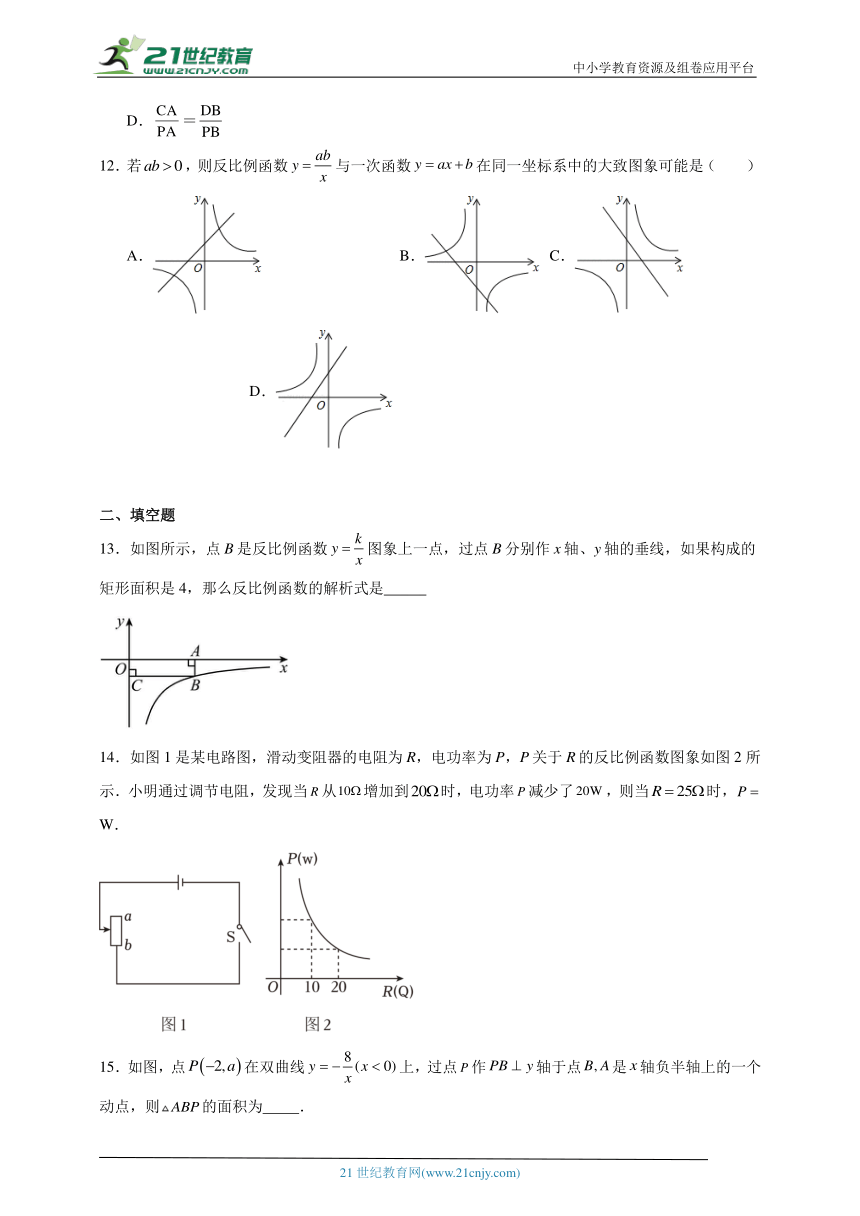
第二十六章反比例函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.反比例函数图象上有三个点,其中,则的大小关系是 ( )
A. B.
C. D.
2.对于反比例函数,下列说法正确的是( )
A.当时,y随x增大而增大 B.图象经过点
C.图象位于第一、三象限 D.当时,
3.若反比例函数的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )
A.-3 B.-1 C.0 D.3
4.如图,已知点,,C是y轴上位于点B上方的一点,AD平分,BE平分,直线BE交AD于点D.若反比例函数的图像经过点D,则k的值是( )
A. B. C. D.
5.函数与图象的一个交点的横、纵坐标分别为a、b,则的值为( )
A. B. C.3 D.
6.若正比例函数y=kx(k≠0)与反比例函数y=(a≠0)的图象有两个交点,其中一个交点的坐标为(-3,-2),则另一个交点的坐标为( )
A.(2,3) B.(3,-2) C.(-2,3) D.(3,2)
7.反比例函数的图象经过点,则该反比例函数的表达式是( )
A. B. C. D.
8.已知反比例函数y=的图象在一、三象限,那么直线y=kx﹣k不经过第( )象限.
A.一 B.二 C.三 D.四
9.在同一平面直角坐标系中,函数与函数的图象可能是( )
A. B. C. D.
10.若点均为反比例函数(m为常数)图象上的两点,当时,,则m的取值范围是( )
A. B. C. D.任意实数
11.两个反比例函数y=和y=在第一象限内,点P在y=的图象上,PC垂直于X轴于点C,交y=的图象于点A,PD垂直于Y轴于D,交y=的图象于点B,当点P在y=的图象上运动时,下列结论错误的是( )
A.△ODB与△OCA的面积相等
B.当点A是PC的中点时,点B一定是PD的中点
C.只有当四边形OCPB为正方形时,四边形PAOB的面积最大
D.=
12.若,则反比例函数与一次函数在同一坐标系中的大致图象可能是( )
A. B. C. D.
二、填空题
13.如图所示,点B是反比例函数图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是
14.如图1是某电路图,滑动变阻器的电阻为R,电功率为P,P关于R的反比例函数图象如图2所示.小明通过调节电阻,发现当从增加到时,电功率减少了,则当时, W.
15.如图,点在双曲线上,过点作轴于点是轴负半轴上的一个动点,则的面积为 .
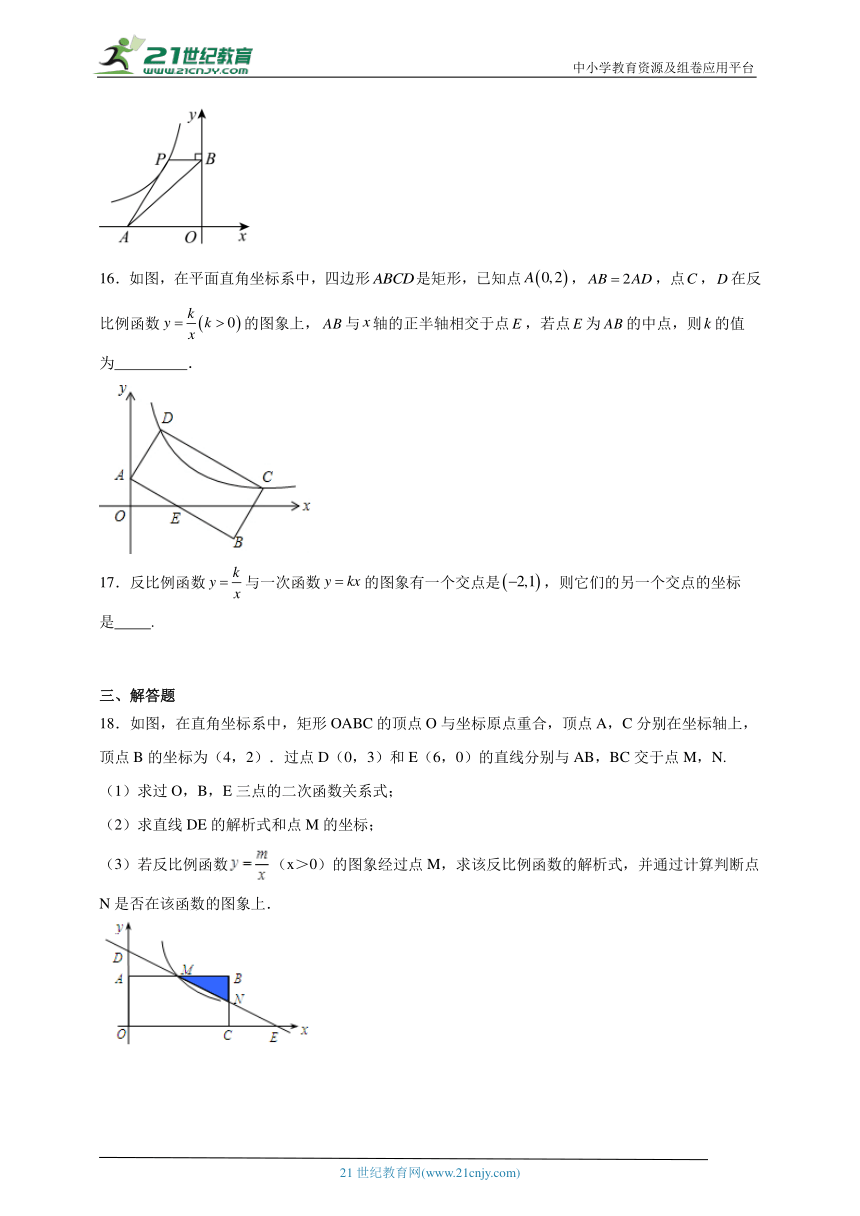
16.如图,在平面直角坐标系中,四边形是矩形,已知点,,点,在反比例函数的图象上,与轴的正半轴相交于点,若点为的中点,则的值为 .
17.反比例函数与一次函数的图象有一个交点是,则它们的另一个交点的坐标是 .
三、解答题
18.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
19.按要求在下列直角坐标系中画出一次函数和反比例函数的图象,并回答后面的问题.
x … 1 2 4 …
y … 4 2 1 …
(1)画图要求:
①用两点法直接描出一次函数与两坐标轴的交点,根据一次函数图象特征画出图象;
②用描点法画出反比例函数的图象:完成如下表格后直接描点连线.
(2)直接写出不等式的解集.
20.石阡是“中国苔茶之乡”,是茶树的原产地之一,有千年的茶叶栽种历史.某次茶艺比赛中指定使用的饮水机4分钟就可以将的饮用水加热到.此后停止加热,水温开始下降.如图所示,已知整个下降过程中水温与通电时间成反比例关系.
(1)在水温下降过程中,求y与x的函数解析式;
(2)比赛组织方要求,参赛选手必须把组织方提供的的饮用水用该款饮水机加热到,然后降温到方可使用.求从饮水机加热开始,到可以使用需要等待多长时间?
21.实验数据显示,一般成人喝50毫升白酒后,血液中酒精含量(毫克/百毫升)与时间(小时)变化的图如图(图由线段与部分双曲线组成)所示,国家规定,车辆驾驶人员血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”不能驾车上路.
(1)求线段和双曲线的函数表达式:
(2)假设某驾驶员晚上22时在家喝完50毫升白酒,第二天早上6点半能否驾车去上班?请说明理由.
22.如图,一次函数的图象与反比例函数(k为常数且)的图象交于,B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴的正半轴上,且,求点P的坐标.
23.如图,点A是反比例函数y=(m<0)位于第二象限的图象上的一个动点,过点A作AC⊥x轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图象及y轴分别交于B、D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为4,当四边形ABCD是正方形时,求直线AB的函数表达式.
24.如图,在平面直角坐标系中,已知一次函数y=kx+b(k>0,b>0)的图象与x轴交于A,与y轴交于C.双曲线y=(x>0)的图象交一次函数的图像于第一象限内的点B,BD⊥x轴于D. E是AB中点,直线DE交y轴于F,连接AF.
(1)若k=1, 点B(2,6)时.
①求一次函数和反比例函数的解析式;
②求AFD的面积.
(2)当 k=2, a=12时, 求AFD的面积.
(3)求证:当k,b,a为任意常数时,AFD的面积恒等于
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B A D B B B A
题号 11 12
答案 C A
1.C
【详解】y=-,反比例函数图像位于第二、四象限,在每个象限内,y随着x的增大而增大,
∵x1<x2<0,∴0<y1<y2,
∵x3>0,∴y3<0,
∴y3<y1<y2.
故选C.
点睛:掌握反比例函数的图像和性质是解本题的关键.
2.A
【分析】反比例函数中的时位于第二、四象限,在每个象限内,y随x的增大而增大;在不同象限内,y随x的增大而增大,根据这个性质选择则可.
【详解】解:A、因为,所以函数图象位于二、四象限,在每一象限内y随x的增大而增大,所以当时,y随x增大而增大,故本选项正确;
B、因为,故本选项错误;
C、因为,所以函数图象位于二、四象限,故本选项错误;
D、因为当时,,当时,,所以当时,或,故本选项错误;
故选:A.
【点睛】本题考查了反比例函数图象的性质:①当时,图象分别位于第一、三象限;当时,图象分别位于第二、四象限.②当时,在同一个象限内,y随x的增大而减小;当时,在同一个象限,y随x的增大而增大.注意反比例函数的图象应分在同一象限和不在同一象限两种情况分析.
3.D
【详解】试题分析:由反比例函数的性质列出不等式,解出k的范围,即可判断.
解:根据题意,k 1>0,
解得k>1;
∴k=3满足题意.
故选D.
4.B
【分析】由题意根据角平分线的性质可知,进而可得,勾股定理求得,进而求得,进而求得点的坐标,即可求得
【详解】如图,过分别作的垂线,垂足分别为,,
平分,平分,
,
,
,
四边形是正方形
,,
故选B
【点睛】本题考查了反比例函数的定义,正方形的判定,角平分线的性质,HL判定三角形全等以及全等的性质,勾股定理,理解角平分线的性质是解题的关键.
5.A
【分析】根据函数与图象的一个交点的横、纵坐标分别为a、b,可得,再根据分式的加减运算计算,即可求解.
【详解】解:∵函数与图象的一个交点的横、纵坐标分别为a、b,
∴,,
∴,
∴,
故选A.
【点睛】本题考查了反比例函数和一次函数的交点问题,分式的加减运算,理解交点坐标适合解析式是解题的关键.
6.D
【详解】试题解析:∵正比例函数和反比例函数均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(-3,-2),
∴另一个交点的坐标是(3,2),
故选D.
考点:反比例函数与一次函数的交点问题.
7.B
【分析】利用待定系数法解答,即可求解.
【详解】解:设该反比例函数的表达式是,
把点代入得:
,
解得:,
∴该反比例函数的表达式是.
故选:B.
【点睛】本题主要考查了求反比例函数解析式,熟练掌握待定系数法求函数解析式是解题的关键.
8.B
【分析】根据反比例函数的性质得k>0,然后根据一次函数的进行判断直线y=kx-k不经过的象限.
【详解】∵反比例函数y=的图象在一、三象限,
∴k>0,
∴直线y=kx﹣k经过第一、三、四象限,即不经过第二象限.
故选B.
【点睛】考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=(k为常数,k≠0);把已知条件(自变量与函数的对应值)代入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.也考查了反比例函数与一次函数的性质.
9.B
【分析】根据反比例函数的性质可得:函数的图象在第一三象限,由一次函数与系数的关系可得函数y=x+1的图象在第一三四象限,进而选出答案.
【详解】解:∵一次函数的图象经过第一、二、三象限,反比例函数的图象位于第一、三象限.
∴B图象正确.
故选B.
【点睛】此题考查了反比例函数的图象,以及一次函数的图象,熟练掌握各函数的图象与性质是解本题的关键.
10.A
【分析】根据反比例函数的性质,可以得到关于m的不等式,从而求得m的取值范围.
【详解】∵点均为反比例函数图象上的两点,当时,,
∴m-1<0,
∴m<1,
故选:A.
【点睛】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的增减性解答.
11.C
【分析】根据反比例函数的图象和性质,特别是根据反比例函数k的几何意义,对四个选项逐一进行分析,即可得出正确答案.
【详解】A、由于点A和点D均在同一个反比例函数y=的图象上,所以S△ODB=,S△OCA=;故△ODB与△OCA的面积相等,故A正确;
B、连接OP,点A是PC的中点,
则△OAP和△OAC的面积相等,
∵△ODP的面积=△OCP的面积=,△ODB与△OCA的面积相等,
∴△OBP与△OAP的面积相等,
∴△OBD和△OBP面积相等,
∴点B一定是PD的中点,故B正确;
C、由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不会发生变化,故C错误;
D、设P(m,),则A(m,),B(,),则CA=,PA=﹣,DB=,PB=m﹣,
故,,
∴,故D正确.
故选C.
【点睛】本题考查了反比例函数的综合题,关键是设P点坐标,利用点与点的坐标关系,反比例函数的性质表示相关线段的长,对每一个结论进行判断.
12.A
【分析】根据可知图象在第一、三象限,根据a,b同号判断出的图象经过的象限,即可求解.
【详解】解:,
的图象在第一、三象限,排除B,D;
,
a,b同号,
当,时,的图象经过第一、二、三象限,
当,时,的图象经过第二、三、四象限,
综上可知,只有A选项符合条件,
故选A.
【点睛】本题考查一次函数与反比例函数图象的综合判断,解题的关键是掌握一次函数和反比例函数的图象与系数的关系.
13.
【分析】本题考查了反比例函数系数k的几何意义,根据反比例函数的几何意义可知,矩形的面积为即为比例系数k的绝对值,根据图象所在象限即可判断出k的值.
【详解】解:由题意可知,
反比例函数图象的一个分支在第四象限,
,函数关系式为,
故答案为:.
14.16
【分析】本题考查了反比例函数的应用,正确求出与的函数关系式是解答本题的关键.根据反比例函数的图象的性质结合题意可得方程,据此可得的值,进而得出的值,再把代入函数关系式解答即可.
【详解】解:根据题意得:,
解得,
,
,
当时,,
即当时,的值为.
故答案为:16.
15.4
【分析】本题考查了反比例函数系数k的几何意义,由题意可得中为底,为高,利用三角形的面积公式求出即可.
【详解】解:把代入,得,
∴点的坐标为,
∵轴,
∴轴,
∴点的坐标为,
∴,
,
故答案为:4.
16.
【分析】证得△AOE≌△BHE≌△DFA≌△BGC,得出BH=BG=DF=OA=2,EH=CG=OE=AF= 2,即可求得D和C的坐标,然后由反比例函数图象上点的横纵坐标的乘积等于k列出方程组,通过解方程组可以求得k的值.
【详解】解:如图,作DF⊥y轴于F,过B点作x轴的平行线与过C点垂直与x轴的直线交于G,CG交x轴于K,作BH⊥x轴于H,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠DAF+∠OAE=90°,
∵∠AEO+∠OAE=90°,
∴∠DAF=∠AEO,
∵AB=2AD,E为AB的中点,
∴AD=AE,
在△ADF和△EAO中,
∴△ADF≌△EAO(AAS),
∴DF=OA=2,AF=OE,
∴D(2,),
∴AF= 2,
同理;△AOE≌△BHE,△ADF≌△CBG,
∴BH=BG=DF=OA=2,EH=CG=OE=AF= 2,
∴OK=2( 2)+2=k 2,CK=
∴C(k 2,),
∴(k 2)()=2 ,
解得k1=,k2=,
∵ 2>0,即,
∴k=,
故答案是:.
【点睛】本题考查了矩形的性质和反比例函数图象上点的坐标特征.图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
17.
【分析】将点( 2,1)代入反比例函数和一次函数中,分别求出反比例函数和一次函数的解析式,然后将两个解析式联立起来即可求得另一个交点坐标.
【详解】解:将点( 2,1)代入反比例函数中可得:k=-2,所以反比例函数解析式为,
将点( 2,1)代入一次函数中可得:k=,所以一次函数解析式为,
联立两个解析式可得:,解得:或,
则它们的另一个交点的坐标是:.
【点睛】本题考查待定系数法求反比例函数、一次函数的解析式以及它们的交点问题,比较简单,要熟练掌握.
18.(1)y=﹣x2+x;(2)直线DE的解析式为:y=﹣x+3;M(2,2);(3)点N在函数y=的图象上.
【分析】(1)首先把O(0,0),B(4,2),E(6,0)代入y=ax2+bx+c,可得 ,解此方程即可求得答案;
(2)首先设直线DE的解析式为:y=kx+b,然后将点D,E的坐标代入即可求得直线DE的解析式,又由点M在AB边上,B(4,2),而四边形OABC是矩形,可得点M的纵坐标为2,继而求得点M的坐标;
(3)由反比例函数y=(x>0)的图象经过点M,即可求得该反比例函数的解析式,又由点N在BC边上,B(4,2),可得点N的横坐标为4.然后由点N在直线y=-x+3上,求得点N的坐标,即可判断点N是否在该函数的图象上.
【详解】(1)设过O,B,E三点的二次函数关系式为:y=ax2+bx+c;
把O(0,0),B(4,2),E(6,0)代入y=ax2+bx+c,得
,
解得: ,
∴过O,B,E三点的二次函数关系式为:;
(2)设直线DE的解析式为:y=kx+b,
∵点D,E的坐标为(0,3)、(6,0),
∴,解得: ,
∴直线DE的解析式为:y=-x+3;
∵点M在AB边上,B(4,2),而四边形OABC是矩形,
∴点M的纵坐标为2.
又∵点M在直线y=-x+3上,
∴2=-x+3.
∴x=2.
∴M(2,2);
(3)∵y=(x>0)经过点M(2,2),
∴m=4.
∴该反比例函数的解析式为:y=,
又∵点N在BC边上,B(4,2),
∴点N的横坐标为4.
∵点N在直线y=-x+3上,
∴y=1.
∴N(4,1).
∵当x=4时,y==1,
∴点N在函数y=的图象上.
【点睛】考查了反比例函数的性质、待定系数法求函数的解析式以及矩形的性质等知识.此题综合性较强,难度适中,注意掌握数形结合思想与方程思想的应用.
19.(1)①见解析;②见解析
(2)或
【分析】(1)①利用一次函数解析式得出两个交点,然后连线即可;②根据反比例函数的解析式列表、描点、连线即可;
(2)根据题意直接利用(1)中函数图象即可得出不等式的解集.
【详解】(1)解:①一次函数y=x+1,
当x=0时,y=1,
当y=1时,x=-1,
∴一次函数经过点A(0,1),B(-1,0),在坐标系中描出点连接即可;
②列表如下:结合题干中已知的表格,描点,连线,如图所示即为所求;
x … -4 -2 -1
y … -1 -2 -4
(2),即反比例函数值大于一次函数值,
根据(1)中函数图象可得:或.
【点睛】题目主要考查作一次函数与反比例函数的图象,根据图象求不等式的解集,理解题意,熟练掌握作函数图象的基本方法是解题关键.
20.(1)
(2)
【分析】本题考查反比例函数的应用,正确掌握相关性质内容是解题的关键:
(1)利用待定系数法即可求出y与x的函数解析式;
(2)令(1)中求得的函数解析式,求出x的值即为需要等待的时间.
【详解】(1)解:∵整个下降过程中水温与通电时间成反比例关系,
∴可设整个下降过程中水温y,
∵其图象过点,
∴,
解得,
∴在水温下降过程中,;
(2)解:依题意,令,得,
解得,
答:从饮水机加热开始,到可以使用需要等待.
21.(1),
(2)不能,理由见详解
【分析】本题为一次函数和反比例函数的应用,涉及待定系数法等知识点.掌握自变量、函数值等知识是解题的关键.本题难度不大,较易得分.
(1)首先求得线段所在直线的解析式,然后求得点的坐标,代入反比例函数的解析式即可求解;
(2)把代入反比例函数解析式可求得时间,结合规定可进行判断.
【详解】(1)解:依题意,
直线过,则设直线的解析式
把代入
解得
∴,
当时,,即,
设双曲线的解析式为,
将点代入得:,
;
(2)解:由得当时,,
从22时到第二天早上6点时间间距为8.5小时,
,
第二天早上不能驾车去上班.
22.(1)
(2)
【分析】本题是一次函数和反比例函数综合题:
(1)利用点A在上求a,进而代入反比例函数求k.
(2)联立方程求出交点,设出点P坐标表示三角形面积,求出P点坐标.
【详解】(1)解:把点代入,得,
∴
把代入反比例函数(k为常数且)
∴,
∴反比例函数的表达式为;
(2)解:联立两个函数的表达式得,
解得或,
∴点B的坐标为
当时,得
∴点
设点P的坐标为
∵
∴
解得,(舍去),
∴点.
23.(1)B(2n,);(2)见解析;(3)y=x+
【分析】(1)由点A在双曲线上,确定出A坐标,进而得出 B的坐标,即可得出结论;
(2)由(1)得到的点B,D,M的坐标判断出,得出四边形ABCD是平行四边形,再用即可;
(3)由(2)结合建立方程求出n,m,从而得到点B,A的坐标即可.
【详解】(1)当时,,
,
由题意知,BD是AC的中垂线,
点B的纵坐标是,
把代入得,
B(2n,);
(2)证明:∵BD⊥AC,AC⊥x轴,
∴BD⊥y轴,由(1)知,B(2n,),A(n,),
∴D(0,),M(n,),
∴BM=MD=﹣n,
∵AC⊥x轴,
∴C(n,0),
∴AM=CM,
∴四边形ABCD是平行四边形.
又∵BD⊥AC,
∴平行四边形ABCD是菱形;
(3)当四边形ABCD是正方形时,
为等腰直角三角形,
,
的面积是4,
,
,
为线段AC的中点,
,
,
,
设直线AB的解析式为,
,
解得
直线AB的函数表达式为y=x+.
【点睛】此题是反比例函数综合题,主要考查了待定系数法,菱形的性质,正方形的性质,等腰三角形的性质,三角形的面积公式,解本题的关键是用m,n表示出点A,B,D,M的坐标.
24.(1)①y=x+4,; ②6;(2)6;(3)见解析
【分析】(1)①把点B(2,6)分别代入y=x+b和y=kx(x>0),根据待定系数法即可求得;
②求出D,E的坐标,求出直线DE的解析式,得到F点坐标,故可求出△ADF的面积;
(2)联立两函数求出B点坐标,再得到E点坐标,求出直线DE的解析式,从而得到F点坐标,根据三角形的面积公式即可求出AFD的面积
(3)与(2)同理即可求解.
【详解】解:(1)①∵一次函数y=x+b的图象与反比例函数y=(x>0)的图象交于B,B(2,6),
∴6=2+b,6=,
∴b=4,a=12,
∴一次函数解析式为y=x+4,反比例函数解析式为;
②令一次函数y=x+4=0
解得x=-4
∴A(-4,0)
∵E是AB中点,B(2,6)
∴E(-1,3)
∵BD⊥x轴于D
∴D(2,0)
设直线DE的解析式为y=mx+n,代入E(-1,3)、D(2,0)得
解得
∴直线DE的解析式为y=-x+2,
令x=0,得y=2
∴F(0,2)
∴OF=2
∴AFD的面积为;
(2)∵一次函数y=2x+b,反比例函数
联立得2x+b=
∴2x2+bx-12=0
解得x=,(x=舍去)
∴B(,)
由A(,0)得到E(,)
∵D(,0)
设直线DE的解析式为y=mx+n,代入E(,)、D(,0)得
解得
∴直线DE的解析式为y=-2x+,
令x=0,y=
∴F(0,)
∴OF=
∵A(,0),D(,0)
∴AD=+=
∴AFD的面积为;
(3)∵一次函数y=kx+b,反比例函数
联立得kx2+bx-a=0
解得x=,(x=舍去)
∴B(,)
由A(,0)得到E(,)
∵D(,0)
设直线DE的解析式为y=mx+n,代入E(,)、D(,0)得
解得
∴直线DE的解析式为y=-kx+,
令x=0,y=
∴F(0,)
∴OF=
∵A(,0),D(,0)
∴AD=+=
∴AFD的面积为.
【点睛】本题是反比例函数与一次函数的交点问题,解题的关键是熟知待定系数法求函数的解析式,三角形的面积及一元二次方程的解法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十六章反比例函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.反比例函数图象上有三个点,其中,则的大小关系是 ( )
A. B.
C. D.
2.对于反比例函数,下列说法正确的是( )
A.当时,y随x增大而增大 B.图象经过点
C.图象位于第一、三象限 D.当时,
3.若反比例函数的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )
A.-3 B.-1 C.0 D.3
4.如图,已知点,,C是y轴上位于点B上方的一点,AD平分,BE平分,直线BE交AD于点D.若反比例函数的图像经过点D,则k的值是( )
A. B. C. D.
5.函数与图象的一个交点的横、纵坐标分别为a、b,则的值为( )
A. B. C.3 D.
6.若正比例函数y=kx(k≠0)与反比例函数y=(a≠0)的图象有两个交点,其中一个交点的坐标为(-3,-2),则另一个交点的坐标为( )
A.(2,3) B.(3,-2) C.(-2,3) D.(3,2)
7.反比例函数的图象经过点,则该反比例函数的表达式是( )
A. B. C. D.
8.已知反比例函数y=的图象在一、三象限,那么直线y=kx﹣k不经过第( )象限.
A.一 B.二 C.三 D.四
9.在同一平面直角坐标系中,函数与函数的图象可能是( )
A. B. C. D.
10.若点均为反比例函数(m为常数)图象上的两点,当时,,则m的取值范围是( )
A. B. C. D.任意实数
11.两个反比例函数y=和y=在第一象限内,点P在y=的图象上,PC垂直于X轴于点C,交y=的图象于点A,PD垂直于Y轴于D,交y=的图象于点B,当点P在y=的图象上运动时,下列结论错误的是( )
A.△ODB与△OCA的面积相等
B.当点A是PC的中点时,点B一定是PD的中点
C.只有当四边形OCPB为正方形时,四边形PAOB的面积最大
D.=
12.若,则反比例函数与一次函数在同一坐标系中的大致图象可能是( )
A. B. C. D.
二、填空题
13.如图所示,点B是反比例函数图象上一点,过点B分别作x轴、y轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是
14.如图1是某电路图,滑动变阻器的电阻为R,电功率为P,P关于R的反比例函数图象如图2所示.小明通过调节电阻,发现当从增加到时,电功率减少了,则当时, W.
15.如图,点在双曲线上,过点作轴于点是轴负半轴上的一个动点,则的面积为 .
16.如图,在平面直角坐标系中,四边形是矩形,已知点,,点,在反比例函数的图象上,与轴的正半轴相交于点,若点为的中点,则的值为 .
17.反比例函数与一次函数的图象有一个交点是,则它们的另一个交点的坐标是 .
三、解答题
18.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求过O,B,E三点的二次函数关系式;
(2)求直线DE的解析式和点M的坐标;
(3)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上.
19.按要求在下列直角坐标系中画出一次函数和反比例函数的图象,并回答后面的问题.
x … 1 2 4 …
y … 4 2 1 …
(1)画图要求:
①用两点法直接描出一次函数与两坐标轴的交点,根据一次函数图象特征画出图象;
②用描点法画出反比例函数的图象:完成如下表格后直接描点连线.
(2)直接写出不等式的解集.
20.石阡是“中国苔茶之乡”,是茶树的原产地之一,有千年的茶叶栽种历史.某次茶艺比赛中指定使用的饮水机4分钟就可以将的饮用水加热到.此后停止加热,水温开始下降.如图所示,已知整个下降过程中水温与通电时间成反比例关系.
(1)在水温下降过程中,求y与x的函数解析式;
(2)比赛组织方要求,参赛选手必须把组织方提供的的饮用水用该款饮水机加热到,然后降温到方可使用.求从饮水机加热开始,到可以使用需要等待多长时间?
21.实验数据显示,一般成人喝50毫升白酒后,血液中酒精含量(毫克/百毫升)与时间(小时)变化的图如图(图由线段与部分双曲线组成)所示,国家规定,车辆驾驶人员血液中的酒精含量大于或等于20(毫克/百毫升)时属于“酒后驾驶”不能驾车上路.
(1)求线段和双曲线的函数表达式:
(2)假设某驾驶员晚上22时在家喝完50毫升白酒,第二天早上6点半能否驾车去上班?请说明理由.
22.如图,一次函数的图象与反比例函数(k为常数且)的图象交于,B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴的正半轴上,且,求点P的坐标.
23.如图,点A是反比例函数y=(m<0)位于第二象限的图象上的一个动点,过点A作AC⊥x轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图象及y轴分别交于B、D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为4,当四边形ABCD是正方形时,求直线AB的函数表达式.
24.如图,在平面直角坐标系中,已知一次函数y=kx+b(k>0,b>0)的图象与x轴交于A,与y轴交于C.双曲线y=(x>0)的图象交一次函数的图像于第一象限内的点B,BD⊥x轴于D. E是AB中点,直线DE交y轴于F,连接AF.
(1)若k=1, 点B(2,6)时.
①求一次函数和反比例函数的解析式;
②求AFD的面积.
(2)当 k=2, a=12时, 求AFD的面积.
(3)求证:当k,b,a为任意常数时,AFD的面积恒等于
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B A D B B B A
题号 11 12
答案 C A
1.C
【详解】y=-,反比例函数图像位于第二、四象限,在每个象限内,y随着x的增大而增大,
∵x1<x2<0,∴0<y1<y2,
∵x3>0,∴y3<0,
∴y3<y1<y2.
故选C.
点睛:掌握反比例函数的图像和性质是解本题的关键.
2.A
【分析】反比例函数中的时位于第二、四象限,在每个象限内,y随x的增大而增大;在不同象限内,y随x的增大而增大,根据这个性质选择则可.
【详解】解:A、因为,所以函数图象位于二、四象限,在每一象限内y随x的增大而增大,所以当时,y随x增大而增大,故本选项正确;
B、因为,故本选项错误;
C、因为,所以函数图象位于二、四象限,故本选项错误;
D、因为当时,,当时,,所以当时,或,故本选项错误;
故选:A.
【点睛】本题考查了反比例函数图象的性质:①当时,图象分别位于第一、三象限;当时,图象分别位于第二、四象限.②当时,在同一个象限内,y随x的增大而减小;当时,在同一个象限,y随x的增大而增大.注意反比例函数的图象应分在同一象限和不在同一象限两种情况分析.
3.D
【详解】试题分析:由反比例函数的性质列出不等式,解出k的范围,即可判断.
解:根据题意,k 1>0,
解得k>1;
∴k=3满足题意.
故选D.
4.B
【分析】由题意根据角平分线的性质可知,进而可得,勾股定理求得,进而求得,进而求得点的坐标,即可求得
【详解】如图,过分别作的垂线,垂足分别为,,
平分,平分,
,
,
,
四边形是正方形
,,
故选B
【点睛】本题考查了反比例函数的定义,正方形的判定,角平分线的性质,HL判定三角形全等以及全等的性质,勾股定理,理解角平分线的性质是解题的关键.
5.A
【分析】根据函数与图象的一个交点的横、纵坐标分别为a、b,可得,再根据分式的加减运算计算,即可求解.
【详解】解:∵函数与图象的一个交点的横、纵坐标分别为a、b,
∴,,
∴,
∴,
故选A.
【点睛】本题考查了反比例函数和一次函数的交点问题,分式的加减运算,理解交点坐标适合解析式是解题的关键.
6.D
【详解】试题解析:∵正比例函数和反比例函数均关于原点对称,
∴两函数的交点关于原点对称,
∵一个交点的坐标是(-3,-2),
∴另一个交点的坐标是(3,2),
故选D.
考点:反比例函数与一次函数的交点问题.
7.B
【分析】利用待定系数法解答,即可求解.
【详解】解:设该反比例函数的表达式是,
把点代入得:
,
解得:,
∴该反比例函数的表达式是.
故选:B.
【点睛】本题主要考查了求反比例函数解析式,熟练掌握待定系数法求函数解析式是解题的关键.
8.B
【分析】根据反比例函数的性质得k>0,然后根据一次函数的进行判断直线y=kx-k不经过的象限.
【详解】∵反比例函数y=的图象在一、三象限,
∴k>0,
∴直线y=kx﹣k经过第一、三、四象限,即不经过第二象限.
故选B.
【点睛】考查了待定系数法求反比例函数的解析式:设出含有待定系数的反比例函数解析式y=(k为常数,k≠0);把已知条件(自变量与函数的对应值)代入解析式,得到待定系数的方程;解方程,求出待定系数;写出解析式.也考查了反比例函数与一次函数的性质.
9.B
【分析】根据反比例函数的性质可得:函数的图象在第一三象限,由一次函数与系数的关系可得函数y=x+1的图象在第一三四象限,进而选出答案.
【详解】解:∵一次函数的图象经过第一、二、三象限,反比例函数的图象位于第一、三象限.
∴B图象正确.
故选B.
【点睛】此题考查了反比例函数的图象,以及一次函数的图象,熟练掌握各函数的图象与性质是解本题的关键.
10.A
【分析】根据反比例函数的性质,可以得到关于m的不等式,从而求得m的取值范围.
【详解】∵点均为反比例函数图象上的两点,当时,,
∴m-1<0,
∴m<1,
故选:A.
【点睛】本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的增减性解答.
11.C
【分析】根据反比例函数的图象和性质,特别是根据反比例函数k的几何意义,对四个选项逐一进行分析,即可得出正确答案.
【详解】A、由于点A和点D均在同一个反比例函数y=的图象上,所以S△ODB=,S△OCA=;故△ODB与△OCA的面积相等,故A正确;
B、连接OP,点A是PC的中点,
则△OAP和△OAC的面积相等,
∵△ODP的面积=△OCP的面积=,△ODB与△OCA的面积相等,
∴△OBP与△OAP的面积相等,
∴△OBD和△OBP面积相等,
∴点B一定是PD的中点,故B正确;
C、由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不会发生变化,故C错误;
D、设P(m,),则A(m,),B(,),则CA=,PA=﹣,DB=,PB=m﹣,
故,,
∴,故D正确.
故选C.
【点睛】本题考查了反比例函数的综合题,关键是设P点坐标,利用点与点的坐标关系,反比例函数的性质表示相关线段的长,对每一个结论进行判断.
12.A
【分析】根据可知图象在第一、三象限,根据a,b同号判断出的图象经过的象限,即可求解.
【详解】解:,
的图象在第一、三象限,排除B,D;
,
a,b同号,
当,时,的图象经过第一、二、三象限,
当,时,的图象经过第二、三、四象限,
综上可知,只有A选项符合条件,
故选A.
【点睛】本题考查一次函数与反比例函数图象的综合判断,解题的关键是掌握一次函数和反比例函数的图象与系数的关系.
13.
【分析】本题考查了反比例函数系数k的几何意义,根据反比例函数的几何意义可知,矩形的面积为即为比例系数k的绝对值,根据图象所在象限即可判断出k的值.
【详解】解:由题意可知,
反比例函数图象的一个分支在第四象限,
,函数关系式为,
故答案为:.
14.16
【分析】本题考查了反比例函数的应用,正确求出与的函数关系式是解答本题的关键.根据反比例函数的图象的性质结合题意可得方程,据此可得的值,进而得出的值,再把代入函数关系式解答即可.
【详解】解:根据题意得:,
解得,
,
,
当时,,
即当时,的值为.
故答案为:16.
15.4
【分析】本题考查了反比例函数系数k的几何意义,由题意可得中为底,为高,利用三角形的面积公式求出即可.
【详解】解:把代入,得,
∴点的坐标为,
∵轴,
∴轴,
∴点的坐标为,
∴,
,
故答案为:4.
16.
【分析】证得△AOE≌△BHE≌△DFA≌△BGC,得出BH=BG=DF=OA=2,EH=CG=OE=AF= 2,即可求得D和C的坐标,然后由反比例函数图象上点的横纵坐标的乘积等于k列出方程组,通过解方程组可以求得k的值.
【详解】解:如图,作DF⊥y轴于F,过B点作x轴的平行线与过C点垂直与x轴的直线交于G,CG交x轴于K,作BH⊥x轴于H,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠DAF+∠OAE=90°,
∵∠AEO+∠OAE=90°,
∴∠DAF=∠AEO,
∵AB=2AD,E为AB的中点,
∴AD=AE,
在△ADF和△EAO中,
∴△ADF≌△EAO(AAS),
∴DF=OA=2,AF=OE,
∴D(2,),
∴AF= 2,
同理;△AOE≌△BHE,△ADF≌△CBG,
∴BH=BG=DF=OA=2,EH=CG=OE=AF= 2,
∴OK=2( 2)+2=k 2,CK=
∴C(k 2,),
∴(k 2)()=2 ,
解得k1=,k2=,
∵ 2>0,即,
∴k=,
故答案是:.
【点睛】本题考查了矩形的性质和反比例函数图象上点的坐标特征.图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
17.
【分析】将点( 2,1)代入反比例函数和一次函数中,分别求出反比例函数和一次函数的解析式,然后将两个解析式联立起来即可求得另一个交点坐标.
【详解】解:将点( 2,1)代入反比例函数中可得:k=-2,所以反比例函数解析式为,
将点( 2,1)代入一次函数中可得:k=,所以一次函数解析式为,
联立两个解析式可得:,解得:或,
则它们的另一个交点的坐标是:.
【点睛】本题考查待定系数法求反比例函数、一次函数的解析式以及它们的交点问题,比较简单,要熟练掌握.
18.(1)y=﹣x2+x;(2)直线DE的解析式为:y=﹣x+3;M(2,2);(3)点N在函数y=的图象上.
【分析】(1)首先把O(0,0),B(4,2),E(6,0)代入y=ax2+bx+c,可得 ,解此方程即可求得答案;
(2)首先设直线DE的解析式为:y=kx+b,然后将点D,E的坐标代入即可求得直线DE的解析式,又由点M在AB边上,B(4,2),而四边形OABC是矩形,可得点M的纵坐标为2,继而求得点M的坐标;
(3)由反比例函数y=(x>0)的图象经过点M,即可求得该反比例函数的解析式,又由点N在BC边上,B(4,2),可得点N的横坐标为4.然后由点N在直线y=-x+3上,求得点N的坐标,即可判断点N是否在该函数的图象上.
【详解】(1)设过O,B,E三点的二次函数关系式为:y=ax2+bx+c;
把O(0,0),B(4,2),E(6,0)代入y=ax2+bx+c,得
,
解得: ,
∴过O,B,E三点的二次函数关系式为:;
(2)设直线DE的解析式为:y=kx+b,
∵点D,E的坐标为(0,3)、(6,0),
∴,解得: ,
∴直线DE的解析式为:y=-x+3;
∵点M在AB边上,B(4,2),而四边形OABC是矩形,
∴点M的纵坐标为2.
又∵点M在直线y=-x+3上,
∴2=-x+3.
∴x=2.
∴M(2,2);
(3)∵y=(x>0)经过点M(2,2),
∴m=4.
∴该反比例函数的解析式为:y=,
又∵点N在BC边上,B(4,2),
∴点N的横坐标为4.
∵点N在直线y=-x+3上,
∴y=1.
∴N(4,1).
∵当x=4时,y==1,
∴点N在函数y=的图象上.
【点睛】考查了反比例函数的性质、待定系数法求函数的解析式以及矩形的性质等知识.此题综合性较强,难度适中,注意掌握数形结合思想与方程思想的应用.
19.(1)①见解析;②见解析
(2)或
【分析】(1)①利用一次函数解析式得出两个交点,然后连线即可;②根据反比例函数的解析式列表、描点、连线即可;
(2)根据题意直接利用(1)中函数图象即可得出不等式的解集.
【详解】(1)解:①一次函数y=x+1,
当x=0时,y=1,
当y=1时,x=-1,
∴一次函数经过点A(0,1),B(-1,0),在坐标系中描出点连接即可;
②列表如下:结合题干中已知的表格,描点,连线,如图所示即为所求;
x … -4 -2 -1
y … -1 -2 -4
(2),即反比例函数值大于一次函数值,
根据(1)中函数图象可得:或.
【点睛】题目主要考查作一次函数与反比例函数的图象,根据图象求不等式的解集,理解题意,熟练掌握作函数图象的基本方法是解题关键.
20.(1)
(2)
【分析】本题考查反比例函数的应用,正确掌握相关性质内容是解题的关键:
(1)利用待定系数法即可求出y与x的函数解析式;
(2)令(1)中求得的函数解析式,求出x的值即为需要等待的时间.
【详解】(1)解:∵整个下降过程中水温与通电时间成反比例关系,
∴可设整个下降过程中水温y,
∵其图象过点,
∴,
解得,
∴在水温下降过程中,;
(2)解:依题意,令,得,
解得,
答:从饮水机加热开始,到可以使用需要等待.
21.(1),
(2)不能,理由见详解
【分析】本题为一次函数和反比例函数的应用,涉及待定系数法等知识点.掌握自变量、函数值等知识是解题的关键.本题难度不大,较易得分.
(1)首先求得线段所在直线的解析式,然后求得点的坐标,代入反比例函数的解析式即可求解;
(2)把代入反比例函数解析式可求得时间,结合规定可进行判断.
【详解】(1)解:依题意,
直线过,则设直线的解析式
把代入
解得
∴,
当时,,即,
设双曲线的解析式为,
将点代入得:,
;
(2)解:由得当时,,
从22时到第二天早上6点时间间距为8.5小时,
,
第二天早上不能驾车去上班.
22.(1)
(2)
【分析】本题是一次函数和反比例函数综合题:
(1)利用点A在上求a,进而代入反比例函数求k.
(2)联立方程求出交点,设出点P坐标表示三角形面积,求出P点坐标.
【详解】(1)解:把点代入,得,
∴
把代入反比例函数(k为常数且)
∴,
∴反比例函数的表达式为;
(2)解:联立两个函数的表达式得,
解得或,
∴点B的坐标为
当时,得
∴点
设点P的坐标为
∵
∴
解得,(舍去),
∴点.
23.(1)B(2n,);(2)见解析;(3)y=x+
【分析】(1)由点A在双曲线上,确定出A坐标,进而得出 B的坐标,即可得出结论;
(2)由(1)得到的点B,D,M的坐标判断出,得出四边形ABCD是平行四边形,再用即可;
(3)由(2)结合建立方程求出n,m,从而得到点B,A的坐标即可.
【详解】(1)当时,,
,
由题意知,BD是AC的中垂线,
点B的纵坐标是,
把代入得,
B(2n,);
(2)证明:∵BD⊥AC,AC⊥x轴,
∴BD⊥y轴,由(1)知,B(2n,),A(n,),
∴D(0,),M(n,),
∴BM=MD=﹣n,
∵AC⊥x轴,
∴C(n,0),
∴AM=CM,
∴四边形ABCD是平行四边形.
又∵BD⊥AC,
∴平行四边形ABCD是菱形;
(3)当四边形ABCD是正方形时,
为等腰直角三角形,
,
的面积是4,
,
,
为线段AC的中点,
,
,
,
设直线AB的解析式为,
,
解得
直线AB的函数表达式为y=x+.
【点睛】此题是反比例函数综合题,主要考查了待定系数法,菱形的性质,正方形的性质,等腰三角形的性质,三角形的面积公式,解本题的关键是用m,n表示出点A,B,D,M的坐标.
24.(1)①y=x+4,; ②6;(2)6;(3)见解析
【分析】(1)①把点B(2,6)分别代入y=x+b和y=kx(x>0),根据待定系数法即可求得;
②求出D,E的坐标,求出直线DE的解析式,得到F点坐标,故可求出△ADF的面积;
(2)联立两函数求出B点坐标,再得到E点坐标,求出直线DE的解析式,从而得到F点坐标,根据三角形的面积公式即可求出AFD的面积
(3)与(2)同理即可求解.
【详解】解:(1)①∵一次函数y=x+b的图象与反比例函数y=(x>0)的图象交于B,B(2,6),
∴6=2+b,6=,
∴b=4,a=12,
∴一次函数解析式为y=x+4,反比例函数解析式为;
②令一次函数y=x+4=0
解得x=-4
∴A(-4,0)
∵E是AB中点,B(2,6)
∴E(-1,3)
∵BD⊥x轴于D
∴D(2,0)
设直线DE的解析式为y=mx+n,代入E(-1,3)、D(2,0)得
解得
∴直线DE的解析式为y=-x+2,
令x=0,得y=2
∴F(0,2)
∴OF=2
∴AFD的面积为;
(2)∵一次函数y=2x+b,反比例函数
联立得2x+b=
∴2x2+bx-12=0
解得x=,(x=舍去)
∴B(,)
由A(,0)得到E(,)
∵D(,0)
设直线DE的解析式为y=mx+n,代入E(,)、D(,0)得
解得
∴直线DE的解析式为y=-2x+,
令x=0,y=
∴F(0,)
∴OF=
∵A(,0),D(,0)
∴AD=+=
∴AFD的面积为;
(3)∵一次函数y=kx+b,反比例函数
联立得kx2+bx-a=0
解得x=,(x=舍去)
∴B(,)
由A(,0)得到E(,)
∵D(,0)
设直线DE的解析式为y=mx+n,代入E(,)、D(,0)得
解得
∴直线DE的解析式为y=-kx+,
令x=0,y=
∴F(0,)
∴OF=
∵A(,0),D(,0)
∴AD=+=
∴AFD的面积为.
【点睛】本题是反比例函数与一次函数的交点问题,解题的关键是熟知待定系数法求函数的解析式,三角形的面积及一元二次方程的解法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
