27.2相似三角形同步练习(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
27.2相似三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
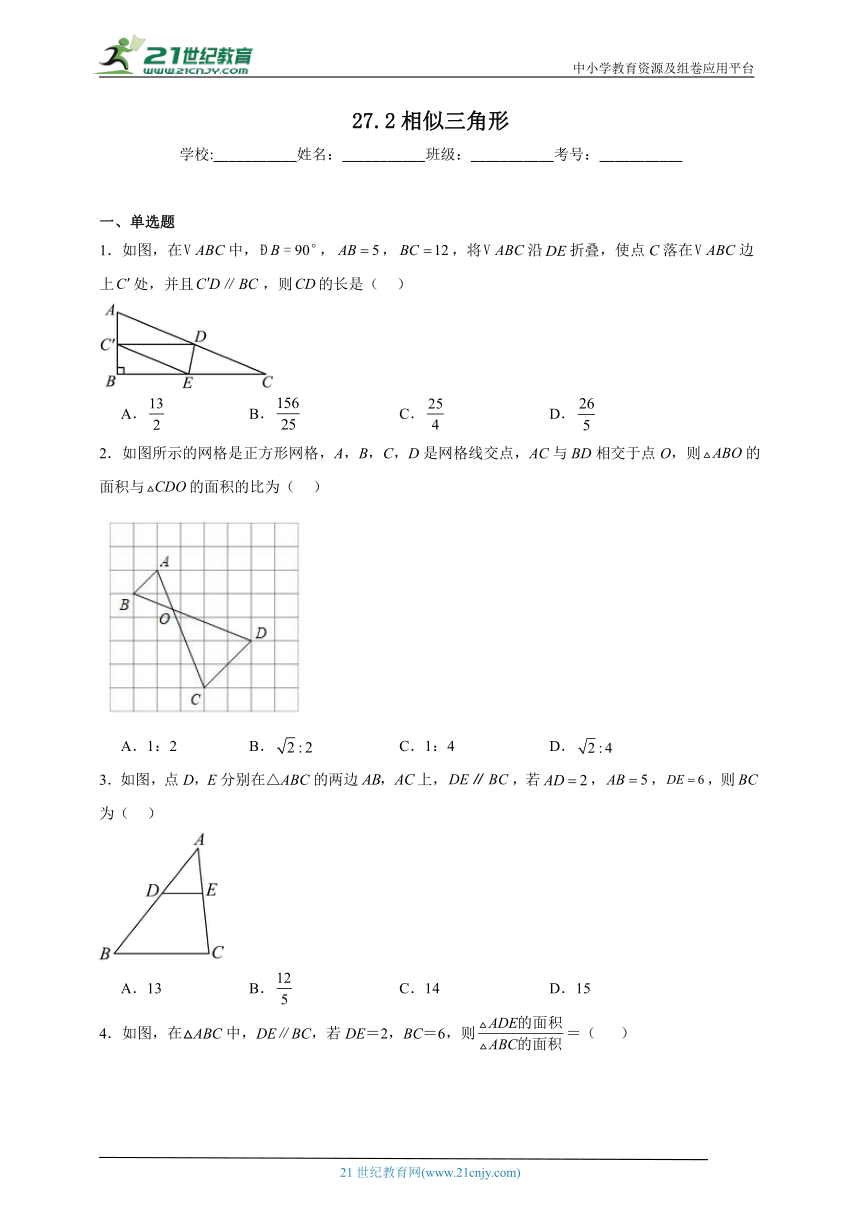
1.如图,在中,,,,将沿折叠,使点C落在边上处,并且,则的长是( )
A. B. C. D.
2.如图所示的网格是正方形网格,A,B,C,D是网格线交点,AC与BD相交于点O,则的面积与的面积的比为( )
A.1:2 B. C.1:4 D.
3.如图,点D,E分别在△ABC的两边上,,若,,,则为( )
A.13 B. C.14 D.15
4.如图,在△ABC中,DE∥BC,若DE=2,BC=6,则=( )
A. B. C. D.
5.如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是
A.b2=ac B.b2=ce C.be=ac D.bd=ae
6.如图,已知与都是等边三角形,点、、在同一直线上,连结交于点,连结分别与、交于点、,下列结论不一定成立的是( )
A. B. C. D.
7.如图,已知.若,则的度数为( )
A. B. C. D.
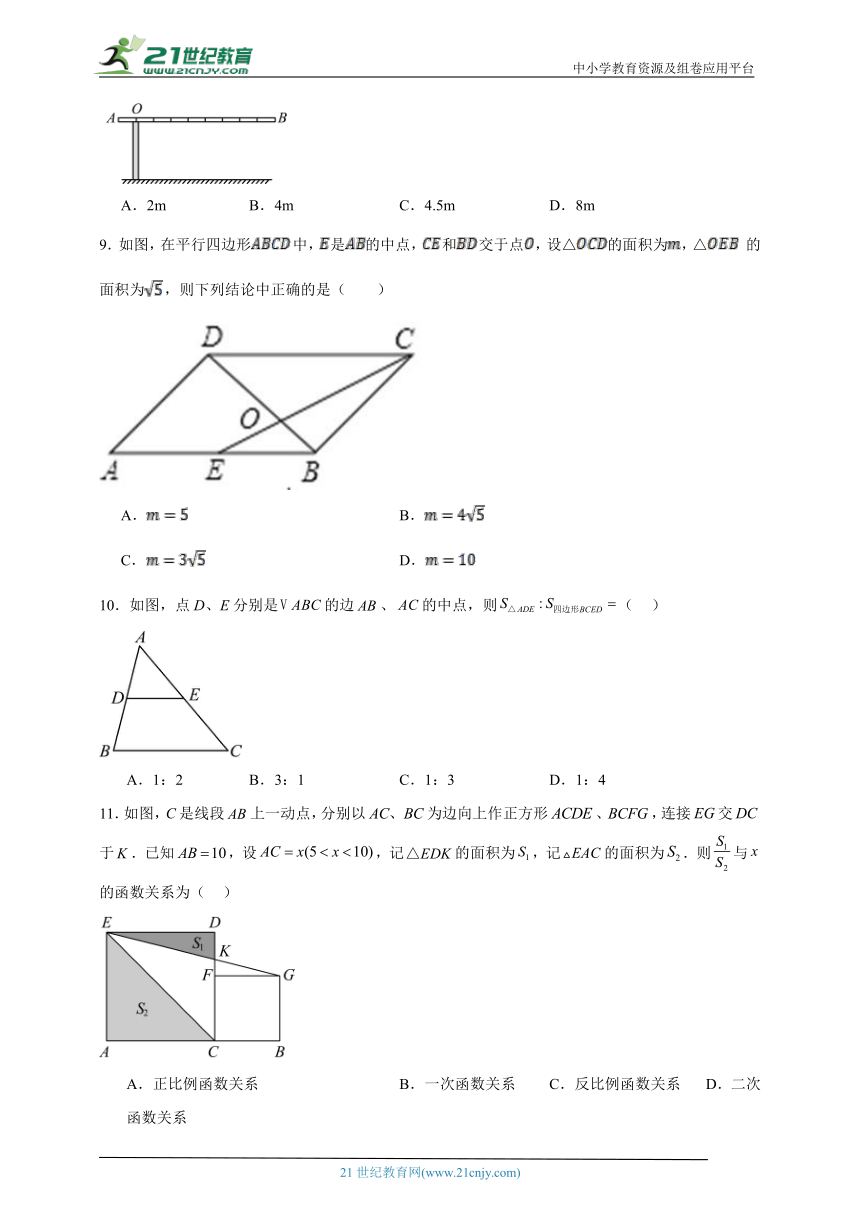
8.如图,铁道口的栏杆短臂OA长1m,长臂OB长8m.当短臂外端A下降0.5m时,长臂外端B升高( )
A.2m B.4m C.4.5m D.8m
9.如图,在平行四边形中,是的中点,和交于点,设△的面积为,△ 的面积为,则下列结论中正确的是( )
A. B.
C. D.
10.如图,点D、E分别是的边、的中点,则( )
A.1:2 B.3:1 C.1:3 D.1:4
11.如图,是线段上一动点,分别以为边向上作正方形、,连接交于.已知,设,记的面积为,记的面积为.则与的函数关系为( )
A.正比例函数关系 B.一次函数关系 C.反比例函数关系 D.二次函数关系
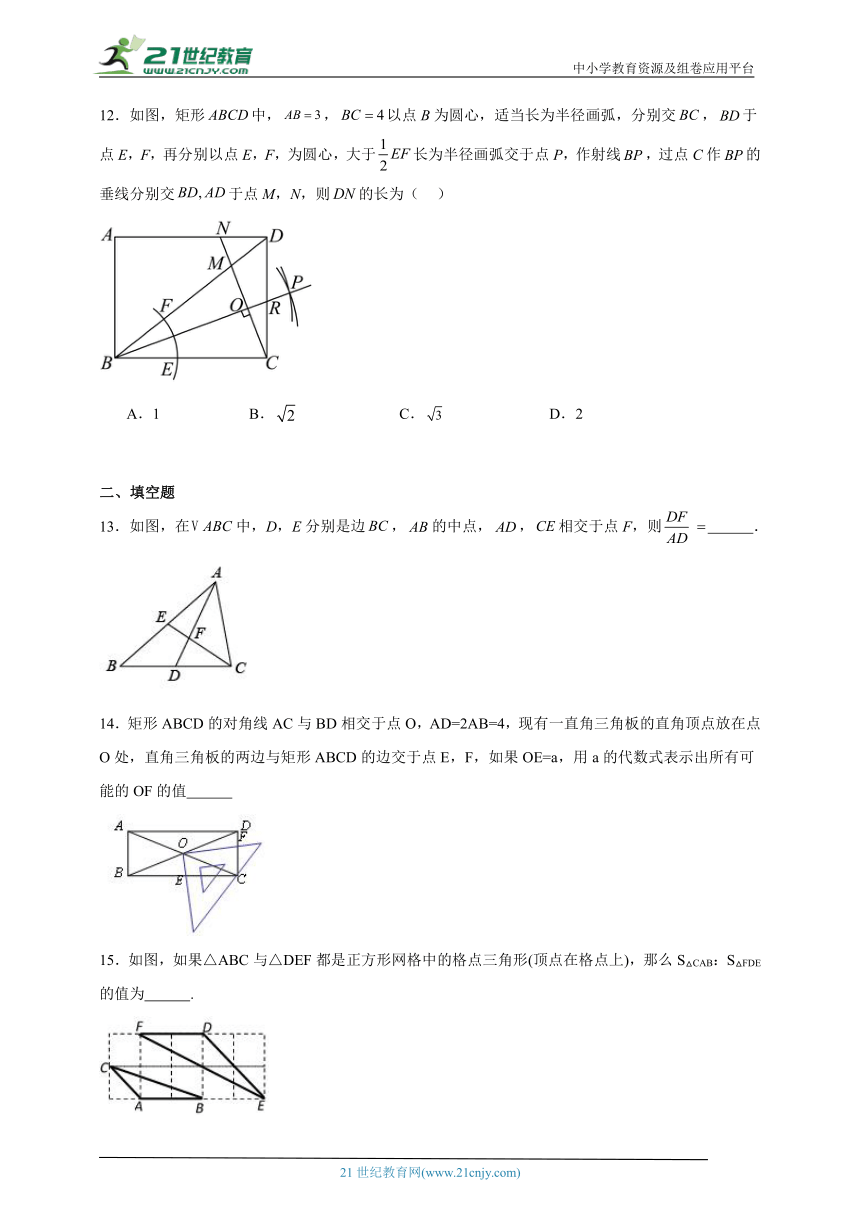
12.如图,矩形中,,以点B为圆心,适当长为半径画弧,分别交,于点E,F,再分别以点E,F,为圆心,大于长为半径画弧交于点P,作射线,过点C作的垂线分别交于点M,N,则的长为( )
A.1 B. C. D.2
二、填空题
13.如图,在中,D,E分别是边,的中点,,相交于点F,则 .
14.矩形ABCD的对角线AC与BD相交于点O,AD=2AB=4,现有一直角三角板的直角顶点放在点O处,直角三角板的两边与矩形ABCD的边交于点E,F,如果OE=a,用a的代数式表示出所有可能的OF的值
15.如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么S△CAB:S△FDE的值为 .
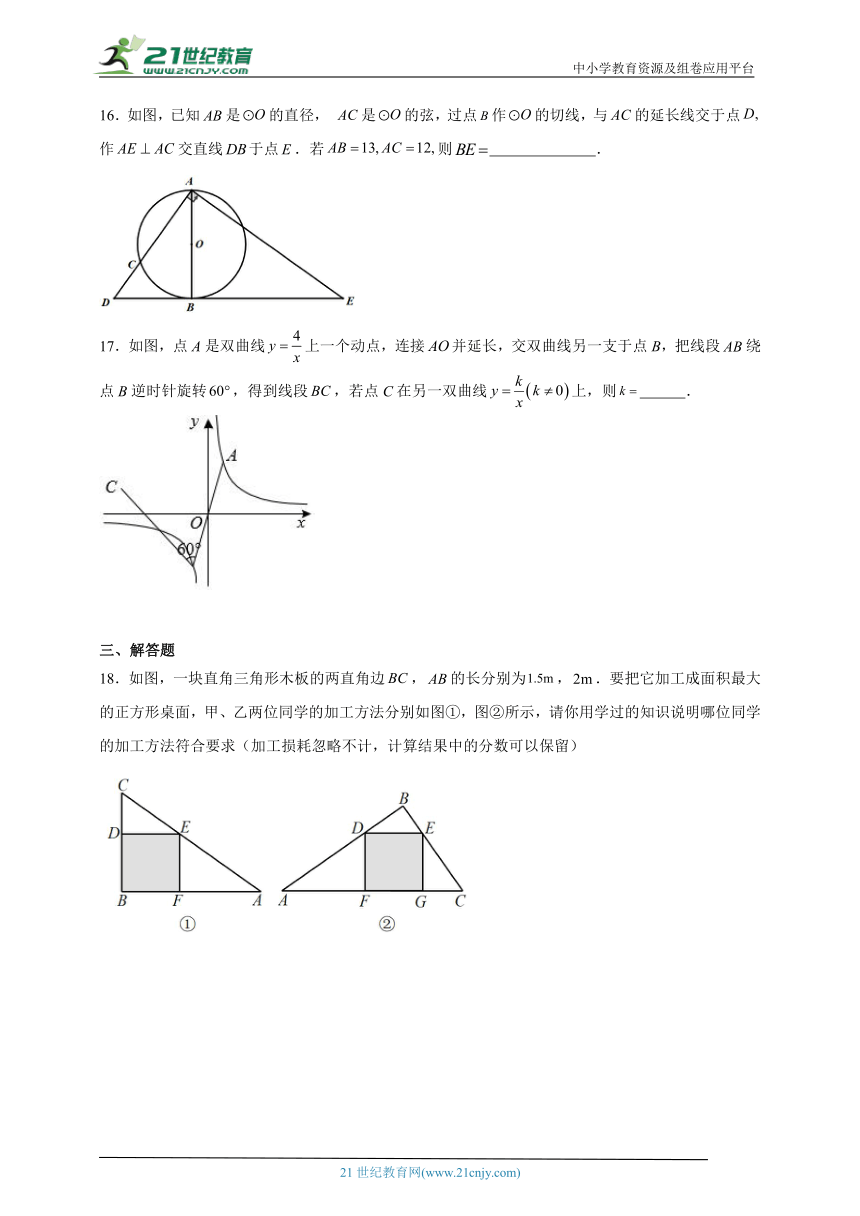
16.如图,已知是的直径, 是的弦,过点作的切线,与的延长线交于点作交直线于点.若则 .
17.如图,点A是双曲线上一个动点,连接并延长,交双曲线另一支于点B,把线段绕点B逆时针旋转,得到线段,若点C在另一双曲线上,则 .
三、解答题
18.如图,一块直角三角形木板的两直角边,的长分别为,.要把它加工成面积最大的正方形桌面,甲、乙两位同学的加工方法分别如图①,图②所示,请你用学过的知识说明哪位同学的加工方法符合要求(加工损耗忽略不计,计算结果中的分数可以保留)
19.已知中,,点为的中点.
(1)在线段上求作一点,使(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下求线段的长.
20.近期《黑神话:悟空》正式在全球上线,迅速吸引了全球游戏爱好者的目光,《黑神话:悟空》游戏中选取的27处山西极具代表性的古建筑,不仅展示了山西深厚的文化底蕴,也为当地文旅产业带来新的发展机遇,更为山西的文化元素提供了一个面向全球游戏玩家群体的数字化传播窗口.飞虹塔是山西省非常有名的一座塔楼,这座塔的位置位于山西省洪洞县广胜寺景区.某实践小组欲测量飞虹塔的高度,过程见下表.根据表格信息,求飞虹塔的大致高度.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
测量步骤 步骤1:把长为2米的标杆垂直立于地面点D处,塔尖点A和标杆顶端C确定的直线交水平于点Q,测得米; 步骤2:将标杆沿着的方向平移到点F处,塔尖点A和标杆顶端E确定的直线交直线于点P,测得米,米;(以上数据均为近似值)
21.课题:《杠杠原理与相似三角形》
杠杆原理:也称为“杠杆平衡条件”:杠杆原理是几何学在物理学的体现.
相关概念:
支点:杠杆绕着转动的固定点;
动力:使杠杆转动的力;
阻力:阻碍杠杆转动的力;
动力臂:从支点到动力作用线的距离;
阻力臂:从支点到阻力作用线的距离.
基本模型:当一个力通过一个支点施加在杠杆上时,通过作图,可以观察到两个相似的三角形
如图,因为,,
所以, 则有 ①
又因为(消耗的功一致),可得 ,所以
可得②______(为阻力的反作用力).
即,动力动力臂阻力阻力臂.
得出结论:要使杠杆平衡,作用在杠杆上的两个力矩(力与力臂的乘积)大小必须相等
(1)补全①、②所缺的内容,课题证明杠杆原理过程中运用到的几何知识是
(2)如图,小明用实心钢管制作了一个自带支点杠杆A-O-B,O为支点,,,,,方向上因撑起一物体产生450牛顿(国际单位制中,力的单位)的阻力,方向上施加一个力使杠杆平衡,.
请利用“动力臂”,“阻力臂”与“支点”概念构造相似三角形 ,并运用“杠杆原理”相关知识,求出的大小.
22.某数学小组为了测量云龙山上宝塔的高度,利用休息时间进行了实地测量:如图2,首先把长为2米的标杆垂直立于地面上的点处,当塔尖、标杆顶端与地面上的点在同一直线上时,米;再将标杆沿方向平移11米至点处(即米,米),当塔尖、标杆顶端与地面上的点在同一直线上时,米,已知,,,点、、、、在同一水平直线上,请你帮助这个数学小组求出云龙山上宝塔的高度.
23.如图,在中,
(1)求证:;
(2)试证明;(要求:证明过程注明理由)
24.已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D A C D B B C
题号 11 12
答案 B A
1.B
【分析】根据勾股定理就可以求出AC的值,再根据轴对称的性质就可以得出,由得出就可以得出就可以求出结论.
【详解】解:∵,由勾股定理,得.
∵与关于成轴对称,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
故选:B.
【点睛】本题考查了勾股定理的运用,轴对称的性质的运用,相似三角形的判定及性质的运用,解答时运用轴对称的性质求解是关键.
2.C
【分析】设小方格的边长为1,根据等腰直角三角形和勾股定理求出AB和CD的长,再根据
得到 ,然后利用相似三角形的性质来求解.
【详解】解:如下图,
设小方格的边长为1,
∵、分别是边长为1和2的等腰直角三角形,
∴,,.
∵,
∴,
∴.
又∵ ,
∴,
∴,
∴.
故选:C.
【点睛】本题考查相似三角形面积比与相似比的关系,关键是判断两三角形相似,确定其相似比.
3.D
【分析】本题考查了相似三角形的性质和判定,平行线的判定的应用,关键是推出.
首先证明出,然后得到,然后代数求解即可.
【详解】解:∵,
∴,
∴,即,
解得:,
故选D.
4.D
【分析】由DE∥BC知△ADE∽△ABC,然后根据相似比求解.
【详解】解:∵DE∥BC
∴△ADE∽△ABC.
又因为DE=2,BC=6,可得相似比为1:3.
即==.
故选D.
【点睛】本题主要是先证明两三角形相似,再根据已给的线段求相似比即可.
5.A
【详解】试题分析:∵CD∥AB,∴∠CDB=∠DBA.
又∵∠C=∠BDA=90°,∴△CDB∽△DBA.∴,即.
∴A、b2=ac,成立,故本选项正确;
B、b2=ac,不是b2=ce,故本选项错误;
C、be=ad,不是be=ac,故本选项错误;
D、bd=ac,不是bd=ae,故本选项错误.
故选A.
6.C
【分析】根据等边三角形的性质及相似三角形的判定可进行求解.
【详解】解:∵与都是等边三角形,
∴,
∴,
∴,即,且相似比为1,
∵,
∴,
∴,,
∴不一定成立;
故选C.
【点睛】本题主要考查相似三角形的性质与判定及等边三角形的性质,熟练掌握相似三角形的性质与判定及等边三角形的性质是解题的关键.
7.D
【分析】本题主要考查了相似三角形的性质,三角形的内角和定理,解答的关键是结合图形分析清楚各角的关系.
由相似可得,利用三角形的外角性质可求得,从而可求的度数.
【详解】解:∵,
,
故选:D.
8.B
【详解】设长臂外端B升高xm,根据三角形相似得,∴x=4,故选B.
9.B
【详解】∵ ∥,∴ △∽△.又∵ 是的中点,∴ ,
∴ :=,即.
10.C
【分析】本题考查了相似三角形的判定与性质,中位线的性质,现根据点D、E分别是的边、的中点,得是的中位线,即,且,即可作答.
【详解】解:∵点D、E分别是的边、的中点,
∴是的中位线,即,
∴,
则,
故,
那么,
故选:C.
11.B
【分析】四边形、是正方形,,设,可用含的式子表示,根据,可得,设,则,可求出,由此即可求解.
【详解】解:四边形、是正方形,,设,
∴,
∴,
∴,
设,则,
∵,
∴,
∴,即,解得,,
∴,
∴,
∴是关于的一次函数,
故选:.
【点睛】本题主要考查运用几何面积表示函数关系,掌握几何面积的计算方法是解题的关键.
12.A
【分析】先根据矩形的性质以及勾股定理得到,,,,再由作图过程知平分,进而证明,,则,再证明,即可求得的长.
【详解】矩形中,,,
,,,
,
由作图过程知平分,则,
,
,
,
,
,
,
,
,
,即,
,
故选:A.
【点睛】本题考查矩形的性质、勾股定理、角平分线的尺规作图、全等三角形的判定与性质、相似三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质以及判断出平分是解答的关键.
13.
【分析】连接,利用三角形的中位线定理,得到,得到,得到,进一步求解即可.
【详解】解:连接,
∵D,E分别是边,的中点,
则:,
∴,
∴,
∴;
故答案为:.
【点睛】本题考查相似三角形的判定和性质.解题的关键是添加辅助线,利用三角形的中位线定理,证明三角形相似.
14.
【详解】解:①当F为CD的中点时,OE=FC=FD=a=1,
∵O为BD的中点,∴OF∥BC,
∴△DFO∽△DCB,则=,OF=2,
②当F不是CD的中点时,作OM⊥BC,ON⊥CD,垂足分别为M、N,
∵∠MON=∠EOF=90°,
∴∠MOE=∠NOF,
∴△OME∽△ONF,==2,OF=2a,
③当F与C点重合时,过O点作OG⊥OC,交BC于G点,
OF=OC=AC===.
故答案为2,2a,
15.
【分析】如图,设正方形网格的边长为1,根据勾股定理求出△EFD、△ABC的边长,运用三边对应成比例,则两个三角形相似这一判定定理证明△EDF∽△BAC,即可解决问题.
【详解】:如图,设正方形网格的边长为1,由勾股定理得:
DE2=22+22,EF2=22+42,
∴DE=2,EF=2;
同理可求:AC=,BC=,
∵DF=2,AB=2,
∴,
∴△FDE∽△CAB,
∴S△CAB:S△FDE= AC2:DF2=,
故答案为.
【点睛】此题考查相似三角形的判定及其性质定理的应用问题;应牢固掌握有关定理,这是灵活运用解题的关键.
16.
【分析】连接BC,求得BC=5,证明△ABC∽△EAB,根据相似性质即可求出BE.
【详解】解:如图,连接.
在中,根据勾股定理,得
是直径,
.
是的切线,
即
,
故答案为:
【点睛】(1)见直径,想半径或想圆周角为直角;
(2)见切线想做过切点的直径,构造直角;
(3)求线段的长度在几何图形中一般选择勾股定理、相似、或三角函数来求解.
17.-12
【分析】设点A坐标为(a,b),则,连接,易证,.然后构造相似三角形,过点A作轴,垂足为E,过点C作轴,垂足为D,可证.从而得到,.设点C坐标为(x,y),从而有,即.
【详解】解:如图,设点A坐标为(a,b),点C坐标为(x,y),连接、,过点A作轴,垂足为E,过点C作轴,垂足为D,
∵点A在双曲线上,点C在双曲线上,
∴,,
∵线段绕点B逆时针旋转,得到线段,
∴,,
∴为等边三角形,
∵点A与点B关于原点对称,
∴,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,,
∴,
∴.
故答案为:
【点睛】本题考查的是反比例函数综合题,涉及到等边三角形的判定和性质、勾股定理的应用、反比例函数的性质和相似三角形的判定与性质等知识点,有一定的难度.通过作辅助线构造相似三角形是解答本题的关键.
18.甲同学的加工方法符合要求
【分析】
设正方形的边长为x,然后找到合适的相似三角形建立线段之间的比例关系,求得x的值.
【详解】设正方形的边长为 .
甲的方法:由 ,得 ,
即 ,解得 ;
乙的方法:过点 作 边上的高线,分别交 , 于点 ,(如下图),
由勾股定理得:.
,
∴.则.
由 ,得 ,
即 ,解得 .
因为 ,
所以甲同学的加工方法符合要求.
【点睛】本题考查了直角三角形、正方形、相似三角形的性质及应用,解题的关键是找到恰当的相似三角形来求得正方形的边长.
19.(1)见解析
(2)3
【分析】本题考查作图-相似变换,相似三角形的判定与性质.
(1)由可得,,根据作一个角等于已知角的作图方法作,交于点N,则点N即为所求.
(2)由相似三角形的性质可得,由中点的定义可得,则,即可得出答案.
【详解】(1)解:∵,
∴.
如图,作,交于点N,则点N即为所求.
(2)解:∵,
∴,
∵点M为的中点,
∴,
∴,
,
.
20.
【分析】此题考查相似三角形的应用,关键是根据相似三角形的判定和性质得出边的大小解答.
证明得到对应边成比例,列方程解决即可.
【详解】解:设米,米,
∵,
,
,
,,
,
,
,
,
,
,
,
,
,
经检验,是原方程的解,
,
,
经检验,是原方程的解,
答:飞虹塔的高度为米.
21.(1);;相似三角形的对应边成比例
(2)150牛顿
【分析】本题主要考查了相似三角形的性质与判定,作辅助线构造相似三角形是解题的关键.
(1)依据相似三角形的对应边成比例进行推导即可;
(2)过点O作,交延长线于点E,延长交的延长线于点F,先证得,推出,再利用“动力动力臂阻力阻力臂”代入进行求解即可.
【详解】(1)解:∵,
∴,
∵,
∴,
运用到的几何知识是相似三角形对应边成比例,
故答案为:;;相似三角形对应边成比例.
(2)解:如图,过点O作,交延长线于点E,延长交的延长线于点F,
∵,
∴,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
即,
∴,
即(牛顿),
答:的大小为150牛顿.
22.云龙山塔的高度是24米.
【分析】本题考查了相似三角形的应用.先证明,,利用其性质可得,,即可得,,求解即可.
【详解】解:∵,,,
∴
又∵,,
∴,,
∴,,
∵,,,,
∴,,
∴,,
∴云龙山塔的高度是24米.
23.(1)见解析
(2)见解析
【分析】(1)根据两边对应成比例,且夹角相等的两个三角形相似即可证明;
(2)利用等腰三角形的性质及相似三角形的性质即可证明.
【详解】(1)证明:∵,
∴,
∵,
∴;
(2)证明:∵,
∴(等边对等角),
∵(已证)
∴(相似三角形的对应角相等)
∴(角的和差定义)
∴(三角形内角和定理),
∴(等量代换)
∴(等角对等边).
【点睛】本题考查相似三角形的判定和性质,等腰三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
24.(1)证明见解析;(2)60°;(3)6.
【分析】(1)先判断出∠BAC=∠ACB,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(2)先判断出∠BAD=∠ACE=120°,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(3)先求出AC=12,再判断出△ADF∽△ACM,即可得出结论.
【详解】解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
在△ABD和△CAE中,,
∴△ABD≌△CAE,
∴BD=AE,
(2)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
∴∠BAD=∠ACE=120°
在△ABD和△CAE中,,
∴△ABD≌△CAE,
∴∠ADB=∠CEA,
∴∠BFE=∠ADB+∠DAF=∠AEC+∠CAE=∠ACB=60°;
(3)∵CM∥BD,
∴△ADF∽△ACM,
∴ ,
∵AF:AM=2:4=1:2,
∴AD=AC,
∵△ABC是等边三角形,
∴AC=BC=12,
∴AD=6,
∵AD=CE,
∴CE=AD=6.
【点睛】此题是三角形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,解本题的关键是判断出两三角形全等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
27.2相似三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,,,将沿折叠,使点C落在边上处,并且,则的长是( )
A. B. C. D.
2.如图所示的网格是正方形网格,A,B,C,D是网格线交点,AC与BD相交于点O,则的面积与的面积的比为( )
A.1:2 B. C.1:4 D.
3.如图,点D,E分别在△ABC的两边上,,若,,,则为( )
A.13 B. C.14 D.15
4.如图,在△ABC中,DE∥BC,若DE=2,BC=6,则=( )
A. B. C. D.
5.如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是
A.b2=ac B.b2=ce C.be=ac D.bd=ae
6.如图,已知与都是等边三角形,点、、在同一直线上,连结交于点,连结分别与、交于点、,下列结论不一定成立的是( )
A. B. C. D.
7.如图,已知.若,则的度数为( )
A. B. C. D.
8.如图,铁道口的栏杆短臂OA长1m,长臂OB长8m.当短臂外端A下降0.5m时,长臂外端B升高( )
A.2m B.4m C.4.5m D.8m
9.如图,在平行四边形中,是的中点,和交于点,设△的面积为,△ 的面积为,则下列结论中正确的是( )
A. B.
C. D.
10.如图,点D、E分别是的边、的中点,则( )
A.1:2 B.3:1 C.1:3 D.1:4
11.如图,是线段上一动点,分别以为边向上作正方形、,连接交于.已知,设,记的面积为,记的面积为.则与的函数关系为( )
A.正比例函数关系 B.一次函数关系 C.反比例函数关系 D.二次函数关系
12.如图,矩形中,,以点B为圆心,适当长为半径画弧,分别交,于点E,F,再分别以点E,F,为圆心,大于长为半径画弧交于点P,作射线,过点C作的垂线分别交于点M,N,则的长为( )
A.1 B. C. D.2
二、填空题
13.如图,在中,D,E分别是边,的中点,,相交于点F,则 .
14.矩形ABCD的对角线AC与BD相交于点O,AD=2AB=4,现有一直角三角板的直角顶点放在点O处,直角三角板的两边与矩形ABCD的边交于点E,F,如果OE=a,用a的代数式表示出所有可能的OF的值
15.如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么S△CAB:S△FDE的值为 .
16.如图,已知是的直径, 是的弦,过点作的切线,与的延长线交于点作交直线于点.若则 .
17.如图,点A是双曲线上一个动点,连接并延长,交双曲线另一支于点B,把线段绕点B逆时针旋转,得到线段,若点C在另一双曲线上,则 .
三、解答题
18.如图,一块直角三角形木板的两直角边,的长分别为,.要把它加工成面积最大的正方形桌面,甲、乙两位同学的加工方法分别如图①,图②所示,请你用学过的知识说明哪位同学的加工方法符合要求(加工损耗忽略不计,计算结果中的分数可以保留)
19.已知中,,点为的中点.
(1)在线段上求作一点,使(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下求线段的长.
20.近期《黑神话:悟空》正式在全球上线,迅速吸引了全球游戏爱好者的目光,《黑神话:悟空》游戏中选取的27处山西极具代表性的古建筑,不仅展示了山西深厚的文化底蕴,也为当地文旅产业带来新的发展机遇,更为山西的文化元素提供了一个面向全球游戏玩家群体的数字化传播窗口.飞虹塔是山西省非常有名的一座塔楼,这座塔的位置位于山西省洪洞县广胜寺景区.某实践小组欲测量飞虹塔的高度,过程见下表.根据表格信息,求飞虹塔的大致高度.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
测量步骤 步骤1:把长为2米的标杆垂直立于地面点D处,塔尖点A和标杆顶端C确定的直线交水平于点Q,测得米; 步骤2:将标杆沿着的方向平移到点F处,塔尖点A和标杆顶端E确定的直线交直线于点P,测得米,米;(以上数据均为近似值)
21.课题:《杠杠原理与相似三角形》
杠杆原理:也称为“杠杆平衡条件”:杠杆原理是几何学在物理学的体现.
相关概念:
支点:杠杆绕着转动的固定点;
动力:使杠杆转动的力;
阻力:阻碍杠杆转动的力;
动力臂:从支点到动力作用线的距离;
阻力臂:从支点到阻力作用线的距离.
基本模型:当一个力通过一个支点施加在杠杆上时,通过作图,可以观察到两个相似的三角形
如图,因为,,
所以, 则有 ①
又因为(消耗的功一致),可得 ,所以
可得②______(为阻力的反作用力).
即,动力动力臂阻力阻力臂.
得出结论:要使杠杆平衡,作用在杠杆上的两个力矩(力与力臂的乘积)大小必须相等
(1)补全①、②所缺的内容,课题证明杠杆原理过程中运用到的几何知识是
(2)如图,小明用实心钢管制作了一个自带支点杠杆A-O-B,O为支点,,,,,方向上因撑起一物体产生450牛顿(国际单位制中,力的单位)的阻力,方向上施加一个力使杠杆平衡,.
请利用“动力臂”,“阻力臂”与“支点”概念构造相似三角形 ,并运用“杠杆原理”相关知识,求出的大小.
22.某数学小组为了测量云龙山上宝塔的高度,利用休息时间进行了实地测量:如图2,首先把长为2米的标杆垂直立于地面上的点处,当塔尖、标杆顶端与地面上的点在同一直线上时,米;再将标杆沿方向平移11米至点处(即米,米),当塔尖、标杆顶端与地面上的点在同一直线上时,米,已知,,,点、、、、在同一水平直线上,请你帮助这个数学小组求出云龙山上宝塔的高度.
23.如图,在中,
(1)求证:;
(2)试证明;(要求:证明过程注明理由)
24.已知△ABC是等边三角形,在直线AC、直线BC上分别取点D和点且AD=CE,直线BD、AE相交于点F.
(1)如图1所示,当点D、点E分别在线段CA、BC上时,求证:BD=AE;
(2)如图2所示,当点D、点E分别在CA、BC的延长线时,求∠BFE的度数;
(3)如图3所示,在(2)的条件下,过点C作CM∥BD,交EF于点M,若DF:AF:AM=1:2:4,BC=12,求CE的长度.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D A C D B B C
题号 11 12
答案 B A
1.B
【分析】根据勾股定理就可以求出AC的值,再根据轴对称的性质就可以得出,由得出就可以得出就可以求出结论.
【详解】解:∵,由勾股定理,得.
∵与关于成轴对称,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
故选:B.
【点睛】本题考查了勾股定理的运用,轴对称的性质的运用,相似三角形的判定及性质的运用,解答时运用轴对称的性质求解是关键.
2.C
【分析】设小方格的边长为1,根据等腰直角三角形和勾股定理求出AB和CD的长,再根据
得到 ,然后利用相似三角形的性质来求解.
【详解】解:如下图,
设小方格的边长为1,
∵、分别是边长为1和2的等腰直角三角形,
∴,,.
∵,
∴,
∴.
又∵ ,
∴,
∴,
∴.
故选:C.
【点睛】本题考查相似三角形面积比与相似比的关系,关键是判断两三角形相似,确定其相似比.
3.D
【分析】本题考查了相似三角形的性质和判定,平行线的判定的应用,关键是推出.
首先证明出,然后得到,然后代数求解即可.
【详解】解:∵,
∴,
∴,即,
解得:,
故选D.
4.D
【分析】由DE∥BC知△ADE∽△ABC,然后根据相似比求解.
【详解】解:∵DE∥BC
∴△ADE∽△ABC.
又因为DE=2,BC=6,可得相似比为1:3.
即==.
故选D.
【点睛】本题主要是先证明两三角形相似,再根据已给的线段求相似比即可.
5.A
【详解】试题分析:∵CD∥AB,∴∠CDB=∠DBA.
又∵∠C=∠BDA=90°,∴△CDB∽△DBA.∴,即.
∴A、b2=ac,成立,故本选项正确;
B、b2=ac,不是b2=ce,故本选项错误;
C、be=ad,不是be=ac,故本选项错误;
D、bd=ac,不是bd=ae,故本选项错误.
故选A.
6.C
【分析】根据等边三角形的性质及相似三角形的判定可进行求解.
【详解】解:∵与都是等边三角形,
∴,
∴,
∴,即,且相似比为1,
∵,
∴,
∴,,
∴不一定成立;
故选C.
【点睛】本题主要考查相似三角形的性质与判定及等边三角形的性质,熟练掌握相似三角形的性质与判定及等边三角形的性质是解题的关键.
7.D
【分析】本题主要考查了相似三角形的性质,三角形的内角和定理,解答的关键是结合图形分析清楚各角的关系.
由相似可得,利用三角形的外角性质可求得,从而可求的度数.
【详解】解:∵,
,
故选:D.
8.B
【详解】设长臂外端B升高xm,根据三角形相似得,∴x=4,故选B.
9.B
【详解】∵ ∥,∴ △∽△.又∵ 是的中点,∴ ,
∴ :=,即.
10.C
【分析】本题考查了相似三角形的判定与性质,中位线的性质,现根据点D、E分别是的边、的中点,得是的中位线,即,且,即可作答.
【详解】解:∵点D、E分别是的边、的中点,
∴是的中位线,即,
∴,
则,
故,
那么,
故选:C.
11.B
【分析】四边形、是正方形,,设,可用含的式子表示,根据,可得,设,则,可求出,由此即可求解.
【详解】解:四边形、是正方形,,设,
∴,
∴,
∴,
设,则,
∵,
∴,
∴,即,解得,,
∴,
∴,
∴是关于的一次函数,
故选:.
【点睛】本题主要考查运用几何面积表示函数关系,掌握几何面积的计算方法是解题的关键.
12.A
【分析】先根据矩形的性质以及勾股定理得到,,,,再由作图过程知平分,进而证明,,则,再证明,即可求得的长.
【详解】矩形中,,,
,,,
,
由作图过程知平分,则,
,
,
,
,
,
,
,
,
,即,
,
故选:A.
【点睛】本题考查矩形的性质、勾股定理、角平分线的尺规作图、全等三角形的判定与性质、相似三角形的判定与性质等知识,熟练掌握相似三角形的判定与性质以及判断出平分是解答的关键.
13.
【分析】连接,利用三角形的中位线定理,得到,得到,得到,进一步求解即可.
【详解】解:连接,
∵D,E分别是边,的中点,
则:,
∴,
∴,
∴;
故答案为:.
【点睛】本题考查相似三角形的判定和性质.解题的关键是添加辅助线,利用三角形的中位线定理,证明三角形相似.
14.
【详解】解:①当F为CD的中点时,OE=FC=FD=a=1,
∵O为BD的中点,∴OF∥BC,
∴△DFO∽△DCB,则=,OF=2,
②当F不是CD的中点时,作OM⊥BC,ON⊥CD,垂足分别为M、N,
∵∠MON=∠EOF=90°,
∴∠MOE=∠NOF,
∴△OME∽△ONF,==2,OF=2a,
③当F与C点重合时,过O点作OG⊥OC,交BC于G点,
OF=OC=AC===.
故答案为2,2a,
15.
【分析】如图,设正方形网格的边长为1,根据勾股定理求出△EFD、△ABC的边长,运用三边对应成比例,则两个三角形相似这一判定定理证明△EDF∽△BAC,即可解决问题.
【详解】:如图,设正方形网格的边长为1,由勾股定理得:
DE2=22+22,EF2=22+42,
∴DE=2,EF=2;
同理可求:AC=,BC=,
∵DF=2,AB=2,
∴,
∴△FDE∽△CAB,
∴S△CAB:S△FDE= AC2:DF2=,
故答案为.
【点睛】此题考查相似三角形的判定及其性质定理的应用问题;应牢固掌握有关定理,这是灵活运用解题的关键.
16.
【分析】连接BC,求得BC=5,证明△ABC∽△EAB,根据相似性质即可求出BE.
【详解】解:如图,连接.
在中,根据勾股定理,得
是直径,
.
是的切线,
即
,
故答案为:
【点睛】(1)见直径,想半径或想圆周角为直角;
(2)见切线想做过切点的直径,构造直角;
(3)求线段的长度在几何图形中一般选择勾股定理、相似、或三角函数来求解.
17.-12
【分析】设点A坐标为(a,b),则,连接,易证,.然后构造相似三角形,过点A作轴,垂足为E,过点C作轴,垂足为D,可证.从而得到,.设点C坐标为(x,y),从而有,即.
【详解】解:如图,设点A坐标为(a,b),点C坐标为(x,y),连接、,过点A作轴,垂足为E,过点C作轴,垂足为D,
∵点A在双曲线上,点C在双曲线上,
∴,,
∵线段绕点B逆时针旋转,得到线段,
∴,,
∴为等边三角形,
∵点A与点B关于原点对称,
∴,
∴,,
∴,
∴,
∵,
∴,
∴,
∴,
∴,,
∴,
∴.
故答案为:
【点睛】本题考查的是反比例函数综合题,涉及到等边三角形的判定和性质、勾股定理的应用、反比例函数的性质和相似三角形的判定与性质等知识点,有一定的难度.通过作辅助线构造相似三角形是解答本题的关键.
18.甲同学的加工方法符合要求
【分析】
设正方形的边长为x,然后找到合适的相似三角形建立线段之间的比例关系,求得x的值.
【详解】设正方形的边长为 .
甲的方法:由 ,得 ,
即 ,解得 ;
乙的方法:过点 作 边上的高线,分别交 , 于点 ,(如下图),
由勾股定理得:.
,
∴.则.
由 ,得 ,
即 ,解得 .
因为 ,
所以甲同学的加工方法符合要求.
【点睛】本题考查了直角三角形、正方形、相似三角形的性质及应用,解题的关键是找到恰当的相似三角形来求得正方形的边长.
19.(1)见解析
(2)3
【分析】本题考查作图-相似变换,相似三角形的判定与性质.
(1)由可得,,根据作一个角等于已知角的作图方法作,交于点N,则点N即为所求.
(2)由相似三角形的性质可得,由中点的定义可得,则,即可得出答案.
【详解】(1)解:∵,
∴.
如图,作,交于点N,则点N即为所求.
(2)解:∵,
∴,
∵点M为的中点,
∴,
∴,
,
.
20.
【分析】此题考查相似三角形的应用,关键是根据相似三角形的判定和性质得出边的大小解答.
证明得到对应边成比例,列方程解决即可.
【详解】解:设米,米,
∵,
,
,
,,
,
,
,
,
,
,
,
,
,
经检验,是原方程的解,
,
,
经检验,是原方程的解,
答:飞虹塔的高度为米.
21.(1);;相似三角形的对应边成比例
(2)150牛顿
【分析】本题主要考查了相似三角形的性质与判定,作辅助线构造相似三角形是解题的关键.
(1)依据相似三角形的对应边成比例进行推导即可;
(2)过点O作,交延长线于点E,延长交的延长线于点F,先证得,推出,再利用“动力动力臂阻力阻力臂”代入进行求解即可.
【详解】(1)解:∵,
∴,
∵,
∴,
运用到的几何知识是相似三角形对应边成比例,
故答案为:;;相似三角形对应边成比例.
(2)解:如图,过点O作,交延长线于点E,延长交的延长线于点F,
∵,
∴,
∴,
∵,
∴,
又∵,
∴,
∴,
∴,
即,
∴,
即(牛顿),
答:的大小为150牛顿.
22.云龙山塔的高度是24米.
【分析】本题考查了相似三角形的应用.先证明,,利用其性质可得,,即可得,,求解即可.
【详解】解:∵,,,
∴
又∵,,
∴,,
∴,,
∵,,,,
∴,,
∴,,
∴云龙山塔的高度是24米.
23.(1)见解析
(2)见解析
【分析】(1)根据两边对应成比例,且夹角相等的两个三角形相似即可证明;
(2)利用等腰三角形的性质及相似三角形的性质即可证明.
【详解】(1)证明:∵,
∴,
∵,
∴;
(2)证明:∵,
∴(等边对等角),
∵(已证)
∴(相似三角形的对应角相等)
∴(角的和差定义)
∴(三角形内角和定理),
∴(等量代换)
∴(等角对等边).
【点睛】本题考查相似三角形的判定和性质,等腰三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
24.(1)证明见解析;(2)60°;(3)6.
【分析】(1)先判断出∠BAC=∠ACB,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(2)先判断出∠BAD=∠ACE=120°,进而用SAS即可判断出△ABD≌△CAE,即可得出结论;
(3)先求出AC=12,再判断出△ADF∽△ACM,即可得出结论.
【详解】解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
在△ABD和△CAE中,,
∴△ABD≌△CAE,
∴BD=AE,
(2)∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AB=AC,
∴∠BAD=∠ACE=120°
在△ABD和△CAE中,,
∴△ABD≌△CAE,
∴∠ADB=∠CEA,
∴∠BFE=∠ADB+∠DAF=∠AEC+∠CAE=∠ACB=60°;
(3)∵CM∥BD,
∴△ADF∽△ACM,
∴ ,
∵AF:AM=2:4=1:2,
∴AD=AC,
∵△ABC是等边三角形,
∴AC=BC=12,
∴AD=6,
∵AD=CE,
∴CE=AD=6.
【点睛】此题是三角形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,解本题的关键是判断出两三角形全等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
