28.1锐角三角函数同步练习(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
28.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在菱形中,,E是上一点,连接,将沿AE翻折,使点B落在点F处,连接.若,则的值为( )
A. B. C. D.
2.关于x的一元二次方程x2﹣4sinα x+2=0有两个等根,则锐角α的度数是( )
A.30° B.45° C.60° D.90°
3.如图,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点.已知坡角为20°,山高千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是( )
A. B. C. D.
4.如果∠A是锐角,且sinA=,那么cos(90°-∠A)等于( )
A. B. C. D.
5.在中,,,,那么的正切值是( )
A. B.7 C. D.
6.如图,在中,,,,则
A. B. C. D.
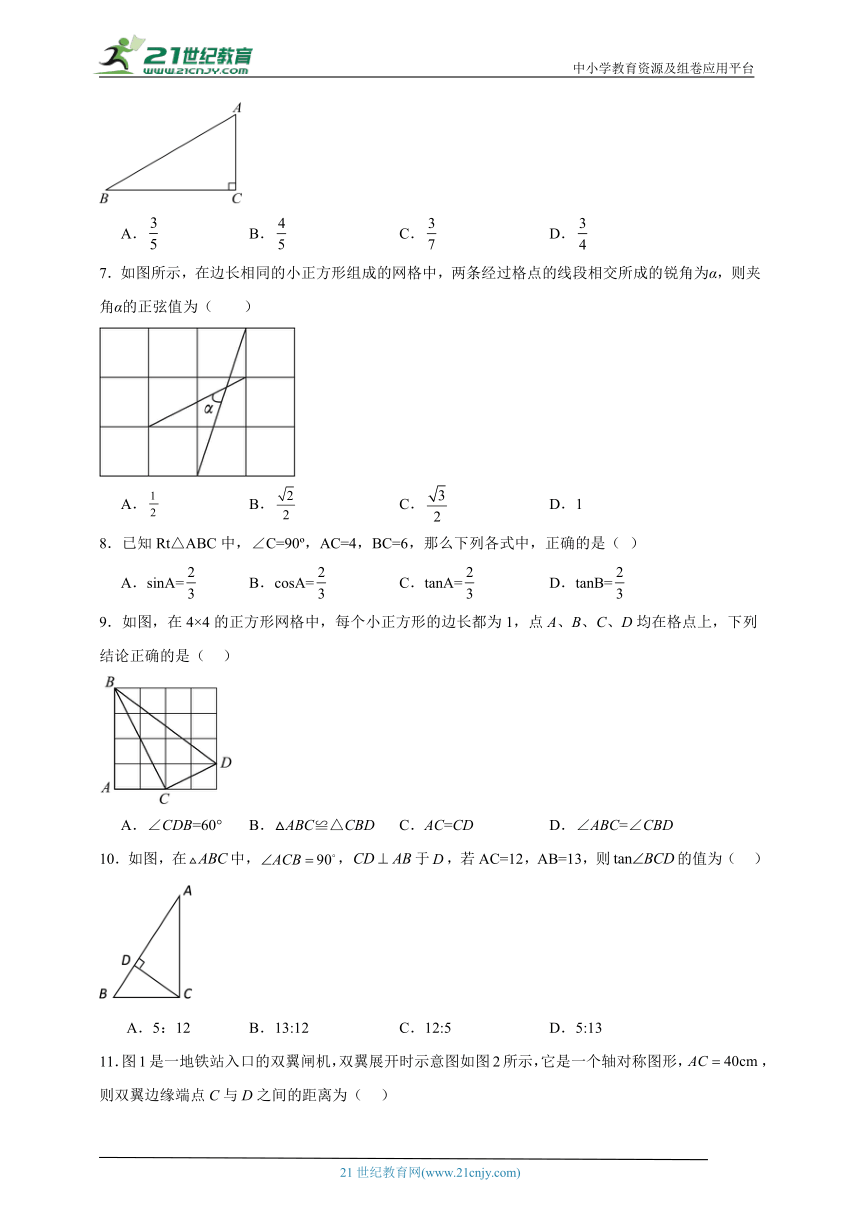
7.如图所示,在边长相同的小正方形组成的网格中,两条经过格点的线段相交所成的锐角为α,则夹角α的正弦值为( )
A. B. C. D.1
8.已知Rt△ABC中,∠C=90 ,AC=4,BC=6,那么下列各式中,正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
9.如图,在4×4的正方形网格中,每个小正方形的边长都为1,点A、B、C、D均在格点上,下列结论正确的是( )
A.∠CDB=60° B.△ABC≌△CBD C.AC=CD D.∠ABC=∠CBD
10.如图,在中,,于,若AC=12,AB=13,则的值为( )
A.5:12 B.13:12 C.12:5 D.5:13
11.图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,,则双翼边缘端点C与D之间的距离为( )
A. B.
C. D.
12.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C度数是( )
A.75° B.90° C.105° D.120°
二、填空题
13.如图所示的网格是正方形网格,则∠AOB ∠COD.(填“>”,“=”或“<”)
14.如图,已知为斜边上的高,且,,那么等于 cm.
15.计算: .
16.若,则锐角 锐角(填、或).
17.在中,,,,则的值是 .
三、解答题
18.计算:.
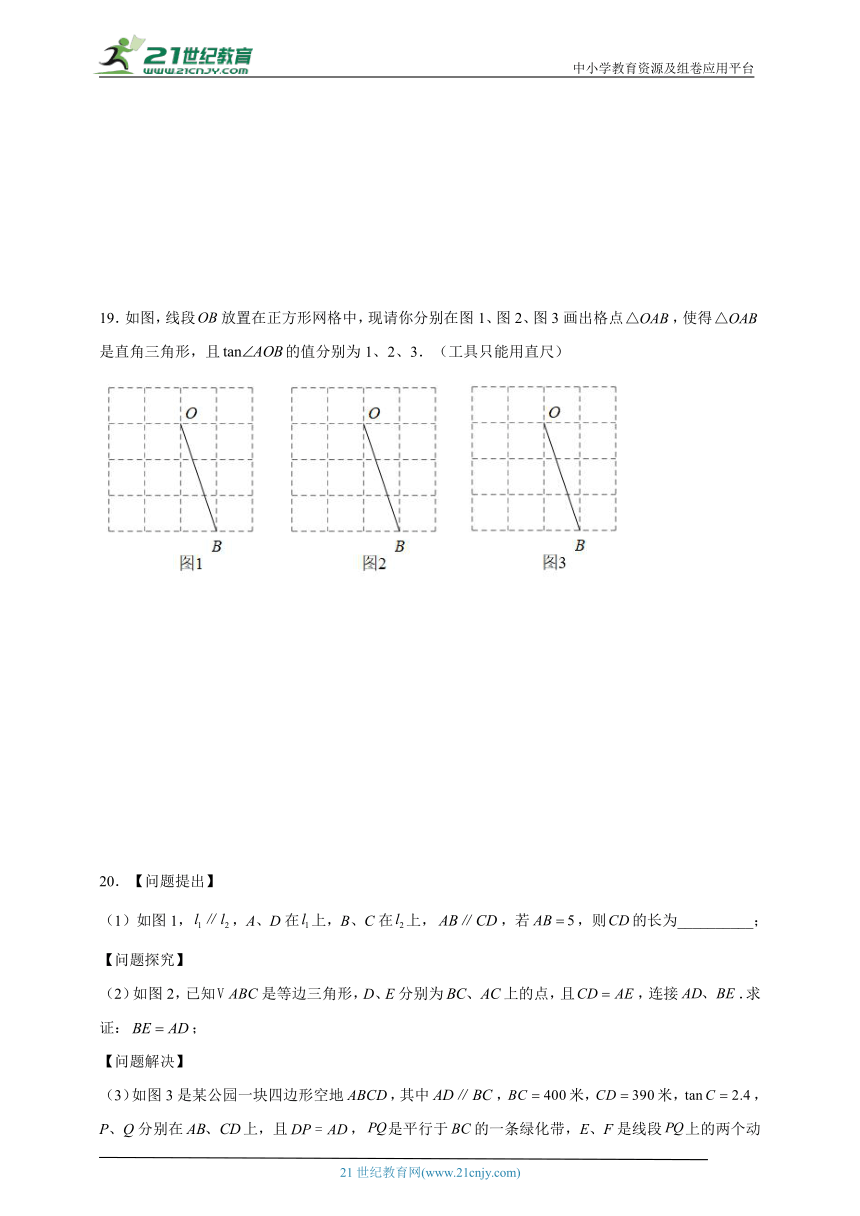
19.如图,线段放置在正方形网格中,现请你分别在图1、图2、图3画出格点,使得是直角三角形,且的值分别为1、2、3.(工具只能用直尺)
20.【问题提出】
(1)如图1,,A、D在上,B、C在上,,若,则的长为__________;
【问题探究】
(2)如图2,已知是等边三角形,D、E分别为上的点,且,连接.求证:;
【问题解决】
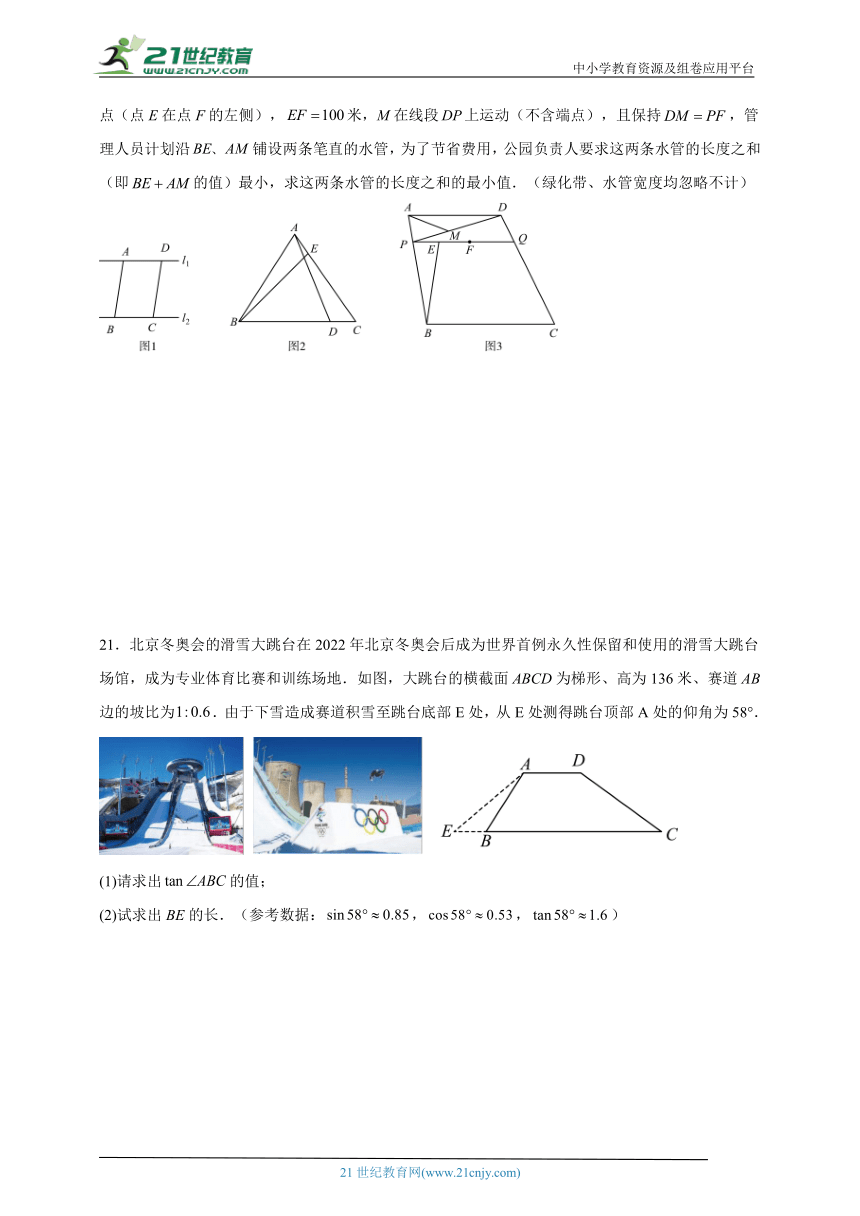
(3)如图3是某公园一块四边形空地,其中,米,米,,P、Q分别在上,且,是平行于的一条绿化带,E、F是线段上的两个动点(点E在点F的左侧),米,M在线段上运动(不含端点),且保持,管理人员计划沿铺设两条笔直的水管,为了节省费用,公园负责人要求这两条水管的长度之和(即的值)最小,求这两条水管的长度之和的最小值.(绿化带、水管宽度均忽略不计)
21.北京冬奥会的滑雪大跳台在2022年北京冬奥会后成为世界首例永久性保留和使用的滑雪大跳台场馆,成为专业体育比赛和训练场地.如图,大跳台的横截面ABCD为梯形、高为136米、赛道AB边的坡比为.由于下雪造成赛道积雪至跳台底部E处,从E处测得跳台顶部A处的仰角为58°.
(1)请求出的值;
(2)试求出BE的长.(参考数据:,,)
22.问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
23.已知:如图,,、是上的两点,.
(1)求证:;
(2)锐角的正切函数值随角度的增大而________.
24.如图,在中,是弦,过点O作与交于点C,在的延长线取点D,使.
(1)求证:是的切线;
(2)若,,求的半径长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A A A B D D A
题号 11 12
答案 D C
1.D
【分析】设与的交点为,,根据折叠的性质,可得,根据,可得为等腰直角三角形,从而得到,利用直角三角形的性质即可求解.
【详解】解:设与的交点为,设,则
由菱形的性质可得,,
由折叠的性质可得,,
则,
∴为等腰直角三角形,,
∴,即,
在中,,,
∴,
,
,
故选:D
【点睛】此题考查了菱形的性质,折叠的性质,解直角三角形,解题的关键是熟练掌握相关基本性质,确定.
2.B
【分析】先利用判别式的意义得到△=16sin2α-4×2=0,然后求出α的正弦值,再利用特殊角的三角函数值确定锐角α的度数.
【详解】根据题意得△=16sin2α-4×2=0,
所以sinα=,
所以锐角α=45°.
故选B.
【点睛】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了特殊角的三角函数值.
3.A
【分析】在△ABC中,通过解直角三角形可得出sinA= ,则,即可得出结论.
【详解】解:在△ABC中,sinA=sin20°= ,
∴,
∴按键顺序为:2÷sin20=
故选:A.
【点睛】本题主要考查解直角三角形的应用-坡度坡角问题以及计算器,熟练应用计算器是解题关键.
4.A
【分析】根据互为余角三角函数关系,解答即可.
【详解】解:∵α为锐角,sinα=,
∴cos(90°-α)=sinα=,
故选A.
【点睛】本题主要考查了互为余角的三角函数值,解决本题的关键是要熟记三角函数关系式.
5.A
【分析】本题主要考查了求角的正切值,熟知在直角三角形一个角的正切值等于该角的对边比上另一条直角边是解题的关键.
【详解】解:∵在中,,,,
∴,
故选A.
6.A
【分析】先利用勾股定理求出斜边AB,再求出sinB即可.
【详解】∵在中,,,,
∴,
∴.
故答案为A.
【点睛】本题考查的知识点是锐角三角函数的定义,解题关键是熟记三角函数的定义.
7.B
【分析】如图,设AB与CD交于点E,过点C作CF∥AB,连接DF,可得,设小正方形的边长为1,然后根据勾股定理及逆定理可得△CDF为等腰直角三角形,从而得到∠C=45°,即可求解.
【详解】解:如图,设AB与CD交于点E,过点C作CF∥AB,连接DF,
∵CF∥AB,
∴,
设小正方形的边长为1,
根据勾股定理得:,
,
,
∴,DF=CF,
∴△CDF为等腰直角三角形,
∴∠C=45°,
∴,
∴夹角α的正弦值为.
故选:B
【点睛】本题主要考查了勾股定理及其逆定理,锐角三角函数,根据题意,做适当辅助线构造出直角三角形是解题的关键.
8.D
【分析】本题可以利用锐角三角函数的定义以及勾股定理分别求解,再进行判断即可.
【详解】∵∠C=90°,BC=6,AC=4,
∴AB=,
A、sinA=,故此选项错误;
B、cosA=,故此选项错误;
C、tanA=,故此选项错误;
D、tanB=,故此选项正确.
故选:D.
【点睛】此题主要考查了锐角三角函数的定义以及勾股定理,熟练应用锐角三角函数的定义是解决问题的关键.
9.D
【分析】根据勾股定理可以得到 BC 、 CD 、 BD 的长,再根据勾股定理的逆定理可以得到△BCD 的形状,根据图形,很容易判断△ABC≌△CBD和AC = CD 不成立;再根据锐角三角函数可以得到∠ABC 和∠CBD的关系.
【详解】由图可得,
BC =,
CD =,
BD =,
∴BC2 + CD2 ==BD2,
∴△BCD 是直角三角形,
∴,
∵,
∴∠CDB≠60°,故选项A错误,不符合题意;
由图可知,显然△ABC 和△CBD 不全等,故选项 B错误,不符合题意;
∵AC =2,CD =,
∴AC ≠ CD ,故选项 C 错误,不符合题意;
∵,
∴∠ABC =∠CBD ,故选项 D 正确.
【点睛】本题考查相似三角形的判与性质、勾股定理与勾股定理的逆定理、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
10.A
【分析】证明∠BCD=∠A,求tanA即可.根据三角函数的定义求解.
【详解】由勾股定理知,c2=a2+b2
∴BC=.
根据同角的余角相等,∠BCD=∠A.
∴tan∠BCD=tan∠A=.
故选A.
【点睛】本题利用了等角进行转换求解,考查三角函数的定义.
11.D
【分析】作辅助线如图,由题意可得,,解直角三角形求出,然后根据即可得出答案.
【详解】解:如图,作直线,交双翼闸机于点E、F,则,
由题意可得,,
在直角三角形中,∵,
∴,
∴;
故选:D.
【点睛】本题考查了解直角三角形的应用,正确理解题意、熟练掌握锐角三角函数的知识是解题的关键.
12.C
【详解】解:由题意得:|sinA﹣|=0,(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=, =cosB,
∴∠A=45°,∠B=30°,
∴∠C=180°﹣∠A﹣∠B=105°.
故选C.
【点睛】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握二次根式、绝对值、非负数等考点的运算.
13.=
【分析】根据tan∠AOB与tan∠COD的大小比较即可求解.
【详解】解:根据题意可知tan∠AOB=2,tan∠COD=2,
∴∠AOB=∠COD,
故答案为=.
【点睛】本题考查了锐角三角函数的增减性,构建直角三角形求角的三角函数值进行判断,熟练掌握锐角三角函数的增减性是关键.
14.
【分析】由题意易得,则有,然后可得,进而根据计算求解即可.
【详解】解:∵AD⊥BC,
∴,
在中,由勾股定理得,
∴,
∵∠CAB=90°,
∴;
故答案为:.
【点睛】本题考查了解直角三角形余弦,勾股定理等知识.熟练掌握余弦的求解是解题的关键.
15.-2
【分析】先根据二次根式、负整数指数幂、特殊三角函数值、0指数幂进行化简,再计算即可.
【详解】原式=.
故答案为:-2.
【点睛】本题考查实数的混合运算,解题的关键是根据二次根式、负整数指数幂、特殊三角函数值、0指数幂进行化简.
16.
【分析】本题考查了正弦的定义,根据在锐角范围内,正弦的函数值随着角度的增大而增大即可得出答案,熟练掌握相关知识点是解此题的关键.
【详解】解:∵在锐角范围内,正弦的函数值随着角度的增大而增大,
∴若,则锐角锐角,
故答案为:.
17.
【分析】先由勾股定理求解,再由锐角的正弦的定义可得:,从而可得答案.
【详解】解:如图, ,,,
故答案为:
【点睛】本题考查的是锐角的正弦的定义,勾股定理的应用,掌握锐角的正弦的定义是解题的关键.
18.
【分析】本题考查了特殊角三角函数值的混合运算,注意计算的准确性即可.
【详解】解:原式
.
19.见解析
【分析】根据勾股定理以及正切值对应边关系即可得到结果
【详解】解:如图所示:,
如图所示:,
如图所示:,
【点睛】本题考查了应用与设计作图、锐角三角函数关系及勾股定理,正确构造直角三角形是解决问题的关键
20.(1)5(2)见解析(3)390米
【分析】(1)首先根据条件证明四边形是平行四边形,再根据平行四边形对边相等可得到即可;
(2)根据证明,进而解答即可;
(3)连接,过点D作于,根据米,求出米,米,证明,可得,在上截取米,连接,可得四边形是平行四边形,,则,根据,可得的最小值为的长,利用勾股定理即可求解.
【详解】解:(1)∵,A、D在上,B、C在上,
∴,
∵
∴四边形是平行四边形,
∴
故答案为:5;
(2)证明:∵为等边三角形,
∴,
在与中,
,
∴,
∴;
(3)解:连接,过点D作于H,
∵,
∴,
设,则,
∵米,,
∴,
解得(负值舍去),
∴米,米,
∵,
∴,
∴,
∵,
∴,
∴,
在上截取米,连接,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴的最小值为的长,
∵(米),
∴(米),
∴这两条水管的长度之和的最小值为390米.
【点睛】本题主要考查平行四边形的判定和性质,等边三角形的性质,全等三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题.
21.(1)
(2)3.4米
【分析】(1)根据坡比的概念即可求得的正切值;
(2)过点A作交CE于点F,根据题意得出,,然后分别利用和的正切求出、的值,最后根据线段的和差即可得出答案.
【详解】(1)赛道AB边的坡比为
(2)过点A作交CE于点F
则,
在中,
∴
在中,
∴
∴
答:BE长度约为3.4米.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答问题的关键.
22.(1)5;(2)18;(3)(3-9)km.
【详解】【分析】(1)如图(1),设外接圆的圆心为O,连接OA, OB,根据已知条件可得△AOB是等边三角形,由此即可得半径;
(2)如图(2)所示,连接MO并延长交⊙O于N,连接OP,显然,MN即为MP的最大值,根据垂径定理求得OM的长即可求得MN的最大值;
(3) 如图(3)所示,假设P点即为所求点,分别作出点P关于AB、AC的对称点P 、P"连接PP 、P E,PE,P"F,PF,PP",则P P"即为最短距离,其长度取决于PA的长度, 根据题意正确画出图形,得到点P的位置,根据等边三角形、勾股定理等进行求解即可得PE+EF+FP的最小值.
【详解】(1)如图(1),设外接圆的圆心为O,连接OA, OB,
∵O是等腰三角形ABC的外心,AB=AC,
∴∠BAO=∠OAC=∠BAC==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OB=AB=5,
故答案为5;
(2)如图(2)所示,连接MO并延长交⊙O于N,连接OP,
显然,MP≤OM+OP=OM+ON=MN,ON=13,OM==5,MN=18,
∴PM的最大值为18;
(3) 如图(3)所示,假设P点即为所求点,分别作出点P关于AB、AC的对称点P 、P"连接PP 、P E,PE,P"F,PF,PP"
由对称性可知PE+EF+FP=P E+EF+FP"=P P",且P 、E、F、P"在一条直线上,所以P P"即为最短距离,其长度取决于PA的长度,
如图(4),作出弧BC的圆心O,连接AO,与弧BC交于P,P点即为使得PA最短的点,∵AB=6km,AC=3km,∠BAC=60°,
∴ ABC是直角三角形,∠ABC=30°,BC=3,
BC所对的圆心角为60°,∴ OBC是等边三角形,∠CBO=60°,BO=BC=3,
∴∠ABO=90°,AO=3,PA=3-3,
∠P AE=∠EAP,∠PAF=∠FAP",
∴∠P AP"=2∠ABC=120°,P A=AP",
∴∠AP E=∠AP"F=30°,
∵P P"=2P Acos∠AP E=P A=3-9,
所以PE+EF+FP的最小值为3-9km.
【点睛】本题考查了圆的综合题,涉及到垂径定理、最短路径问题等,正确添加辅助线、灵活应用相关知识是解题的关键.
23.(1)证明见解析;(2)增大.
【分析】(1)根据锐角三角函数的定义进行比较即可;
(2)由(1)可总结出规律.
【详解】解:(1)∵,
∴ 和均为直角三角形,
∴ ,,
∴ ;
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
【点睛】本题考查锐角三角函数的增减性.
24.(1)见解析
(2)
【分析】(1)如图1,连接,由,,可得,,则,由,可得,进而结论得证;
(2)如图1,过点B作于点E,由,可得,则,由题意知,,则,可求,由勾股定理得,,设,则,由勾股定理得,,即,可求,证明,则,即,计算求解即可.
【详解】(1)证明:如图1,连接.
∵,,
∴,,
∴,
∵,
∴,
∴,即,
∴,
又∵是半径,
∴是的切线.
(2)解:如图1,过点B作于点E,
∴,
∴,
∴,
由题意知,,
∴,
解得,
由勾股定理得,,
设,则,
由勾股定理得,,即,
解得.
∴.
∵,
∴,
又∵,
∴,
∴,即,
解得,
∴的半径长为.
【点睛】本题考查了切线的判定,等边对等角,正弦,勾股定理,相似三角形的判定与性质等知识.熟练掌握切线的判定,等边对等角,正弦,勾股定理,相似三角形的判定与性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
28.1锐角三角函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在菱形中,,E是上一点,连接,将沿AE翻折,使点B落在点F处,连接.若,则的值为( )
A. B. C. D.
2.关于x的一元二次方程x2﹣4sinα x+2=0有两个等根,则锐角α的度数是( )
A.30° B.45° C.60° D.90°
3.如图,一个人从山脚下的A点出发,沿山坡小路AB走到山顶B点.已知坡角为20°,山高千米.用科学计算器计算小路AB的长度,下列按键顺序正确的是( )
A. B. C. D.
4.如果∠A是锐角,且sinA=,那么cos(90°-∠A)等于( )
A. B. C. D.
5.在中,,,,那么的正切值是( )
A. B.7 C. D.
6.如图,在中,,,,则
A. B. C. D.
7.如图所示,在边长相同的小正方形组成的网格中,两条经过格点的线段相交所成的锐角为α,则夹角α的正弦值为( )
A. B. C. D.1
8.已知Rt△ABC中,∠C=90 ,AC=4,BC=6,那么下列各式中,正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
9.如图,在4×4的正方形网格中,每个小正方形的边长都为1,点A、B、C、D均在格点上,下列结论正确的是( )
A.∠CDB=60° B.△ABC≌△CBD C.AC=CD D.∠ABC=∠CBD
10.如图,在中,,于,若AC=12,AB=13,则的值为( )
A.5:12 B.13:12 C.12:5 D.5:13
11.图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,,则双翼边缘端点C与D之间的距离为( )
A. B.
C. D.
12.在△ABC中,若|sinA﹣|+(﹣cosB)2=0,∠A,∠B都是锐角,则∠C度数是( )
A.75° B.90° C.105° D.120°
二、填空题
13.如图所示的网格是正方形网格,则∠AOB ∠COD.(填“>”,“=”或“<”)
14.如图,已知为斜边上的高,且,,那么等于 cm.
15.计算: .
16.若,则锐角 锐角(填、或).
17.在中,,,,则的值是 .
三、解答题
18.计算:.
19.如图,线段放置在正方形网格中,现请你分别在图1、图2、图3画出格点,使得是直角三角形,且的值分别为1、2、3.(工具只能用直尺)
20.【问题提出】
(1)如图1,,A、D在上,B、C在上,,若,则的长为__________;
【问题探究】
(2)如图2,已知是等边三角形,D、E分别为上的点,且,连接.求证:;
【问题解决】
(3)如图3是某公园一块四边形空地,其中,米,米,,P、Q分别在上,且,是平行于的一条绿化带,E、F是线段上的两个动点(点E在点F的左侧),米,M在线段上运动(不含端点),且保持,管理人员计划沿铺设两条笔直的水管,为了节省费用,公园负责人要求这两条水管的长度之和(即的值)最小,求这两条水管的长度之和的最小值.(绿化带、水管宽度均忽略不计)
21.北京冬奥会的滑雪大跳台在2022年北京冬奥会后成为世界首例永久性保留和使用的滑雪大跳台场馆,成为专业体育比赛和训练场地.如图,大跳台的横截面ABCD为梯形、高为136米、赛道AB边的坡比为.由于下雪造成赛道积雪至跳台底部E处,从E处测得跳台顶部A处的仰角为58°.
(1)请求出的值;
(2)试求出BE的长.(参考数据:,,)
22.问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
23.已知:如图,,、是上的两点,.
(1)求证:;
(2)锐角的正切函数值随角度的增大而________.
24.如图,在中,是弦,过点O作与交于点C,在的延长线取点D,使.
(1)求证:是的切线;
(2)若,,求的半径长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A A A A B D D A
题号 11 12
答案 D C
1.D
【分析】设与的交点为,,根据折叠的性质,可得,根据,可得为等腰直角三角形,从而得到,利用直角三角形的性质即可求解.
【详解】解:设与的交点为,设,则
由菱形的性质可得,,
由折叠的性质可得,,
则,
∴为等腰直角三角形,,
∴,即,
在中,,,
∴,
,
,
故选:D
【点睛】此题考查了菱形的性质,折叠的性质,解直角三角形,解题的关键是熟练掌握相关基本性质,确定.
2.B
【分析】先利用判别式的意义得到△=16sin2α-4×2=0,然后求出α的正弦值,再利用特殊角的三角函数值确定锐角α的度数.
【详解】根据题意得△=16sin2α-4×2=0,
所以sinα=,
所以锐角α=45°.
故选B.
【点睛】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了特殊角的三角函数值.
3.A
【分析】在△ABC中,通过解直角三角形可得出sinA= ,则,即可得出结论.
【详解】解:在△ABC中,sinA=sin20°= ,
∴,
∴按键顺序为:2÷sin20=
故选:A.
【点睛】本题主要考查解直角三角形的应用-坡度坡角问题以及计算器,熟练应用计算器是解题关键.
4.A
【分析】根据互为余角三角函数关系,解答即可.
【详解】解:∵α为锐角,sinα=,
∴cos(90°-α)=sinα=,
故选A.
【点睛】本题主要考查了互为余角的三角函数值,解决本题的关键是要熟记三角函数关系式.
5.A
【分析】本题主要考查了求角的正切值,熟知在直角三角形一个角的正切值等于该角的对边比上另一条直角边是解题的关键.
【详解】解:∵在中,,,,
∴,
故选A.
6.A
【分析】先利用勾股定理求出斜边AB,再求出sinB即可.
【详解】∵在中,,,,
∴,
∴.
故答案为A.
【点睛】本题考查的知识点是锐角三角函数的定义,解题关键是熟记三角函数的定义.
7.B
【分析】如图,设AB与CD交于点E,过点C作CF∥AB,连接DF,可得,设小正方形的边长为1,然后根据勾股定理及逆定理可得△CDF为等腰直角三角形,从而得到∠C=45°,即可求解.
【详解】解:如图,设AB与CD交于点E,过点C作CF∥AB,连接DF,
∵CF∥AB,
∴,
设小正方形的边长为1,
根据勾股定理得:,
,
,
∴,DF=CF,
∴△CDF为等腰直角三角形,
∴∠C=45°,
∴,
∴夹角α的正弦值为.
故选:B
【点睛】本题主要考查了勾股定理及其逆定理,锐角三角函数,根据题意,做适当辅助线构造出直角三角形是解题的关键.
8.D
【分析】本题可以利用锐角三角函数的定义以及勾股定理分别求解,再进行判断即可.
【详解】∵∠C=90°,BC=6,AC=4,
∴AB=,
A、sinA=,故此选项错误;
B、cosA=,故此选项错误;
C、tanA=,故此选项错误;
D、tanB=,故此选项正确.
故选:D.
【点睛】此题主要考查了锐角三角函数的定义以及勾股定理,熟练应用锐角三角函数的定义是解决问题的关键.
9.D
【分析】根据勾股定理可以得到 BC 、 CD 、 BD 的长,再根据勾股定理的逆定理可以得到△BCD 的形状,根据图形,很容易判断△ABC≌△CBD和AC = CD 不成立;再根据锐角三角函数可以得到∠ABC 和∠CBD的关系.
【详解】由图可得,
BC =,
CD =,
BD =,
∴BC2 + CD2 ==BD2,
∴△BCD 是直角三角形,
∴,
∵,
∴∠CDB≠60°,故选项A错误,不符合题意;
由图可知,显然△ABC 和△CBD 不全等,故选项 B错误,不符合题意;
∵AC =2,CD =,
∴AC ≠ CD ,故选项 C 错误,不符合题意;
∵,
∴∠ABC =∠CBD ,故选项 D 正确.
【点睛】本题考查相似三角形的判与性质、勾股定理与勾股定理的逆定理、锐角三角函数,解答本题的关键是明确题意,利用数形结合的思想解答.
10.A
【分析】证明∠BCD=∠A,求tanA即可.根据三角函数的定义求解.
【详解】由勾股定理知,c2=a2+b2
∴BC=.
根据同角的余角相等,∠BCD=∠A.
∴tan∠BCD=tan∠A=.
故选A.
【点睛】本题利用了等角进行转换求解,考查三角函数的定义.
11.D
【分析】作辅助线如图,由题意可得,,解直角三角形求出,然后根据即可得出答案.
【详解】解:如图,作直线,交双翼闸机于点E、F,则,
由题意可得,,
在直角三角形中,∵,
∴,
∴;
故选:D.
【点睛】本题考查了解直角三角形的应用,正确理解题意、熟练掌握锐角三角函数的知识是解题的关键.
12.C
【详解】解:由题意得:|sinA﹣|=0,(﹣cosB)2=0,
∴sinA﹣=0,﹣cosB=0,
∴sinA=, =cosB,
∴∠A=45°,∠B=30°,
∴∠C=180°﹣∠A﹣∠B=105°.
故选C.
【点睛】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握二次根式、绝对值、非负数等考点的运算.
13.=
【分析】根据tan∠AOB与tan∠COD的大小比较即可求解.
【详解】解:根据题意可知tan∠AOB=2,tan∠COD=2,
∴∠AOB=∠COD,
故答案为=.
【点睛】本题考查了锐角三角函数的增减性,构建直角三角形求角的三角函数值进行判断,熟练掌握锐角三角函数的增减性是关键.
14.
【分析】由题意易得,则有,然后可得,进而根据计算求解即可.
【详解】解:∵AD⊥BC,
∴,
在中,由勾股定理得,
∴,
∵∠CAB=90°,
∴;
故答案为:.
【点睛】本题考查了解直角三角形余弦,勾股定理等知识.熟练掌握余弦的求解是解题的关键.
15.-2
【分析】先根据二次根式、负整数指数幂、特殊三角函数值、0指数幂进行化简,再计算即可.
【详解】原式=.
故答案为:-2.
【点睛】本题考查实数的混合运算,解题的关键是根据二次根式、负整数指数幂、特殊三角函数值、0指数幂进行化简.
16.
【分析】本题考查了正弦的定义,根据在锐角范围内,正弦的函数值随着角度的增大而增大即可得出答案,熟练掌握相关知识点是解此题的关键.
【详解】解:∵在锐角范围内,正弦的函数值随着角度的增大而增大,
∴若,则锐角锐角,
故答案为:.
17.
【分析】先由勾股定理求解,再由锐角的正弦的定义可得:,从而可得答案.
【详解】解:如图, ,,,
故答案为:
【点睛】本题考查的是锐角的正弦的定义,勾股定理的应用,掌握锐角的正弦的定义是解题的关键.
18.
【分析】本题考查了特殊角三角函数值的混合运算,注意计算的准确性即可.
【详解】解:原式
.
19.见解析
【分析】根据勾股定理以及正切值对应边关系即可得到结果
【详解】解:如图所示:,
如图所示:,
如图所示:,
【点睛】本题考查了应用与设计作图、锐角三角函数关系及勾股定理,正确构造直角三角形是解决问题的关键
20.(1)5(2)见解析(3)390米
【分析】(1)首先根据条件证明四边形是平行四边形,再根据平行四边形对边相等可得到即可;
(2)根据证明,进而解答即可;
(3)连接,过点D作于,根据米,求出米,米,证明,可得,在上截取米,连接,可得四边形是平行四边形,,则,根据,可得的最小值为的长,利用勾股定理即可求解.
【详解】解:(1)∵,A、D在上,B、C在上,
∴,
∵
∴四边形是平行四边形,
∴
故答案为:5;
(2)证明:∵为等边三角形,
∴,
在与中,
,
∴,
∴;
(3)解:连接,过点D作于H,
∵,
∴,
设,则,
∵米,,
∴,
解得(负值舍去),
∴米,米,
∵,
∴,
∴,
∵,
∴,
∴,
在上截取米,连接,
∵,
∴四边形是平行四边形,
∴,
∴,
∵,
∴的最小值为的长,
∵(米),
∴(米),
∴这两条水管的长度之和的最小值为390米.
【点睛】本题主要考查平行四边形的判定和性质,等边三角形的性质,全等三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题.
21.(1)
(2)3.4米
【分析】(1)根据坡比的概念即可求得的正切值;
(2)过点A作交CE于点F,根据题意得出,,然后分别利用和的正切求出、的值,最后根据线段的和差即可得出答案.
【详解】(1)赛道AB边的坡比为
(2)过点A作交CE于点F
则,
在中,
∴
在中,
∴
∴
答:BE长度约为3.4米.
【点睛】本题考查了解直角三角形的应用-仰角俯角问题,能够正确地构建出直角三角形,将实际问题化归为解直角三角形的问题是解答问题的关键.
22.(1)5;(2)18;(3)(3-9)km.
【详解】【分析】(1)如图(1),设外接圆的圆心为O,连接OA, OB,根据已知条件可得△AOB是等边三角形,由此即可得半径;
(2)如图(2)所示,连接MO并延长交⊙O于N,连接OP,显然,MN即为MP的最大值,根据垂径定理求得OM的长即可求得MN的最大值;
(3) 如图(3)所示,假设P点即为所求点,分别作出点P关于AB、AC的对称点P 、P"连接PP 、P E,PE,P"F,PF,PP",则P P"即为最短距离,其长度取决于PA的长度, 根据题意正确画出图形,得到点P的位置,根据等边三角形、勾股定理等进行求解即可得PE+EF+FP的最小值.
【详解】(1)如图(1),设外接圆的圆心为O,连接OA, OB,
∵O是等腰三角形ABC的外心,AB=AC,
∴∠BAO=∠OAC=∠BAC==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OB=AB=5,
故答案为5;
(2)如图(2)所示,连接MO并延长交⊙O于N,连接OP,
显然,MP≤OM+OP=OM+ON=MN,ON=13,OM==5,MN=18,
∴PM的最大值为18;
(3) 如图(3)所示,假设P点即为所求点,分别作出点P关于AB、AC的对称点P 、P"连接PP 、P E,PE,P"F,PF,PP"
由对称性可知PE+EF+FP=P E+EF+FP"=P P",且P 、E、F、P"在一条直线上,所以P P"即为最短距离,其长度取决于PA的长度,
如图(4),作出弧BC的圆心O,连接AO,与弧BC交于P,P点即为使得PA最短的点,∵AB=6km,AC=3km,∠BAC=60°,
∴ ABC是直角三角形,∠ABC=30°,BC=3,
BC所对的圆心角为60°,∴ OBC是等边三角形,∠CBO=60°,BO=BC=3,
∴∠ABO=90°,AO=3,PA=3-3,
∠P AE=∠EAP,∠PAF=∠FAP",
∴∠P AP"=2∠ABC=120°,P A=AP",
∴∠AP E=∠AP"F=30°,
∵P P"=2P Acos∠AP E=P A=3-9,
所以PE+EF+FP的最小值为3-9km.
【点睛】本题考查了圆的综合题,涉及到垂径定理、最短路径问题等,正确添加辅助线、灵活应用相关知识是解题的关键.
23.(1)证明见解析;(2)增大.
【分析】(1)根据锐角三角函数的定义进行比较即可;
(2)由(1)可总结出规律.
【详解】解:(1)∵,
∴ 和均为直角三角形,
∴ ,,
∴ ;
(2)由(1)可知锐角的正切函数值随角度的增大而增大.
【点睛】本题考查锐角三角函数的增减性.
24.(1)见解析
(2)
【分析】(1)如图1,连接,由,,可得,,则,由,可得,进而结论得证;
(2)如图1,过点B作于点E,由,可得,则,由题意知,,则,可求,由勾股定理得,,设,则,由勾股定理得,,即,可求,证明,则,即,计算求解即可.
【详解】(1)证明:如图1,连接.
∵,,
∴,,
∴,
∵,
∴,
∴,即,
∴,
又∵是半径,
∴是的切线.
(2)解:如图1,过点B作于点E,
∴,
∴,
∴,
由题意知,,
∴,
解得,
由勾股定理得,,
设,则,
由勾股定理得,,即,
解得.
∴.
∵,
∴,
又∵,
∴,
∴,即,
解得,
∴的半径长为.
【点睛】本题考查了切线的判定,等边对等角,正弦,勾股定理,相似三角形的判定与性质等知识.熟练掌握切线的判定,等边对等角,正弦,勾股定理,相似三角形的判定与性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
