第十七章勾股定理同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
第十七章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
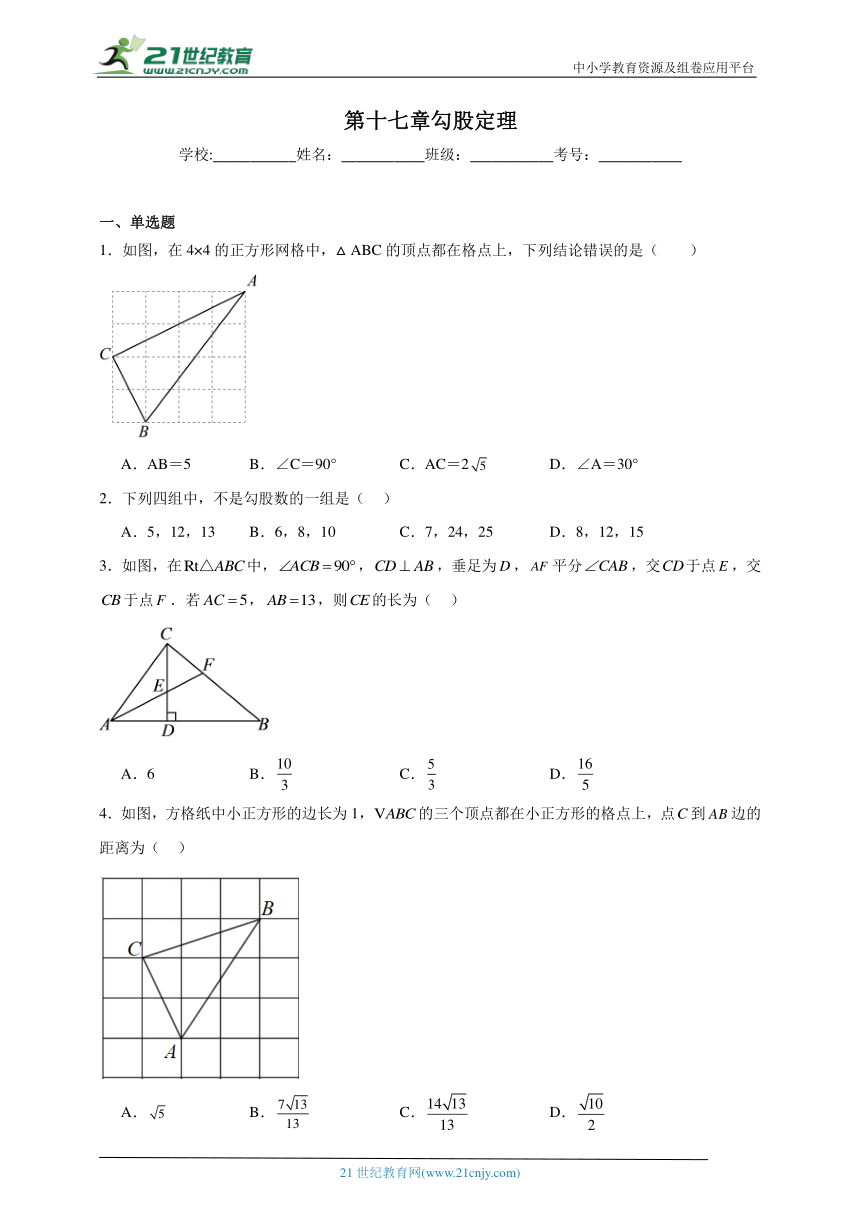
1.如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是( )
A.AB=5 B.∠C=90° C.AC=2 D.∠A=30°
2.下列四组中,不是勾股数的一组是( )
A.5,12,13 B.6,8,10 C.7,24,25 D.8,12,15
3.如图,在中,,,垂足为,平分,交于点,交于点.若,,则的长为( )
A.6 B. C. D.
4.如图,方格纸中小正方形的边长为1,的三个顶点都在小正方形的格点上,点到边的距离为( )
A. B. C. D.
5.如图,在四边形中,,,平分,点是的中点,点是上的动点,若,则的最小值为( )
A.2 B.4 C.6 D.8
6.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.
A.1 B.2 C.3 D.4
7.下列各组中的三个数值,能够构成直角三角形的是( )
A.2,3,4 B.60,61,10 C.,, D.3,4,5
8.满足的三个正整数a、b、c,被称为勾股数.下列各组数是勾股数的是( )
A.7,24,25 B.,, C.1.5,2,2.5 D.,,
9.下列各组数中不能作为直角三角形的三边长的是( ).
A.6、8、10 B.1、1、
C.2、6、 D.7、24、25
10.如图,龙城初级中学操场上有两棵树和(都与水平地面垂直),大树高14米,树梢D到树的水平距离()的长度为9米,小树高2米,一只小鸟从树梢D飞到树梢B,则它至少要飞行的长度为( )
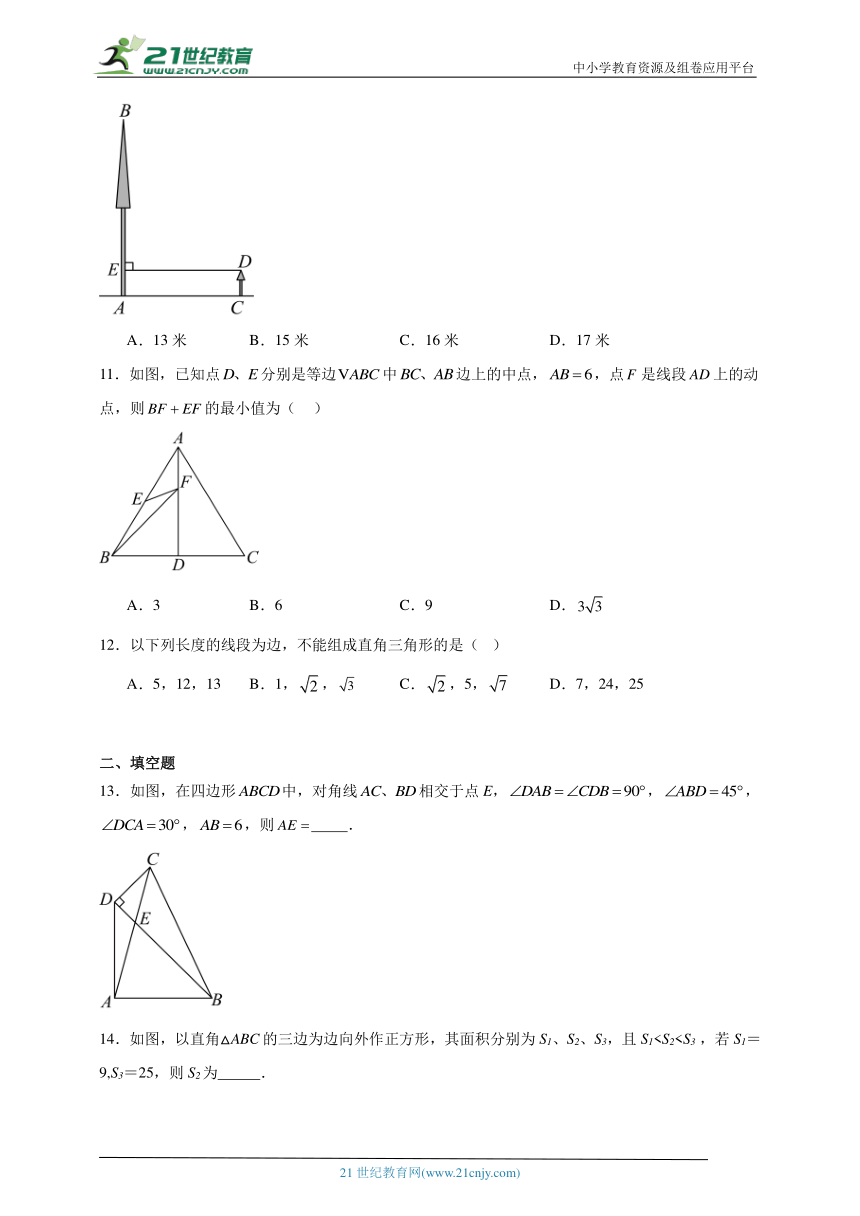
A.13米 B.15米 C.16米 D.17米
11.如图,已知点分别是等边中边上的中点,,点是线段上的动点,则的最小值为( )
A.3 B.6 C.9 D.
12.以下列长度的线段为边,不能组成直角三角形的是( )
A.5,12,13 B.1,, C.,5, D.7,24,25
二、填空题
13.如图,在四边形中,对角线相交于点E,,,,,则 .
14.如图,以直角△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S115.如图,有一张直角三角形纸片,两直角边,,将折叠,使点E与点A重合,折痕为DC,则 .
16.如图,在中,,,,,点是斜边上的一个动点,连接,将沿折叠得到,若的形状为直角三角形,那么的长是 .
17.△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为 ,
此三角形为 .
三、解答题
18.阅读材料:我们来看看完全平方公式在无理数化简中的作用.
问题提出:该如何化简
建立模型:形如的化简,只要我们找到两个数a,b,使,,这样,.
那么便有:,
问题解决:化简:,
解:首先把化为,这里,,由于,,即,.
.
模型应用1:利用上述解决问题的方法进行化简:
(1);
(2)小张同学在化简时,解决这个问题的过程如下.
①
②
③
④
在上述化简过程中,第_______步出现了错误,化简的正确结果为_______.
模型应用2:
(3)在中,,,,那么边的长为_______(结果化成最简).
19.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在直线l上画出点P,使PB+PC的值最小,且这个最小值为______________.
20.为进一步改善校园环境和面貌,消除校园安全隐患,提升校园环境品质,完善基础设施建设,某学校利用暑假全力做好教学条件提升改造工程.如图,某教室外部墙面上有破损处(看作点A),现维修师傅需借助梯子完成维修工作.梯子的长度为,将其斜靠在这面墙上,测得梯子底部E离墙角N处,维修师傅爬到梯子顶部使用仪器测量,此时的梯于顶部D与A相距.
(1)求教室外墙面破损处A距离地面的高度;
(2)为了方便施工,需要将梯子底部向内移动至离墙角处,求此时梯子顶部距离墙面破损处A的高度.
21.勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一,如图,有一架秋千,当它静止在的位置时,踏板离地的垂直高度为,将秋千往前推送,到达的位置,此时,秋千的踏板离地的垂直高度为,秋千的绳索始终保持拉直的状态.
(1)求秋千的长度;
(2)如果将秋千往前推送4米,求此时踏板离地的垂直高度为多少?
22.在学习了勾股定理之后,甲乙丙三位同学在方格图(正方形的边长都为1)中比赛找“整数三角形”,什么叫“整数三角形”呢?他们三人规定:边长和面积都是整数的三角形才能叫“整数三角形”.甲同学很快找到了如图1的“整数三角形”,一会儿后乙同学也找到了周长为24的“整数三角形”.丙同学受到甲、乙两同学的启发找到了两个不同的等腰“整数三角形”.请完成:
(1)以点A为一个顶点,在图2中作出乙同学找到的周长为24的“整数三角形”,并在每边周边标注其边长;
(2)在图3中作出两个不同的等腰“整数三角形”,并在每边周边标注其边长;
(3)你还能找到一个等边“整数三角形”吗?若能找出,请写出它的边长;若不能,请说明理由.
23.如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.
(1)求证:△ABD是等边三角形;
(2)若E为线段CD的中点,且AD=4,点P为线段AC上一动点,连接EP,BP.
①求EP+AP的最小值;
②求2BP+AP的最小值.
24.【模型呈现】
如图1,为的中线,交的延长线于点,求证:.
【应用1】
如图2,是的中线,交于点,交于点,且.若,,求线段的长.
【应用2】
如图3,在中,,为中点,,交于点E,交于点,连接.试猜想线段、、三者之间的数量关系,并说明理由.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B C D D A C B
题号 11 12
答案 D C
1.D
【分析】首先根据每个小正方形的边长为1,结合勾股定理求出AB、AC、BC的长,进而判断A、C的正误;再判断较短的两边的平方和与较长边的平方是否相等,进而可判断B的正误;在上步提示的基础上,判断BC与AB是否存在二倍关系,进而即可判断D的正误.
【详解】∵每个小正方形的边长为1,
根据勾股定理可得:AB=5,AC=2,BC=.
故A、C正确;
∵2+(2)2=52,
∴△ABC是直角三角形,
∴∠C=90°.
故B正确;
∵∠C=90°,AC=2BC,而非AB=2BC,
∴∠A≠30°.
故D错误.
故选D.
【点睛】本题考查的是三角形,熟练掌握三角形是解题的关键.
2.D
【分析】欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
【详解】A、,是勾股数,此选项错误;
B、=,是勾股数,此选项错误;
C、,是勾股数,此选项错误;
D、,不是勾股数,此选项正确;
故选D.
【点睛】此题主要考查了勾股数,解答此题掌握勾股数的定义是关键.
3.B
【分析】过点F作于点G.根据三角形内角和定理得出,,根据角平分线和对顶角相等得出,即可得出.由角平分线的性质定理可得出,又可证明,从而可求出.由勾股定理可求出.设,则,.在中,利用勾股定理可列出关于x的方程,解出x,即得出的长.
【详解】如图,过点F作于点G.
∵,
∴,
∴.
∵平分,
∴,
∴,
∴.
∵平分,,
∴.
又∵
∴,
∴,
∴.
∵,,,
∴.
设,则,.
∵在中,,
∴,
解得:,
∴.
故选B.
【点睛】本题考查角平分线的定义及其性质定理,等腰三角形的判定与性质,三角形全等的判定和性质,勾股定理等知识.正确作出辅助线并利用数形结合的思想是解题的关键.
4.B
【分析】利用分割图形求面积法求出△ABC的面积,利用勾股定理求出线段AB的长,再利用三角形的面积公式可求出点C到AB边的距离.
【详解】解:设点C到AB边的距离为h,则
∵,
又∵,
∴,
解得:;
故选:B.
【点睛】本题考查了勾股定理以及三角形的面积,利用面积法求出点C到AB边的距离是解题的关键.
5.C
【分析】连接,,,首先证明出,得到,然后证明出,得到,然后根据得到当点E,F,C三点共线时,的值最小,即的长度,然后利用勾股定理求出,证明出是等边三角形,得到,然后利用勾股定理求解即可.
【详解】如图所示,连接,,,
∵平分,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴当点E,F,C三点共线时,的值最小,即的长度,
∵平分,
∴
∵
∴
∴
∵,
∴是等边三角形
∵点是的中点,
∴
∴
∴
∴.
∴的最小值为6.
故选:C.
【点睛】此题考查了全等三角形的性质和判定,等边三角形的性质和判定,勾股定理,含角直角三角形的性质,解题的关键是熟练掌握以上知识点.
6.D
【详解】解:在直角△ABC中, ∵AB2=AC2+BC2.
∴AB=米.
则少走的距离是AC+BC AB=3+4-5=2米=4步,
故选:D.
7.D
【分析】根据勾股定理的逆定理逐项判断即可求解.
【详解】解:A.∵,∴ 不能构成直角三角形,不合题意;
B.∵,∴ 不能构成直角三角形,不合题意;
C.∵,∴ 不能构成直角三角形,不合题意;
D.∵,∴ 能构成直角三角形,符合题意.
故选:D
【点睛】本题考查了勾股定理逆定理的应用,理解勾股定理的逆定理是解题关键.
8.A
【分析】此题考查了勾股数,根据勾股数的定义逐项分析即可.
【详解】A.7,24,25是满足的三个正整数,故本选项符合题意;
B.,,是不满足的三个正整数,故本选项不符合题意;
C.1.5,2,2.5不全是正整数,故本选项不符合题意;
D.,,不全是正整数,故本选项不符合题意;
故选:A.
9.C
【分析】分别把选项中的三边平方后,根据勾股定理逆定理即可判断能否构成直角三角形.
【详解】A、∵62+82=102,∴能构成直角三角形,故此选项错误.
B、∵12+12=()2,∴能构成直角三角形,故此选项错误;
C、∵()2+22≠62,∴不能构成直角三角形,故此选项正确;
D、∵72+242=252,∴能构成直角三角形,故此选项错误.
故选C.
【点睛】此题考查勾股定理逆定理.解题关键在于在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
10.B
【分析】本题考查了勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.连接,求出米,然后由勾股定理求出的长即可.
【详解】解:如图,连接,
∵
∴
∵树高14米,米,
∴米,
∵米,
∴米,
故选:B.
11.D
【分析】本题考查轴对称求最短距离.连接交于点,连接,此时的值最小,最小值为.
【详解】解:连接交于点,连接,
是等边三角形,
,,
,
此时的值最小,最小值为,
,
的最小值为,
故选:D.
12.C
【分析】本题考查勾股定理的逆定理.掌握如果三角形两条短边的平方和等于第三边的平方,那么这个三角形就是直角三角形是解题关键.根据勾股定理逆定理逐项判断即可.
【详解】解:A.∵,∴5,12,13能组成直角三角形,,不符合题意;
B.∵,∴1,,能组成直角三角形,不符合题意;
C.∵,,5,不能组成直角三角形,符合题意;
D.∵,7,24,25能组成直角三角形,不符合题意.
故选:C.
13.
【分析】此题考查了勾股定理;含30度角的直角三角形;等腰直角三角形的性质等知识点,熟练掌握以上知识点是解决此类问题的关键.通过过点A作于点F,作含30度角的直角三角形,计算求解即可.
【详解】解:过点A作于点F,
∵,
∴,
在中,,
∵,
,
,
,
,
∴,
在中,,
,
,
,
,
,
∴.
故答案为.
14.16
【分析】先设Rt△ABC的三边分别为a、b、c,再分别用a、b、c表示S1、S2、S3的值,由勾股定理即可得出,继而可求得S2的值.
【详解】设Rt△ABC的三边分别为a、b、c,
∴,,,
∵△ABC 是直角三角形,
∴ ,即,
∴,
故答案为:16.
【点睛】此题主要考查了勾股定理,熟练掌握勾股定理以及正方形的面积公式是解本题的关键.
15.3
【分析】设,由翻折易得,,在中,根据勾股定理即可求得的长.
【详解】解:设,
∵两直角边,,
∴,
由折叠的性质得,
∴,,,
在中,,,,
,即,
∴,即,
故答案为:3.
【点睛】本题考查了翻折变换(折叠问题),勾股定理,熟记翻折前后对应边相等是解题的关键.
16.或
【分析】
本题考查折叠问题,含30度角的直角三角形,根据折叠得到当为直角三角形时,为直角三角形,分和,两种情况进行讨论求解即可.
【详解】解:∵将沿折叠得到,
∴当为直角三角形时,为直角三角形,
①当时:
∵,,
∴,
∴,
∴;
②当时,
∵,,
∴,
∴;
综上:的长是或;
故答案为:或.
17. 13 直角
【分析】根据三角形的三边关系知,求得第三边c应满足12-5=7<c<5+12=17,又因为这个数与a+b的和又是3的倍数,则可求得此数;然后利用直角三角形的判定方法判定三角形即可完成.
【详解】∵12-5=7<c<5+12=17,c又为奇数,
∴满足从7到17的奇数有9,11,13,15.
∵与a+b的和又是3的倍数,
∴a+b+c=30,
∴c=13.
∵52+122=132,
∴△ABC是直角三角形.
【点睛】本题是三角形的三边关系、勾股定理类型的题目,解答本题的关键是利用三角形的三边关系进行解答.
18.(1);(2),,;;(3)
【分析】(1)理解题干中问题解决的解题步骤,结合完全平方公式,以及二次根式的混合运算,即可解题;
(2)与(1)解题思想类似,写出该题解题步骤,再根据步骤判断其解题过程错误的地方,以及给出正确答案,即可解题;
(3)先利用勾股定理表示出,再利用平方差公式将其化为,最后用类似于前面2问的解题思路求解,即可解题.
【详解】解:(1),
,,
即,,
;
(2)①
②
③
④
在上述化简过程中,第1步不应该为除而是加,第步完全平方公式运用错误,第步二次根式化简错误,最后化简的正确结果为.
故答案为:,,;.
(3),,,
根据勾股定理可得:
.
故答案为:.
【点睛】本题考查了完全平方公式,二次根式的混合运算,平方差公式,勾股定理,解题的关键在于理解题干中的化简步骤.
19.(1)作图见解析;(2)这个最小值为.
【分析】(1)利用轴对称的性质分别作出,, 的对应点,,,然后连接起来即可.
(2)连接交于点,根据两点之间线段最短,点即为所求,利用勾股定理和结合图形,即可得到.
【详解】解:(1)如图,即为所求,其中A与A1重合.
如图示,连接交于点,点即为所求,
理由如下:∵B与B1是对应点,
∴,
∴,两点之间线段最短,点即为所求
∴.
【点睛】本题考查作图轴对称变换,两点之间线段最短等知识,掌握轴对称的性质,正确作出图形,是解题的关键.
20.(1)4.6m;
(2)0.6m.
【分析】本题考查勾股定理的应用;
(1)根据勾股定理求得,进而根据,即可求解;
(2)设是梯子移动后的位置,利用勾股定理求出,则.
【详解】(1)解:由题意,得,,,,
所以,
所以.
答:该教室外墙面破损处A距离地面有高.
(2)解:如图,此时是梯子移动后的位置.
∵在中,,.
∴由勾股定理,得.
梯子顶部与墙面破损处的距离为.
答:梯子顶部与墙面破损处的距离为.
21.(1)
(2)
【分析】本题考查勾股定理求线段长,涉及矩形的判定与性质等知识,数形结合,熟练运用勾股定理是解决问题的关键.
(1)由题中条件,得到四边形是矩形,从而得到,设秋千的长度为,则,,由勾股定理列方程求解即可得到答案;
(2)设时,,构造直角三角形,由勾股定理列方程求解即可得到答案.
【详解】(1)解:由题意知,
∵,,,
∴四边形是矩形,
∴
∴
∵,
∴,
设秋千的长度为,则,,
在中,由勾股定理得,即,
解得,
即秋千的长度是;
(2)解:设时,,
∵,
∴,
由(1)可知,,,
∴,
在中,,
由勾股定理得,则 ,
解得,
即此时踏板离地的垂直高度为.
22.(1)见解析;(2)见解析;(3)不能,理由见解析;
【分析】(1)根据勾股定理以及题目给的数据作出边长分别为的“整数三角形”;
(2)根据勾股定理,作出两个不同的等腰“整数三角形”可以是边长为的等腰三角形;
(3)根据题意先求得等边三角形的面积,比较面积和边长的关系即可得出不能找到等边“整数三角形”.
【详解】(1)如图1,以为顶点,周长为的直角“整数三角形”的边长为
以为顶点,周长为的直角“整数三角形”的边长为
如图:
(2)如图,根据勾股定理,作出两个不同的等腰“整数三角形”可以是边长为的等腰三角形
(3)不存在,理由如下:
如图,是等边三角形,是三角形边上的高,设(为正整数)
则
是整数,则是无理数,
不存在边长和面积都是整数的等边三角形
故找不到等边“整数三角形”.
【点睛】本题考查了勾股定理的应用,等边三角形的性质,熟练利用勾股定理找到勾股数是解题的关键.
23.(1)见解析;(2)①,②4
【分析】(1)根据线段的垂直平分线的性质定理,可得AD=AB,只要证明∠B=60°即可解决问题.
(2)①如图1中,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′.由∠PAF=30°,∠PFA=90°,推出PF=PA,推出PE+PA=PE+PF,所以当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,求出EF′即可解决问题.
②如图2中,作PF⊥AD于F,BF′⊥AD于F′,交AC于P′.由∠PAF=30°,∠PFA=90°,推出PF=PA,推出2BP+AP=2(PB+PA)=2(PB+PF),所以当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,求出BF′即可解决问题.
【详解】(1)证明:∵∠ACB=90°,∠BAC=30°
∴AC⊥BD,∠B=60°
∵DC=CB,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形.
(2)①如图1中,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′.
∵∠PAF=30°,∠PFA=90°,
∴PF=PA,
∴PE+PA=PE+PF,
∴当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,
在Rt△EF′B中,∵∠B=60°,EB=3,
∴ ,
同理易得: ,
∴
∴EP+AP的最小值为.
②如图2中,作PF⊥AD于F,BF′⊥AD于F′,交AC于P′.
∵∠PAF=30°,∠PFA=90°,
∴PF=PA,
∴2BP+AP=2(PB+PA)=2(PB+PF),
∴当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,
在Rt△DF′B中,∵∠D=60°,DB=4,
∴,
∴ ,
∴2BP+AP的最小值为4.
【点睛】本题考查三角形综合题、等边三角形的判定和性质、直角三角形30度角性质、最短问题等知识,解题的关键是学会添加常用辅助线,利用垂线段最短解决最短问题.
24.[模型呈现]证明见解析
[应用1] 7
[应用2],理由见解析
【分析】[模型呈现]证明即可得出结论;
[应用1]过点B作交延长线于点,由前面结论得到,结合条件,易证,,从而得解;
[应用2]过点作交延长线于点,连接,易证,得到,推出,再利用勾股定理即可得出结论.
【详解】[模型呈现]证明: ,
,.
为的中线,,
,
.
[应用1]解:过点B作交延长线于点,
,
是中线,
,
,
,
,
,
,
,,
.
.
[应用2]解:线段、、之间的等量关系为:.
理由如下:过点作交延长线于点,连接,
,,
是的中点,
,
,
,,
,
,
,
在中,由勾股定理得:,
.
【点睛】本题是三角形综合题,考查了全等三角形的判定和性质、等角对等边、垂直平分线的性质、勾股定理等知识,掌握全等三角形的判定和性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十七章勾股定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在4×4的正方形网格中,△ABC的顶点都在格点上,下列结论错误的是( )
A.AB=5 B.∠C=90° C.AC=2 D.∠A=30°
2.下列四组中,不是勾股数的一组是( )
A.5,12,13 B.6,8,10 C.7,24,25 D.8,12,15
3.如图,在中,,,垂足为,平分,交于点,交于点.若,,则的长为( )
A.6 B. C. D.
4.如图,方格纸中小正方形的边长为1,的三个顶点都在小正方形的格点上,点到边的距离为( )
A. B. C. D.
5.如图,在四边形中,,,平分,点是的中点,点是上的动点,若,则的最小值为( )
A.2 B.4 C.6 D.8
6.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.
A.1 B.2 C.3 D.4
7.下列各组中的三个数值,能够构成直角三角形的是( )
A.2,3,4 B.60,61,10 C.,, D.3,4,5
8.满足的三个正整数a、b、c,被称为勾股数.下列各组数是勾股数的是( )
A.7,24,25 B.,, C.1.5,2,2.5 D.,,
9.下列各组数中不能作为直角三角形的三边长的是( ).
A.6、8、10 B.1、1、
C.2、6、 D.7、24、25
10.如图,龙城初级中学操场上有两棵树和(都与水平地面垂直),大树高14米,树梢D到树的水平距离()的长度为9米,小树高2米,一只小鸟从树梢D飞到树梢B,则它至少要飞行的长度为( )
A.13米 B.15米 C.16米 D.17米
11.如图,已知点分别是等边中边上的中点,,点是线段上的动点,则的最小值为( )
A.3 B.6 C.9 D.
12.以下列长度的线段为边,不能组成直角三角形的是( )
A.5,12,13 B.1,, C.,5, D.7,24,25
二、填空题
13.如图,在四边形中,对角线相交于点E,,,,,则 .
14.如图,以直角△ABC的三边为边向外作正方形,其面积分别为S1、S2、S3,且S1
16.如图,在中,,,,,点是斜边上的一个动点,连接,将沿折叠得到,若的形状为直角三角形,那么的长是 .
17.△ABC的两边a,b分别为5,12,另一边c为奇数,且a+b+c是3的倍数,则c应为 ,
此三角形为 .
三、解答题
18.阅读材料:我们来看看完全平方公式在无理数化简中的作用.
问题提出:该如何化简
建立模型:形如的化简,只要我们找到两个数a,b,使,,这样,.
那么便有:,
问题解决:化简:,
解:首先把化为,这里,,由于,,即,.
.
模型应用1:利用上述解决问题的方法进行化简:
(1);
(2)小张同学在化简时,解决这个问题的过程如下.
①
②
③
④
在上述化简过程中,第_______步出现了错误,化简的正确结果为_______.
模型应用2:
(3)在中,,,,那么边的长为_______(结果化成最简).
19.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
(1)画出格点△ABC关于直线l对称的△A1B1C1;(要求:A与A1,B与B1,C与C1相对应)
(2)在直线l上画出点P,使PB+PC的值最小,且这个最小值为______________.
20.为进一步改善校园环境和面貌,消除校园安全隐患,提升校园环境品质,完善基础设施建设,某学校利用暑假全力做好教学条件提升改造工程.如图,某教室外部墙面上有破损处(看作点A),现维修师傅需借助梯子完成维修工作.梯子的长度为,将其斜靠在这面墙上,测得梯子底部E离墙角N处,维修师傅爬到梯子顶部使用仪器测量,此时的梯于顶部D与A相距.
(1)求教室外墙面破损处A距离地面的高度;
(2)为了方便施工,需要将梯子底部向内移动至离墙角处,求此时梯子顶部距离墙面破损处A的高度.
21.勾股定理是人类数学文化的一颗璀璨明珠,是用代数思想解决几何问题最重要的工具,也是数形结合的纽带之一,如图,有一架秋千,当它静止在的位置时,踏板离地的垂直高度为,将秋千往前推送,到达的位置,此时,秋千的踏板离地的垂直高度为,秋千的绳索始终保持拉直的状态.
(1)求秋千的长度;
(2)如果将秋千往前推送4米,求此时踏板离地的垂直高度为多少?
22.在学习了勾股定理之后,甲乙丙三位同学在方格图(正方形的边长都为1)中比赛找“整数三角形”,什么叫“整数三角形”呢?他们三人规定:边长和面积都是整数的三角形才能叫“整数三角形”.甲同学很快找到了如图1的“整数三角形”,一会儿后乙同学也找到了周长为24的“整数三角形”.丙同学受到甲、乙两同学的启发找到了两个不同的等腰“整数三角形”.请完成:
(1)以点A为一个顶点,在图2中作出乙同学找到的周长为24的“整数三角形”,并在每边周边标注其边长;
(2)在图3中作出两个不同的等腰“整数三角形”,并在每边周边标注其边长;
(3)你还能找到一个等边“整数三角形”吗?若能找出,请写出它的边长;若不能,请说明理由.
23.如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD.
(1)求证:△ABD是等边三角形;
(2)若E为线段CD的中点,且AD=4,点P为线段AC上一动点,连接EP,BP.
①求EP+AP的最小值;
②求2BP+AP的最小值.
24.【模型呈现】
如图1,为的中线,交的延长线于点,求证:.
【应用1】
如图2,是的中线,交于点,交于点,且.若,,求线段的长.
【应用2】
如图3,在中,,为中点,,交于点E,交于点,连接.试猜想线段、、三者之间的数量关系,并说明理由.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B B C D D A C B
题号 11 12
答案 D C
1.D
【分析】首先根据每个小正方形的边长为1,结合勾股定理求出AB、AC、BC的长,进而判断A、C的正误;再判断较短的两边的平方和与较长边的平方是否相等,进而可判断B的正误;在上步提示的基础上,判断BC与AB是否存在二倍关系,进而即可判断D的正误.
【详解】∵每个小正方形的边长为1,
根据勾股定理可得:AB=5,AC=2,BC=.
故A、C正确;
∵2+(2)2=52,
∴△ABC是直角三角形,
∴∠C=90°.
故B正确;
∵∠C=90°,AC=2BC,而非AB=2BC,
∴∠A≠30°.
故D错误.
故选D.
【点睛】本题考查的是三角形,熟练掌握三角形是解题的关键.
2.D
【分析】欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
【详解】A、,是勾股数,此选项错误;
B、=,是勾股数,此选项错误;
C、,是勾股数,此选项错误;
D、,不是勾股数,此选项正确;
故选D.
【点睛】此题主要考查了勾股数,解答此题掌握勾股数的定义是关键.
3.B
【分析】过点F作于点G.根据三角形内角和定理得出,,根据角平分线和对顶角相等得出,即可得出.由角平分线的性质定理可得出,又可证明,从而可求出.由勾股定理可求出.设,则,.在中,利用勾股定理可列出关于x的方程,解出x,即得出的长.
【详解】如图,过点F作于点G.
∵,
∴,
∴.
∵平分,
∴,
∴,
∴.
∵平分,,
∴.
又∵
∴,
∴,
∴.
∵,,,
∴.
设,则,.
∵在中,,
∴,
解得:,
∴.
故选B.
【点睛】本题考查角平分线的定义及其性质定理,等腰三角形的判定与性质,三角形全等的判定和性质,勾股定理等知识.正确作出辅助线并利用数形结合的思想是解题的关键.
4.B
【分析】利用分割图形求面积法求出△ABC的面积,利用勾股定理求出线段AB的长,再利用三角形的面积公式可求出点C到AB边的距离.
【详解】解:设点C到AB边的距离为h,则
∵,
又∵,
∴,
解得:;
故选:B.
【点睛】本题考查了勾股定理以及三角形的面积,利用面积法求出点C到AB边的距离是解题的关键.
5.C
【分析】连接,,,首先证明出,得到,然后证明出,得到,然后根据得到当点E,F,C三点共线时,的值最小,即的长度,然后利用勾股定理求出,证明出是等边三角形,得到,然后利用勾股定理求解即可.
【详解】如图所示,连接,,,
∵平分,
∴,
∵,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,
∴当点E,F,C三点共线时,的值最小,即的长度,
∵平分,
∴
∵
∴
∴
∵,
∴是等边三角形
∵点是的中点,
∴
∴
∴
∴.
∴的最小值为6.
故选:C.
【点睛】此题考查了全等三角形的性质和判定,等边三角形的性质和判定,勾股定理,含角直角三角形的性质,解题的关键是熟练掌握以上知识点.
6.D
【详解】解:在直角△ABC中, ∵AB2=AC2+BC2.
∴AB=米.
则少走的距离是AC+BC AB=3+4-5=2米=4步,
故选:D.
7.D
【分析】根据勾股定理的逆定理逐项判断即可求解.
【详解】解:A.∵,∴ 不能构成直角三角形,不合题意;
B.∵,∴ 不能构成直角三角形,不合题意;
C.∵,∴ 不能构成直角三角形,不合题意;
D.∵,∴ 能构成直角三角形,符合题意.
故选:D
【点睛】本题考查了勾股定理逆定理的应用,理解勾股定理的逆定理是解题关键.
8.A
【分析】此题考查了勾股数,根据勾股数的定义逐项分析即可.
【详解】A.7,24,25是满足的三个正整数,故本选项符合题意;
B.,,是不满足的三个正整数,故本选项不符合题意;
C.1.5,2,2.5不全是正整数,故本选项不符合题意;
D.,,不全是正整数,故本选项不符合题意;
故选:A.
9.C
【分析】分别把选项中的三边平方后,根据勾股定理逆定理即可判断能否构成直角三角形.
【详解】A、∵62+82=102,∴能构成直角三角形,故此选项错误.
B、∵12+12=()2,∴能构成直角三角形,故此选项错误;
C、∵()2+22≠62,∴不能构成直角三角形,故此选项正确;
D、∵72+242=252,∴能构成直角三角形,故此选项错误.
故选C.
【点睛】此题考查勾股定理逆定理.解题关键在于在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
10.B
【分析】本题考查了勾股定理的应用,正确作出辅助线构造直角三角形是解题的关键.连接,求出米,然后由勾股定理求出的长即可.
【详解】解:如图,连接,
∵
∴
∵树高14米,米,
∴米,
∵米,
∴米,
故选:B.
11.D
【分析】本题考查轴对称求最短距离.连接交于点,连接,此时的值最小,最小值为.
【详解】解:连接交于点,连接,
是等边三角形,
,,
,
此时的值最小,最小值为,
,
的最小值为,
故选:D.
12.C
【分析】本题考查勾股定理的逆定理.掌握如果三角形两条短边的平方和等于第三边的平方,那么这个三角形就是直角三角形是解题关键.根据勾股定理逆定理逐项判断即可.
【详解】解:A.∵,∴5,12,13能组成直角三角形,,不符合题意;
B.∵,∴1,,能组成直角三角形,不符合题意;
C.∵,,5,不能组成直角三角形,符合题意;
D.∵,7,24,25能组成直角三角形,不符合题意.
故选:C.
13.
【分析】此题考查了勾股定理;含30度角的直角三角形;等腰直角三角形的性质等知识点,熟练掌握以上知识点是解决此类问题的关键.通过过点A作于点F,作含30度角的直角三角形,计算求解即可.
【详解】解:过点A作于点F,
∵,
∴,
在中,,
∵,
,
,
,
,
∴,
在中,,
,
,
,
,
,
∴.
故答案为.
14.16
【分析】先设Rt△ABC的三边分别为a、b、c,再分别用a、b、c表示S1、S2、S3的值,由勾股定理即可得出,继而可求得S2的值.
【详解】设Rt△ABC的三边分别为a、b、c,
∴,,,
∵△ABC 是直角三角形,
∴ ,即,
∴,
故答案为:16.
【点睛】此题主要考查了勾股定理,熟练掌握勾股定理以及正方形的面积公式是解本题的关键.
15.3
【分析】设,由翻折易得,,在中,根据勾股定理即可求得的长.
【详解】解:设,
∵两直角边,,
∴,
由折叠的性质得,
∴,,,
在中,,,,
,即,
∴,即,
故答案为:3.
【点睛】本题考查了翻折变换(折叠问题),勾股定理,熟记翻折前后对应边相等是解题的关键.
16.或
【分析】
本题考查折叠问题,含30度角的直角三角形,根据折叠得到当为直角三角形时,为直角三角形,分和,两种情况进行讨论求解即可.
【详解】解:∵将沿折叠得到,
∴当为直角三角形时,为直角三角形,
①当时:
∵,,
∴,
∴,
∴;
②当时,
∵,,
∴,
∴;
综上:的长是或;
故答案为:或.
17. 13 直角
【分析】根据三角形的三边关系知,求得第三边c应满足12-5=7<c<5+12=17,又因为这个数与a+b的和又是3的倍数,则可求得此数;然后利用直角三角形的判定方法判定三角形即可完成.
【详解】∵12-5=7<c<5+12=17,c又为奇数,
∴满足从7到17的奇数有9,11,13,15.
∵与a+b的和又是3的倍数,
∴a+b+c=30,
∴c=13.
∵52+122=132,
∴△ABC是直角三角形.
【点睛】本题是三角形的三边关系、勾股定理类型的题目,解答本题的关键是利用三角形的三边关系进行解答.
18.(1);(2),,;;(3)
【分析】(1)理解题干中问题解决的解题步骤,结合完全平方公式,以及二次根式的混合运算,即可解题;
(2)与(1)解题思想类似,写出该题解题步骤,再根据步骤判断其解题过程错误的地方,以及给出正确答案,即可解题;
(3)先利用勾股定理表示出,再利用平方差公式将其化为,最后用类似于前面2问的解题思路求解,即可解题.
【详解】解:(1),
,,
即,,
;
(2)①
②
③
④
在上述化简过程中,第1步不应该为除而是加,第步完全平方公式运用错误,第步二次根式化简错误,最后化简的正确结果为.
故答案为:,,;.
(3),,,
根据勾股定理可得:
.
故答案为:.
【点睛】本题考查了完全平方公式,二次根式的混合运算,平方差公式,勾股定理,解题的关键在于理解题干中的化简步骤.
19.(1)作图见解析;(2)这个最小值为.
【分析】(1)利用轴对称的性质分别作出,, 的对应点,,,然后连接起来即可.
(2)连接交于点,根据两点之间线段最短,点即为所求,利用勾股定理和结合图形,即可得到.
【详解】解:(1)如图,即为所求,其中A与A1重合.
如图示,连接交于点,点即为所求,
理由如下:∵B与B1是对应点,
∴,
∴,两点之间线段最短,点即为所求
∴.
【点睛】本题考查作图轴对称变换,两点之间线段最短等知识,掌握轴对称的性质,正确作出图形,是解题的关键.
20.(1)4.6m;
(2)0.6m.
【分析】本题考查勾股定理的应用;
(1)根据勾股定理求得,进而根据,即可求解;
(2)设是梯子移动后的位置,利用勾股定理求出,则.
【详解】(1)解:由题意,得,,,,
所以,
所以.
答:该教室外墙面破损处A距离地面有高.
(2)解:如图,此时是梯子移动后的位置.
∵在中,,.
∴由勾股定理,得.
梯子顶部与墙面破损处的距离为.
答:梯子顶部与墙面破损处的距离为.
21.(1)
(2)
【分析】本题考查勾股定理求线段长,涉及矩形的判定与性质等知识,数形结合,熟练运用勾股定理是解决问题的关键.
(1)由题中条件,得到四边形是矩形,从而得到,设秋千的长度为,则,,由勾股定理列方程求解即可得到答案;
(2)设时,,构造直角三角形,由勾股定理列方程求解即可得到答案.
【详解】(1)解:由题意知,
∵,,,
∴四边形是矩形,
∴
∴
∵,
∴,
设秋千的长度为,则,,
在中,由勾股定理得,即,
解得,
即秋千的长度是;
(2)解:设时,,
∵,
∴,
由(1)可知,,,
∴,
在中,,
由勾股定理得,则 ,
解得,
即此时踏板离地的垂直高度为.
22.(1)见解析;(2)见解析;(3)不能,理由见解析;
【分析】(1)根据勾股定理以及题目给的数据作出边长分别为的“整数三角形”;
(2)根据勾股定理,作出两个不同的等腰“整数三角形”可以是边长为的等腰三角形;
(3)根据题意先求得等边三角形的面积,比较面积和边长的关系即可得出不能找到等边“整数三角形”.
【详解】(1)如图1,以为顶点,周长为的直角“整数三角形”的边长为
以为顶点,周长为的直角“整数三角形”的边长为
如图:
(2)如图,根据勾股定理,作出两个不同的等腰“整数三角形”可以是边长为的等腰三角形
(3)不存在,理由如下:
如图,是等边三角形,是三角形边上的高,设(为正整数)
则
是整数,则是无理数,
不存在边长和面积都是整数的等边三角形
故找不到等边“整数三角形”.
【点睛】本题考查了勾股定理的应用,等边三角形的性质,熟练利用勾股定理找到勾股数是解题的关键.
23.(1)见解析;(2)①,②4
【分析】(1)根据线段的垂直平分线的性质定理,可得AD=AB,只要证明∠B=60°即可解决问题.
(2)①如图1中,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′.由∠PAF=30°,∠PFA=90°,推出PF=PA,推出PE+PA=PE+PF,所以当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,求出EF′即可解决问题.
②如图2中,作PF⊥AD于F,BF′⊥AD于F′,交AC于P′.由∠PAF=30°,∠PFA=90°,推出PF=PA,推出2BP+AP=2(PB+PA)=2(PB+PF),所以当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,求出BF′即可解决问题.
【详解】(1)证明:∵∠ACB=90°,∠BAC=30°
∴AC⊥BD,∠B=60°
∵DC=CB,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形.
(2)①如图1中,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′.
∵∠PAF=30°,∠PFA=90°,
∴PF=PA,
∴PE+PA=PE+PF,
∴当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,
在Rt△EF′B中,∵∠B=60°,EB=3,
∴ ,
同理易得: ,
∴
∴EP+AP的最小值为.
②如图2中,作PF⊥AD于F,BF′⊥AD于F′,交AC于P′.
∵∠PAF=30°,∠PFA=90°,
∴PF=PA,
∴2BP+AP=2(PB+PA)=2(PB+PF),
∴当B、P、F共线时,即BF′⊥AD时,PB+PF最短,最小值为线段BF′,
在Rt△DF′B中,∵∠D=60°,DB=4,
∴,
∴ ,
∴2BP+AP的最小值为4.
【点睛】本题考查三角形综合题、等边三角形的判定和性质、直角三角形30度角性质、最短问题等知识,解题的关键是学会添加常用辅助线,利用垂线段最短解决最短问题.
24.[模型呈现]证明见解析
[应用1] 7
[应用2],理由见解析
【分析】[模型呈现]证明即可得出结论;
[应用1]过点B作交延长线于点,由前面结论得到,结合条件,易证,,从而得解;
[应用2]过点作交延长线于点,连接,易证,得到,推出,再利用勾股定理即可得出结论.
【详解】[模型呈现]证明: ,
,.
为的中线,,
,
.
[应用1]解:过点B作交延长线于点,
,
是中线,
,
,
,
,
,
,
,,
.
.
[应用2]解:线段、、之间的等量关系为:.
理由如下:过点作交延长线于点,连接,
,,
是的中点,
,
,
,,
,
,
,
在中,由勾股定理得:,
.
【点睛】本题是三角形综合题,考查了全等三角形的判定和性质、等角对等边、垂直平分线的性质、勾股定理等知识,掌握全等三角形的判定和性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
