5.1相交线课件(共41张PPT)
图片预览






文档简介
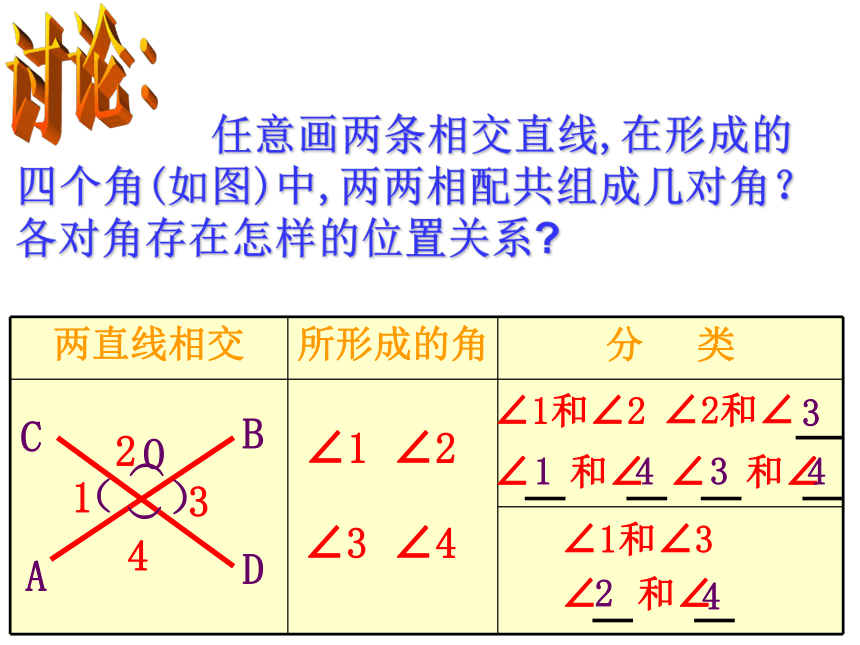
课件41张PPT。直线AB、CD相交于点O如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。握紧把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小直到剪开布片。如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题。 请你画出任意两条相交直线,用量角器量一量4个角的度数,看看这四个角有什么关系?问题:两条相交直线.形成的小于平角的
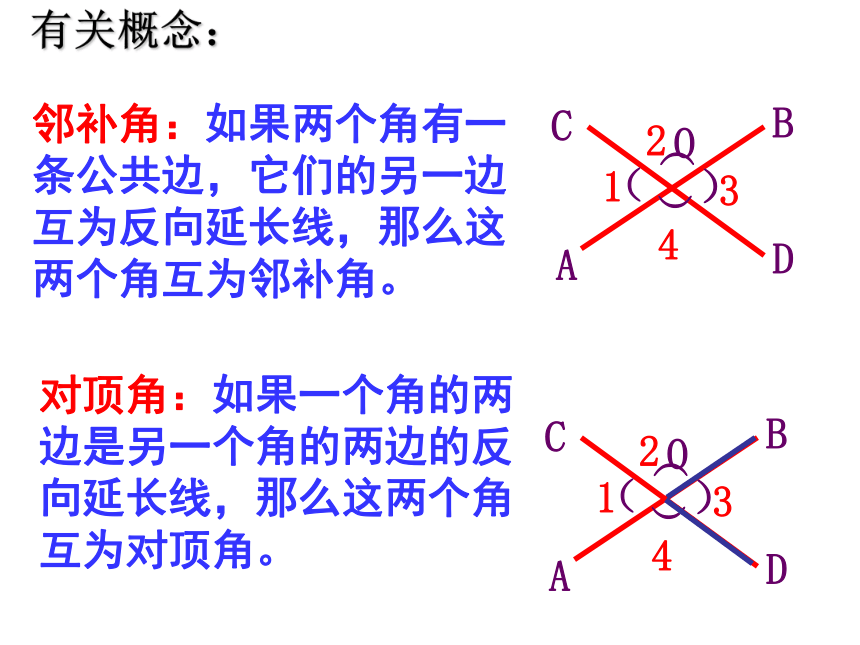
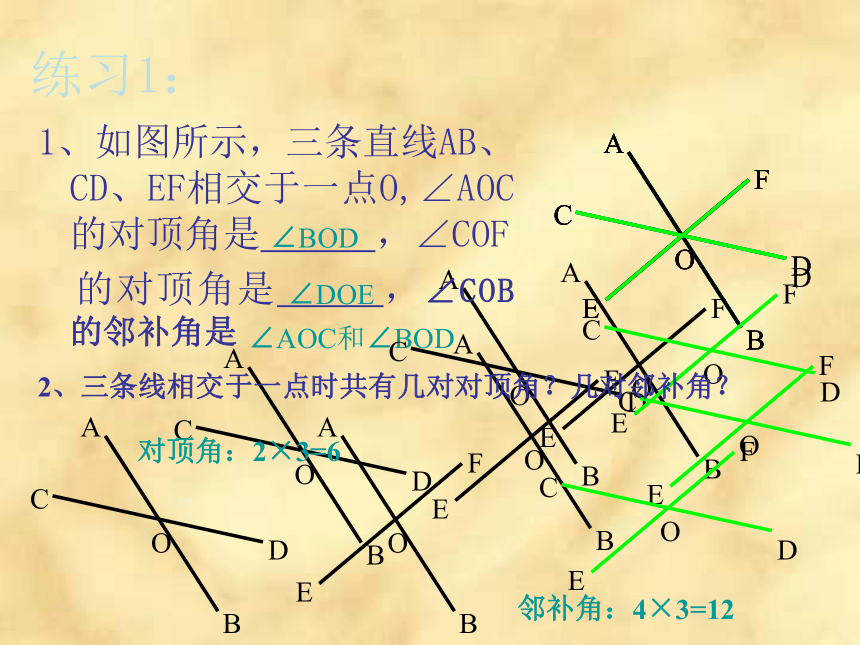
角有几个? 任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系?∠3∠1∠2∠4∠1和∠2414343∠1和∠32OABCD)(1342)(OABCD)(1342)( 有关概念:邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。对顶角:如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。练习1:∠BOD∠DOE∠AOC和∠BOD1、如图所示,三条直线AB、CD、EF相交于一点O,∠AOC的对顶角是 ,∠COF
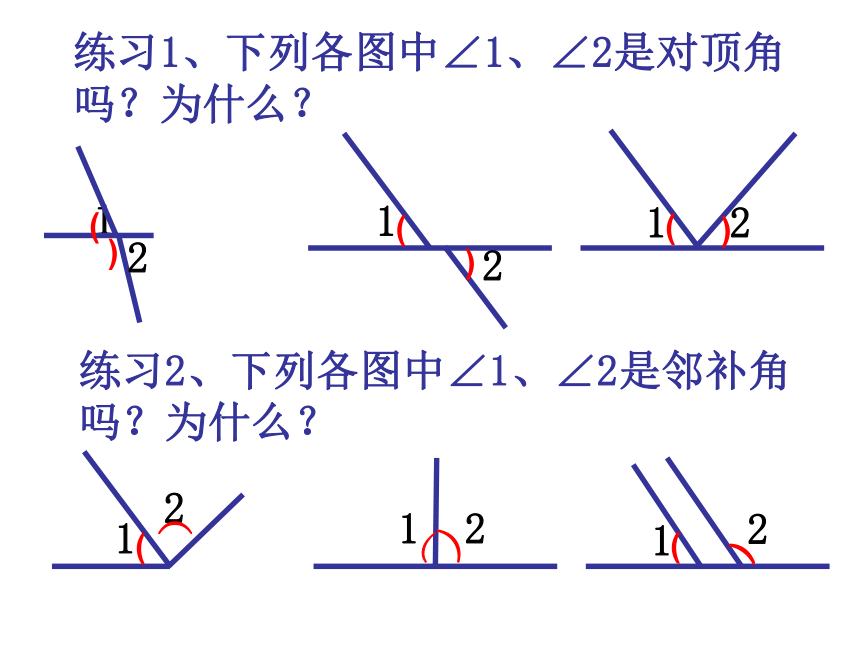
的对顶角是 ,∠COB的邻补角是 2、三条线相交于一点时共有几对对顶角?几对邻补角?对顶角:2×3=6邻补角:4×3=121练习1、下列各图中∠1、∠2是对顶角吗?为什么?21212)(()1练习2、下列各图中∠1、∠2是邻补角吗?为什么?21212)((()( 对顶角的性质:
对顶角相等.OABCD)(1342)( 为什么?已知:直线AB与CD相交于O
点(如图),
求证:∠1=∠3、 ∠2=∠4 证明:∵直线AB与CD相交于O点,∴∠1+∠2=180°、 ∠2+∠3=180°∴∠1=∠3同理可得:∠2=∠4∠2=180°-∠1
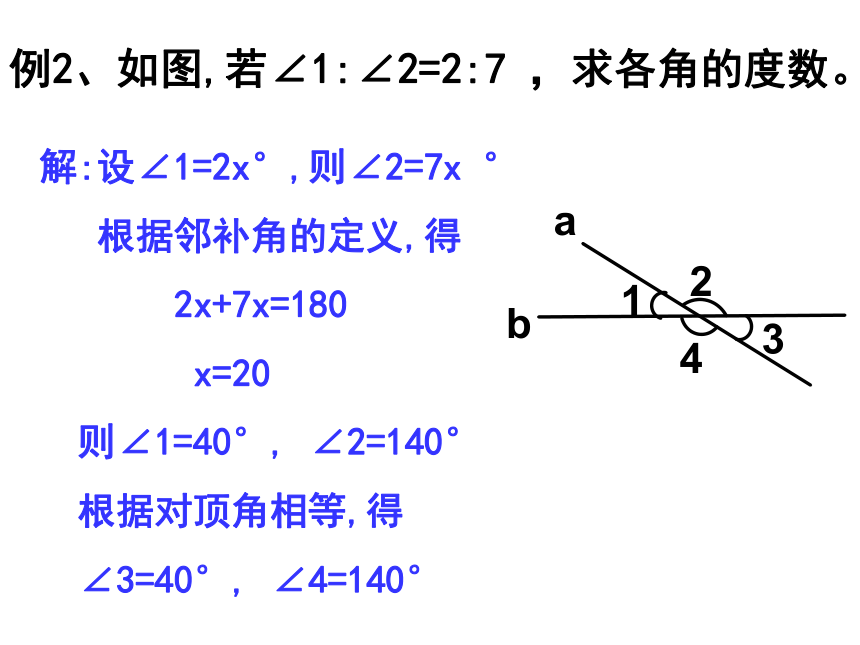
=180°- 40°解:由邻补角的定义,可得=140°由对顶角相等,可得若∠1+∠3=50° ,求各角的度数。若∠1= m°,求各角的度数。例题讲解例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠ 4的度数。例2、如图,若∠1:∠2=2:7 ,求各角的度数。解:设∠1=2x°,则∠2=7x °
根据邻补角的定义,得
2x+7x=180
x=20
则∠1=40°, ∠2=140°
根据对顶角相等,得
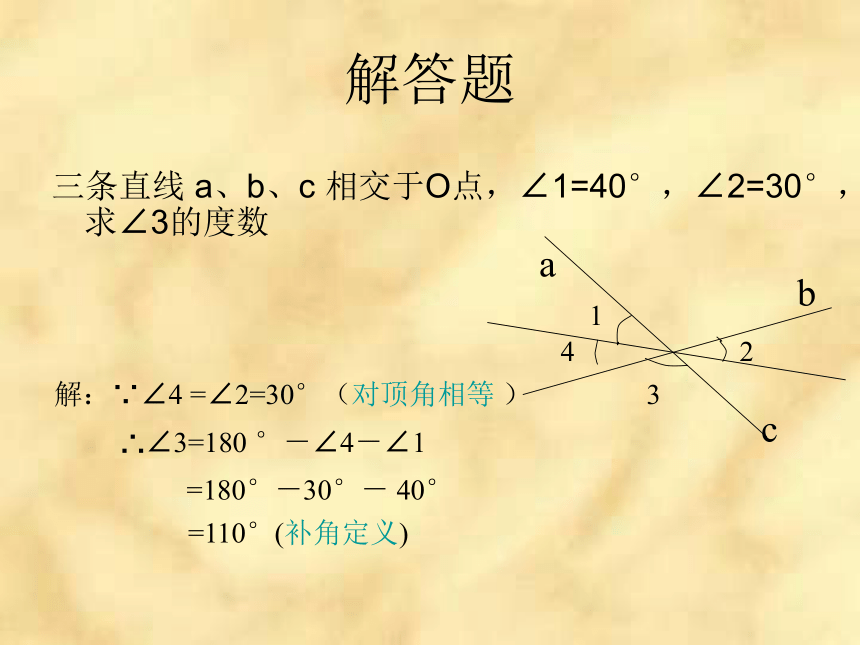
∠3=40°, ∠4=140°解答题三条直线 a、b、c 相交于O点,∠1=40°,∠2=30°,求∠3的度数解:∵∠4 =∠2=30°(对顶角相等 )∴∠3=180 °-∠4-∠1=180°-30°- 40°=110°(补角定义)看谁做得棒!已知:直线AB、CD相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD和∠BOC的度数。解:∵OA平分∠EOC
∠EOC=70°(已知)
∴∠AOC=35°(角平分线定义)
∴∠BOD=∠AOC=35°(对顶角相等)
∴∠BOC=180°-∠AOC
=108°-35°=145°(邻补角定义)达标测试一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A、∠AOC和∠BOE是对顶角;
B、∠COE和∠AOD是对顶角;
C、∠BOC和∠AOD是对顶角;
D、∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,
那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。ABCDOE×√√CC1、一个角的对顶角有 个,邻补角最多有 个,
而补角则可以有 个。一两无数三、填空题2、右图中∠AOC的对顶角是 ,
邻补角是 .∠DOB∠AOD和∠COB3、若∠1与∠2是对顶角,∠1=160,则∠2=______0;
若∠3与∠4是邻补角,则∠3+∠4 =______04、若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3= 05、如图1,∠2与∠3互为邻补角,∠1=∠2,则∠1与∠3的关系为 。图116180180互补归纳小结 对顶
角相
等
邻补
角互
补 ②有公共顶点;③没有公共边①两条直线相交形成的角; ①两条直线相交而成;②有公共顶点;③有一条公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,
对顶角只有两对
邻补角有四对 ①有无公共边5.1.2 垂线入水姿势特殊情况复习:BACDO1234在相交线的模型中,固定木条a,转动木条b,当α =90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.当α ≠90°时,a与b不垂直,叫斜交.两条直线相交斜交垂直垂直是相交的特殊情况)α abbbbb)α 观察与思考1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。一、垂直的定义日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?十字路口的两条道路围棋盘的横线和竖线铅垂线和水平线图1图4图3图2ba1)图形:Oα 2)文字:a、b互相垂直, 垂足为O3)符号:a⊥b或b⊥a,
若要强调垂足,
则记为:a⊥b, 垂足为O 2.垂直的表示:ABCDO书写形式:如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式:反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。②性质:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)(∠AOC=∠BOC=∠BOD=90°)3.垂直的书写形式:练习1.两条直线相交所成的四个角中,下列条件中能断定两条直线垂直的是( )
(A)有一个角为90° (B)有两个角相等
(C) 有三个角相等 (D)有四个角相等
(E)有四对邻补角 (F)有一对对顶角互补(G)有一对邻补角相等 (H)有两组角相等 A C D F G练一练如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35°, ∠2=55°,则OE与AB的位置关系
是 . 切记:要证垂直必先想到直角(90°)联想数学练习2:OE⊥ABACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55° 二、例题例1 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.(对顶角相等)1.在小学学段我们曾通过折纸的方法,得到两条垂线,现在你可以用几种折法得到两条垂线? 想一想 做一做2.如图(5):直线a上有一点A,经过点A,你能折出几条与a垂直的直线?如图(6):直线a外有一点B,经过点B,你能折出几条与a垂直的直线?想一想 做一做过点A、B分别可以做直线a的几条垂线呢?问题:
怎么样画垂线?垂线的画法问题:
这样画l的垂线可以画几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.请同学们画一下1.垂线的画法: 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.垂线的性质(1)①过点P 向线段AB 所在直线引垂线,正确的是( ). A B C D
C练一练练习3.EEE注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.②、练一练练习5、 点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,试确定OE与OF的位置关系.并说明理由.练一练1、垂线的定义2、垂线的画法3、垂线的性质(1)过一点有且只有一条直线与已知直线垂直一、放;二、靠;三、移;四、画 小结:
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
角有几个? 任意画两条相交直线,在形成的四个角(如图)中,两两相配共组成几对角?各对角存在怎样的位置关系?∠3∠1∠2∠4∠1和∠2414343∠1和∠32OABCD)(1342)(OABCD)(1342)( 有关概念:邻补角:如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角。对顶角:如果一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。练习1:∠BOD∠DOE∠AOC和∠BOD1、如图所示,三条直线AB、CD、EF相交于一点O,∠AOC的对顶角是 ,∠COF
的对顶角是 ,∠COB的邻补角是 2、三条线相交于一点时共有几对对顶角?几对邻补角?对顶角:2×3=6邻补角:4×3=121练习1、下列各图中∠1、∠2是对顶角吗?为什么?21212)(()1练习2、下列各图中∠1、∠2是邻补角吗?为什么?21212)((()( 对顶角的性质:
对顶角相等.OABCD)(1342)( 为什么?已知:直线AB与CD相交于O
点(如图),
求证:∠1=∠3、 ∠2=∠4 证明:∵直线AB与CD相交于O点,∴∠1+∠2=180°、 ∠2+∠3=180°∴∠1=∠3同理可得:∠2=∠4∠2=180°-∠1
=180°- 40°解:由邻补角的定义,可得=140°由对顶角相等,可得若∠1+∠3=50° ,求各角的度数。若∠1= m°,求各角的度数。例题讲解例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠ 4的度数。例2、如图,若∠1:∠2=2:7 ,求各角的度数。解:设∠1=2x°,则∠2=7x °
根据邻补角的定义,得
2x+7x=180
x=20
则∠1=40°, ∠2=140°
根据对顶角相等,得
∠3=40°, ∠4=140°解答题三条直线 a、b、c 相交于O点,∠1=40°,∠2=30°,求∠3的度数解:∵∠4 =∠2=30°(对顶角相等 )∴∠3=180 °-∠4-∠1=180°-30°- 40°=110°(补角定义)看谁做得棒!已知:直线AB、CD相交于O点,OA平分∠EOC,∠EOC=70°,求∠BOD和∠BOC的度数。解:∵OA平分∠EOC
∠EOC=70°(已知)
∴∠AOC=35°(角平分线定义)
∴∠BOD=∠AOC=35°(对顶角相等)
∴∠BOC=180°-∠AOC
=108°-35°=145°(邻补角定义)达标测试一、判断题
1、有公共顶点且相等的两个角是对顶角。( )
2、两条直线相交,有两组对顶角。 ( )
3、两条直线相交所构成的四个角中有一个角是直角,
那么其余的三个角也是直角。 ( )二、选择题
1、如右图直线AB、CD交于点O,OE为射线,那么( )
A、∠AOC和∠BOE是对顶角;
B、∠COE和∠AOD是对顶角;
C、∠BOC和∠AOD是对顶角;
D、∠AOE和∠DOE是对顶角。
2、如右图中直线AB、CD交于O,
OE是∠BOC的平分线且∠BOE=50度,
那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。ABCDOE×√√CC1、一个角的对顶角有 个,邻补角最多有 个,
而补角则可以有 个。一两无数三、填空题2、右图中∠AOC的对顶角是 ,
邻补角是 .∠DOB∠AOD和∠COB3、若∠1与∠2是对顶角,∠1=160,则∠2=______0;
若∠3与∠4是邻补角,则∠3+∠4 =______04、若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3= 05、如图1,∠2与∠3互为邻补角,∠1=∠2,则∠1与∠3的关系为 。图116180180互补归纳小结 对顶
角相
等
邻补
角互
补 ②有公共顶点;③没有公共边①两条直线相交形成的角; ①两条直线相交而成;②有公共顶点;③有一条公共边①都是两条直线相交而成的角;③都是成对出现的 ②都有一个公共顶点;②两直线相交时,
对顶角只有两对
邻补角有四对 ①有无公共边5.1.2 垂线入水姿势特殊情况复习:BACDO1234在相交线的模型中,固定木条a,转动木条b,当α =90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.当α ≠90°时,a与b不垂直,叫斜交.两条直线相交斜交垂直垂直是相交的特殊情况)α abbbbb)α 观察与思考1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。一、垂直的定义日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?十字路口的两条道路围棋盘的横线和竖线铅垂线和水平线图1图4图3图2ba1)图形:Oα 2)文字:a、b互相垂直, 垂足为O3)符号:a⊥b或b⊥a,
若要强调垂足,
则记为:a⊥b, 垂足为O 2.垂直的表示:ABCDO书写形式:如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。①判定:∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式:反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。②性质:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)(∠AOC=∠BOC=∠BOD=90°)3.垂直的书写形式:练习1.两条直线相交所成的四个角中,下列条件中能断定两条直线垂直的是( )
(A)有一个角为90° (B)有两个角相等
(C) 有三个角相等 (D)有四个角相等
(E)有四对邻补角 (F)有一对对顶角互补(G)有一对邻补角相等 (H)有两组角相等 A C D F G练一练如图,已知直线AB、CD都经过O点,OE为射线,
若∠1=35°, ∠2=55°,则OE与AB的位置关系
是 . 切记:要证垂直必先想到直角(90°)联想数学练习2:OE⊥ABACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55° 二、例题例1 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.(对顶角相等)1.在小学学段我们曾通过折纸的方法,得到两条垂线,现在你可以用几种折法得到两条垂线? 想一想 做一做2.如图(5):直线a上有一点A,经过点A,你能折出几条与a垂直的直线?如图(6):直线a外有一点B,经过点B,你能折出几条与a垂直的直线?想一想 做一做过点A、B分别可以做直线a的几条垂线呢?问题:
怎么样画垂线?垂线的画法问题:
这样画l的垂线可以画几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板A无数条1.垂线的画法:lA如图,已知直线 l 和l上的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.1.垂线的画法:lA如图,已知直线 l 和l外的一点A ,作l的垂线.B4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上;则所画直线AB是过点A的直线l的垂线.请同学们画一下1.垂线的画法: 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.垂线的性质(1)①过点P 向线段AB 所在直线引垂线,正确的是( ). A B C D
C练一练练习3.EEE注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.②、练一练练习5、 点O是直线AB上的一点, OC是射线,OE平分∠AOC, OF平分∠BOC,试确定OE与OF的位置关系.并说明理由.练一练1、垂线的定义2、垂线的画法3、垂线的性质(1)过一点有且只有一条直线与已知直线垂直一、放;二、靠;三、移;四、画 小结:
当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
