第三章 代数式 期末复习考点讲义-2024-2025学年数学人教版(2024)七年级上册
文档属性
| 名称 | 第三章 代数式 期末复习考点讲义-2024-2025学年数学人教版(2024)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 280.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 00:00:00 | ||
图片预览



文档简介
第三章 代数式 期末复习考点讲义-2024-2025学年数学人教版(2024)七年级上册
第一步:单元学习目标
1.列代数式表示数量关系 (1)借助现实情境用含字母的式子表示数量和数量关系,进一步理解用字母表示数更具有一般性 (2)能分析具体问题中的简单数量关系,并用代数式表示,体验用数学符号表达数量关系的过程,发展符号意识,形成抽象能力 (3)结合具体情境理解两个量的反比例关系,探索这两个量的变化规律,体会模型思想
2.代数式的值 (1)理解代数式的值的概念,知道当字母取不同的数值时,代数式的值一般也不用,体会从抽象到具体的过程 (2)会把具体数代入代数式进行计算,提高运算能力
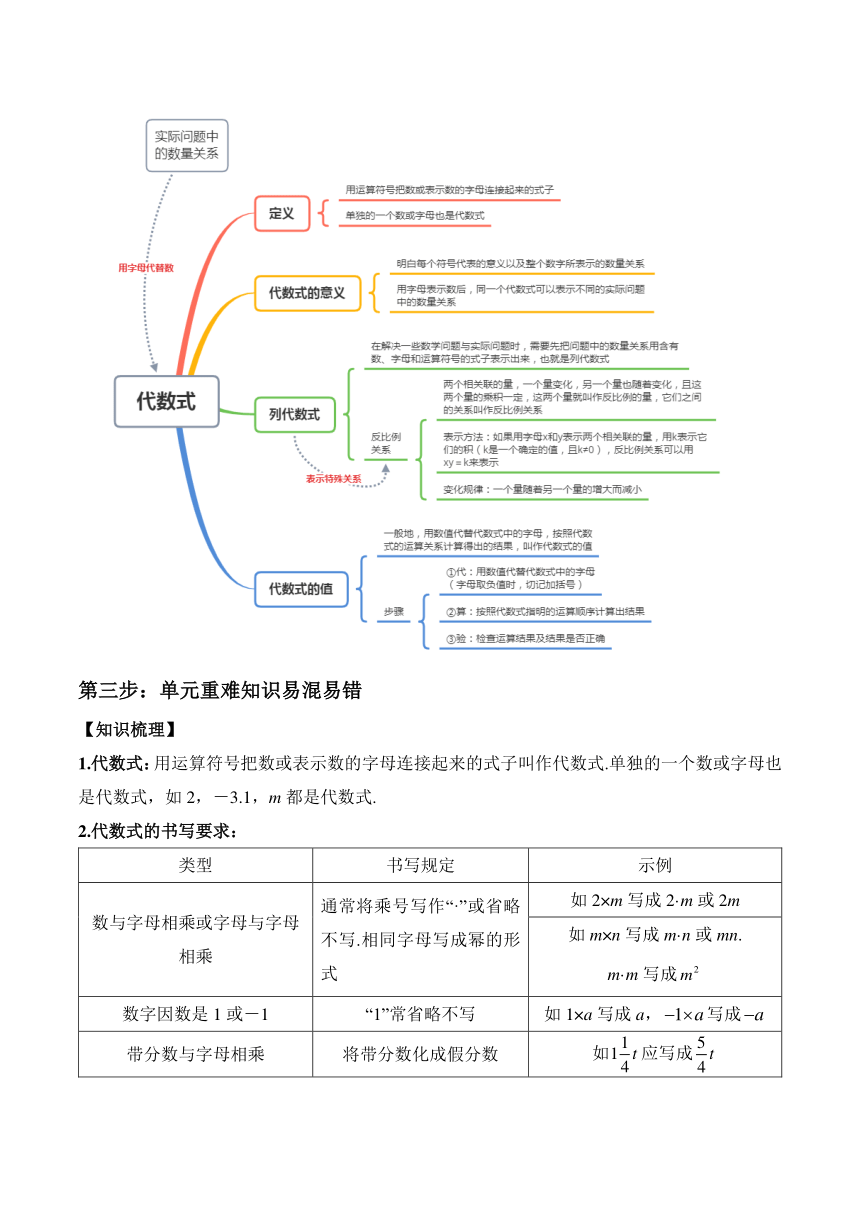
第二步:思维导图回顾知识
第三步:单元重难知识易混易错
【知识梳理】
1.代数式:用运算符号把数或表示数的字母连接起来的式子叫作代数式.单独的一个数或字母也是代数式,如2,-3.1,m都是代数式.
2.代数式的书写要求:
类型 书写规定 示例
数与字母相乘或字母与字母相乘 通常将乘号写作“·”或省略不写.相同字母写成幂的形式 如2×m写成2·m或2m
如m×n写成m·n或mn. m·m写成
数字因数是1或-1 “1”常省略不写 如1×a写成a,写成
带分数与字母相乘 将带分数化成假分数 如应写成
除法运算 用分数线 如应写成
代数式是和或差的形式且后面有单位 把式子用括号括起来 如千克
3.理解代数式的意义:关键在于明白每个符号代表的意义以及整个式子所代表的数量关系.用字母表示数后,同一个代数式可以表示不同的实际问题中的数量关系.
4.列代数式:在解决一些数学问题与实际问题中,需要先把问题中的数量关系用含有数、字母和运算符号的式子表示出来,也就是列代数式.
5.列代数式的步骤:
(1)分析条件,找出数量关系
数学术语 抓住关键性词语,如“大”“小”“多”“少”“和”“差”“积”“商”“倍”等,用数学符号表示.
实际问题中常用的关系式 购买、分配类问题 费用=单位费用×数量;总量=单位量×数量; 总费用=甲的单位费用×甲的数量+乙的单位费用×乙的数量; 总数量=甲的数量+乙的数量 打折销售问题: 售价=标价(原价)×折扣(如打八折,折扣就是80%) 工程问题:总工作量=工作效率×工作时间 行程问题:路程=速度×时间 航行问题: 顺流速度=静水速度+水流速度 逆流速度=静水速度-水流速度 增长率问题: 利息问题:利息=本金×利率×时间
(2)用含有数、字母和运算符号的式子表示数量关系
例:边长为的正方形的面积是
一本笔记本5元,一支钢笔6元,买m本笔记本,n支钢笔,一共需要元
6.反比例关系:两个相关联的量,一个量变化,另一个量也随着变化,且这两个量的乘积一定,两个量就叫作反比例的量,它们之间的关系叫作反比例关系.
7.反比例关系的表示方法:如果用字母和表示两个相关联的量,用表示它们的积(是一个确定的值,且),反比例关系可以用来表示,其中叫作比例系数.
8.两个量的变化规律:一个量随着另一个量的增大而减小.
9.代数式的值:一般地,用数值代替代数式中的字母,按照代数式中的运算关系得出的结果,叫作代数式的值. 当字母取不同的数值时,代数式的值一般也不同.
10.公式的应用:对于有些同类事物中的某种数量关系常常可以用公式来描述,在解决相关问题时,可以用这些公式进行计算.
常用的几何图形公式
三角形 设底边长为,高为,则面积
长方形 设长为,宽为,则周长,面积
圆 设半径为,则周长,面积
长方体 设长为,宽为,高为,则体积
柱体 设底面积为,高为,则体积
圆锥 设底面积为,高为,则体积
【常考题型】
1.下列含有字母的式子.符合书写规范要求的是( )
A. B. C. D.
2.已知,则代数式的值为( )
A.2022 B.2026 C.2028 D.2030
3.参观河南嵩山少林寺的成人门票单价是100元,儿童门票单价是50元.某旅行团有a名成人和b名儿童,则旅行团的门票费用总和为______元(用含a、b的代数式表示).
4.一辆小汽车的速度是a千米/时,一列高铁的速度比这辆小汽车速度的2倍多60千米,则这列高铁的速度是______千米/时.(用含a的代数式表示)
5.如图,在长方形中,,在它内部有三个小正方形,正方形的边长为m,正方形的边长为n.
(1)求图中阴影部分的周长(用含m、n的式子表示);
(2)当,时,求图中阴影部分的周长.
6.某公司将特色农副产品运往邻市市场进行销售,每辆车的平均速度与行驶时间如下表所示:
平均速度 75 80 90
行驶时间
(1)行驶的时间随着平均速度的变化怎样变化?
(2)分别用v(单位:)和t(单位:h)表示平均速度和行驶时间,用式子表示v与t的关系,v与t成什么比例关系?
第四步:单元核心素养对接中考
【核心素养】
(1)符号意识与抽象能力:理解代数式的定义和书写规范,学会用字母表示数和数量关系,将实际问题中的数量关系用代数式表示出来,培养符号意识和抽象能力.
(2)数学建模与应用意识:通过列代数式解决实际问题,如用代数式表示图形的面积、周长等,建立数学模型,提高学生的应用意识和解决实际问题的能力.
(3)逻辑推理与分析能力:在探究代数式的值与字母取值的关系时,需要学生进行逻辑推理和分析,培养逻辑推理与分析能力.
【对接中考】
1.[2024年广东东莞中考真题]已知,则代数式的值为________.
2.[2024年广东广州中考真题]如图,把,,三个电阻串联起来,线路上的电流为I,电压为U,则.当,,,时,U的值为______.
3.[2024年广东广州中考真题]若,则______.
答案以及解析
【常考题型】
1.答案:C
解析:A.,应该写成,故此选项错误;
B.,应该写成,故此选项错误;
C.符合书写规范要求,故此选项正确;
D.,应该写成,故此选项错误;
故选:C.
2.答案:C
解析:,
,
原式.
故选C.
3.答案:
解析:根据题意,旅行团的门票费用总和为:元,
故答案为:.
4.答案:/
解析:根据题意知:高铁的速度是每小时行驶千米.
故答案为:.
5.答案:(1)
(2)36
解析:(1)根据观察可知:图中阴影部分的周长与长为、宽为的矩形周长相同,在场方程中,,,
∵正方形的边长为m,正方形的边长为n,
∴,,
∵,
∴,
∴阴影部分的周长;
(2)当,时,阴影部分的周长.
6.答案:(1)行驶时间随着平均速度的增大而减小
(2)v与t的关系用式子表示为;v与t成反比例关系
解析:(1)观察表格可知,行驶时间随着平均速度的增大而减小.
(2)∵速度×时间=距离,
∴从公司到邻市市场的距离为.
∴v与t的关系用式子表示为.
即v与t成反比例关系.
【对接中考】
1.答案:3
解析:
故答案为:3.
2.答案:220
解析:,
当,,,时,
,
故答案为:220.
3.答案:11
解析:,
,
,
故答案为:11.
第一步:单元学习目标
1.列代数式表示数量关系 (1)借助现实情境用含字母的式子表示数量和数量关系,进一步理解用字母表示数更具有一般性 (2)能分析具体问题中的简单数量关系,并用代数式表示,体验用数学符号表达数量关系的过程,发展符号意识,形成抽象能力 (3)结合具体情境理解两个量的反比例关系,探索这两个量的变化规律,体会模型思想
2.代数式的值 (1)理解代数式的值的概念,知道当字母取不同的数值时,代数式的值一般也不用,体会从抽象到具体的过程 (2)会把具体数代入代数式进行计算,提高运算能力
第二步:思维导图回顾知识
第三步:单元重难知识易混易错
【知识梳理】
1.代数式:用运算符号把数或表示数的字母连接起来的式子叫作代数式.单独的一个数或字母也是代数式,如2,-3.1,m都是代数式.
2.代数式的书写要求:
类型 书写规定 示例
数与字母相乘或字母与字母相乘 通常将乘号写作“·”或省略不写.相同字母写成幂的形式 如2×m写成2·m或2m
如m×n写成m·n或mn. m·m写成
数字因数是1或-1 “1”常省略不写 如1×a写成a,写成
带分数与字母相乘 将带分数化成假分数 如应写成
除法运算 用分数线 如应写成
代数式是和或差的形式且后面有单位 把式子用括号括起来 如千克
3.理解代数式的意义:关键在于明白每个符号代表的意义以及整个式子所代表的数量关系.用字母表示数后,同一个代数式可以表示不同的实际问题中的数量关系.
4.列代数式:在解决一些数学问题与实际问题中,需要先把问题中的数量关系用含有数、字母和运算符号的式子表示出来,也就是列代数式.
5.列代数式的步骤:
(1)分析条件,找出数量关系
数学术语 抓住关键性词语,如“大”“小”“多”“少”“和”“差”“积”“商”“倍”等,用数学符号表示.
实际问题中常用的关系式 购买、分配类问题 费用=单位费用×数量;总量=单位量×数量; 总费用=甲的单位费用×甲的数量+乙的单位费用×乙的数量; 总数量=甲的数量+乙的数量 打折销售问题: 售价=标价(原价)×折扣(如打八折,折扣就是80%) 工程问题:总工作量=工作效率×工作时间 行程问题:路程=速度×时间 航行问题: 顺流速度=静水速度+水流速度 逆流速度=静水速度-水流速度 增长率问题: 利息问题:利息=本金×利率×时间
(2)用含有数、字母和运算符号的式子表示数量关系
例:边长为的正方形的面积是
一本笔记本5元,一支钢笔6元,买m本笔记本,n支钢笔,一共需要元
6.反比例关系:两个相关联的量,一个量变化,另一个量也随着变化,且这两个量的乘积一定,两个量就叫作反比例的量,它们之间的关系叫作反比例关系.
7.反比例关系的表示方法:如果用字母和表示两个相关联的量,用表示它们的积(是一个确定的值,且),反比例关系可以用来表示,其中叫作比例系数.
8.两个量的变化规律:一个量随着另一个量的增大而减小.
9.代数式的值:一般地,用数值代替代数式中的字母,按照代数式中的运算关系得出的结果,叫作代数式的值. 当字母取不同的数值时,代数式的值一般也不同.
10.公式的应用:对于有些同类事物中的某种数量关系常常可以用公式来描述,在解决相关问题时,可以用这些公式进行计算.
常用的几何图形公式
三角形 设底边长为,高为,则面积
长方形 设长为,宽为,则周长,面积
圆 设半径为,则周长,面积
长方体 设长为,宽为,高为,则体积
柱体 设底面积为,高为,则体积
圆锥 设底面积为,高为,则体积
【常考题型】
1.下列含有字母的式子.符合书写规范要求的是( )
A. B. C. D.
2.已知,则代数式的值为( )
A.2022 B.2026 C.2028 D.2030
3.参观河南嵩山少林寺的成人门票单价是100元,儿童门票单价是50元.某旅行团有a名成人和b名儿童,则旅行团的门票费用总和为______元(用含a、b的代数式表示).
4.一辆小汽车的速度是a千米/时,一列高铁的速度比这辆小汽车速度的2倍多60千米,则这列高铁的速度是______千米/时.(用含a的代数式表示)
5.如图,在长方形中,,在它内部有三个小正方形,正方形的边长为m,正方形的边长为n.
(1)求图中阴影部分的周长(用含m、n的式子表示);
(2)当,时,求图中阴影部分的周长.
6.某公司将特色农副产品运往邻市市场进行销售,每辆车的平均速度与行驶时间如下表所示:
平均速度 75 80 90
行驶时间
(1)行驶的时间随着平均速度的变化怎样变化?
(2)分别用v(单位:)和t(单位:h)表示平均速度和行驶时间,用式子表示v与t的关系,v与t成什么比例关系?
第四步:单元核心素养对接中考
【核心素养】
(1)符号意识与抽象能力:理解代数式的定义和书写规范,学会用字母表示数和数量关系,将实际问题中的数量关系用代数式表示出来,培养符号意识和抽象能力.
(2)数学建模与应用意识:通过列代数式解决实际问题,如用代数式表示图形的面积、周长等,建立数学模型,提高学生的应用意识和解决实际问题的能力.
(3)逻辑推理与分析能力:在探究代数式的值与字母取值的关系时,需要学生进行逻辑推理和分析,培养逻辑推理与分析能力.
【对接中考】
1.[2024年广东东莞中考真题]已知,则代数式的值为________.
2.[2024年广东广州中考真题]如图,把,,三个电阻串联起来,线路上的电流为I,电压为U,则.当,,,时,U的值为______.
3.[2024年广东广州中考真题]若,则______.
答案以及解析
【常考题型】
1.答案:C
解析:A.,应该写成,故此选项错误;
B.,应该写成,故此选项错误;
C.符合书写规范要求,故此选项正确;
D.,应该写成,故此选项错误;
故选:C.
2.答案:C
解析:,
,
原式.
故选C.
3.答案:
解析:根据题意,旅行团的门票费用总和为:元,
故答案为:.
4.答案:/
解析:根据题意知:高铁的速度是每小时行驶千米.
故答案为:.
5.答案:(1)
(2)36
解析:(1)根据观察可知:图中阴影部分的周长与长为、宽为的矩形周长相同,在场方程中,,,
∵正方形的边长为m,正方形的边长为n,
∴,,
∵,
∴,
∴阴影部分的周长;
(2)当,时,阴影部分的周长.
6.答案:(1)行驶时间随着平均速度的增大而减小
(2)v与t的关系用式子表示为;v与t成反比例关系
解析:(1)观察表格可知,行驶时间随着平均速度的增大而减小.
(2)∵速度×时间=距离,
∴从公司到邻市市场的距离为.
∴v与t的关系用式子表示为.
即v与t成反比例关系.
【对接中考】
1.答案:3
解析:
故答案为:3.
2.答案:220
解析:,
当,,,时,
,
故答案为:220.
3.答案:11
解析:,
,
,
故答案为:11.
同课章节目录
