第二十三章 旋转 期末复习考点讲义-2024-2025学年数学人教版(2012)九年级上册
文档属性
| 名称 | 第二十三章 旋转 期末复习考点讲义-2024-2025学年数学人教版(2012)九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 21:10:25 | ||
图片预览

文档简介
第二十三章 旋转 期末复习考点讲义-2024-2025学年数学人教版(2012)九年级上册
第一步:单元学习目标
1.图形的旋转 (1)了解平面图形旋转的概念,能指出某一图形旋转时的旋转中心、旋转方向和旋转角 (2)探究并理解旋转的性质,并会运用其性质解决简单的旋转问题 (3)会按要求作出旋转后的图形
2.中心对称 (1)了解中心对称、中心对称图形的概念,并明确它们之间的区别与联系 (2)探究并掌握中心对称的性质,会画已知图形关于已知点成中心对称的图形 (3)掌握关于原点对称的点的坐标特征,能画已知图形关于原点对称的图形
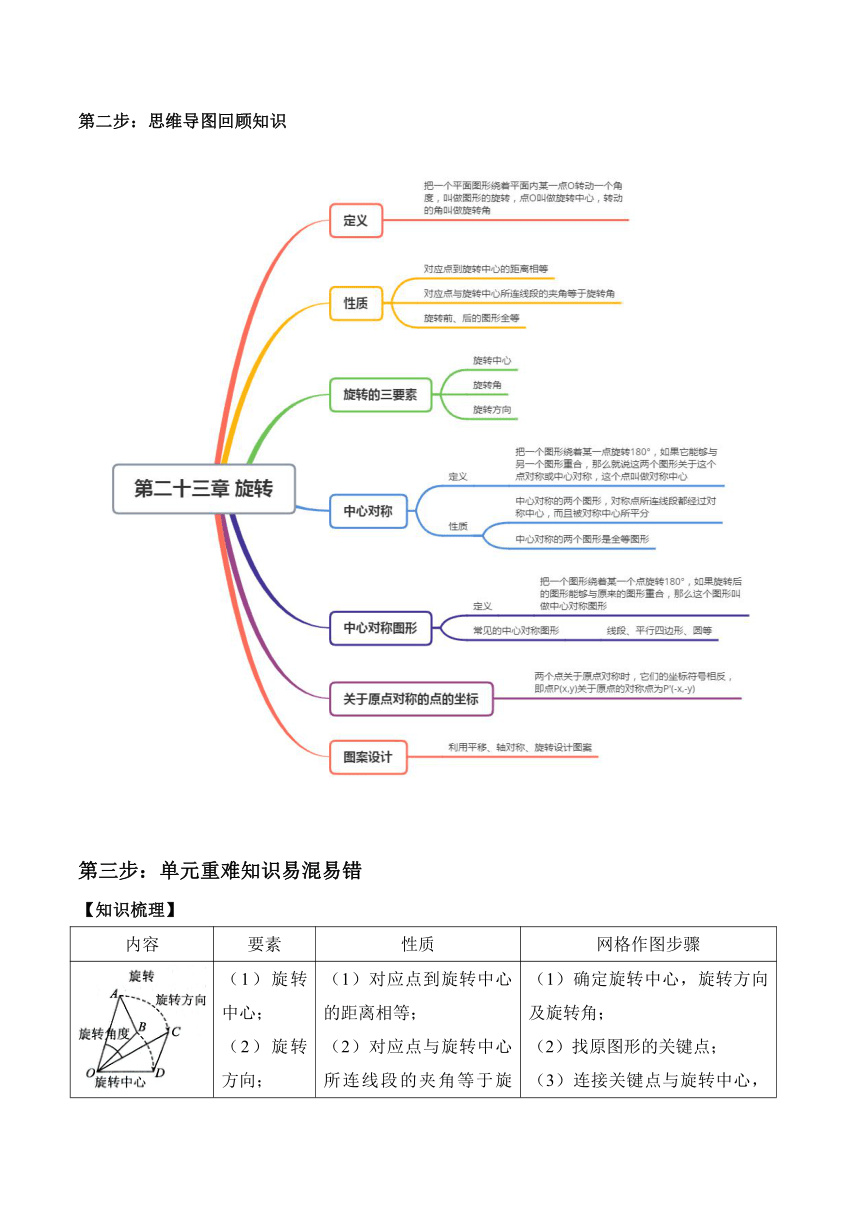
第二步:思维导图回顾知识
第三步:单元重难知识易混易错
【知识梳理】
内容 要素 性质 网格作图步骤
(1)旋转中心; (2)旋转方向; (3)旋转角度 (1)对应点到旋转中心的距离相等; (2)对应点与旋转中心所连线段的夹角等于旋转角; (3)旋转前后的图形全等 (1)确定旋转中心,旋转方向及旋转角; (2)找原图形的关键点; (3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点; (4)按原图形顺次连接各关键点旋转后的对应点,得到旋转后的图形
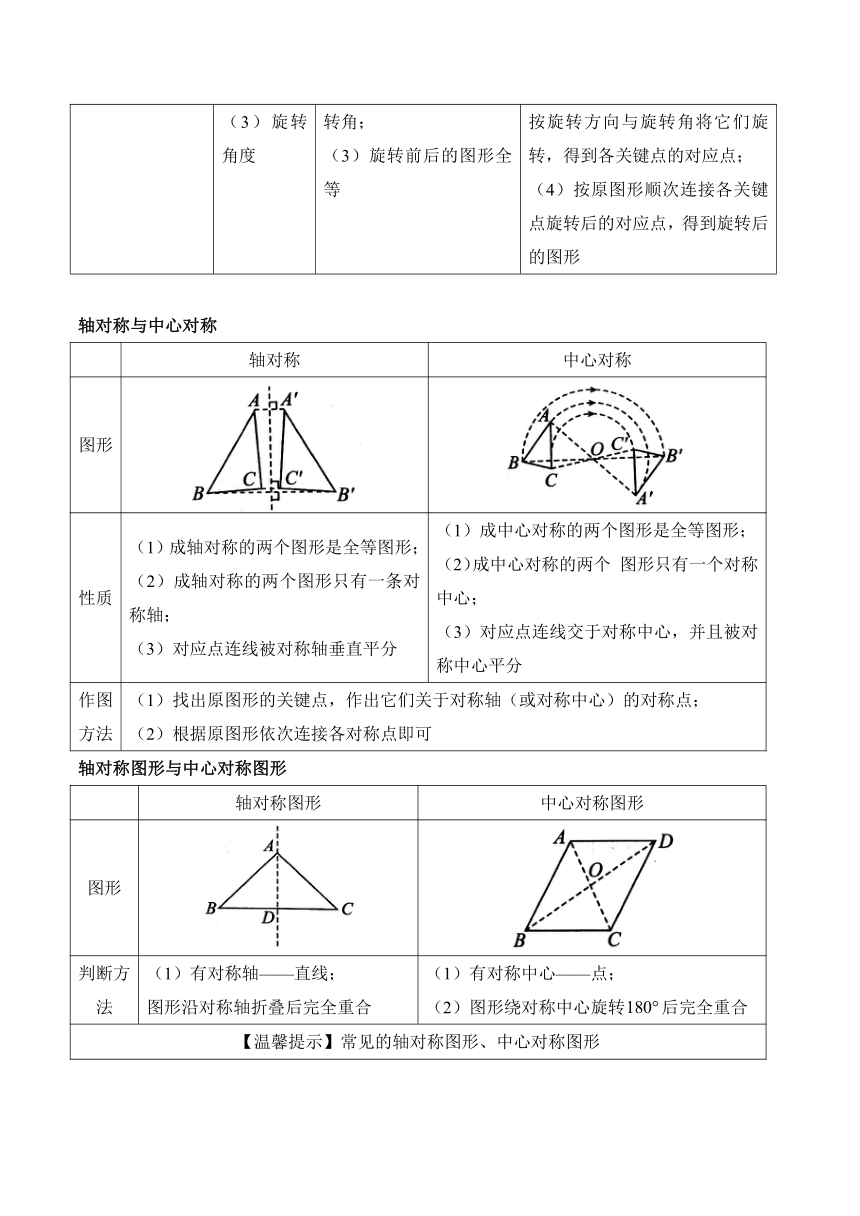
轴对称与中心对称
轴对称 中心对称
图形
性质 (1)成轴对称的两个图形是全等图形; (2)成轴对称的两个图形只有一条对称轴; (3)对应点连线被对称轴垂直平分 (1)成中心对称的两个图形是全等图形; (2)成中心对称的两个 图形只有一个对称中心; (3)对应点连线交于对称中心,并且被对称中心平分
作图方法 (1)找出原图形的关键点,作出它们关于对称轴(或对称中心)的对称点; (2)根据原图形依次连接各对称点即可
轴对称图形与中心对称图形
轴对称图形 中心对称图形
图形
判断方法 (1)有对称轴——直线; 图形沿对称轴折叠后完全重合 (1)有对称中心——点; (2)图形绕对称中心旋转后完全重合
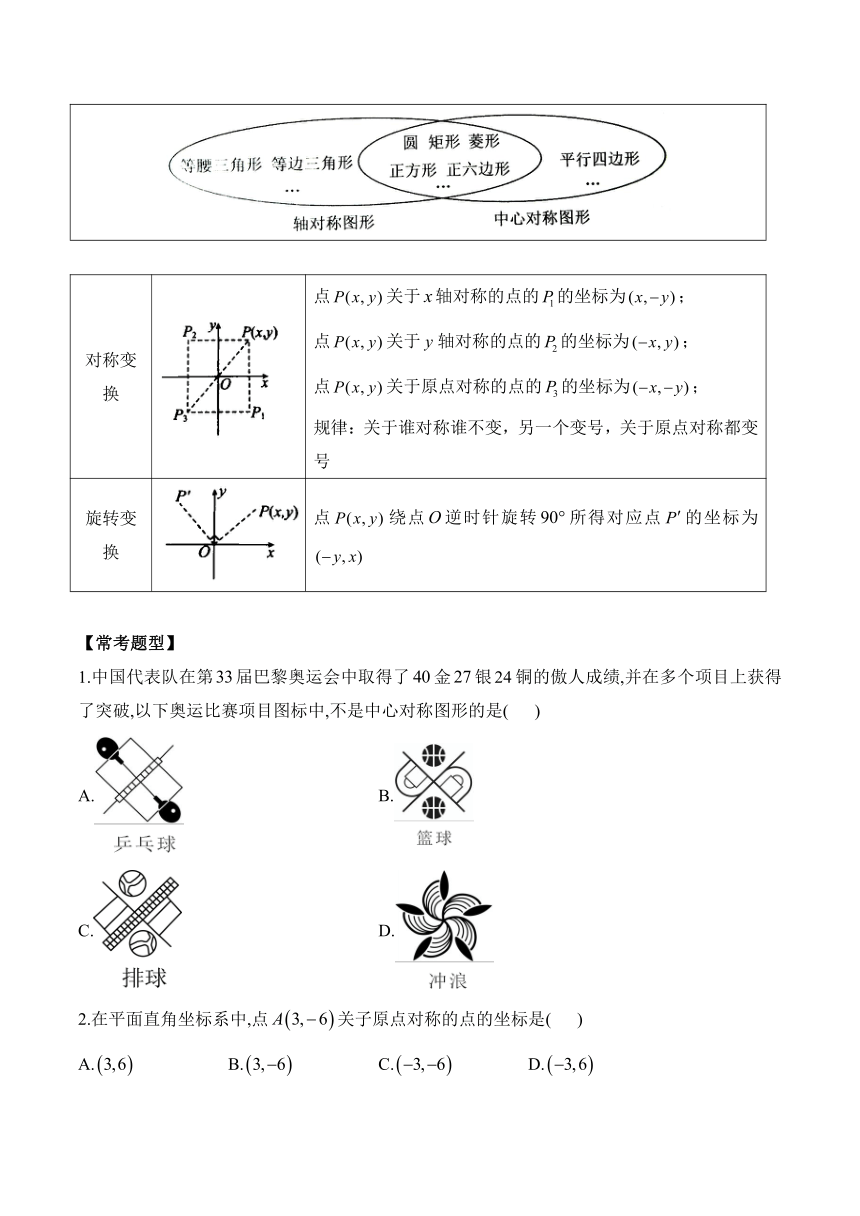
【温馨提示】常见的轴对称图形、中心对称图形
对称变换 点关于轴对称的点的的坐标为; 点关于轴对称的点的的坐标为; 点关于原点对称的点的的坐标为; 规律:关于谁对称谁不变,另一个变号,关于原点对称都变号
旋转变换 点绕点逆时针旋转所得对应点的坐标为
【常考题型】
1.中国代表队在第届巴黎奥运会中取得了金银铜的傲人成绩,并在多个项目上获得了突破,以下奥运比赛项目图标中,不是中心对称图形的是( )
A. B.
C. D.
2.在平面直角坐标系中,点关子原点对称的点的坐标是( )
A. B. C. D.
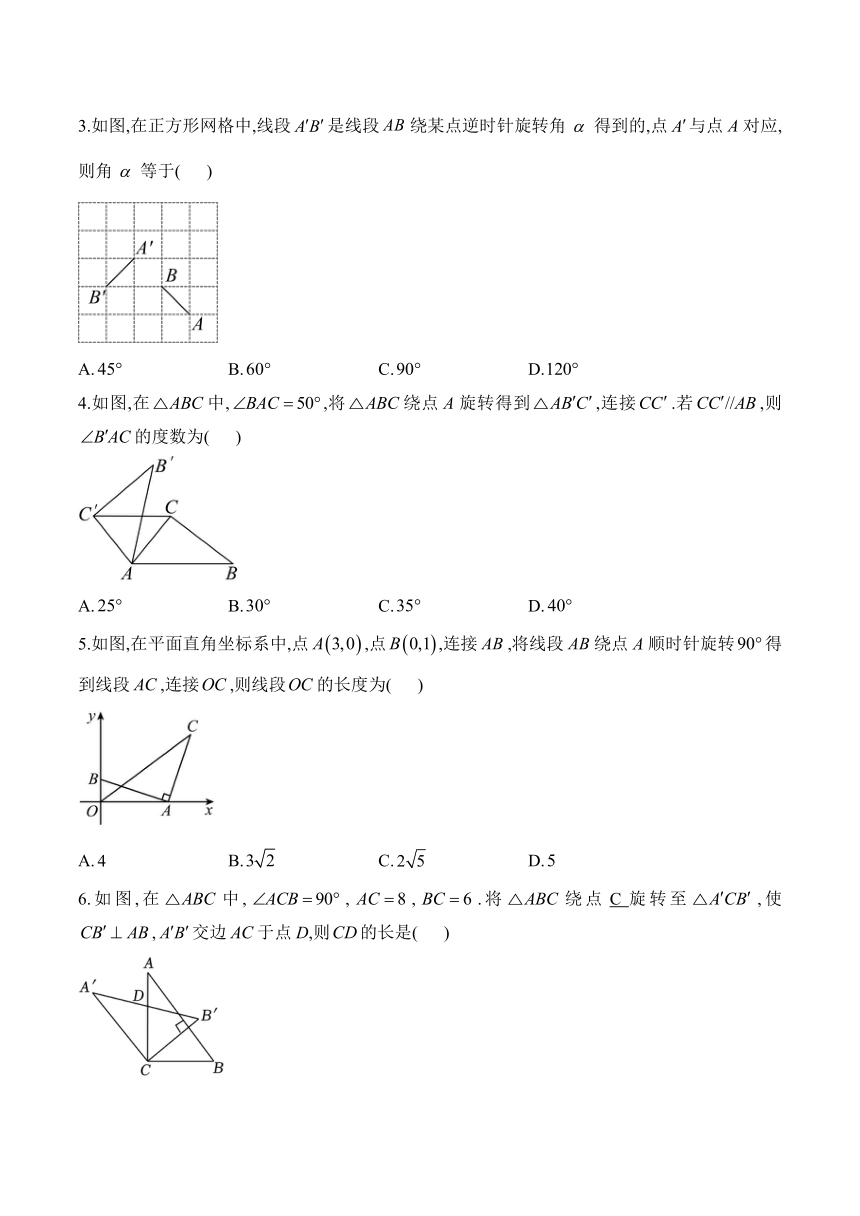
3.如图,在正方形网格中,线段是线段绕某点逆时针旋转角得到的,点与点A对应,则角等于( )
A. B. C. D.
4.如图,在中,,将绕点A旋转得到,连接.若,则的度数为( )
A. B. C. D.
5.如图,在平面直角坐标系中,点,点,连接,将线段绕点A顺时针旋转得到线段,连接,则线段的长度为( )
A. B. C. D.
6.如图,在中,,,.将绕点C旋转至,使,交边于点D,则的长是( )
A.4 B. C.5 D.6
7.在下面的网格图中,每个小正方形的边长均为1个单位长度.在中,,,.
(1)在图中作出以点A为旋转中心,沿顺时针方向旋转后的图形.
(2)若点A的坐标为,点B的坐标为,请在图中画出平面直角坐标系,并写出点C的坐标.
(3)根据(2)中的平面直角坐标系,作出与关于原点对称的.
第四步:单元核心素养对接中考
【核心素养】
(1)空间观念:要求学生在脑海中模拟图形旋转的过程,包括旋转的方向、角度以及旋转后的位置关系,培养空间观念.
(2)几何直观与抽象概括:通过观察具体的旋转实例,直观感受旋转的特征,进而抽象概括出旋转的概念和性质,培养几何直观和抽象概括能力.
(3)逻辑推理与探究能力:在探究旋转的性质和应用的过程中,需要学生进行推理和证明,以及通过探究活动发现规律,培养逻辑推理和探究能力.
【对接中考】
一、单选题
1.[2024年黑龙江哈尔滨中考真题]剪纸是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.[2024年广东广州中考真题]下列图案中,点O为正方形的中心,阴影部分的两个三角形全等,则阴影部分的两个三角形关于点O对称的是( )
A. B. C. D.
3.[2024年湖北中考真题]平面坐标系中,点A的坐标为,将线段绕点O顺时针旋转,则点A的对应点的坐标为( )
A. B. C. D.
4.[2024年吉林中考真题]如图,在平面直角坐标系中,点A的坐标为,点C的坐标为.以,为边作矩形,若将矩形绕点O顺时针旋转,得到矩形,则点的坐标为( )
A. B. C. D.
5.[2024年天津中考真题]如图,中,,将绕点C顺时针旋转得到,点A,B的对应点分别为D,E,延长交于点F,下列结论一定正确的是( )
A. B.
C. D.
6.[2024年湖北武汉中考真题]如图,小好同学用计算机软件绘制函数的图象,发现它关于点中心对称.若点,,,……,,都在函数图象上,这个点的横坐标从开始依次增加,则的值是( )
A. B. C.0 D.1
7.[2024年北京中考真题]如图,在菱形中,,O为对角线的交点.将菱形绕点O逆时针旋转得到菱形,两个菱形的公共点为E,F,G,H.对八边形给出下面四个结论:
①该八边形各边长都相等;
②该八边形各内角都相等;
③点O到该八边形各顶点的距离都相等;
④点O到该八边形各边所在直线的距离都相等.
上述结论中,所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
8.[2024年安徽中考真题]如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,格点(网格线的交点)A、B,C、D的坐标分别为,,,.
(1)以点D为旋转中心,将旋转得到,画出;
(2)直接写出以B,,,C为顶点的四边形的面积;
(3)在所给的网格图中确定一个格点E,使得射线平分,写出点E的坐标.
9.[2024年山西中考真题]综合与探究
问题情境:如图1,四边形ABCD是菱形,过点A作于点E,过点C作于点F.
猜想证明:(1)判断四边形AECF的形状,并说明理由;
深入探究:(2)将图1中的绕点A逆时针旋转,得到,点E,B的对应点分别为点G,H.
①如图2,当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.猜想线段CH与MD的数量关系,并说明理由;
②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点Q.若,直接写出四边形AMNQ的面积.
答案以及解析
【常考题型】
1.答案:D
解析:A.图形是中心对称图形,故本选项不符合题意;
B.图形是中心对称图形,故本选项不符合题意.
C.图形是中心对称图形,故本选项不符合题意;
D.图形不是中心对称图形,故本选项符合题意;
故选:D.
2.答案:D
解析:点关子原点对称的点的坐标是,
故选:D.
3.答案:C
解析:∵点A的对应点为点,点B的对应点为点,且对应点到旋转中心的距离相等,
∴旋转中心为线段和线段的垂直平分线的交点.
如图,作线段和线段的垂直平分线,其交点O为旋转中心.
连接,.
根据旋转的性质,得
.
故选:C.
4.答案:B
解析:∵,
.
由旋转,得,,
.
.
.
故选B.
5.答案:D
解析:如图所示,过点C作轴于点D,
∵点,点,
∴,,
∵将线段绕点A顺时针旋转得到线段,
∴,,且,
∴,,
∴,
在,中,
,
∴,
∴,,
∴,
∴点D的坐标为,
∴在中,,
故选:D.
6.答案:C
解析:∵将绕点C旋转至,
∴,,,
∵,
∴,
∴,
∴,
∴,
而,
∴,
∴,
∴.
故选:C.
7.答案:(1)见解析
(2)建立平面直角坐标系见解析.点C的坐标为
(3)见解析
解析:(1)如图,即为所求.
(2)建立平面直角坐标系如图所示.点C的坐标为.
(3)如图,即为所求.
【对接中考】
1.答案:D
解析:A.图形既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.图形是中心对称图形,但不是轴对称图形,故此选项不合题意;
C.图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
D.图形既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
2.答案:C
解析:由图形可知,阴影部分的两个三角形关于点O对称的是C,
故选:C.
3.答案:B
解析:过点A和点分别作x轴的垂线,垂足分别为B,C,
点A的坐标为,
,,
将线段绕点O顺时针旋转得到,
,,
,
,
,,
点的坐标为,
故选:B.
4.答案:C
解析:点A的坐标为,点C的坐标为,
,,
四边形矩形,
,,
将矩形绕点O顺时针旋转,得到矩形,
,,,
轴,
点的坐标为,
故选:C.
5.答案:D
解析:设与相交于点H,如图所示:
中,将绕点C顺时针旋转得到,
,
,
在中,
,
,故D选项正确;
设,
,
,
,
,
不一定等于,
不一定等于,
不一定成立,故B选项不正确;
,,不一定等于,
不一定成立,故A选项不正确;
将绕点C顺时针旋转得到,
,故C选项不正确;
故选:D.
6.答案:D
解析:这个点的横坐标从开始依次增加,
,
,
,而即,
,
当时,,即,
关于点中心对称的点为,
即当时,,
,
故选:D.
7.答案:B
解析:向两方分别延长,连接,
根据菱形,,则,,
菱形绕点O逆时针旋转得到菱形,
点,,,一定在对角线,上,且,,
,,
,
,
,,同理可证,,,
,,,
,
,
,
该八边形各边长都相等,
故①正确;
根据角的平分线的性质定理,得点O到该八边形各边所在直线的距离都相等,
④正确;
根据题意,得,
,,
,
该八边形各内角不相等;
②错误,
根据,,,
,
,,
故,
点O到该八边形各顶点的距离都相等错误
③错误,
故选B.
8.答案:(1)见详解
(2)40
(3)(答案不唯一)
解析:(1)如图,画出;
(2)以B,,,C为顶点的四边形的面积
.
(3)如图,点E即为所求(答案不唯一),点E的坐标.
9.答案:(1)矩形
(2)①;②或
解析:(1)四边形AECF为矩形.
理由如下:,,
,.
四边形ABCD为菱形,,.
.
四边形AECF为矩形.
(2)①.
理由如下:
证法一:四边形ABCD为菱形,,.
旋转得到,
,.
,.
,.
,.
.
证法二:如图,连接HD.
四边形ABCD为菱形,,.
旋转得到,
,.
,.
.
.
.
,.
.
②或.
第一步:单元学习目标
1.图形的旋转 (1)了解平面图形旋转的概念,能指出某一图形旋转时的旋转中心、旋转方向和旋转角 (2)探究并理解旋转的性质,并会运用其性质解决简单的旋转问题 (3)会按要求作出旋转后的图形
2.中心对称 (1)了解中心对称、中心对称图形的概念,并明确它们之间的区别与联系 (2)探究并掌握中心对称的性质,会画已知图形关于已知点成中心对称的图形 (3)掌握关于原点对称的点的坐标特征,能画已知图形关于原点对称的图形
第二步:思维导图回顾知识
第三步:单元重难知识易混易错
【知识梳理】
内容 要素 性质 网格作图步骤
(1)旋转中心; (2)旋转方向; (3)旋转角度 (1)对应点到旋转中心的距离相等; (2)对应点与旋转中心所连线段的夹角等于旋转角; (3)旋转前后的图形全等 (1)确定旋转中心,旋转方向及旋转角; (2)找原图形的关键点; (3)连接关键点与旋转中心,按旋转方向与旋转角将它们旋转,得到各关键点的对应点; (4)按原图形顺次连接各关键点旋转后的对应点,得到旋转后的图形
轴对称与中心对称
轴对称 中心对称
图形
性质 (1)成轴对称的两个图形是全等图形; (2)成轴对称的两个图形只有一条对称轴; (3)对应点连线被对称轴垂直平分 (1)成中心对称的两个图形是全等图形; (2)成中心对称的两个 图形只有一个对称中心; (3)对应点连线交于对称中心,并且被对称中心平分
作图方法 (1)找出原图形的关键点,作出它们关于对称轴(或对称中心)的对称点; (2)根据原图形依次连接各对称点即可
轴对称图形与中心对称图形
轴对称图形 中心对称图形
图形
判断方法 (1)有对称轴——直线; 图形沿对称轴折叠后完全重合 (1)有对称中心——点; (2)图形绕对称中心旋转后完全重合
【温馨提示】常见的轴对称图形、中心对称图形
对称变换 点关于轴对称的点的的坐标为; 点关于轴对称的点的的坐标为; 点关于原点对称的点的的坐标为; 规律:关于谁对称谁不变,另一个变号,关于原点对称都变号
旋转变换 点绕点逆时针旋转所得对应点的坐标为
【常考题型】
1.中国代表队在第届巴黎奥运会中取得了金银铜的傲人成绩,并在多个项目上获得了突破,以下奥运比赛项目图标中,不是中心对称图形的是( )
A. B.
C. D.
2.在平面直角坐标系中,点关子原点对称的点的坐标是( )
A. B. C. D.
3.如图,在正方形网格中,线段是线段绕某点逆时针旋转角得到的,点与点A对应,则角等于( )
A. B. C. D.
4.如图,在中,,将绕点A旋转得到,连接.若,则的度数为( )
A. B. C. D.
5.如图,在平面直角坐标系中,点,点,连接,将线段绕点A顺时针旋转得到线段,连接,则线段的长度为( )
A. B. C. D.
6.如图,在中,,,.将绕点C旋转至,使,交边于点D,则的长是( )
A.4 B. C.5 D.6
7.在下面的网格图中,每个小正方形的边长均为1个单位长度.在中,,,.
(1)在图中作出以点A为旋转中心,沿顺时针方向旋转后的图形.
(2)若点A的坐标为,点B的坐标为,请在图中画出平面直角坐标系,并写出点C的坐标.
(3)根据(2)中的平面直角坐标系,作出与关于原点对称的.
第四步:单元核心素养对接中考
【核心素养】
(1)空间观念:要求学生在脑海中模拟图形旋转的过程,包括旋转的方向、角度以及旋转后的位置关系,培养空间观念.
(2)几何直观与抽象概括:通过观察具体的旋转实例,直观感受旋转的特征,进而抽象概括出旋转的概念和性质,培养几何直观和抽象概括能力.
(3)逻辑推理与探究能力:在探究旋转的性质和应用的过程中,需要学生进行推理和证明,以及通过探究活动发现规律,培养逻辑推理和探究能力.
【对接中考】
一、单选题
1.[2024年黑龙江哈尔滨中考真题]剪纸是我国最古老的民间艺术之一.下列剪纸图案中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.[2024年广东广州中考真题]下列图案中,点O为正方形的中心,阴影部分的两个三角形全等,则阴影部分的两个三角形关于点O对称的是( )
A. B. C. D.
3.[2024年湖北中考真题]平面坐标系中,点A的坐标为,将线段绕点O顺时针旋转,则点A的对应点的坐标为( )
A. B. C. D.
4.[2024年吉林中考真题]如图,在平面直角坐标系中,点A的坐标为,点C的坐标为.以,为边作矩形,若将矩形绕点O顺时针旋转,得到矩形,则点的坐标为( )
A. B. C. D.
5.[2024年天津中考真题]如图,中,,将绕点C顺时针旋转得到,点A,B的对应点分别为D,E,延长交于点F,下列结论一定正确的是( )
A. B.
C. D.
6.[2024年湖北武汉中考真题]如图,小好同学用计算机软件绘制函数的图象,发现它关于点中心对称.若点,,,……,,都在函数图象上,这个点的横坐标从开始依次增加,则的值是( )
A. B. C.0 D.1
7.[2024年北京中考真题]如图,在菱形中,,O为对角线的交点.将菱形绕点O逆时针旋转得到菱形,两个菱形的公共点为E,F,G,H.对八边形给出下面四个结论:
①该八边形各边长都相等;
②该八边形各内角都相等;
③点O到该八边形各顶点的距离都相等;
④点O到该八边形各边所在直线的距离都相等.
上述结论中,所有正确结论的序号是( )
A.①③ B.①④ C.②③ D.②④
8.[2024年安徽中考真题]如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系,格点(网格线的交点)A、B,C、D的坐标分别为,,,.
(1)以点D为旋转中心,将旋转得到,画出;
(2)直接写出以B,,,C为顶点的四边形的面积;
(3)在所给的网格图中确定一个格点E,使得射线平分,写出点E的坐标.
9.[2024年山西中考真题]综合与探究
问题情境:如图1,四边形ABCD是菱形,过点A作于点E,过点C作于点F.
猜想证明:(1)判断四边形AECF的形状,并说明理由;
深入探究:(2)将图1中的绕点A逆时针旋转,得到,点E,B的对应点分别为点G,H.
①如图2,当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.猜想线段CH与MD的数量关系,并说明理由;
②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点Q.若,直接写出四边形AMNQ的面积.
答案以及解析
【常考题型】
1.答案:D
解析:A.图形是中心对称图形,故本选项不符合题意;
B.图形是中心对称图形,故本选项不符合题意.
C.图形是中心对称图形,故本选项不符合题意;
D.图形不是中心对称图形,故本选项符合题意;
故选:D.
2.答案:D
解析:点关子原点对称的点的坐标是,
故选:D.
3.答案:C
解析:∵点A的对应点为点,点B的对应点为点,且对应点到旋转中心的距离相等,
∴旋转中心为线段和线段的垂直平分线的交点.
如图,作线段和线段的垂直平分线,其交点O为旋转中心.
连接,.
根据旋转的性质,得
.
故选:C.
4.答案:B
解析:∵,
.
由旋转,得,,
.
.
.
故选B.
5.答案:D
解析:如图所示,过点C作轴于点D,
∵点,点,
∴,,
∵将线段绕点A顺时针旋转得到线段,
∴,,且,
∴,,
∴,
在,中,
,
∴,
∴,,
∴,
∴点D的坐标为,
∴在中,,
故选:D.
6.答案:C
解析:∵将绕点C旋转至,
∴,,,
∵,
∴,
∴,
∴,
∴,
而,
∴,
∴,
∴.
故选:C.
7.答案:(1)见解析
(2)建立平面直角坐标系见解析.点C的坐标为
(3)见解析
解析:(1)如图,即为所求.
(2)建立平面直角坐标系如图所示.点C的坐标为.
(3)如图,即为所求.
【对接中考】
1.答案:D
解析:A.图形既不是轴对称图形,也不是中心对称图形,故此选项不符合题意;
B.图形是中心对称图形,但不是轴对称图形,故此选项不合题意;
C.图形是轴对称图形,但不是中心对称图形,故此选项不合题意;
D.图形既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
2.答案:C
解析:由图形可知,阴影部分的两个三角形关于点O对称的是C,
故选:C.
3.答案:B
解析:过点A和点分别作x轴的垂线,垂足分别为B,C,
点A的坐标为,
,,
将线段绕点O顺时针旋转得到,
,,
,
,
,,
点的坐标为,
故选:B.
4.答案:C
解析:点A的坐标为,点C的坐标为,
,,
四边形矩形,
,,
将矩形绕点O顺时针旋转,得到矩形,
,,,
轴,
点的坐标为,
故选:C.
5.答案:D
解析:设与相交于点H,如图所示:
中,将绕点C顺时针旋转得到,
,
,
在中,
,
,故D选项正确;
设,
,
,
,
,
不一定等于,
不一定等于,
不一定成立,故B选项不正确;
,,不一定等于,
不一定成立,故A选项不正确;
将绕点C顺时针旋转得到,
,故C选项不正确;
故选:D.
6.答案:D
解析:这个点的横坐标从开始依次增加,
,
,
,而即,
,
当时,,即,
关于点中心对称的点为,
即当时,,
,
故选:D.
7.答案:B
解析:向两方分别延长,连接,
根据菱形,,则,,
菱形绕点O逆时针旋转得到菱形,
点,,,一定在对角线,上,且,,
,,
,
,
,,同理可证,,,
,,,
,
,
,
该八边形各边长都相等,
故①正确;
根据角的平分线的性质定理,得点O到该八边形各边所在直线的距离都相等,
④正确;
根据题意,得,
,,
,
该八边形各内角不相等;
②错误,
根据,,,
,
,,
故,
点O到该八边形各顶点的距离都相等错误
③错误,
故选B.
8.答案:(1)见详解
(2)40
(3)(答案不唯一)
解析:(1)如图,画出;
(2)以B,,,C为顶点的四边形的面积
.
(3)如图,点E即为所求(答案不唯一),点E的坐标.
9.答案:(1)矩形
(2)①;②或
解析:(1)四边形AECF为矩形.
理由如下:,,
,.
四边形ABCD为菱形,,.
.
四边形AECF为矩形.
(2)①.
理由如下:
证法一:四边形ABCD为菱形,,.
旋转得到,
,.
,.
,.
,.
.
证法二:如图,连接HD.
四边形ABCD为菱形,,.
旋转得到,
,.
,.
.
.
.
,.
.
②或.
同课章节目录
