1.2直角三角形 第1课时 直角三角形的性质与判定 课件(共19张PPT)
文档属性
| 名称 | 1.2直角三角形 第1课时 直角三角形的性质与判定 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
1.2 直角三角形
第1课时 直角三角形的性质与判定
1. 复习直角三角形的相关知识,归纳并掌握直角三角形的性质和判定;(重点)
2. 学习并掌握勾股定理及其逆定理,能够运用其解决问题.(难点)
直角三角形的两个锐角互余.
问题1 直角三角形的定义是什么?
问题2 三角形内角和的性质是什么?
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
这节课我们一起来证明直角三角形的判定与性质.
问题3 前面我们探究过直角三角形的哪些性质?
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
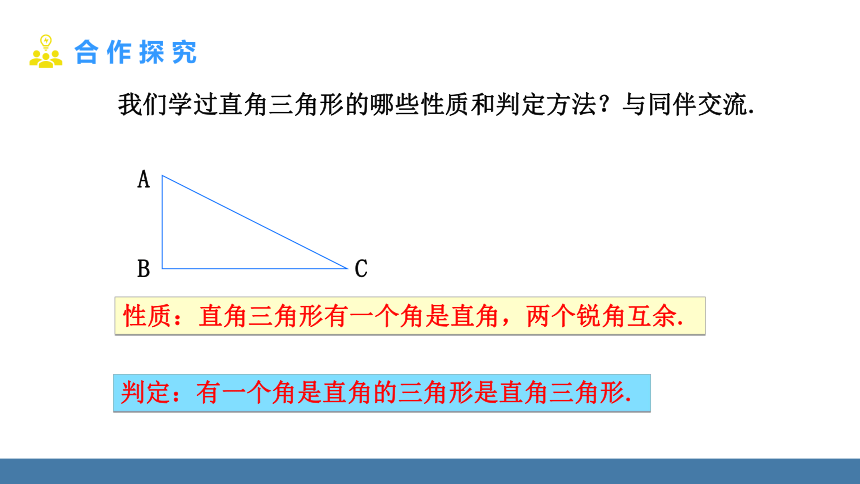
我们学过直角三角形的哪些性质和判定方法?与同伴交流.
A
B
C
性质:直角三角形有一个角是直角,两个锐角互余.
判定:有一个角是直角的三角形是直角三角形.
(1)直角三角形的两个锐角有怎样的关系?为什么?
(2)如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
(1)根据三角形的内角和定理,即可得到“直角三角形的两锐角互余”.
(2)如图,在△ABC中,∠A+∠B=90°,那么△ABC是直角三角形吗?
在△ABC中,因为∠A+∠B+∠C=180°,又∠A+∠B=90°,所以∠C=90°.于是△ABC是直角三角形.
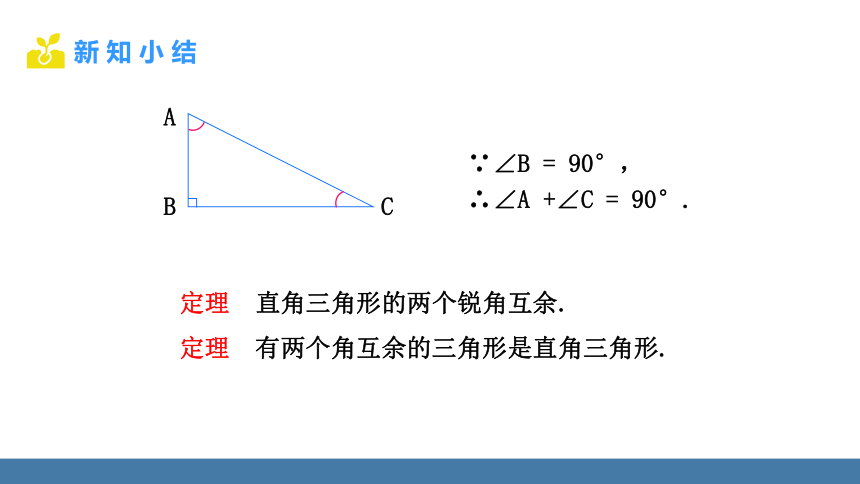
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
A
B
C
∵∠B = 90°,
∴∠A +∠C = 90°.
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
即a2+b2=c2.
a
c
b
勾
弦
股
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的方法得出“这个三角形是直角三角形”的结论.你能证明此结论吗?
已知:如图 ,在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
A
B
C
证明:如图,作 Rt△A′B′C′,使
A′
B′
C′
∠A′=90°,A′B′=AB,A′C′=AC,
则 A′B′2+A′C′2 =B′C′2(勾股定理).
∵AB2+AC2=BC2,
∴BC2=B′C′2.
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
∴∠A=∠A′= 90°(全等三角形的对应角相等).
因此,△ABC是直角三角形.
A
B
C
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
上面两个定理的条件和结论有什么样的关系?
一个命题的条件和结论分别是另一个命题的结论和条件.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
再观察下面三组命题:
1.如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
2.如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
3.一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
观察上面三组命题,你发现了什么
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题.其中一个命题称为另一个命题的逆命题。
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题.
上面每两个命题的条件和结论恰好互换了位置.
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗?
逆命题:如果两个有理数的平方相等,那么这两个有理数相等.
原命题是真命题,逆命题是假命题.
归纳 一个命题是真命题,它的逆命题不一定是真命题.如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
1.下列命题中,属于假命题的是( )
A.三角形三个内角的和等于180°
B.两直线平行,同位角相等
C.矩形的对角线相等
D.相等的角是对顶角
D
2.如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm
C.6 cm D.10 cm
A
B
C
D
E
B
1.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为 ( )
A. 米 B. 米
C.( +1)米 D.3 米
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,,
C.6,7,8 D.2,3,4
B
C
3.如图,在Rt△ABC中,∠C=90°,点D,E分别在AB,AC上,∠B=∠1.求证:△ADE是直角三角形.
证明:在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°.
∵∠B=∠1,
∴∠A+∠1=90°.
∴△ADE是直角三角形.
性质
直角三角形的性质与判定
①直角三角形的两个锐角互余.
②直角三角形两条直角边的平方和等于斜边的平方.
①有两个角互余的三角形是直角三角形;
②三角形两边的平方和等于第三边的平方
判定
命题
原命题、逆命题、互逆命题、真命题、假命题、逆定理
1.2 直角三角形
第1课时 直角三角形的性质与判定
1. 复习直角三角形的相关知识,归纳并掌握直角三角形的性质和判定;(重点)
2. 学习并掌握勾股定理及其逆定理,能够运用其解决问题.(难点)
直角三角形的两个锐角互余.
问题1 直角三角形的定义是什么?
问题2 三角形内角和的性质是什么?
有一个是直角的三角形叫直角三角形.
三角形内角和等于180°.
这节课我们一起来证明直角三角形的判定与性质.
问题3 前面我们探究过直角三角形的哪些性质?
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
我们学过直角三角形的哪些性质和判定方法?与同伴交流.
A
B
C
性质:直角三角形有一个角是直角,两个锐角互余.
判定:有一个角是直角的三角形是直角三角形.
(1)直角三角形的两个锐角有怎样的关系?为什么?
(2)如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
(1)根据三角形的内角和定理,即可得到“直角三角形的两锐角互余”.
(2)如图,在△ABC中,∠A+∠B=90°,那么△ABC是直角三角形吗?
在△ABC中,因为∠A+∠B+∠C=180°,又∠A+∠B=90°,所以∠C=90°.于是△ABC是直角三角形.
定理 直角三角形的两个锐角互余.
定理 有两个角互余的三角形是直角三角形.
A
B
C
∵∠B = 90°,
∴∠A +∠C = 90°.
勾股定理:直角三角形两条直角边的平方和等于斜边的平方.
即a2+b2=c2.
a
c
b
勾
弦
股
反过来,在一个三角形中,当两边的平方和等于第三边的平方时,我们曾用度量的方法得出“这个三角形是直角三角形”的结论.你能证明此结论吗?
已知:如图 ,在△ABC中,AB2+AC2=BC2.
求证:△ABC是直角三角形.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
A
B
C
证明:如图,作 Rt△A′B′C′,使
A′
B′
C′
∠A′=90°,A′B′=AB,A′C′=AC,
则 A′B′2+A′C′2 =B′C′2(勾股定理).
∵AB2+AC2=BC2,
∴BC2=B′C′2.
∴BC=B′C′.
∴△ABC≌△A′B′C′(SSS).
∴∠A=∠A′= 90°(全等三角形的对应角相等).
因此,△ABC是直角三角形.
A
B
C
定理 如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
上面两个定理的条件和结论有什么样的关系?
一个命题的条件和结论分别是另一个命题的结论和条件.
勾股定理 直角三角形两条直角边的平方和等于斜边的平方.
再观察下面三组命题:
1.如果两个角是对顶角,那么它们相等;
如果两个角相等,那么它们是对顶角.
2.如果小明患了肺炎,那么他一定会发烧;
如果小明发烧,那么他一定患了肺炎.
3.一个三角形中相等的边所对的角相等;
一个三角形中相等的角所对的边相等.
观察上面三组命题,你发现了什么
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题.其中一个命题称为另一个命题的逆命题。
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题.
上面每两个命题的条件和结论恰好互换了位置.
你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗?
逆命题:如果两个有理数的平方相等,那么这两个有理数相等.
原命题是真命题,逆命题是假命题.
归纳 一个命题是真命题,它的逆命题不一定是真命题.如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理.
1.下列命题中,属于假命题的是( )
A.三角形三个内角的和等于180°
B.两直线平行,同位角相等
C.矩形的对角线相等
D.相等的角是对顶角
D
2.如图是一张直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm
C.6 cm D.10 cm
A
B
C
D
E
B
1.如图所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为 ( )
A. 米 B. 米
C.( +1)米 D.3 米
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,,
C.6,7,8 D.2,3,4
B
C
3.如图,在Rt△ABC中,∠C=90°,点D,E分别在AB,AC上,∠B=∠1.求证:△ADE是直角三角形.
证明:在Rt△ABC中,∠C=90°,
∴∠A+∠B=90°.
∵∠B=∠1,
∴∠A+∠1=90°.
∴△ADE是直角三角形.
性质
直角三角形的性质与判定
①直角三角形的两个锐角互余.
②直角三角形两条直角边的平方和等于斜边的平方.
①有两个角互余的三角形是直角三角形;
②三角形两边的平方和等于第三边的平方
判定
命题
原命题、逆命题、互逆命题、真命题、假命题、逆定理
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
