浙教版2024年九年级上数学期末模拟卷(含答案)
文档属性
| 名称 | 浙教版2024年九年级上数学期末模拟卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-18 07:13:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版2024年九年级(上)期末模拟卷(含答案)
数学
一、选择题(本题有10小题,每小题3分,共30分)
1.下列事件中,属于必然事件的是( )
A.小明买彩票中奖 B.三角形任意两边之和大于第三边
C.任意抛掷一只纸杯,杯口朝下 D.在一个只有红球的盒子里摸球,摸到了白球
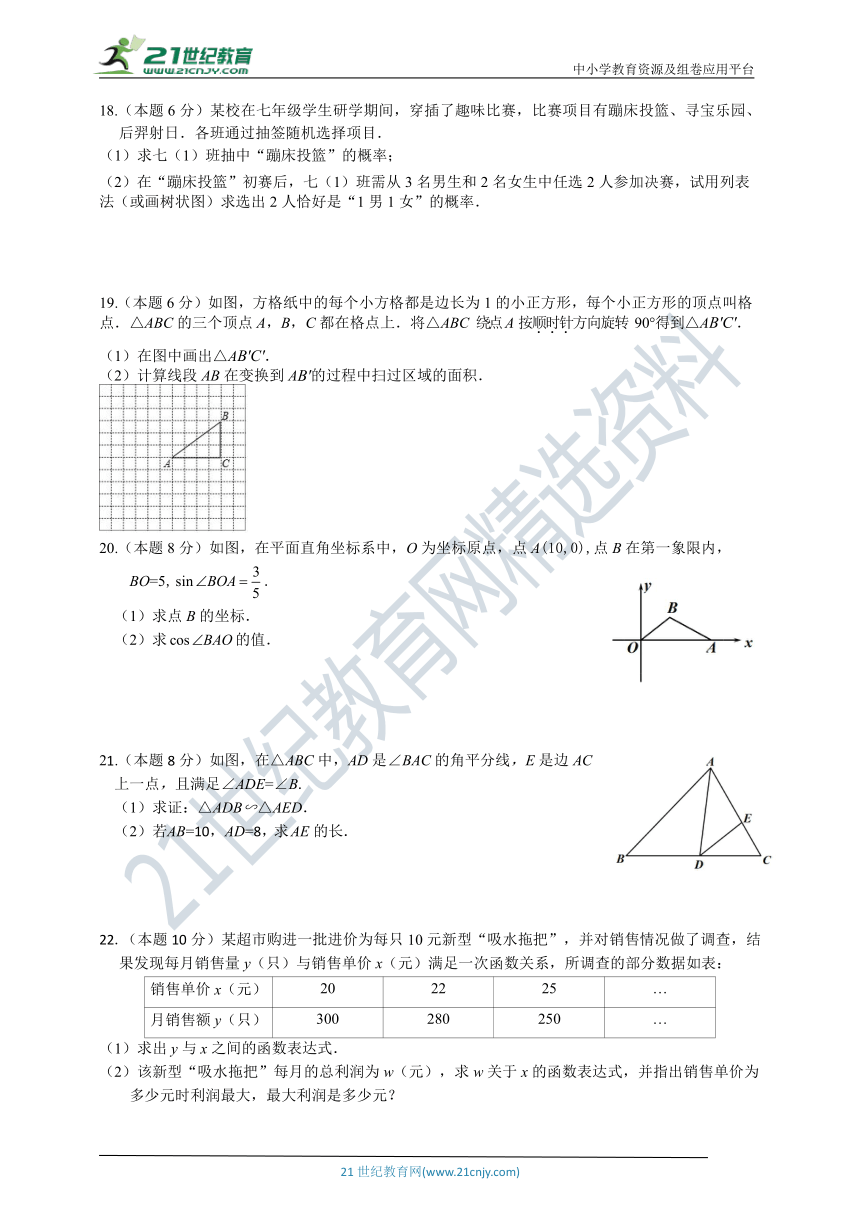
2.已知a,b满足,则的值为( )
A. B. C. D.
3.四边形 ABCD内接于⊙O,∠A=55°,则∠C的度数是( )
A.35° B.55° C.125° D.135°
4.如图,测得一商场自动扶梯的长l为10米,h(米)表示该自动扶梯到达的高度,已知,则h为( )
A.6米 B.7.5米 C.8米 D.12.5米
第4题图 第5题图 第7题图 第8题图 第9题图
5.如图,点A,B,C都在⊙O上,若∠C=34°,则∠AOB的度数为( )
A. 34° B. 56° C. 60° D. 68°
6.抛物线y=3x2先向左平移1个单位,再向上平移1个单位,所得的抛物线是( )
A. B.
C. D.
7.如图 ,若P为△ABC的边AB上一点(AB>AC),则下列条件不能保证△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C. D.
8.如图,在△ABC中,D为AB边上一点,E为AC边上一点,DE//BC,且,若△ADE的面积为4,则四边形BDEC的面积为( )
A.2 B.5 C.6 D.9
9.如图,矩形中,,,点是边上的一个动点(点不与点,重合),现将沿直线折叠,使点落到点处;作的角平分线交于点.设,,则下列图象中,能表示与的函数关系的图象大致是
A. B. C.D.
10.在平面直角坐标系中,正方形ABCD的位置如图所示,点A(1,0),
点D(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1
交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,则正方形
A2024B2024C2024C2023的面积为( )
A. B.
C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.sin30°= .
12.一名职业篮球球员某次投篮训练结果记录如图所示,由此可估计这名球员投篮800次,投中的次数约为 .
第12题图 第13题图 第14题图 第15题图
13.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,以点 B 为圆心,BC长为半径画弧,交边 AB 于点 D,则的长为 .
14.生活中到处可见黄金分割的美.如图,在设计人物雕像时,使雕像腰部以下a与全身高度b的比值等于黄金比,可以增加视觉美感.若图中b为2米,则a为 米.(精确到0.1米)
15.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=2,则AD为 .
16.已知A,B的坐标分别为(1,0)和(2,0),若二次函数的图象与线段AB只有一个交点,则a的取值范围是 .
三、解答题(本题有8小题,共66分,请写出必要的解答过程)
17.(本题6分)下面计算错在哪里?指出错误步骤的序号,并给出正确的解答步骤.
(1)错误步骤: .(填最先出错的步骤序号即可)
(2)写出正确的解答步骤.
18.(本题6分)某校在七年级学生研学期间,穿插了趣味比赛,比赛项目有蹦床投篮、寻宝乐园、后羿射日.各班通过抽签随机选择项目.
(1)求七(1)班抽中“蹦床投篮”的概率;
(2)在“蹦床投篮”初赛后,七(1)班需从3名男生和2名女生中任选2人参加决赛,试用列表法(或画树状图)求选出2人恰好是“1男1女”的概率.
19.(本题6分)如图,方格纸中的每个小方格都是边长为1的小正方形,每个小正方形的顶点叫格点.△ABC的三个顶点A,B,C都在格点上.将△ABC 绕点 A按顺时针方向旋转 90°得到△AB′C′.
(1)在图中画出△AB′C′.
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
20.(本题8分)如图,在平面直角坐标系中,O为坐标原点,点A(10,0),点B在第一象限内,
BO=5,.
(1)求点B的坐标.
(2)求的值.
21.(本题8分)如图,在△ABC中,AD是∠BAC的角平分线,E是边AC上一点,且满足∠ADE=∠B.
(1)求证:△ADB∽△AED.
(2)若 AB=10,AD=8,求 AE的长.
22.(本题10分)某超市购进一批进价为每只10元新型“吸水拖把”,并对销售情况做了调查,结果发现每月销售量y(只)与销售单价x(元)满足一次函数关系,所调查的部分数据如表:
销售单价x(元) 20 22 25 …
月销售额y(只) 300 280 250 …
(1)求出y与x之间的函数表达式.
(2)该新型“吸水拖把”每月的总利润为w(元),求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
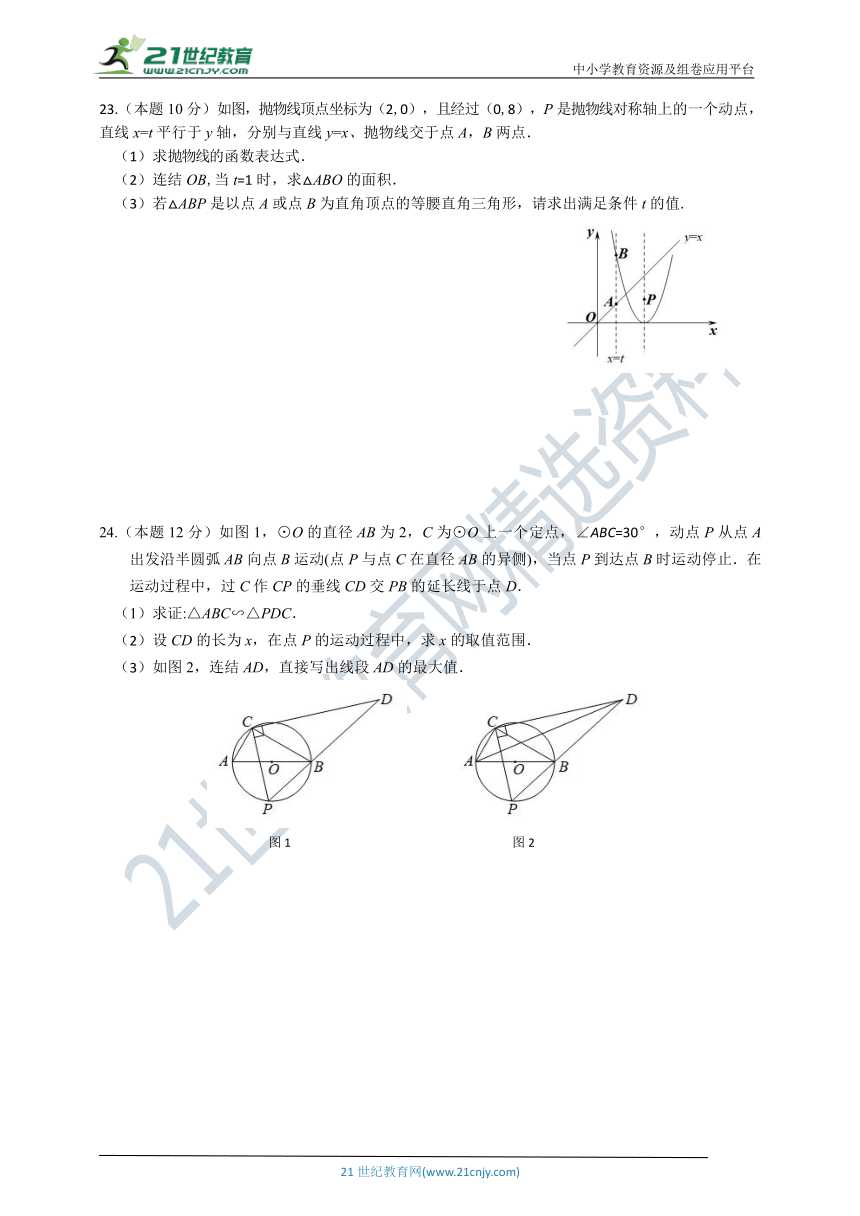
23.(本题10分)如图,抛物线顶点坐标为(2,0),且经过(0,8),P是抛物线对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线交于点A,B两点.
(1)求抛物线的函数表达式.
(2)连结OB,当t=1时,求△ABO的面积.
(3)若△ABP是以点A或点B为直角顶点的等腰直角三角形,请求出满足条件t的值.
24.(本题12分)如图1,⊙O的直径AB为2,C为⊙O上一个定点,∠ABC=30°,动点P从点A出发沿半圆弧AB向点B运动(点P与点C在直径AB的异侧),当点P到达点B时运动停止.在运动过程中,过C作CP的垂线CD交PB的延长线于点D.
(1)求证:△ABC∽△PDC.
(2)设CD的长为x,在点P的运动过程中,求x的取值范围.
(3)如图2,连结AD,直接写出线段AD的最大值.
图1 图2
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1-5 BBCAD 6-10 CCBDD
二.填空题(共6小题,满分18分,每小题3分)
11.0.5
12.600
13.
14.1.2
15.12
16.或-1≤a<-0.5
三.解答题(共8小题,满分72分)
17.(1)① (2)
18.解:(1)七(1)班抽中“蹦床投篮”的概率是;
(2)根据题意画图如下:
共有20种等可能的结果,选出2人恰好是“1男1女”的有12种,
则选出2人恰好是“1男1女”的概率是.
19.(1)如图所示,△AB'C'即为所求;
(2)因为AB5,
所以线段AB在旋转过程中所扫过的面积为π.
20.解:(1)过点B作BD⊥OA,垂足为D.
∵sin∠BOA,BO=5,
∴BD=3.
∴OD4.
∴点B的坐标为(4,3);
(2)∵AO=OD+AD=10,OD=4,
∴AD=6.
∴AB3.
∴cos∠BAO.
21.(1)证明:在△ABC中,AD是∠BAC的平分线,点E是边AC上一点,且满足∠ADE=∠B.
∴∠BAD=∠DAE,
∴△ADB∽△AED;
(2)解:∵△ADB∽△AED,
∴,
∵AB=10,AD=8,
∴,
∴.
22.解:(1)设y=kx+b(k≠0),
根据题意代入点(20,300),(25,250),
∴
解得,
∴y=﹣10x+500.
(2)依题意得,w=(x﹣10)(﹣10x+500)=﹣10x2+600x﹣5000=﹣10(x﹣30)2+4000,
∵a=﹣10<0,
∴当x=30时,w有最大值4000,
即当销售单价定为30元时,每月可获得最大利润4000元.
23.解:(1)
(2)
(3)y=2(x﹣2)2=2x2﹣8x+8,
∴抛物线的对称轴为直线x=2,
∵直线x=t与直线y=x、抛物线交于点A、B,
∴点A的坐标为(t,t),点B的坐标为(t,2t2﹣8t+8),
∴AB=|2t2﹣8t+8﹣t|=|2t2﹣9t+8|,
AP=|t﹣2|,
∵△APB是以点A或B为直角顶点的三角形,
∴|2t2﹣9t+8|=|t﹣2|,
∴2t2﹣9t+8=t﹣2①或2t2﹣9t+8=﹣(t﹣2)②,
整理①得,t2﹣5t+5=0,
解得t1,t2,
整理②得,t2﹣4t+3=0,
解得t1=1,t2=3,
综上所述,满足条件的t值为:1或3或或.
故答案为:1或3或或.
24.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥CP,
∴∠PCD=90°,
∴∠ACB=∠PCD,
∵∠ABC=30°,
∴∠A=60°,
∵,
∴∠A=∠P,
∴△ABC∽△PDC;
(2)解:在Rt△ABC中,∠ABC=30°,AB=2,
∴ACAB=1,
由(1)知:∠P=∠A=60°,
∴∠D=∠ABC=30°,
∴tanD=tan30°,
∵CD的长为x,
∴PCx,
∵动点P从A点出发沿半圆弧AB向B点运动,
∴1≤PC≤2,
∴1x≤2,
∴x≤2;
(3)由(1)知:△ABC∽△PDC,
∴∠PDC=∠ABC=30°,即∠BDC=30°,
∴点D在以BC为弦,所含圆周角为30°的优弧上运动,作△BCD的外接圆⊙O′,连接AO′并延长交⊙O′于点D′,
则AD′为线段AD的最大值,
如图,连接O′B,O′C,
则∠BO′C=2∠BDC=60°,O′B=O′C,
∴△O′BC是等边三角形,
∴O′D′=O′B=BC,∠O′BC=60°,
∴∠ABO′=∠ABC+∠O′BC=30°+60°=90°,
∴O′A,
∴AD′=O′A+O′D′;
∴线段AD的最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙教版2024年九年级(上)期末模拟卷(含答案)
数学
一、选择题(本题有10小题,每小题3分,共30分)
1.下列事件中,属于必然事件的是( )
A.小明买彩票中奖 B.三角形任意两边之和大于第三边
C.任意抛掷一只纸杯,杯口朝下 D.在一个只有红球的盒子里摸球,摸到了白球
2.已知a,b满足,则的值为( )
A. B. C. D.
3.四边形 ABCD内接于⊙O,∠A=55°,则∠C的度数是( )
A.35° B.55° C.125° D.135°
4.如图,测得一商场自动扶梯的长l为10米,h(米)表示该自动扶梯到达的高度,已知,则h为( )
A.6米 B.7.5米 C.8米 D.12.5米
第4题图 第5题图 第7题图 第8题图 第9题图
5.如图,点A,B,C都在⊙O上,若∠C=34°,则∠AOB的度数为( )
A. 34° B. 56° C. 60° D. 68°
6.抛物线y=3x2先向左平移1个单位,再向上平移1个单位,所得的抛物线是( )
A. B.
C. D.
7.如图 ,若P为△ABC的边AB上一点(AB>AC),则下列条件不能保证△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C. D.
8.如图,在△ABC中,D为AB边上一点,E为AC边上一点,DE//BC,且,若△ADE的面积为4,则四边形BDEC的面积为( )
A.2 B.5 C.6 D.9
9.如图,矩形中,,,点是边上的一个动点(点不与点,重合),现将沿直线折叠,使点落到点处;作的角平分线交于点.设,,则下列图象中,能表示与的函数关系的图象大致是
A. B. C.D.
10.在平面直角坐标系中,正方形ABCD的位置如图所示,点A(1,0),
点D(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1
交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,则正方形
A2024B2024C2024C2023的面积为( )
A. B.
C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.sin30°= .
12.一名职业篮球球员某次投篮训练结果记录如图所示,由此可估计这名球员投篮800次,投中的次数约为 .
第12题图 第13题图 第14题图 第15题图
13.如图,在△ABC中,∠ACB=90°,∠A=30°,AB=4,以点 B 为圆心,BC长为半径画弧,交边 AB 于点 D,则的长为 .
14.生活中到处可见黄金分割的美.如图,在设计人物雕像时,使雕像腰部以下a与全身高度b的比值等于黄金比,可以增加视觉美感.若图中b为2米,则a为 米.(精确到0.1米)
15.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=2,则AD为 .
16.已知A,B的坐标分别为(1,0)和(2,0),若二次函数的图象与线段AB只有一个交点,则a的取值范围是 .
三、解答题(本题有8小题,共66分,请写出必要的解答过程)
17.(本题6分)下面计算错在哪里?指出错误步骤的序号,并给出正确的解答步骤.
(1)错误步骤: .(填最先出错的步骤序号即可)
(2)写出正确的解答步骤.
18.(本题6分)某校在七年级学生研学期间,穿插了趣味比赛,比赛项目有蹦床投篮、寻宝乐园、后羿射日.各班通过抽签随机选择项目.
(1)求七(1)班抽中“蹦床投篮”的概率;
(2)在“蹦床投篮”初赛后,七(1)班需从3名男生和2名女生中任选2人参加决赛,试用列表法(或画树状图)求选出2人恰好是“1男1女”的概率.
19.(本题6分)如图,方格纸中的每个小方格都是边长为1的小正方形,每个小正方形的顶点叫格点.△ABC的三个顶点A,B,C都在格点上.将△ABC 绕点 A按顺时针方向旋转 90°得到△AB′C′.
(1)在图中画出△AB′C′.
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
20.(本题8分)如图,在平面直角坐标系中,O为坐标原点,点A(10,0),点B在第一象限内,
BO=5,.
(1)求点B的坐标.
(2)求的值.
21.(本题8分)如图,在△ABC中,AD是∠BAC的角平分线,E是边AC上一点,且满足∠ADE=∠B.
(1)求证:△ADB∽△AED.
(2)若 AB=10,AD=8,求 AE的长.
22.(本题10分)某超市购进一批进价为每只10元新型“吸水拖把”,并对销售情况做了调查,结果发现每月销售量y(只)与销售单价x(元)满足一次函数关系,所调查的部分数据如表:
销售单价x(元) 20 22 25 …
月销售额y(只) 300 280 250 …
(1)求出y与x之间的函数表达式.
(2)该新型“吸水拖把”每月的总利润为w(元),求w关于x的函数表达式,并指出销售单价为多少元时利润最大,最大利润是多少元?
23.(本题10分)如图,抛物线顶点坐标为(2,0),且经过(0,8),P是抛物线对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线交于点A,B两点.
(1)求抛物线的函数表达式.
(2)连结OB,当t=1时,求△ABO的面积.
(3)若△ABP是以点A或点B为直角顶点的等腰直角三角形,请求出满足条件t的值.
24.(本题12分)如图1,⊙O的直径AB为2,C为⊙O上一个定点,∠ABC=30°,动点P从点A出发沿半圆弧AB向点B运动(点P与点C在直径AB的异侧),当点P到达点B时运动停止.在运动过程中,过C作CP的垂线CD交PB的延长线于点D.
(1)求证:△ABC∽△PDC.
(2)设CD的长为x,在点P的运动过程中,求x的取值范围.
(3)如图2,连结AD,直接写出线段AD的最大值.
图1 图2
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1-5 BBCAD 6-10 CCBDD
二.填空题(共6小题,满分18分,每小题3分)
11.0.5
12.600
13.
14.1.2
15.12
16.或-1≤a<-0.5
三.解答题(共8小题,满分72分)
17.(1)① (2)
18.解:(1)七(1)班抽中“蹦床投篮”的概率是;
(2)根据题意画图如下:
共有20种等可能的结果,选出2人恰好是“1男1女”的有12种,
则选出2人恰好是“1男1女”的概率是.
19.(1)如图所示,△AB'C'即为所求;
(2)因为AB5,
所以线段AB在旋转过程中所扫过的面积为π.
20.解:(1)过点B作BD⊥OA,垂足为D.
∵sin∠BOA,BO=5,
∴BD=3.
∴OD4.
∴点B的坐标为(4,3);
(2)∵AO=OD+AD=10,OD=4,
∴AD=6.
∴AB3.
∴cos∠BAO.
21.(1)证明:在△ABC中,AD是∠BAC的平分线,点E是边AC上一点,且满足∠ADE=∠B.
∴∠BAD=∠DAE,
∴△ADB∽△AED;
(2)解:∵△ADB∽△AED,
∴,
∵AB=10,AD=8,
∴,
∴.
22.解:(1)设y=kx+b(k≠0),
根据题意代入点(20,300),(25,250),
∴
解得,
∴y=﹣10x+500.
(2)依题意得,w=(x﹣10)(﹣10x+500)=﹣10x2+600x﹣5000=﹣10(x﹣30)2+4000,
∵a=﹣10<0,
∴当x=30时,w有最大值4000,
即当销售单价定为30元时,每月可获得最大利润4000元.
23.解:(1)
(2)
(3)y=2(x﹣2)2=2x2﹣8x+8,
∴抛物线的对称轴为直线x=2,
∵直线x=t与直线y=x、抛物线交于点A、B,
∴点A的坐标为(t,t),点B的坐标为(t,2t2﹣8t+8),
∴AB=|2t2﹣8t+8﹣t|=|2t2﹣9t+8|,
AP=|t﹣2|,
∵△APB是以点A或B为直角顶点的三角形,
∴|2t2﹣9t+8|=|t﹣2|,
∴2t2﹣9t+8=t﹣2①或2t2﹣9t+8=﹣(t﹣2)②,
整理①得,t2﹣5t+5=0,
解得t1,t2,
整理②得,t2﹣4t+3=0,
解得t1=1,t2=3,
综上所述,满足条件的t值为:1或3或或.
故答案为:1或3或或.
24.(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD⊥CP,
∴∠PCD=90°,
∴∠ACB=∠PCD,
∵∠ABC=30°,
∴∠A=60°,
∵,
∴∠A=∠P,
∴△ABC∽△PDC;
(2)解:在Rt△ABC中,∠ABC=30°,AB=2,
∴ACAB=1,
由(1)知:∠P=∠A=60°,
∴∠D=∠ABC=30°,
∴tanD=tan30°,
∵CD的长为x,
∴PCx,
∵动点P从A点出发沿半圆弧AB向B点运动,
∴1≤PC≤2,
∴1x≤2,
∴x≤2;
(3)由(1)知:△ABC∽△PDC,
∴∠PDC=∠ABC=30°,即∠BDC=30°,
∴点D在以BC为弦,所含圆周角为30°的优弧上运动,作△BCD的外接圆⊙O′,连接AO′并延长交⊙O′于点D′,
则AD′为线段AD的最大值,
如图,连接O′B,O′C,
则∠BO′C=2∠BDC=60°,O′B=O′C,
∴△O′BC是等边三角形,
∴O′D′=O′B=BC,∠O′BC=60°,
∴∠ABO′=∠ABC+∠O′BC=30°+60°=90°,
∴O′A,
∴AD′=O′A+O′D′;
∴线段AD的最大值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
