6.3.2二项式系数的性质(更新版) 课件(共17张PPT)
文档属性
| 名称 | 6.3.2二项式系数的性质(更新版) 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 21:52:17 | ||
图片预览





文档简介
(共17张PPT)
人教A版(2019)选修第三册
第 六 章 计数原理
6.3.2 二项式系数的性质
n (a+b)n展开式的二项式系数 (a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
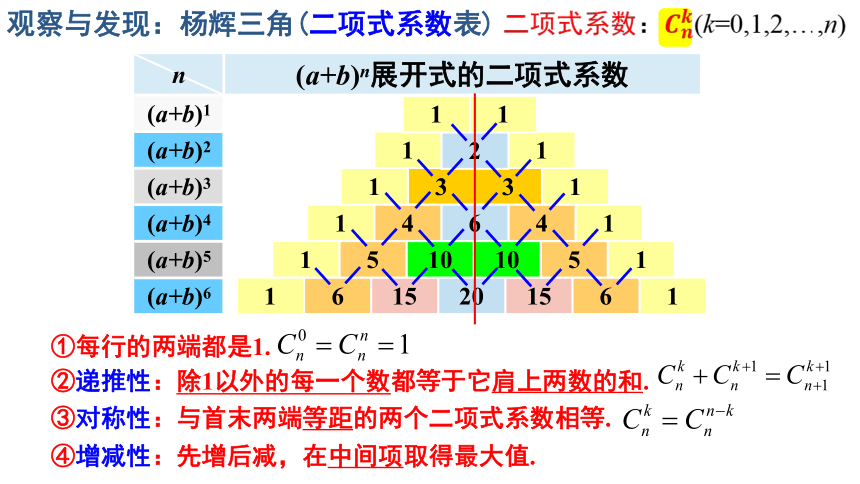
观察与发现:杨辉三角(二项式系数表)
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
二项式系数:(k=0,1,2,…,n)
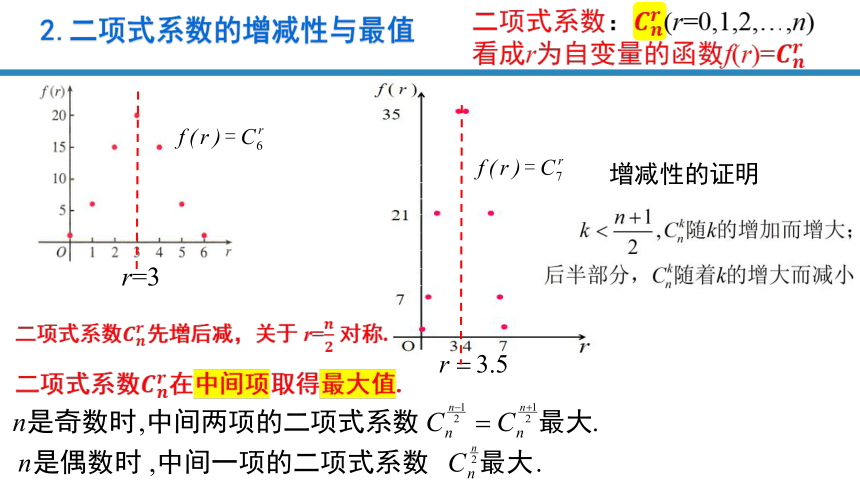
2.二项式系数的增减性与最值
二项式系数:(r=0,1,2,…,n)
看成r为自变量的函数f(r)=
r=3
增减性的证明
二项式系数先增后减,关于 r= 对称.
二项式系数在中间项取得最大值.
3.数列的分类
递增数列:从第2项起,每一项都大于它的前一项的数列.
递减数列:从第2项起,每一项都小于它的前一项的数列.
摆动数列: 从第2项起,有些项大于它的前一项,有些项小于 它的前一项的
数列.
常数列:各项相等的数列.
(1) 按项的变化趋势分:
(2) 按项的个数分:
有穷数列:个数有限的的数列
无穷数列:个数无限的的数列
对任意n∈N*,总有an+1>an (或an+1-an>0).
对任意n∈N*,总有an+1第8项为中间项
共15项
14
8
4和5
11
6
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
2.二项式系数的增减性与最值
关于k= 对称.
3.各二项式系数的和
只与n有关,与a,b无关.
3.各二项式系数的和
[练习2 - 2]一串装饰彩灯由灯泡串联而成,每串有20个灯泡,只要有一个灯泡坏了,整串灯泡就不亮,则因灯泡损坏致使一串彩灯不亮的可能性的种数为( )
A.20 B.219 C.220 D.220-1
D
二项式系数性质的应用
赋值法:
系数和问题
X
Y
系数最大:正系数中的最大
系数最小:负系数中的最小
系数绝对值最大
共性
二项式系数性质的应用
小结:系数的求和与最值问题
1.二项式系数和:
2.奇/偶数项的二项式系数和:
3.各项系数和X+Y:
4.奇数项的系数和X:
5.系数ak(ak为正)的最大值:
6.系数|ak|(ak正负交替)的最大值:
7.系数ak(ak正负交替)的最大/小值:
8.系数a0:
二项式系数性质当堂训练
二项式系数性质当堂训练
二项式系数性质当堂训练
二项式系数性质当堂训练
二项式系数性质当堂训练
5
二项式系数性质当堂训练
二项式系数性质当堂训练
人教A版(2019)选修第三册
第 六 章 计数原理
6.3.2 二项式系数的性质
n (a+b)n展开式的二项式系数 (a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
观察与发现:杨辉三角(二项式系数表)
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
二项式系数:(k=0,1,2,…,n)
2.二项式系数的增减性与最值
二项式系数:(r=0,1,2,…,n)
看成r为自变量的函数f(r)=
r=3
增减性的证明
二项式系数先增后减,关于 r= 对称.
二项式系数在中间项取得最大值.
3.数列的分类
递增数列:从第2项起,每一项都大于它的前一项的数列.
递减数列:从第2项起,每一项都小于它的前一项的数列.
摆动数列: 从第2项起,有些项大于它的前一项,有些项小于 它的前一项的
数列.
常数列:各项相等的数列.
(1) 按项的变化趋势分:
(2) 按项的个数分:
有穷数列:个数有限的的数列
无穷数列:个数无限的的数列
对任意n∈N*,总有an+1>an (或an+1-an>0).
对任意n∈N*,总有an+1
共15项
14
8
4和5
11
6
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
2.二项式系数的增减性与最值
关于k= 对称.
3.各二项式系数的和
只与n有关,与a,b无关.
3.各二项式系数的和
[练习2 - 2]一串装饰彩灯由灯泡串联而成,每串有20个灯泡,只要有一个灯泡坏了,整串灯泡就不亮,则因灯泡损坏致使一串彩灯不亮的可能性的种数为( )
A.20 B.219 C.220 D.220-1
D
二项式系数性质的应用
赋值法:
系数和问题
X
Y
系数最大:正系数中的最大
系数最小:负系数中的最小
系数绝对值最大
共性
二项式系数性质的应用
小结:系数的求和与最值问题
1.二项式系数和:
2.奇/偶数项的二项式系数和:
3.各项系数和X+Y:
4.奇数项的系数和X:
5.系数ak(ak为正)的最大值:
6.系数|ak|(ak正负交替)的最大值:
7.系数ak(ak正负交替)的最大/小值:
8.系数a0:
二项式系数性质当堂训练
二项式系数性质当堂训练
二项式系数性质当堂训练
二项式系数性质当堂训练
二项式系数性质当堂训练
5
二项式系数性质当堂训练
二项式系数性质当堂训练
